基于SoC FPGA异构平台的魔方快速还原系统设计与实现

(湖北大学 物理与电子科学学院，武汉 430062)

0 引言

随着科技的发展，各种自动化作业平台在各行各业发挥着越来越重要的作用。我国对自动化智能平台相关技术的研究投入也非常巨大。本文所研究的快速魔方还原系统正是自动化智能平台的一个典型应用场景。

该快速魔方还原系统基于SoC FPGA异构平台实现。其中SoC采用的是ARM处理器，它作为SoC中的佼佼者，兼顾性能、功耗、代码密度、价格等多个方面，且第三方支持非常全面。而FPGA则以其设计灵活性和高并行著称。在将FPGA和ARM核相结合后，可以实现非常高效的设计。本文快速魔方还原系统采用的硬件平台是台湾友晶公司提供的SoC FPGA异构DE1-SoC开发板。该板卡提供了一个以Intelcyclone VSoC FPGA芯片建立的强大的硬件设计平台，结合了嵌入式双核Cortex-A9和业界领先的FPGA可编程逻辑。同时还包括了诸如高速DDR3内存、ADC、以太网络等丰富的功能外设。足以满足快速魔方还原系统设计的需求，兼具高性能和低功耗[1]。

1 系统设计

整个魔方还原系统由开发板、CCD摄像头、魔方还原机械结构以及VGA显示器组成。开发板控制部分基于Intel SoC FPGA异构框架，FPGA端和HPS端各自发挥所长[2]，分工协作，具体框图如图1所示。

图1 系统框图

在HPS端，分为以下4个步骤：

第1步，控制FPGA部分的图像处理模块和舵机转动模块，依次获取魔方6个面的色块中心区域的RGB均值。

第2步，调用颜色识别算法对魔方每个色块的颜色进行判断，得出初始魔方。

第3步，调用魔方还原二阶段算法，得出30步阈值以内的魔方还原步骤。

第4步，将还原步骤转换并编码后，发送给FPGA端舵机转动模块。

在FPGA端，主要分为4个模块：CCD摄像头图像采集模块，图像处理模块，VGA显示模块，舵机控制模块。

1.1 CCD图像采集模块

CCD摄像头与CMOS摄像头相比，在不管是强光还是弱光的不利条件下，图像画质都要更高[3]。CCD摄像头输入的是模拟信号，需要经过一系列的处理最终转换成RGB图像，整个图像采集的过程如图2所示。

图2 图像采集框图

CCD摄像头输入的影像信号送至开发板上的电视译码芯片(ADV7180)，译码之后得到8 位 ITU_R BT.656标准接口的影像数据，然后送入FPGA芯片。在FPGA内，先由ITU-R 656 译码模块将亮度与彩度信号分解，再送入De-interlace模块完成解交错处理，接着送入Scaler模块完成缩放处理，得到YCbCr格式的图像数据，然后进入YCbCr2RGB模块，转换成 RGB值数据，再根据640*480像素VGA显示需要的timing，将数字的RGB信号送出FPGA芯片，进入开发板上的DA转换芯片(ADV7123)，最终输出三路模拟RGB信号到VGA显示器。这样，摄像头拍摄到的画面就实时显示在了VGA显示器上了。

1.2 图像处理模块

图像采集模块输出的是一帧帧分辨率为 640*480 的 RGB 图像，在此图像处理模块中，要做的处理分为三步，首先是要把一帧画面中，魔方表面9个色块的中心部分10*10 个像素点的RGB值存储到 RAM 中[4]；然后从 RAM 中依次读出每个色块中心区域读出 RGB 数据，求得R均值、G均值、B均值；最后将9组RGB值及当前魔方面一起编码后，传送到 HPS端。

1.3 VGA显示模块

本设计采用VGA显示器作为显示终端，显示的内容分为两部分，在VGA的左侧，呈现的是CCD摄像头实时获取的画面，右侧则是绘制的魔方的展开平铺图。HPS端颜色识别的结果会显示在魔方平铺图内，用于人眼直观判断识别结果。此外，通过读取ROM中存放的数据,将湖北大学logo也显示在里屏幕上，具体显示效果如图3所示。

图3 VGA显示方式

1.4 舵机控制模块

本设计使用的魔方还原机械结构主要由4个机械臂组成，若要机械臂稳定快速的完成魔方面的旋转，对总计8个舵机的同步控制尤为重要。本模块的功能就是接收动作编码，通过8个GPIO 端口，同步控制8个舵机转动，完成机械手臂的旋转伸缩。

2 FPGA与HPS之间的桥接

在Intel SoC FPGA的设计架构里面，FPGA与HPS之间存在两种通信方式，FPGAto SDRAM和AXIbridge接口。FPGAto SDRAM接口是HPS内部的SDRAM控制器提供给FPGA访问HPS内存的接口。AXIbridge是FPGA和HPS总线间数据交互的接口，包括FPGA-to-HPS AXI、HPS-to-FPGA AXI和Light-weight HPS-to-FPGA AXI。

HPS向FPGA端需要传输的数据有控制指令、魔方还原步骤编码，数据量较小，选用轻量级的HPS-to-FPGA AXI Bridge为传输通路；FPGA向HPS端仅需传输每个面9个色块的中心区域的RGB均值，通过多组PIO传输即可。

3 关键算法

3.1 颜色识别算法

本设计需要做的颜色识别具有两点特殊性：

1)读入的数据是6个面，每个面9个色块，总计54个色块的中心区域100个像素点的R均值、G均值、B均值；

2)每个色块的颜色只可能是红橙黄绿蓝白中的一种。

基于此，我们设计了如下简单高效的颜色识别算法：

1)采集当前环境下，还原后的魔方每个面的每个色块的RGB值，存储每种颜色的9组RGB值；

2)设置一个颜色判定值v=a*R+b*G+c*B，a、b、c初值均为-128，取值范围从-128～128，变化步径设为4。三重循环遍历所有可能的a、b、c值组合，找到最合适的那组a、b、c值。使得某种颜色9个色块的RGB值算得的v值接近，且远大于其余5种颜色的色块的RGB值算得的v值。

3)依据2)得到的6组不同的a、b、c值，计算FPGA端传过来的54组RGB的v值，依次找出每种颜色的9个色块。

3.2 魔方还原算法

3.2.1 魔方的表示方法

采集到魔方状态之后，我们需要用一种方式保存初始魔方状态。魔方有8个脚块，12个棱块，魔方的摆放为：U蓝色，F红色，R黄色，L白色，B橙色，D绿色。本设计中用如下编码存储。

表1 角块编码

表2 棱块编码

对于每一个角块，还需要一个参数来确定：顺时针扭转次数。如图4，对于3个魔方前面右上角的的蓝橙黄角块，处于相同的位置，但是处于不同的扭转状态。若选择顶面的蓝色作为参考色，以顶面中心蓝色块为中心，第一个角块的蓝色块已在顶面；第2个角块可通过顺时针扭转1次，使蓝色块到达顶面；第3个角块可通过顺时针扭转2次，使蓝色块到达顶面。分别用0，1，2表示。

图4 3种不同的蓝橙黄角块

而对于棱块，只有两种可能，翻转或者正常。如图5，两个魔方的前面上方的红蓝棱块。第一个处于正确位置，用0表示，第2个通过翻转之后可到正确位置，用1表示。

图5 2种不同的红蓝棱块

这样，定义一个魔方的数组int MF[3][3][3][2][b][c]([第n行][第n列][第n层][编号或扭转数][第b步][第c次循环])，用于保存魔方的状态。

魔方有6个面，每个面存在3种操作(正对该面，顺时针旋转、逆时针旋转、180度旋转)一共18种操作。本设计采用如下方式的简称：F=front face，前面；B=back face，后面；R=right face，右面；L=left face，左面；U=up face，上面；D=down face，下面。以前面F为例，顺时针旋转90°表示为[F]；逆时针旋转90°表示为[F’]；180度旋转表示为[F2]。后面则相应为[B][B’][B2]，其余面依此类推。

3.2.2 二阶段算法

本设计采用的魔方还原算法，是一种迭代加深启发式的搜索算法(IDA*)。过程规则很简单，没有很复杂的状态判断，就只是重复循环：对每个阶段的魔方不断重复尝试不同的旋转，然后进行判断是否达到目标状态，如果没有，则根据一个估价函数，选择估价最低的操作继续尝试[5]。

因为魔方每一次的旋转都有18种可能，如果每次都做18种尝试，循环次数过于庞大。二阶段算法正式为了解决这一问题，将魔方还原分为两个阶段，在第一阶段需要用所有18种可能去尝试，但是第二阶段只需要用其中一部分可能转法就确定可将魔方还原。

群是一种特殊的集合，对于一种操作，用它作用于一个集合的元素的时候，得到的结果还是这个集合里的元素时，这个集合对于某个操作构成一个群。而魔方的所有状态中就有着这样的特殊集合，群[6]。对于一个未打乱的魔方，如果你使用R2、L2、F2、B2、U、U’、U2、D、D’、D2这10种转法来转动它，能生成的状态仅是魔方所有可能状态群中的一个子群。这个子群表示为 G1 = 。在这个子群中，角块和棱块的扭转是不能被改变的。也就是说，当一个棱块或是角块处在一个特定位置时，它的翻转数和扭转次数是一样的，为0。同时，UD 夹层(U 层和 D 层中间的那一层，即中层 E)上的棱块始终位于该夹层上。

在第一阶段中，用所有18种可能的操作去作用于初始状态，当所有块的翻转数，扭转数为0，且中间棱块都在中间的时候，则到达G1群，第一阶段完成。第二阶段，仅用群的10种可能操作作用于此时状态，直到所有块的位置都正确，则魔方还原。

具体流程如图6所示。

图6 魔方还原算法流程图

通过分析计算，第一阶段最高12步还原，当代价超过12步则舍弃后序操作，尝试另一种操作。第二阶段最高18步还原，当代价超过18步则舍弃后序操作，尝试另一种操作。算法第一次搜索出的结果一般很快，在30步之内，然而，它不会马上停止，而是继续搜索，搜索还没有尝试的操作，如果所有操作都搜索完成，则改变预先的剪枝深度，比如第一阶段为13步，虽然第一阶段会提高步数，但是第二阶段可能会减少许多步数，比如从原来的15步降低到8步，最终步数会进一步减少。当时间达到设定阈值，或者步数达到设定阈值的时候，算法停止工作，并输出结果。

在具体代码实现过程中，用如表3、表4对每一步的操作进行编码。

4 机械结构设计

4.1 关于舵机

舵机由一个步进电机、一个基准电路以及其他的一些部件组成。信号线进来不同的信号时会和基准电路进行比

表3 第一阶段还原步骤编码方式

表4 第二阶段还原步骤编码方式

较，从而来决定舵机的转动方向。通过改变输入脉冲信号的高电平时间即可控制舵机旋转的角度。在一个周期为20 ms的脉冲里面高电平持续的时间决定了舵机转动的角度，对于本设计中使用的180°舵机，对应关系如表5。

表5 高电平脉冲时间和转动度数关系

4.2 魔方还原机械机构

本设计采用的魔方还原机械结构由4个同样的机械手臂，四面对称摆放构成[7]，单个机械手臂的结构如图7所示，一前一后装有2个舵机。一个控制机械爪的伸缩，另一个控制机械爪的旋转。整个魔方还原机械结构的实物图如图8所示。

图7 机械手臂结构图

图8 魔方还原机械结构实物图

4.3 魔方还原动作设计

如第四章所述，魔方还原总计有18种不同的操作，但是我们的机械结构只能做到前后左右面每个面的3种不同翻转，总计12种不同操作。同时，若前后两个动作分别是前面和后面或者左面和右面的操作，这两个动作是可以同时执行的。我们对所有可能的魔方操作进行了如表6、表7、表8所示的编码。

表6 单面旋转方式编码

表7 前后面同时旋转方式编码

表8 左右面同时旋转方式编码

对于机械结构无法做到的U,U’,U2以及D,D’D2这6种操作，需要借助整体转动魔方，转换为可做到的12种操作，因此我们定义了表9中的魔方整体旋转操作：

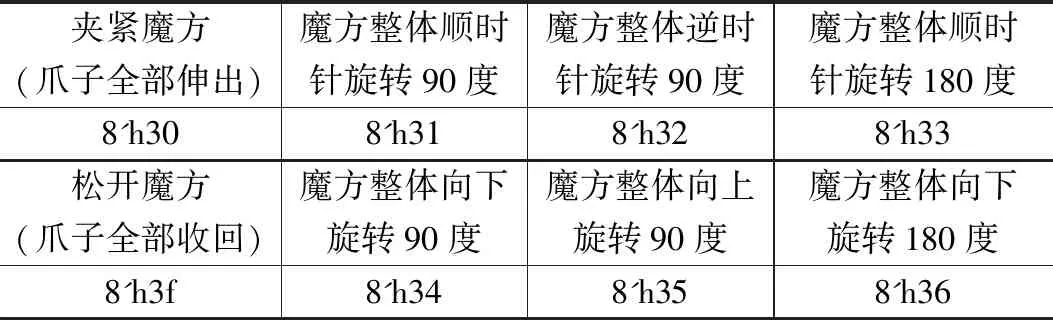
表9 魔方整体旋转编码

5 实验结果与分析

根据上述分析，设计实现了魔方还原系统，如图8所示。系统工作流程为，打开电源，4个方向的机械爪全部收回，置于机械结构顶部的摄像头开始工作；放入魔方，按下开始按键，机械爪首先夹紧魔方，然后整体转动魔方，依次将6个面暴露在摄像头下；摄像头捕获到的画面传入FPGA，一方面提取出色块中心区域RGB均值送入HPS端，另一方面将画面实时显示在VGA显示器上；HPS端执行颜色识别程序，识别得到的完整魔方传入魔方还原程序；还原步骤经编码后送回FPGA端的机械结构控制模块，最终由机械结构完成对打乱魔方的复原；魔方还原完毕后，机械抓全部收回，魔方掉出。

为了验证系统的性能，首先单独测试了关键的颜色识别算法和魔方还原算法，然后对整套系统进行了实际的魔方还原测试，具体测试结果如下。

5.1 颜色识别测试结果

基于系统实际工作的环境不同，而光照对于摄像头图像影响非常大，我们分别在光照良好的白天室内、白光灯良好照明下的晚上室内以及黄光灯良好照明下的晚上3种不同光照条件下，分别任意打乱魔方50次，调用颜色识别算法测试模块检测魔方所有色块的颜色。得到如表10的识别结果。

表10 3种光照条件下的颜色识别测试结果

由此可见，系统设计的颜色识别算法，具有很好的适应性。无论是在哪种光照条件下，识别正确率都在95%以上。

5.2 魔方还原算法测试结果

设定的步数阈值是30步，时间阈值是5秒。算法若在5秒内找到30步以下的还原步骤就会结束搜索，返回结果，若时间超过5秒，则直接终止搜索，返回0。输入100个不同的随机打乱的三阶魔方，得到还原时间的分布如图9所示。

图9 魔方还原算法求解时间分布图

70%以上的情况，都可以在1 s内得到30步以内的正确还原步骤，平均还原步数为25步。HPS端系统主频仅有800 M，算法无疑是非常高效的。

5.3 还原系统整体测试结果

为测试整套系统的稳定性，进行了100次打乱魔方的还原。每次还原结束后，记录下结果，然后立刻随机打乱后放入系统启动还原。99次还原成功，仅在第92次还原时，因为前面累计的偏差，导致魔方顺时针旋转90°时，多转了10°左右，魔方被转乱，还原失败。魔方采集6个面颜色，耗时都在3 s左右，求解时间平均在1.5 s，机械结构还原时间分布如图10所示。

图10 机械结构还原魔方耗时分布图

99%的还原成功率，验证了系统机械结构的稳定可靠。平均40 s的魔方还原时间，验证了系统的高效，也让我们见证了FPGA和SoC协同工作所能产生的神奇效力。

6 结束语

本文在采用FPGA和ARM核异构平台的基础上，耗时3个月完成了快速魔方还原系统，该快速魔方还原系统由FPGA端实现摄像头图像采集和魔方色块RGB值的获取；HPS端完成颜色识别和魔方还原算法，再由FPGA实现对魔方还原机械结构精准快速的控制，从而完成实体魔方的还原。测试结果表明，该快速魔方还原系统能够快速地还原魔方，充分验证了SoC FPGA协同设计的高效。在未来，我们将进一步发掘两者各自的优势，实现更有价值的智能控制设计。