基于多种模型的递进式智能SOC估算

刘 民， 李少林， 张景明

(桂林电子科技大学 机电工程学院，广西 桂林 541004)

随着环境污染和不可再生能源短缺问题的加剧，发展可再生高效率清洁能源成为当今的热点，其中，电动汽车高效节能的特点深受人们的青睐。而动力电池是推动电动汽车前进的能源载体，决定整车的工作性能。电池的荷电状态(state of charge，简称SOC)定义为电池在一定放电倍率下，剩余电量与相同条件下额定容量的比值。电动汽车电池SOC估算的精度将直接影响电池的续航里程和使用寿命[1]。锂离子电池具有高能量密度、高比功率、充放电方便省时、使用时间相对较长、性能相对稳定，因此选用锂离子电池进行研究[2]。

目前，较为常用的电荷估算方法有：1)基于电池内部的电化学反应直接估算电池的SOC；2)基于外部特性参数建立等效模型的间接估算。考虑到电池内部的电化学反应比较复杂，常用间接法来检测电池的外部特性参数。间接法估算电池SOC主要有放电实验法、开路电压法、安时积分法、神经网络法、模糊逻辑法、卡尔曼滤波法、数据驱动法等[3-4]。针对锂离子电池非线性特点，采用FFRLS-EKF-SOC实现对锂离子电池进行SOC的估算。

1 等效电路模型及参数识别

1.1 2种电池等效电路模型

等效电路能够清晰地反映电池物理性质的特点，目前较为常用的等效电路模型有Rint型、Thevenin型、PNGV型、GNL型及二阶RC等效型[5]。本研究采用二阶RC及简化的GNL电路模型。图1为二阶RC等效电路，其中VL为电池外电路的路端电压，电压源VE为开路电压[5]。锂离子电池工作过程中的损失主要包括浓差极化环节(R1与C1并联)和电化学极化环节(R2与C2并联)以及欧姆损失RO。各个模块串联组成锂离子电池二阶RC等效模型[6]。

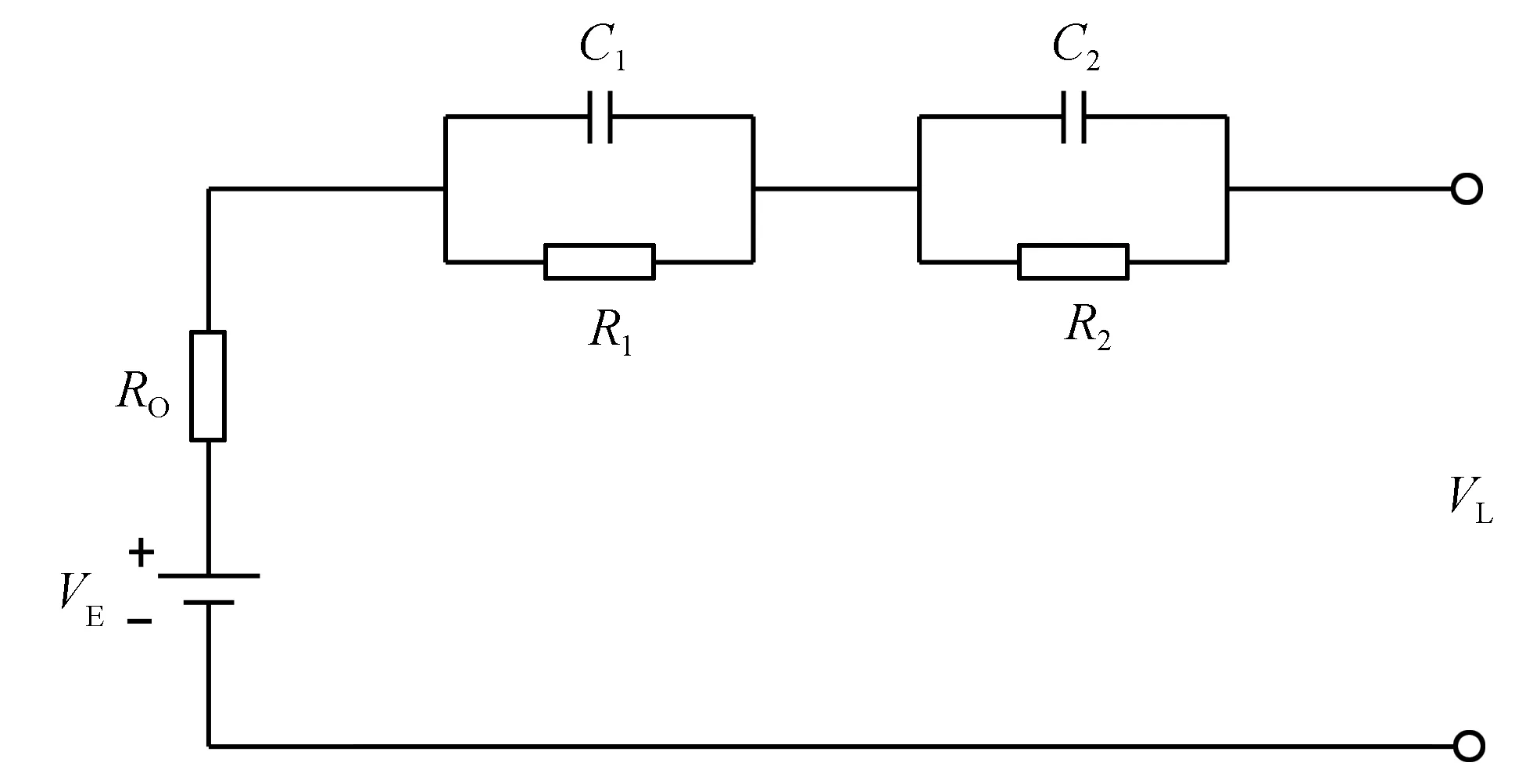
图1 二阶RC等效电路

对于图1的二阶RC等效电路，根据基尔霍夫电压定律与电流定律，可得如下方程：

VL,t=VE-V1,t-V2,t-IRO；

(1)

(2)

其中：VL,t为t时刻电池外电路端瞬时电压；V1,t为t时刻R1、C1并联瞬时电压；V2,t为t时刻R2、C2并联电路两端瞬时电压；I为t时刻电池内部瞬时电流。关于It的方程为一阶线性非齐次方程。假设电池放电时电流为正，充电时电流为负。设V1,0、V2,0为模型第1阶段、第2阶段极化初始电压，I为恒定电流，τ=RC为时间常数，t为电化学极化(浓差极化)时间，对式(1)、(2)求解可得：

(3)

(4)

(5)

GNL等效模型结构复杂,参数较多，基于GNL等效电路模型的辨识算法以及SOC估算中泰勒展开为高阶运算，计算较为复杂，不利于工程实现。为此，在GNL基础上忽略自放电因素进行简化，简化的GNL模型如图2所示[7]。

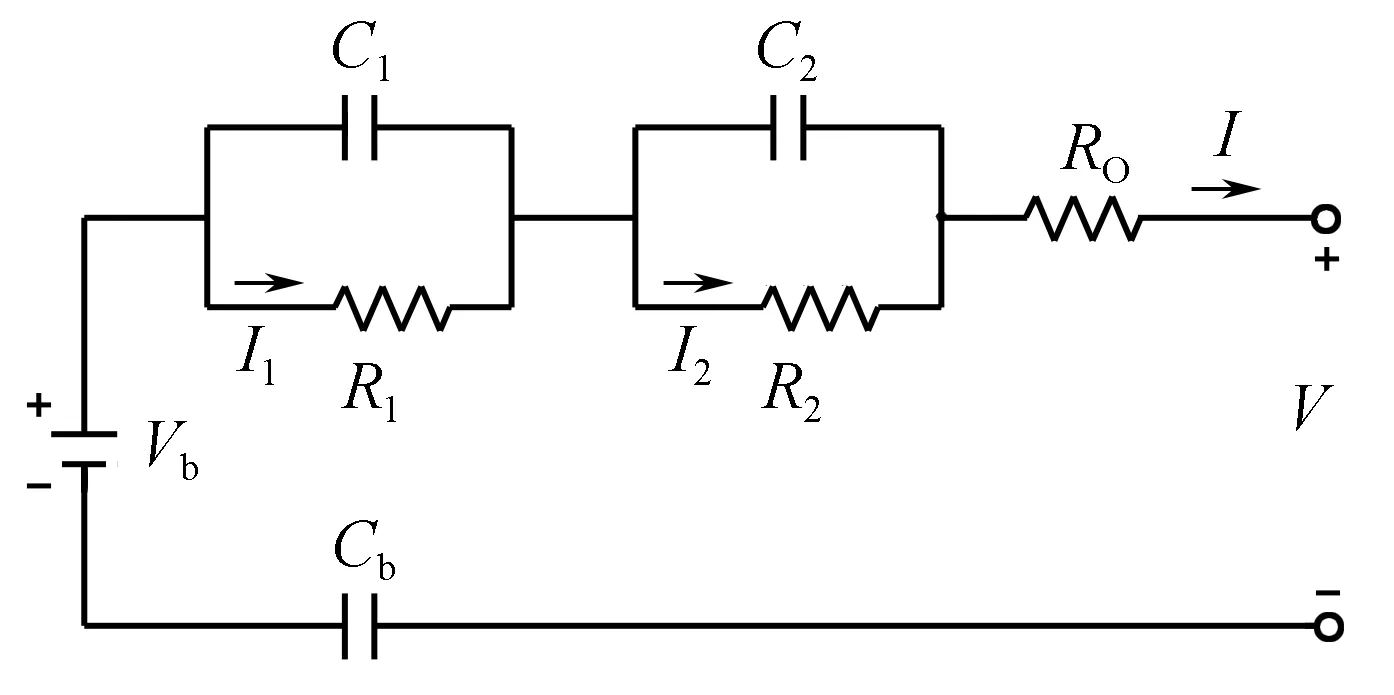
图2 简化的GNL等效电路模型

对于图2所示的简化的GNL等效电路模型，由电路关系可得到频域下的状态方程为

(6)

其中s为复数频率。

1.2 电池拟合参数

在ADVISOR平台获取锂电池典型工况下的动态过程参数。ADVISOR仿真平台中，选用gm_ev1_in车型、ESS_L17_temp型号锂离子电池进行UDDS仿真研究。根据基尔霍夫电流定律，使其流过电流ΣI=0，静置30 min，测得此时路端电压，即开路电压(OCV)VOC。以间隔10%的SOC进行启动仿真，测得10组路端电压数据。利用Matlab软件的polyfit工具对数据进行拟合，作出如图3所示的OCV-SOC拟合曲线。用ADVISOR软件进行UDDS工况下的仿真，此时OCV-SOC曲线表达式为

(7)

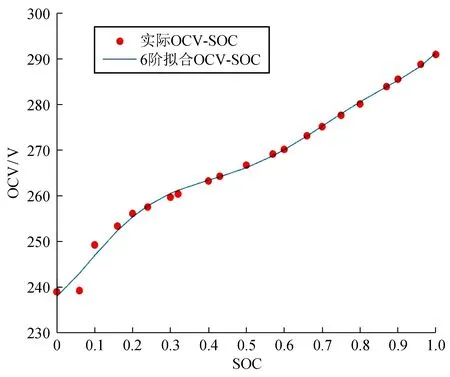
图3 OCV-SOC曲线图

1.3 等效电路模型参数的辨识

电池模型参数辨识主要有在线和离线2种方法。采用带遗忘因子递推最小二乘法进行在线参数辨识，解决了最小二乘法参数辨识的数据累积和饱和现象，减小了原始数据对观测精度的影响[8]。具体推导如下：

(8)

(9)

(10)

二阶RC电路模型的参数识别，根据图2电路,简化的二阶RC等效电路状态方程为

(11)

设τ1=R1C1，τ2=R2C2，c=R1+R2+RO，d=R1τ2+R2τ1+RO(τ1+τ2)，对表达式进行离散化处理，利用FFRLS算法进行参数辨识处理后参数值为：

简化的GNL简化电路模型的参数识别，根据图2电路，简化GNL等效电路状态方程为

(12)

对化简结果进行离散化处理，利用FFRLS算法进行参数辨识处理后参数值为：

通过离散参数推导可看出，两模型参数辨识结果基本相同，但是简化GNL模型为三阶方程，计算量比较大，而RC等效模型计算相对简单，所以采用二阶RC电路进行参数辨识。

2 基于电路模型的算法仿真

2.1 基于电路模型的改进EKF

根据定义，SOC的瞬时值SSOC,t可通过积分求得：

(13)

其中：SSOC,0为SOC初始值；η为放电效率；Qrate为额定容量[9]。对上式进行离散化可得，

(14)

其中：SSOC,k+1为第k+1个采样点的SOC值；ik为第k个点的采样电流。

综上，对于图1的二阶RC等效电路，其状态方程为：

(15)

VL=VOC(k)-V1(k)-V2(k)-ROI(k)+v(k)。

(16)

其中：Δt为采样时间；w(k)为过程噪声；v(k)是观测噪声；VOC(k)为高阶非线性函数的泰勒展开值[10]。则EKF的状态空间向量Xk、状态转移矩阵Ak以及控制矩阵Bk为：

(17)

(18)

(19)

D=[R0+RSOC(1-fSOH)]。

(20)

其中：R0为电池出厂时的内阻；RSOC为SOC当前时刻的欧姆内阻；fSOH为电池的健康状态因子，表示电池健康程度。根据电池容量衰减定义fSOH[11-12]为

(21)

其中：C0为初始电池的容量；C为当前时刻电池的容量；CEND为电池寿命终止时的容量。EKF算法是一个多次循环的过程，其具体流程如图4所示[13]。

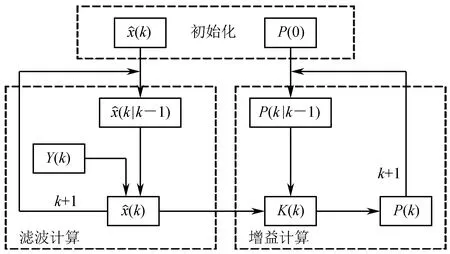
图4 EKF算法递推流程图

2.2 基于电池电路模型的FFRLS-EKF-SOC

EKF算法依赖于模型的精度，而锂电池工作在非线性模式下，导致内部参数也会发生变化，因此，需要在线更新电池内部参数，采用联合算法对动力电池SOC进行在线估算。采用遗忘因子递推最小二乘法参数辨识，将更新的参数运用到EKF算法中，估算当前时刻的SOC值。根据OCV-SOC关系曲线求出OCV，具体流程如图5所示。

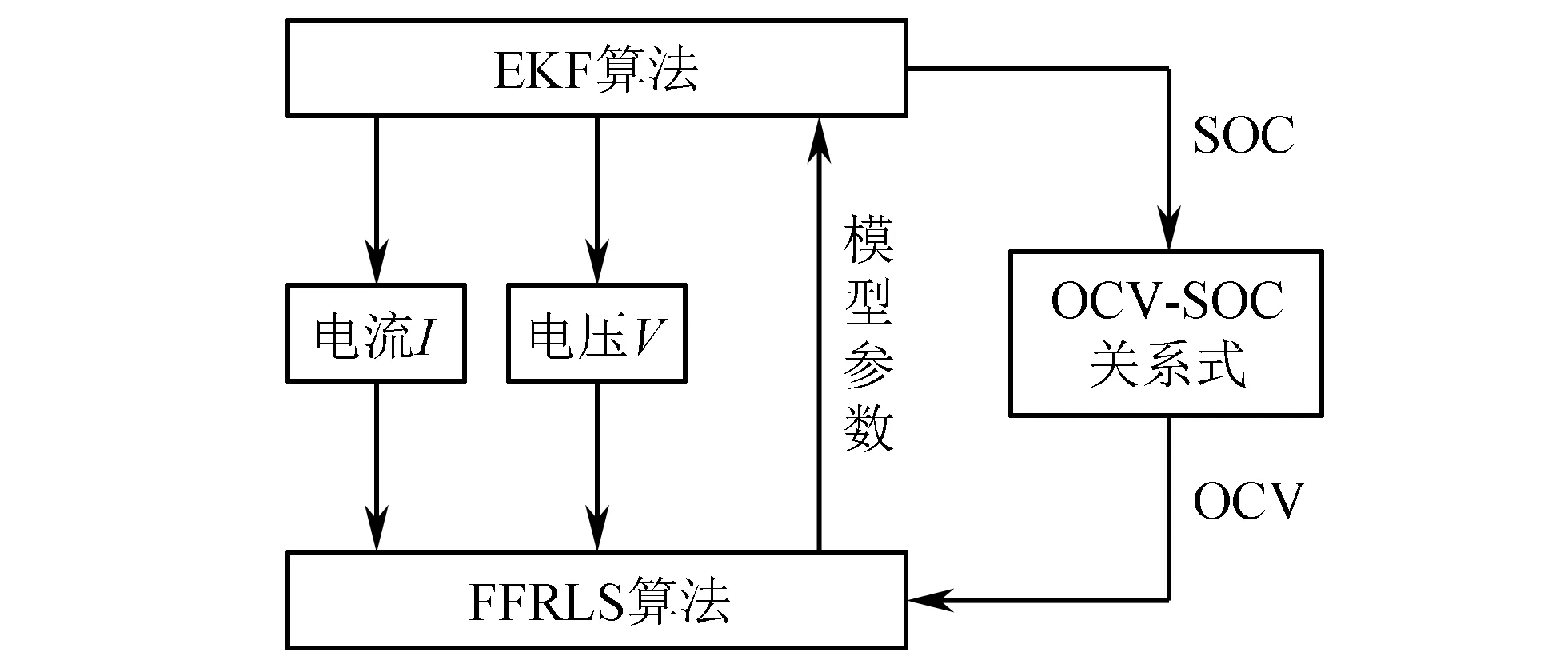
图5 基于FFRLS-EKF联合算法的SOC估算流程图

2.3 算法仿真结果及分析

在Matlab中，使用UDDS工况下的数据进行仿真，得到Ah-SOC、FFRLS-EKF-SOC与REL-SOC的SOC相对误差及SOC值对比如图6所示。从图6可看出，初始阶段安时积分法与FFRLS-EKF-SOC算法都具有较高的估算精度，但随着时间的积累，安时积分法的累计误差逐渐增大，采用FFRLS-EKF-SOC算法能减小累积误差，测得的SOC值与实际结果更为接近。采用FFRLS-EKF-SOC算法平均误差小于1.8%，最大误差小于3%。通过对比，选用FFRLS-EKF算法其整体误差较小，能够满足电动汽车动力锂电池SOC估算的需求。

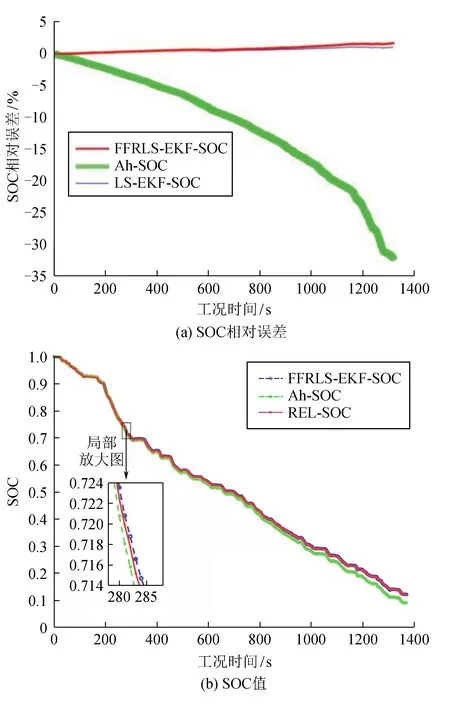
图6 UDDS工况下3种算法的SOC相对误差及估算值

3 实验验证与分析

为了验证FFRLS-EKF-SOC算法电池SOC估算的精度，通过实验进行分析对比。将数据源中电流和电压作为输入数据进行测试，利用仿真数据源中的运算结果与FFRLS-EKF-SOC算法SOC的估算结果进行对比分析，来评估FFRLS-EKF-SOC算法的估算精度。分别测试对比60组数据并进行对比分析，以其中7组为参考，对比结果如表1所示。从表1可看出，FFRLS-EKF-SOC算法SOC的估算误差均值小于3%，满足实验对SOC估算精度的要求。

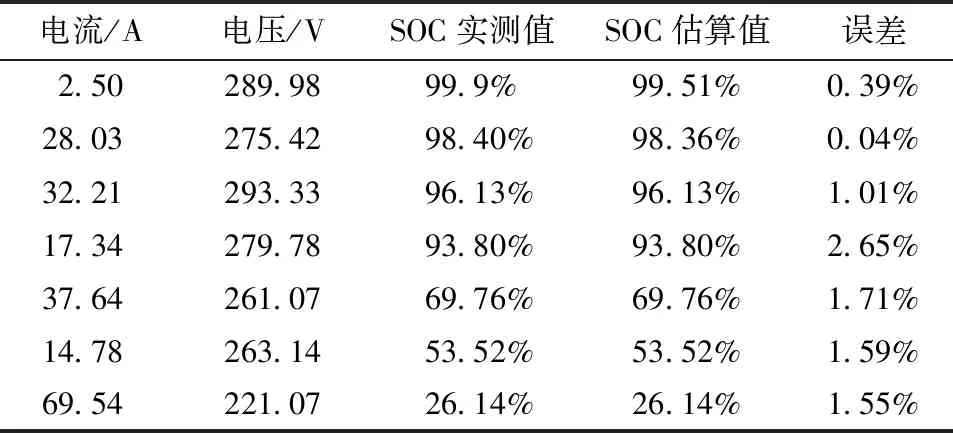
表1 系统对SOC估算测试结果

4 结束语

根据锂电池非线性的工作模式以及内部的化学损耗、电化学损耗、欧姆内阻等特点，建立了二阶RC等效电路模型和简化的GNL模型，采用最小二乘法分别对2种模型进行参数识别。选用二阶RC作为等效模型，采用FFRLS-EKF-SOC算法对锂电池SOC进行估算。在SOC估算中引入电池的健康状态因子，更加真实地反映出电池的真实状态，提高了电池SOC的估算精度。仿真实验结果表，FFRLS-EKF-SOC估算具有精度较高、对初值依赖小的特性。