基于重心法和层次分析法的高校快递智能柜选址布局问题研究

汤云峰

(华南理工大学广州学院，广东 广州 510800)

在高校电商快速发展的背景下，快递智能柜是目前校园电商物流“最后一公里”问题的主要解决方案。其中,快递柜的合理选址是影响客户体验的重要因素[1-3]。目前，关于高校快递最后一公里的研究主要集中在两个方面:一是高校如何与快递企业及第三方服务企业协同提高校园快递服务水平；二是智能快递柜在校园推广中遇到的技术问题、系统集成问题、成本及服务等方面的研究。而关于智能快递柜在大学校园的网点选址方面的研究，仅有少量文献。王海花等[4]从学生取件的角度出发，主要考虑学生到快递柜取件的总距离、快递柜的服务半径和各个需求点的快递需求权重，研究校园内智能快递柜的选址问题，该研究主要是针对单一需求点与单一服务点匹配的情况。丁猛[5]选择了集合覆盖模型研究大学校园智能快递柜备选网点的方法，针对网点数量最小和固定网点数量两种情况，分别建立适合大学校园的智能快递柜模型，但是未考虑用户的出行时间和快递的投递时间的约束。李淑芳等[6]通过集合覆盖模型研究最优网点规划方案，根据方案结果确定该区域内智能快递柜的最少数量，未着重针对具体位置选址进行研究。张晶蓉等[7]建立了以网点个数最少为目标，网点辐射半径和容量作为约束的集合覆盖模型，同时运用综合打分法找到最理想的网点布局方案，确保大学城内所有学生宿舍需求点都被网点覆盖，通过该研究模型能得到可行解但不能保证是全局最优解。邱晗光等[8]在顾客需求依赖末端交付方式与时间窗约束下，考虑配送量最优和配送成本最优，建立了“自提柜选址-时间窗分配-路线规化多目标联合优化问题模型”。该多目标模型较为复杂，影响了实用性，且难以得出多目标同时最优的解，需要在配送量最优和交付成本最优等目标之间进行权衡。

目前设施选址方法主要有定性分析法和定量分析法两类。定性分析法主要有专家打分法、Delphi法、模糊综合评判法等，此类方法具有简便易行、易于操作的优点，但是主观性较强，一般用于数据资料不足的情况。定量分析方法主要有重心法、集合覆盖模型、遗传模拟退火算法等，这类方法一般把选址问题转化为目标函数，再利用合适的算法求最优解。比起定性分析，定量分析更容易得到准确结果，但是一般需要较多数据资料，且计算过程比较复杂[9]。层次分析法(analytic hierarchy process， AHP)、DEA分析法、多目标决策法等选址方法，将定性和定量因素相结合，做出的分析相对更加全面。

为了进一步解决定性与定量相结合的问题， 本文综合考虑影响自提柜选址的各种因素，联合采用重心法和AHP法，提出一种简单、实用的校园智能柜选址方法。

1 研究方法

1.1 重心法

重心法即物流地理重心法，是把选址问题抽象成数学表达式，通过求解数学模型找出最优方案的方法[10]。该方法将物流系统的需求点看成是分布在某一平面范围内的物体系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心将作为物流网点的最佳设置点，利用确定物体重心的方法来确定物流网点的位置[11]。

重心法的模型计算公式如下

(1)

(2)

式中，待确定的重心位置的坐标即为(X0，Y0)，各个需求地的坐标即为(xi，yi)，mi表示的是每个需求地的需求量。

1.2 AHP法

AHP法是将最终决策的相关元素分解成目标、准则、方案等层次，然后再进行定性和定量分析的方法。该方法是美国运筹学家匹茨堡大学Saaty教授在为美国国防部研究一项课题时，提出的一种层次权重决策分析方法[12]。

AHP首先要将决策问题按总目标、各层子目标、评价准则直至具体的备选方案的顺序，分解为不同的层次结构，然后再用求解判断矩阵特征向量的办法，求得每一层次的各元素对上一层次某元素的优先权重，最后再用加权和的方法递阶归并各备选方案对总目标的最终权重，最终权重最大者即为最优方案。

1.2.1 构建层次分析结构模型

结构模型一般分为 3 层，分别为目标层、准则层和方案层。这样方便对整个决策问题进行结构研究分析，弄清决策的各个影响因素之间的关系。

1.2.2 构造两两比较判断矩阵

判断矩阵是从准则层开始，对各指标之间进行两两对比，并按9分位比率法对各评价指标的相对优劣顺序进行排序，即以数字1～9为标度值来构造出评价指标的判断矩阵。标度方法见表1。

表1 判断矩阵元素标度方法

1.2.3 计算各个标准和因素的权重

针对某个标准计算各因素的权重，然后进行一致性检验，即对每个矩阵计算最大特征根及相应的特征向量，然后采用一致性指标IC、随机一致性指标IR和一致性比率ICR做一致性检验。指标IC的计算公式为：

,

(3)

式中，n为矩阵的阶数。

若IC≤0.1，则可认为判断矩阵一致性可接受，否则需要重新进行两两比较。IR为修正值，ICR为修正平均值。计算式为：

(4)

1.2.4 方案层的层次总排序

确定某层所有因素对于最高层总目标的相对重要性，这一过程是从最高层到最底层依次进行的。对于最高层而言，其层次单排序的结果也就是总排序的结果[13]。

重心法是常用的选址方法，尤其是在单一设施选址问题中，较容易获得最佳的选址。但是其模型公式获得的选址一般不够精确，往往需要多次迭代计算来改进其计算精度，计算出来的位置在现实中也可能会因各种客观因素而无法实现，不得不在理想选址附近的合适范围内选定备选地址，再利用其他模型算法算出最优的选址位置。而AHP法适用于多因素且缺乏足够数据资料情形下的决策问题，是定性与定量相结合的系统分析法。因此，本文将重心法和AHP法相结合，来解决校园快递自提柜的选址决策。

2 联合采用重心法和AHP法选址的实例研究

图1 校区坐标分布图Fig.1 Distribution of campus coordinate

以广州某高校作为选址研究对象，联合采用重心法和AHP研究高校快递智能柜的选址方法，同时为该校选定最优的选址方案。

该校占地面积近2000亩(1亩=667 m2)，在校学生20 762人，现有学生宿舍楼22栋。每栋宿舍楼的学生人数如表3所示。从统计学的角度来说，每栋宿舍楼的收取快递的需求量与该栋宿舍楼的学生人数成正比，这里假设为每个学生同样时间内取件数都为1，因此可以用每栋宿舍楼的住宿人数来代替每栋宿舍楼的快递需求量数。

2.1 基于重心法进行初步选址

首先构建参照坐标，为了简便起见，在学校校区的平面地图上建立相对坐标系，相关参数参考该校的校园总平面规划图，并作四舍五入处理。如图1所示，用圆点标出每栋宿舍楼的中心位置，以学校中心区的图书馆所在位置为原点，以米为单位刻度，建立参照坐标系。每个宿舍楼的坐标如表3所示。

表3 需求量与坐标基本情况

利用重心法模型的计算公式，将表3中的数据代入公式(1)，(2)，得X0=147,Y0=592。

故重心坐标为(147,592)，如图2中A点所示。

虽然由重心法选址模型确定了理论中最合理的地点，但是现实中可能存在各种其他实际情况，因此还需要考虑理想选址地点在现实中是否有足够空间、在建设成本及运营成本中是否经济、师生取件是否方便等其他问题。因此，在使用重心法模型计算出坐标后，以该坐标为参考，在附近选择几个备选的地址。

在本例中，把重心点附近的可用地址罗列出来作为备选方案。再按照大学校园特点，将大部分学生都会经过的日常通勤路线上的可用地址罗列出来作为备选方案，然后再基于层次分析法对备选方案进行决策。

经实地考察，得到3种备选方案：第一种在重心坐标点A点处设置自提点，本例中是篮球场，设本方案为P1；第二种是在重心坐标点附近直线距离约130 m的B点处设置自提点，在本例中是一处校园饭堂附近的开阔地，设本例为P2方案；第三种是在距离重心坐标点直线距离约470 m的C点处设置自提点，此处是大部分学生去教学楼上下课会经过的宿舍楼的底层开阔地，设本方案为P3。如图2所示。

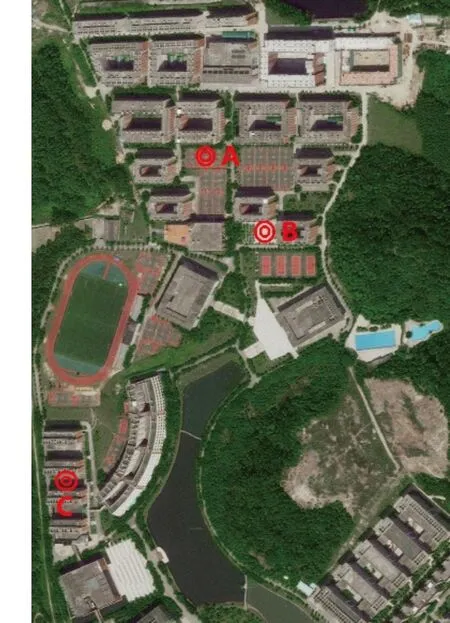
图2 重心位置及备选方案位置示意图Fig.2 Graph of Barycenter location and alternative position

2.2 基于AHP法对备选方案进行决策

2.2.1 构造层次分析模型

将重心法求得的两个备选地址A和B以及另一处备选地址C作为层次分析法中的3个备选方案，综合考虑4个影响因素分别是：方便程度、行走距离、设施条件、运营成本，在重心法模型确定的自提柜选址方案基础上建立的AHP模型如图3所示。

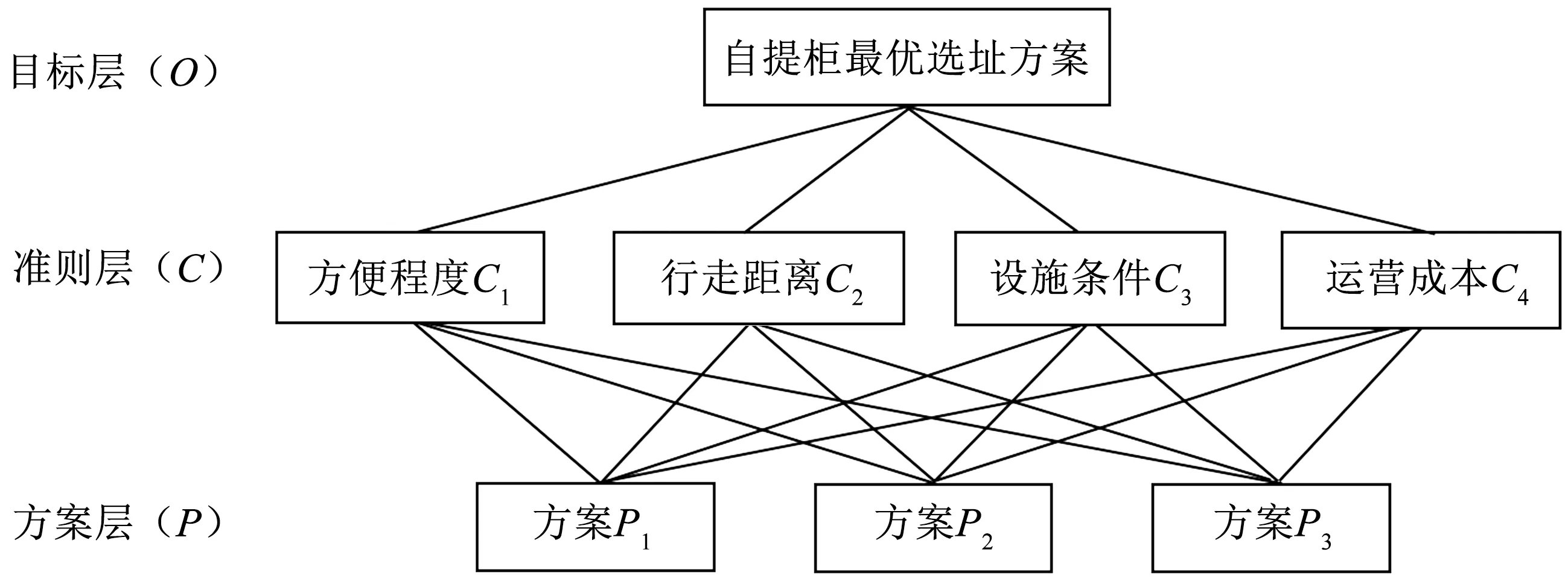
图3 评价指标体系图Fig.3 Diagram of evaluation index system

2.2.2 构造判断矩阵及一致性校验

本研究中邀请了6位相关专业人士，运用德尔菲法对自提柜选址4个影响因子进行赋值并两两比较打分，将评价结果转成判断矩阵A，如表4所示。

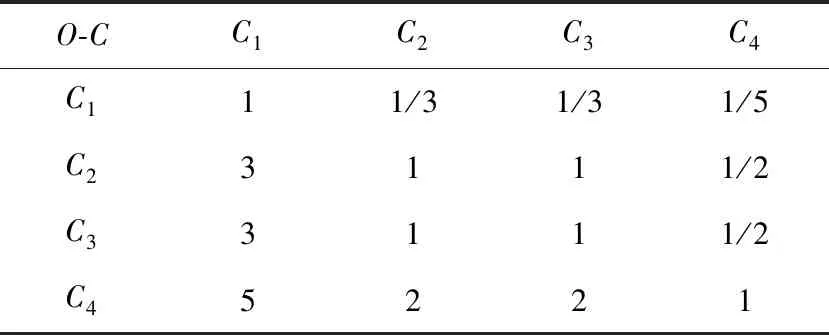
表4 目标层与准则层的判断矩阵A

对于此矩阵，对各列归一化得：

(5)

用原始矩阵A乘以ω，得：Aω=(0.328,0.941,0.941,1.799)T

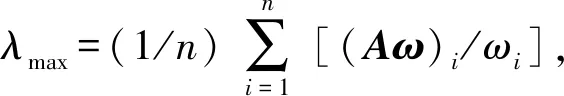
经检验，有满意的一致性，可认为由该判断矩阵所得的权重值合理。

对于方便程度C1准则，各种方案P1、P2、P3的重要性比较见表5。

表5 准则层C1与方案层的判断矩阵A

对于此矩阵，对各列归一化得：

(6)

用原始矩阵乘以ω，得：Aω=(1.200，0.600，1.200)T。

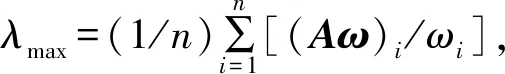
经检验，有满意的一致性。

用同样的计算方法，可得准则层与方案层的其他判断矩阵，具体过程不再详细赘述，直接列于表6中。

对于行走距离C2准则，各种方案P1、P2、P3的重要性比较见表6。

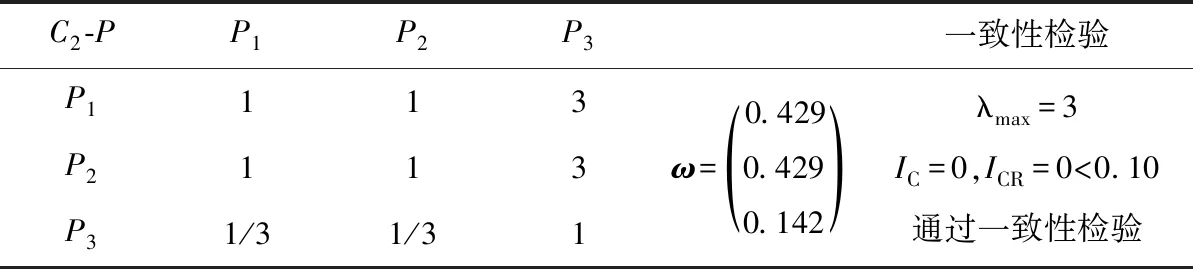
表6 准则层C2与方案层的判断矩阵

由表6中一致性检验过程可见，有满意的一致性，可认为由该判断矩阵所得的权重值合理。

对于设施条件C3准则，各种方案P1、P2、P3的重要性比较见表7。

表7 准则层C3与方案层的判断矩阵

由表7可见，一致性检验通过，可认为由该判断矩阵所得的权重值合理。

对于运营成本C4准则，各种方案P1、P2、P3的重要性比较见表8。

表8 准则层C4与方案层的判断矩阵

上述所有判断矩阵的一致性比率ICR皆不大于0.1，因而都通过一致性检验，各矩阵的特征向量皆各自代表了各备选方案相对于准则层的重要程度。

2.2.3 对备选方案的决策

根据以上分析，学校选择自提点定量分析权重表见表9。

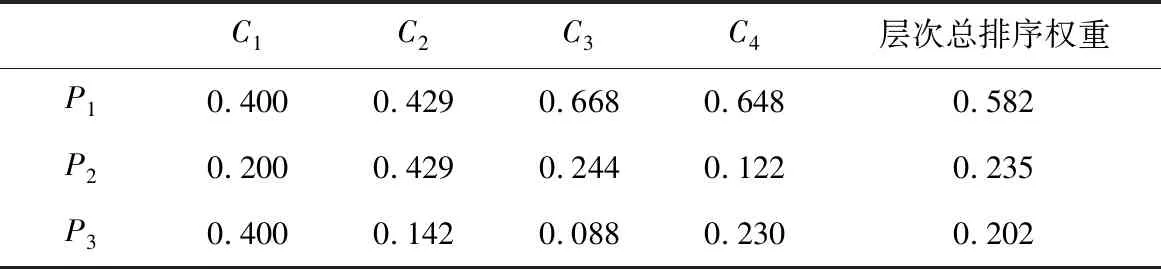
表9 各备选方案相对于目标层的权重

注：C1,C2,C3,C4的权值分别为0.082，0.235，0.235，0.449

根据方案层的3个备选方案总排序权重计算比较，得到方案P1的权重最大，因此，在3个备选方案中，P1为最优方案。

在本例中，选址结果与单一采用重心法的结论恰好相同，这可以理解为一种巧合，因为理论上二者之间可以不相同，重心法得出的选址结果受现实条件所限，有可能不具备可行性，比如理论计算的结果可能使得备选地址正好处在城市道路中央或居民建筑或商业设施中。而如果先由重心法计算出理论上的最佳地址，再在这个地址的合理范围内根据现实条件确定若干其他备选方案，然后结合AHP法的分析，考虑更多现实方面的因素，这无疑避免了单一选址的片面性。

3 结语

高校快递智能柜选址问题是随着电子商务发展而出现的新问题，本文将重心法和AHP法相结合，应用到校园自提柜的选址决策中。该方法计算过程简便明了，具有较高的科学性和可行性。本方法适用于一个快递自提柜网点即可覆盖全校的情况，今后，将进一步针对超大校园规模进行多网点选址的研究。