阴影影响下串联光伏组件输出特性分析
赵 辰 常宇健
(石家庄铁道大学电气与电子工程学院 河北石家庄 050043)
1 引言
光伏发电系统是由光伏组件、控制器、逆变器和储能装置等构成。光伏电池元是光伏组件最基本的单元,光伏电池元的输出电压大约为0.5V,容量较小,为了获得较大容量,通常把几十个甚至上百个光伏电池元进行串并联封装在一起构成光伏组件,光伏组件是光伏发电系统中的核心部件。随着光伏发电技术的广泛应用,光伏发电系统所处的环境也随之变得复杂,光伏阵列容易受到建筑物、树木、云层和鸟禽排泄物等所产生阴影的影响,使光伏阵列的输出特性变差,输出能量的能力变低,严重的情况下形成“热斑”现象,损坏了光伏电池,降低了光伏电池的使用寿命;同时,由于光伏阵列工作在局部阴影的条件下,使其伏安特性曲线呈阶梯形状,而功率特性曲线呈现多峰值形状,使常规的最大功率点跟踪方法失效,陷入局部极值点。故研究局部阴影条件下串联光伏组件的输出特性对于光伏发电系统的MPPT和转化效率至关重要。
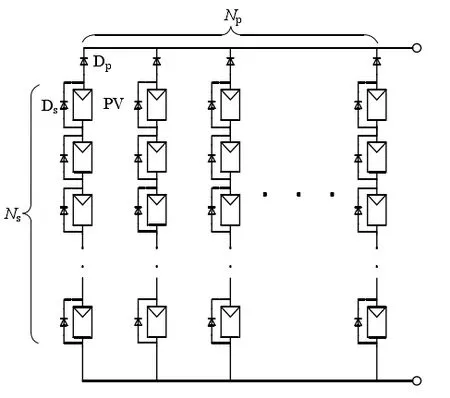
图1 光伏阵列结构示意图
本文以光伏组件工程模型为基础,结合电路理论知识,对带有旁路二极管的光伏组件串处于局部阴影时,根据旁路二极管的导通与关断两个阶段进行了详细的理论分析,从而得到了用分段函数描述处于局部阴影下的光伏组件的电流输出特性方程;最后,用实测与仿真的结果进行对比,结果证明了分段函数可以准确地描述处于局部阴影条件下的串联光伏组件。
2 局部阴影下光伏组件模型
在实际应用中,光伏电池的生产厂家只提供本产品在标准测试条件下的开路电压Uoc、短路电流Isc、最大功率点电流Im、最大功率点电压Um的数值。本文选择文献[1]中提供的工程数学模型如下:

当光伏阵列中,各个光伏组件特性相同时,由NS×NP个光伏组件构成的光伏阵列和单个光伏组件之间的关系[2]如式(2)所示:

式中:U、I、P为单个光伏组件的输出电压、电流和功率,Ua、Ia、Pa为光伏阵列的输出电压、电流和功率。
因此,在同一光照下光伏阵列的数学模型可以用方程(3)来表示:

当光伏阵列工作在局部阴影条件时,公式不在适用。
由于光伏电池对光照的变化比较敏感,在阴影的条件下,接受光照较低的光伏电池电压反偏,不在给负载提供能量,反而作为光伏系统的负载吸收其它正常光伏电池产生的功率,阴影下的光伏电池产生热量,使光伏阵列中产生“热斑”现象,降低了光伏系统输出功率和光伏电池使用寿命[3]。为了避免热斑现象,在实际情况下采用在光伏组件两端并联一个旁路二极管,由于在光伏组件两端并联了二极管,使得光伏阵列输出特性曲线发生了变化。此外,在光伏组件的串联支路与另一个串联支路并联前,需要先串联一个防逆二极管以防止光伏阵列输出功率过低时功率倒送对光伏组件的损害[4]。图1是一个典型的光伏阵列结构示意图,尺寸为NS×NP,其中,Ds为旁路二极管,Dp为防逆二极管。
将单串阵列中具有相同光照和温度的电池板称为子串;将具有相同遮挡模式的单串阵列并联在一起称之为子阵列。选取只有2个子串串联的单串光伏电池为基本单元建立串联光伏组件的数学模型[5]。正常光照的子串称为Z1,被遮挡的子串称为Z2,在非均匀光照强度下,子串Z1产生的电流Isc1不等于子串Z2产生的电流Isc2,并且Isc1>Isc2。
在外界光照强度、温度及光伏阵列拓扑结构等因素不变时,光伏阵列工作在输出特性曲线的什么位置由外界负载阻值决定。当外界负载阻值很小时,组件工作在大电流条件下,Z1迫使Z2流过比Isc2更大的电流,此时Z2的光伏电池受反压,使对应的旁路二极管导通,对Z2起到旁路保护作用,此时,只有组件Z1对外输出功率,而组件Z2及其对应的旁路二极管成为Z1的负载。随着外接负载不断增大,组件将工作在小电流条件下,组件的电流小于或者等于Z2产生的光生电流,其对应的旁路二极管开始形成反向偏压而截止,此时光伏组件Z1和Z2同时工作,向负载提供能量[6]。
综上所述,由2个子串串联的光伏组件电流方程可以用分段函数表示:

因此,根据式(3)和式(4),可以得到在任意阴影条件下光伏阵列的数学模型为:

式中Ix、Ux为式中提供的单串阵列模型
2 实验验证及仿真分析
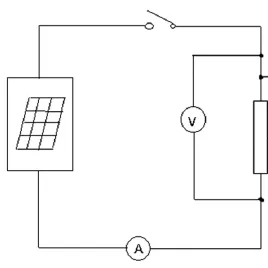
图2 测试电路图

图3 实验平台
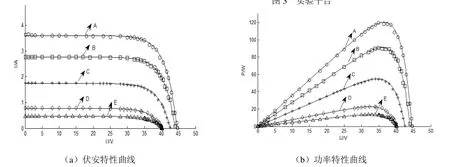
图4 均匀光照下的光伏组件输出特性曲线
为了验证上述模型的正确性,本文采用实验测试数据与计算机仿真进行比较。光伏组件采用的是由山东博泰公司生产的BTSM-180M型号,在标准测试条件下的参数为:最大输出功率Pm为180W、开路电压Uoc为43.2V,短路电流Isc为5.6A,最大功率点电压Um为35.9V,最大功率点电流Im为5.0A,它是由72个光伏电池元串联构成,每24个光伏电池元反并联一个二极管。测试电路图如图2所示,测试方法为将CH8715型号直流电子负载作为光伏组件的负载,通过不断调节直流电子负载的阻值来改变等效光伏负载的阻值大小,从而得到光伏组件不同负载阻值状态下的输出的电压、电流值。用SM206型号太阳能功率计测量光伏组件的光照强度,用Ti400型号红外热像仪测试光伏组件的温度,实验平台如图3所示。
图中各个各个散点为实测点,图中曲线是由计算机仿真得到的。图4是光伏组件在均匀光照情况下的输出特性。表1是对图4中不同测试条件下光伏组件输出特性分析的结果。
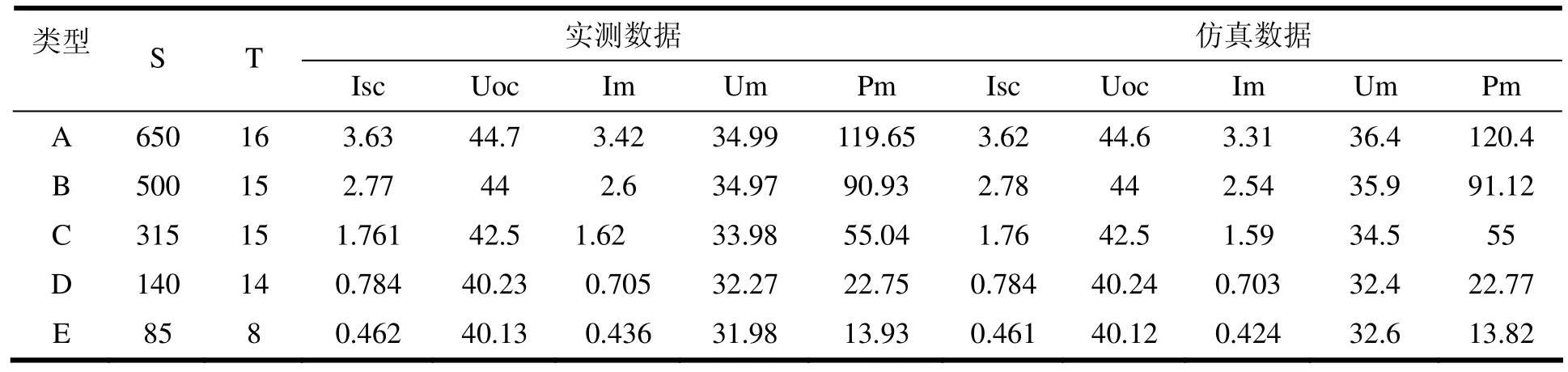
表1 均匀光照下的光伏组件的测试与仿真结果
图4(a)和图4(b)分别是光伏组件在不同的均匀光照强度和温度下的实测与仿真曲线。表1是对实测和仿真情况下的输出特性的分析,从图4中可以看出光伏电池既不是恒流源也不是恒压源,是一种非线性直流电源,伏安特性曲线呈单膝状,而功率特性曲线呈单峰状,存在一个最大功率点,实测与仿真得到的结果一致,实测曲线与仿真曲线在最大功率点处误差不大于1%。
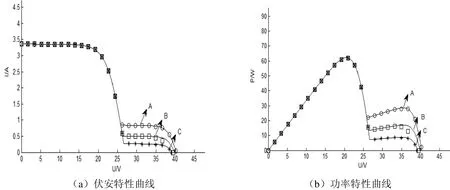
图5 阴影下光伏组件串输出特性曲线
图5是两个光伏组件串联时将其中一个光伏组件被阴完全遮挡影时的输出特性。表2是对图5中不同测试条件下光伏组件输出特性分析的结果。

表2 阴影下光伏组件串的测试与仿真结果结果
由于存在测量误差,造成由实测与仿真的特性曲线存在很小的偏差,光伏组件受到外界环境的变化造成输出特性曲线变化趋势,仿真与实验得出的结果是一致的。说明了分段函数可以准确地描述处于局部阴影条件下的串联光伏组件。同时,与均匀光照下的输出特性相比,处于局部阴影下的光伏组件的功率特性曲线存在两个峰值,使得传统的最大功率点跟踪算法失效,易陷入局部极值点,损失了真正的最大功率点。
3 结语
本文以光伏电池的工程模型为基础,通过对光伏电池旁路二极管的导通与关断两个阶段进行了详细的理论分析,从而得到了光伏组件及光伏阵列处于局部阴影时其输出特性方程,最后,用实测与仿真的结果进行对比,结果证明了该方法所建立模型的正确性。得到的结论如下:(1)根据光伏组件的工程模型所建立的仿真模型能够准确的放映光伏电池的输出特性,同时具有通用性;(2)局部阴影会造成光伏组件输出能力下降,使得伏安特性曲线呈阶梯状,功率特性曲线呈多峰值状,局部阴影下的光伏阵列的数学模型可以用分段函数较准确地描述;(3)在局部阴影条件下,串联光伏组件的伏安特性曲线呈阶梯状,而功率特性曲线呈多峰值状,使得常规的MPPT算法无法真正的跟踪到最大功率点,可能造成最大输出功率的损失,故寻找具有全局寻优的最大功率跟踪算法是今后一个重要的研究方向。

