基于DEM的流域地貌特征分形量化研究

陈 兵, 彭 芳, 李 鹏, 袁水龙

(1.西安理工大学 西北旱区生态水利工程国家重点实验室, 西安 710048;2.陕西省水利厅, 西安 710004; 3.陕西省水利电力勘测设计研究院, 西安 710001)

小流域是黄土高原生态环境恢复重建与治理的基本单元，其侵蚀产沙规律和水土流失防治一直是土壤侵蚀与水土保持学界研究的重点[1-3]。地貌形态是黄土高原流域降雨侵蚀产沙过程的重要下垫面影响因素之一，它在降雨动力、人为活动和地质构造运动等因素的共同作用下，通过水沙运移、能量消耗等方式实现其形态的不断演化，最终形成地形破碎、沟壑纵横的侵蚀地貌景观[4-5]。在已有的流域水土流失评价和预报模型中，诸多学者将流域高差比、沟壑密度、平均坡度、平均长度及沟谷切割深度等因子中的一个或多个作为流域水土流失预报模型中地形因子的量化参数[6-9]。但是由于地貌系统是一个非线性动态系统(Nonlinear Dynamical System，NDS)[10]，传统的地貌因子难以有效地表达这个非线性系统的复杂性，如地貌演化过程中的自组织性、突现性、自相似性、多尺度性及时空耦合性等特征，因此在流域水土流失评价和预报研究领域存在明显的局限性。分形理论的形成与发展为流域地形因子的整体性描述和地貌过程的非线性研究开辟了新的思路。但就目前而言，流域地貌的分形大多集中于水系分形研究，而对整个流域地貌形态特征的综合描述、地貌因子分形建模及其尺度范围(即无标度区)等方面问题有待进一步研究。本文以地理信息系统为平台，建立基于DEM表面积的流域分形布朗运动FBM地貌因子计算模型，并进行相关的GIS算法开发，以期能为黄土高原小流域降雨侵蚀产沙预报模型中的地貌因子量化研究提供新思路与新角度。

1 原理与方法

1.1 分形布朗运动理论

分形布朗运动理论是由Mandelbrot提出的描述自然界中随机分形的一种数学模型[11]。分形布朗运动的特点是具有统计自相似性即自仿射性(≈表示两者的概率分布相同)：

(1)

在应用FBM模型计算分形数据对象的分形维数时，关键是估计模型的非规则维参数即H参数。H参数估计是否准确关系到FBM模型对应用对象的适用性。采用绝对矩估计法，由公式(1)得到：

E[|BH(t+hs)-BH(t)|]=

‖h‖H·E[|BH(t+s)-BH(t)|]

(2)

两边取对数得到：

lnE[|BH(t+hs)-BH(t)|]=

H·ln‖h‖+lnE[|BH(t+s)-BH(t)|]

(3)

实际上等于：y=H·x+C。再由分形维数FD和Hurst指数H的关系得：

FD=DE-H

(4)

式中：DE为分形体的欧氏拓扑维数。

1.2 地貌分形量化模型

数字高程模型(Digital Elevation Model，DEM)是描述地面三维信息的常用模型，其数据结构是一种基于栅格模型的空间数据结构[12]。它将整个空间分割成大小相等紧密相邻的正方形网格，称为像元(cell)，高程信息以属性值的形式储存在相应的像元中。依托DEM进行数字地形分析，能够有效挖掘更深层的地形特征和地学现象，获取地形属性信息。随着地理信息系统的应用和普及，数字地形分析技术的优势和应用前景逐步为人们所认识，已成为进行地形模拟和地学分析的核心技术之一，在测绘、交通、军事、规划等相关领域被广泛应用。

对于DEM来说，s=(x，y)∈E2，代表DEM上各像元点位置。t=Z(s)，代表DEM上各像元点的高程属性值。若令A(t,s)代表DEM的统计表面积，则由分形布朗运动理论可将其推广到二维的情形，推导出一个与表面积有关的性质为：

(5)

lnA(t,rs)=H·lnr+lnF(t,s)

(6)

(7)

综上提出基于表面积的地貌特征分形量化模型为：

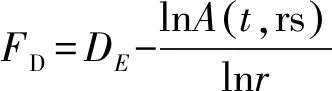
(8)

式中：FD为基于表面积的FBM流域地貌因子，DE为流域空间曲面的欧氏维数，对于表面积来说DE=2；r为DEM像元边长，A(t,rs)为像元尺度r下所测得的流域空间曲面表面积。

1.3 地貌特征分形量化的计算过程

规则网格DEM将地形曲面划分成一系列的规则网格单元，每个网格单元对应一个高程值。因此可以将其理解成由大量相同的小立方体单元“堆积”而成，小立方体边长等于像元的边长r，小立方体的高度为高程的属性值Z。计算每个小立方体的顶部水平面积及4个侧面的垂直面积之和就得到了整个DEM的表面积A(t,s)。为了避免重复计算，对每个像元只计算前面和左面的垂直面。r为像元尺度，AH为相邻像元高程之差，其中AH=r×r；AV1，AV2为相邻像元高程值之差与尺度r的乘积。设DEM的尺寸为M×N(像元个数)，DEM的表面积A(t,s)的计算如下[13]：

(9)

式中：Z(i,j)表示某DEM在尺度r下的高程值(i=1，2，…，M；j=1，2，…，N)。选定一条流域为研究对象，构建GIS实体模型，利用公式(9)就能计算DEM地形曲面的表面积A(t,s)。

式中基于表面积的FBM地貌因子的计算，实质上是将DEM像元尺寸逐步趋近于零计算极限的过程。然而在实际计算过程中所选定的DEM精度总是有限的，因此必须对所研究流域DEM的像元尺寸进行适当的选择(图1)。在尺度r下，求取表面积A(t，s)；变换像元尺度r，求出若干个相应的A(t，s)；将A(t，s)与r同取对数，并对两数列进行曲线拟合；利用统计软件求出lnA(t，s)相对于lnr的一阶导数，得到FBM地貌因子的Hurst指数H；最后由公式(8)计算得到基于表面积的FBM流域地貌因子FD。

图1 DEM像元尺度变化示意图

2 流域概况及计算过程

2.1 流域概况

陈家畈流域位于黄土高原中部黄土丘陵沟壑区第一副区，是大理河流域的一级子流域。该流域干流全长约为28 km，流域面积282 km2。流域地势西高东低，平均海拔1 100～1 700 m。流域地形复杂破碎，植被稀疏，水土流失严重。经过长期侵蚀，形成梁峁突起，沟壑纵横，镶嵌有墹地的黄土梁峁丘陵沟壑地貌。本研究拟以大理河陈家畈流域为例，对流域地貌特征量化因子的计算方法进行研究，并对FBM地貌因子的特征及应用进行探讨。

2.2 数据源与像元尺寸设置

在数字高程模型构建过程中，釆样是关键的一环。确定最优的数据采样密度和地表重建方法，都需要对地形表面形态特征有深刻地认识。本研究地貌形态GIS模型的创建选择由纸质地形图创建的方式，经过地形图扫描、几何纠正、影像二值处理与细化、等高线矢量化、数据接边、构建不规则三角网(TIN)、DEM的生成等步骤。

为了确保拥有足够的分析数据和DEM研究精度，这里将该流域地貌形态GIS实体模型的像元尺度分别设置18 m×18 m，20 m×20 m，22 m×22 m，24 m×24 m，26 m×26 m，28 m×28 m，30 m×30 m，32 m×32 m，34 m×34 m，36 m×36 m，38 m×38 m，40 m×40 m，45 m×45 m，50 m×50 m共14种规格，共生成14个小流域DEM模型。

2.3 计算过程

首先选取陈家畈流域18 m×18 m像元尺度DEM为研究对象，利用公式(9)求取表面积A(t,s)；然后依次变换像元尺度从20 m×20 m经过14次尺度变化到50 m×50 m，求出相应的A(t,s)；将所得表面积A(t,s)与像元尺度r同取对数，并对两数列进行线性拟合；确定相关系数最高的区间为无标度区间(R2≥0.99)；利用统计软件SPSS求出lnA(t,s)相对于lnr的一阶导数，得到地貌因子的Hurst指数H；最后由公式(8)计算得到陈家畈流域基于表面积的流域地貌特征分形量化因子 。

逐个计算陈家畈流域在不同像元尺度下DEM地形曲面的表面积A(t,rs)，再对变化的尺度r和对应的DEM表面积A(t,s)取对数，计算结果见表1。

表1 陈家畈流域地貌特征分形量化的计算成果

以lnh为横坐标轴，以lnA(t,s)为纵坐标轴将计算结果点绘在直角坐标系上，确定相关系数最高的区间即像元尺度18 m×18 m—36 m×36 m为无标度区间(R2≥0.99)，通过在该无标度区间内观察利用最小二乘法进行一阶线性拟合，见公式(10)：

(10)

将计算结果代入公式(8)中“基于表面积的地貌特征分形量化模型”，就可以计算得到陈家畈流域基于DEM表面积的流域地貌特征分形量化因子为FD=DE-H=2.0127。

3 结果与分析

3.1 地貌形态特征的标度不变性

标度不变性是分形量化模型应用的最大优势。从图2可以看出，当像元尺度大致处于18 m×18 m—36 m×36 m区间时，lnA(r)-lnr拟合的一阶线性方程的决定系数R2均达到0.99以上。说明在此区间内ln 与lnr表现出良好的相关性，并且呈现出明显的线性分布特征。此时lnA(r)与lnr的增量比值不随lnA(r)的变化而变化，呈现出标度不变性特征。lnA(r)与lnr的比值具有统计意义上的自相似性，地貌形态表现出了分形性质，此区间应处在无标度区之内。当像元尺度处在36 m×36 m以上时，线形的总体走向趋于下弯，lnA(r)与lnr的比值不能保持稳定。lnA(r)-lnr的线性分布特性消失，此时地貌形态的分形性质也随之消失，此区间应处于无标度区之外。

图2 拟和直线示意图

无标度区间的确定是分形维数应用的重要前提条件。在进行分形维数比较时应特别注意，无标度区间的确定方法必须是统一的，另外只能对处于同一个无标度区间内的分维进行比较。由图2可知，在18 m×18 m—36 m×36 m范围内(R2≥0.99)，陈家畈流域基于DEM表面积的FBM流域地貌因子为2.012 7，即当像元尺度处于这个范围时，流域地貌特征可以用一个分形维数表征。

因此，无标度区间的确定也就为不同像元尺度的流域地貌特征之间的比较与评价提供了可能性。另外由于18 m×18 m—36 m×36 m范围刚好处于常规高精尺度地形数据的尺度范围，这样也为高精尺度分布式地貌量化因子的开发和推广应用提供了新思路。

3.2 地貌形态特征的综合性表达

通过以上分形计算过程可以看出，流域地貌特征分形量化因子能够对流域三维地貌特征进行综合表达。lnA(t,s)实际上反映了整个流域表面的起伏特征，是对整个流域表面复杂度的总体表征。对于具体流域而言，其像元尺寸一定时所对应的lnA(t,s)值越大，流域地貌的起伏变化越强烈，流域表面越复杂，反之亦然。因此lnA(t,s)与lnr的增量比值，即流域地貌特征分形量化因子反映的是整个流域的总体性综合性特征。

准确有效地评价流域地貌特征，有利于了解和辨别地形地貌演变的客观规律和整体特征。一般来说，流域地貌形态分形量化因子D的取值范围为2～3。当D的取值为2时，流域表面趋于二维平面，流域地貌形态最简单。当D的取值为3时，流域表面趋于三维立方体，流域地貌形态也相对简单。只有当D=2.5时，流域地貌形态处于布朗随机运动状态，此时地貌特征处于最杂乱和无序状态，即地貌形态破碎和复杂程度的临界值，越远离D=2.5流域地貌特征的破碎程度越低。两种变化方式表征意义不同，当D从2.5增长到3时，地貌特征的演变处于正向堆积隆升阶段，趋于形成规整的塬台地貌。当D从2.5减小到2时，地貌特征的演变处于负向侵蚀拗陷阶段，趋于形成平坦的平原地貌。

3.3 地貌形态特征与传统地貌因子的关系

为了更加有效地对流域地貌形态特征FBM量化因子进行研究。在ArcGIS平台下，分别计算陈家畈流域在18 m×18 m—36 m×36 m像元尺度内的沟壑密度、地形起伏度、平均坡度、流域中值高程等地貌形态单因子指标，并与FBM流域地貌因子进行对比分析。可以看出当像元尺度处于18 m×18 m—36 m×36 m范围时，沟壑密度、地形起伏度、平均坡度、流域中值高程等地貌形态单因子指标分别呈现不同的变化形态。

随着像元尺度的增大，沟壑密度呈现先减小后增大的趋势，地形起伏度不断增大，平均坡度不断减小，流域中值高程呈现先平稳后增大最后减小的趋势。然而在此过程中FBM量化因子的值始终稳定在2.012 7处，其几何形态始终处于其他各因子曲线的中间区域，表现出与其他各因子曲线几何形态的“均值”形态相似的特征。亦即FBM量化因子蕴涵了各个地貌形态单因子的“综合叠加”特点，因此是对流域地貌形态特征的综合性表达。

4 结 语

流域地貌特征的综合量化指标不仅是数字地形分析的重要参数，而且对地形数据压缩、地形分类、测绘可视化、雪线分布、生物多样性、地形仿真、土地利用、导航定位、空间分析等研究领域有重要的研究意义，备受国内外研究人员的关注。本文提出的基于DEM流域地貌特征分形量化因子计算模型，利用分形维数的标度不变性，实现了一定的像元尺度范围内流域地貌形态特征量化指标的尺度不变，从而可以实现不同像元尺度下地貌形态特征的比较与评价。FBM地貌因子克服了传统地貌形态单因子指标的不足，可以对流域地貌形态特征进行综合性表达，为地貌因子量化研究提供了新思路与新角度。但是由于流域地貌特征分形量化计算模型的地域适应性还需要经过更多地貌类型的验证，后续研究重点应该继续放在对其他地貌类型区的检验方面，并在此基础上更加深入的探讨分形量化模型的普适性问题。