桥梁两支点转体施工技术的可行性研究

郭昭赢

（中铁十一局集团第二工程有限公司 湖北十堰 442013）

1 工程概况

武汉市常青路主线高架桥CQ27-CQ29#墩处采用（95+105）m连续钢箱梁桥跨越汉口火车站南咽喉岔区。为了减少高架桥施工对既有营业线的影响，采用转体法施工。转体主墩CQ28#墩下部结构为钻孔桩基础、分离式承台，门式墩身和盖梁，转体球铰安装在盖梁顶面中央位置［1］；上部结构为分幅变高度直腹板钢箱梁，球铰支点处梁高6.5 m，端部梁高3 m，直腹板梁高按二次抛物线变化，钢箱梁单幅梁面宽25.5 m，底宽16.5 m，双幅桥面总宽51 m，在球铰支点处沿桥长方向9 m范围左右幅钢箱梁为整体横梁设计，其余为分幅钢箱梁，球铰支点位于钢横梁中心。转体部分全长135.2 m，其中跨汉口火车站长臂端梁长91.4 m，三环线侧短臂端梁长43.8 m，转体角度81°。

2 两支点转体系统

因受施工场地限制采取不对称转体［2］，球铰支点两端梁体重量差3 000 t。若采取短臂端配重的常规方案使梁体平衡，一方面3 000 t重的配重块堆载在短臂端桥面，经计算此工况下钢横梁应力将超出可承受允许应力值，结构将会被破坏；另一方面因堆载面积有限，配重块堆载高度将达到4 m，并且梁体在配重块的作用下将产生下挠，在转体过程中难以确保配重块的稳定性。经研究并结合有限元分析计算，采用两支点转体方案：在短臂端配重2 644 t，同时在长臂端距离转体球铰中心23.6 m处设置转体辅助前支撑，通过前支撑与配重共同作用，使转体球铰支点两端达到平衡状态；同时依靠前支撑上的动力系统带动钢箱梁水平转体至设计位置，最后合龙。转体系统主要由墩顶中心球铰、辅助支撑轨道梁［3］（下部结构、轨道系统、滚轮小车、驱动系统、控制系统）和前支撑组成，如图1～图3所示。为论证该转体方法的可行性，按桥梁实体尺寸的1／5制作钢结构模型，通过收集模型转体过程中相关参数来指导实体桥转体施工。本文主要介绍极不对称两支点转体系统模型试验研究技术，重点在于模型的设计和转体数据的监控与分析，从而论证极不对称两支点转体系统施工技术的可行性。

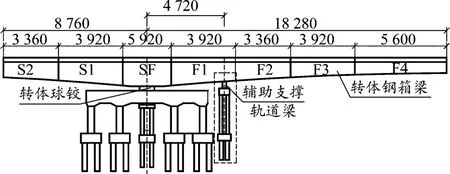
图1 转体模型结构立面图（单位：mm）

图2 转体模型平面图（单位：mm）

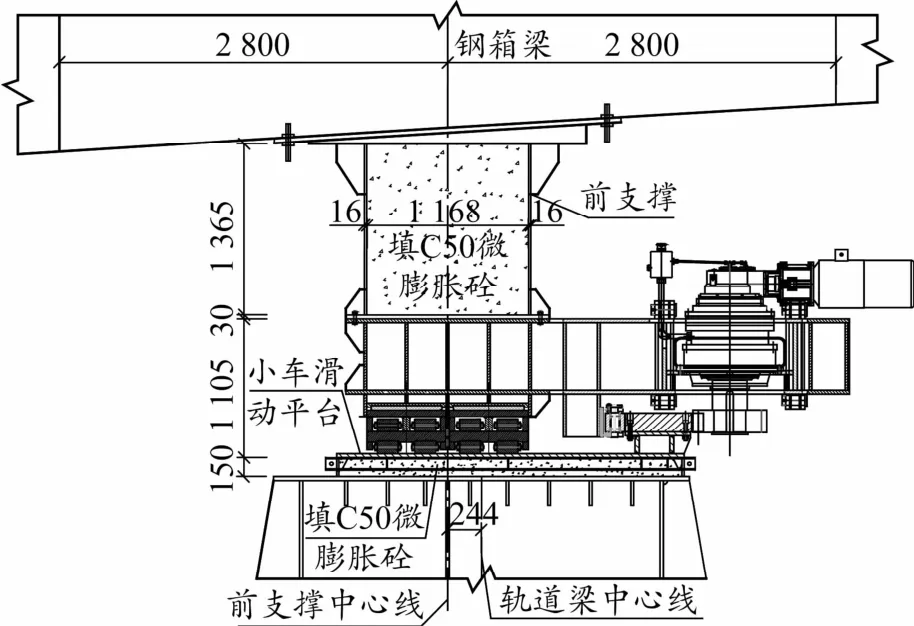
图3 两点转体系统立面图（单位：mm）

3 模型设计

3.1 尺寸的选取

本试验模型以等应力为原则，运用结构模型相似理论，按照长宽高比例为1∶5，即S1＝1／5，以等应力为原则［4］，设计制作了连续箱梁桥转体结构试验模型。该模型的相似关系如表1所示。钢箱梁截面复杂，制作难度大，在保证模型截面面积、惯性矩满足相似关系的前提下，对截面进行细部了微调。

表1 模型相似关系

3.2 材料的选取

模型设计材料采用与实桥相同的材料制造，钢箱梁主体结构、轨道梁、前支撑和滚动小车均采用Q235级钢板制造，球铰支座及扩大基础、轨道梁基础均采用C40混凝土。

3.3 配重计算

3.3.1 结构配重

表2 转体结构试验段模型尺寸

3.3.2 平衡配重

辅助支墩设计时考虑最大受力为1 000 t，中心球铰最大受力为9 000 t，现以64.24 t／m为原型理论配重，配重范围为19.6 m，单幅理论实际配重64.2×19.6＝1 258.32 t。此时的辅助支承支反力只有776.7 t，球铰承受反力为7 058.4 t。按照相似比，可以算出模型需要的理论配重值，即相应各支撑的支反力，单幅配重大小1 258.32／25＝50.33 t［5-7］。

4 试验模型测点布置

4.1 桥梁线形测量

为了控制模型钢箱梁施工的标高，为以后各节段高程控制提供观察的基准点，拟在各节段顶面横隔板的左中右三处设置水准控制点。同时在转体过程中，通过自动采集系统监测转体过程中倾角传感器的信号变化，从而监控转体过程中倾斜情况［8-10］。

4.2 桥梁应力监测

选择结构受力最不利位置作为测试截面：沿桥长方向SF-F1、SF-S1和辅助支撑处共3个截面的应力和剪应力，同时在每个截面的顶底板各布设4个测点。左右两幅钢箱梁在SF节段为整体设计，钢箱梁如同一个大横梁立在中心球铰上将左右两幅连接起来，防止转体过程中桥体发生翻转，在球铰两侧的横梁底、顶板各布置2个测点［11-12］。

4.3 转动系统受力监测

4.3.1 辅助支撑受力监测

八角枫水提液高剂量组有3只大鼠死亡，阳性组和八角枫水提液中剂量组各有1只大鼠造模失败，其余大鼠均造模成功。造模后第7天，除空白组外的其余各组大鼠足部均出现绿豆大小的溃疡，并逐渐结痂愈合；造模后第12天，除空白组外的其余各组大鼠足趾均皮肤发红、发热，轻度肿胀；造模后第14天，除空白组外的其余各组大鼠足底及踝关节均肿胀明显，关节僵硬，活动量减少，饮食减少，毛发失去光泽，体质量增长较空白组缓慢，部分大鼠见稀便；造模后第21天，除空白组外的其余各组大鼠足底及踝关节肿胀程度均较模型组明显减轻，活动及饮食量有所增加，体质量逐渐增加。

辅助支撑处的支反力是监控的重点，在转体前及转体的过程中，要时时监控辅助支撑的支反力，防止转体过程中的某些因素导致支撑力增大，将支撑轨道梁压坏，导致转体困难。故采用应变计监控辅助支承受力，应变计共设4个，分别设在辅助支撑钢管立柱外壁四周。

4.3.2 轨道梁受力监测

支撑轨道梁应力和位移监测。该轨道梁共有18跨，为制作方便，原来的普通钢箱梁截面简化为刚度相等的普通钢板拼装截面，测试截面选取关键的7个截面，每个截面有3个应力测点和2个位移测点。

5 模型试验测试结果

5.1 转体过程桥面倾角变化

模型桥布置了4个倾角传感器（见图4），固定放在左右两幅中间翼缘板处，用于监测转体过程中桥梁在顺桥向和横桥向的倾斜情况，实施监控转体情况。

图4 倾角测点布置及编号

转体过程桥面倾斜变化测试结果见表3。由表3可见，转动过程中桥面倾角在50%配重时E4处最大为-0.42°，100%配重时 E3处为0.3°，这种情况仅发生个别时刻突变（个别位置轨道顶面平整度不足），大多数情况桥面倾角变化范围都在0.1°以内，转动平稳。因此，实体桥时应注意轨道顶面平整。

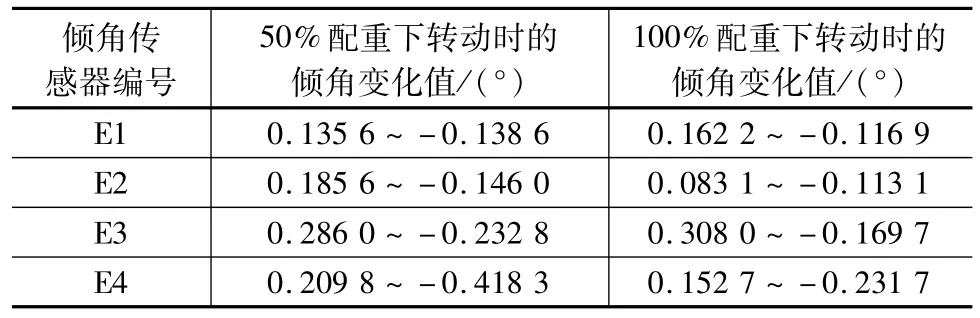
表3 模型转体过程中倾角变化值

5.2 转体过程挠度变化

下挠测点在距离左右两幅的长臂端1 m处，平均每2 min读1次数，无配重工况下测量了18次，最后一次为转动还原后的挠度变化；50%配重工况下共测量了17次，最后一次为转动还原后的挠度变化；100%配重工况下共测量了17次，最后一次为转动还原后的挠度变化。图5～图7为转动过程中的长臂端挠度变化测试结果。

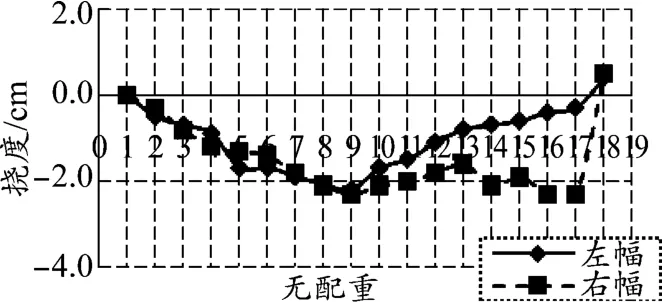
图5 模型结构自重工况下转动时的挠度变化

模型结构无配重情况下顺转时长臂端度最大变化2.2 cm，回到位后左右两幅挠度与顺转前相比最大变化为0.5 cm；50%配重顺转时长臂端度最大变化2.5 cm，回到位后左右两幅挠度与顺转前相比最大变化为0.9 cm；100%配重顺转时长臂端度最大变化3.6 cm，回到位后左右两幅挠度与顺转前相比最大变化为0.4 cm。从这些结果可以得出，转体过程中长臂端度变化较小，且回转到位后变化也较小，说明转动平稳。

图6 50%配重工况下转动时的挠度变化

图7 100%配重工况下转动时的倾角变化

5.3 转动过程应力变化

表4 模型转体过程中各应力变化

5.4 辅助支撑反力变化

本实验模型的反力测试不采用常规的方法，采用新的测量方法——应力测量法。整个转动过程中通过应变片的变化来预测支反力的变化。根据测量数据整理分析如表5所示。从表5可知，模型转动过程中前支撑反力在50%配重和100%配重情况下最大变化量为2.7 t，相对变化率最大为9%，转动比较平稳。模型结果与理论相吻合。

表5 模型转体过程中前支撑反力变化

6 模型试验结论

从本次模型试验测试结果，可以得到如下结论：

（1）模型的挠度测试结果与理论结果比较吻合，长臂端最大挠度12.50 cm，略大于理论值10.80 cm。实桥施工阶段应注意控制前支撑竖向位移对长臂端挠度影响，建议适当提高前支撑处梁底标高。模型转动过程中长臂端度挠度最大变化3.6 cm，回转到位后挠度与顺转前相比最大变化为0.4 cm，说明转体系统转动平稳。

（2）模型箱梁应力最大为142.35 MPa，理论分析结果为162.82 MPa，平均相对误差8%，绝大多数测点应力误差在10%以下，试验结果和理论吻合较好。模型转动过程中箱梁最大应力变化8.4 MPa，相对变化率8%；轨道梁最大应力变化5.8 MPa，相对变化率9%。

（3）箱梁横梁处最大应力为194.13 MPa，理论为180.72 MPa，平均误差为9%。

（4）轨道梁挠度最大为0.42mm，理论值0.42mm，平均偏差为8%；测量应力最大为61.4 MPa，理论分析最大为62.0 MPa，平均偏差8%。除了少数点误差较大外，绝大多数点误差均在允许范围内，整体试验与理论吻合较好。

（5）转体模型前支腿反力最大偏差为8%，与理论吻合较好。

（6）模型转动过程中桥面倾角变化在100%配重时为0.3°，这种情况仅发生个别位置（个别轨道梁接缝处），大多数情况桥面倾角变化范围都在0.1°内。因此，实体桥时应注意轨道梁顶小车走行面平整度控制。

（7）模型转动过程中前支撑反力在50%配重和100%配重情况下相对变化率最大为7%，转动比较平稳。

综上所述，该转体模型转动过程中各监测参数与理论吻合较好，转体系统转动平稳，既可顺转也可回转，验证了两支点转体系统的可行性。建议：适当提高前支撑处梁底标高，严格控制轨道梁轨道面的平整度，应考虑滚动小车滚轮曲线行走时内外半径变化。