基于半功率带宽法的行波超声电机谐响应分析

刘 军，朱 华，牛子杰，赵淳生

(1.南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京 210016；2.西北农林科技大学 机械与电子工程学院，陕西 西安 712100)

0 引言

超声电机(USM)是一种新型微特电机，其工作原理是利用压电材料的逆压电效应激发弹性体(定子)在超声频段内的微幅振动，并通过定、转子(动子)之间的摩擦作用将振动转换成转子(动子)的旋转(直线)运动，输出功率，驱动负载。其中，行波型旋转超声电机(TRUM)是目前最具代表性且实际应用最多的一类超声电机。而作为驱动行波超声电机工作的关键部件，定子组件(粘贴有压电陶瓷的弹性体，以下简称定子)的设计情况对电机的输出性能有着重要影响[1]。

近年来，主要利用有限元方法对行波电机定子的振动特性进行模态分析和谐响应分析，从而获得定子弹性体的振动模态参数。由于求解计算均在成熟的计算机软件中进行，故节省了大量人工用时，并提供了较可靠的计算结果。然而，有限元仿真结果的准确性是建立在模型材料固有属性设置的准确性之上，尤其是在谐响应分析时，结构阻尼比、激励等条件会对定子响应振幅产生很大影响，以致于干扰了研究人员的设计选择。因此，定子的有限元模型参数越准确，计算结果越逼近实际的振动效果。但是，大多研究者仅使用模态分析来得到定子的各阶固有频率和振型，进而选取符合预期的工作模态来设计定子，接着用样机进行实验来确认与仿真结果的一致性[2-3]；部分研究者在模态分析后进行谐响应分析，得到了响应振幅的仿真结果，但并未进行实际测试，只能看作设计结果的参考，不具有准确性[4]；此外，对谐响应仿真结果影响较大的模态阻尼比，部分文献只提到进行了人为设置，并未给出参数设计依据[5-7]；还有文献利用半解析法算出定子的模态频率、振型及振幅，并通过激光测振系统进行实验验证，结果较吻合[8]，但解析法不够直观，计算工作量大，且不利于定子参数化快速设计与优化。

本文以所在单位研制的一种中空行波超声电机TRUM-70H为研究对象，通过激光测振系统获得了电机定子振动模态频率和响应振幅，利用半功率带宽法求出定子工作模态的阻尼比，建立了有限元模型并进行谐响应分析，得到工作模态及其前后两阶模态的频率、振幅，对比激光测振结果发现仿真结果基本吻合。为了进一步验证该有限元模型谐响应分析的准确性，本文将对定子振动特性影响较大的齿特征(齿高和齿距)做参数化处理，并用有限元变量分析法仿真了齿特征参数变化对定子模态频率和振幅的影响。从中选取一组能降低电机转速，提高输出扭矩的齿特征参数替换原来的几何参数，再次进行谐响应分析并加工制造出新样机TRUM-70HA。同样地，对新样机定子进行激光测振分析，测振结果与谐响应仿真结果吻合，验证了有限元谐响应分析的准确性。最后分别对70H和70HA电机做了机械特性测试，结果说明新样机的空载转速更低，堵转扭矩更大，符合预期设计。

1 定子工作模态阻尼比的测定

1.1 半功率带宽法测定阻尼比原理

中空行波超声电机的定子沿周向展开可以近似看作一个梁，因此，其振动特点可采用梁的受迫振动理论进行分析，而梁的强迫响应是各阶模态响应的叠加，对于梁上某一点，其位移就是各阶模态响应在该点位移分量的矢量和[9]。对于70H电机而言，其压电陶瓷的极化分区是按照B011振型设计的，故其定子理想的工作模态是由各低阶模态叠加产生的B011“纯”模态。进一步用单自由度系统受迫振动响应的一阶模态做理论分析。单自由度系统在简谐激振力的作用下，其运动微分方程可写为

(1)

式中：M，C，K分别为单自由度系统的质量、阻尼和刚度系数；F0为激振力幅值；ω为激励频率。由微分方程理论解得稳态位移响应为

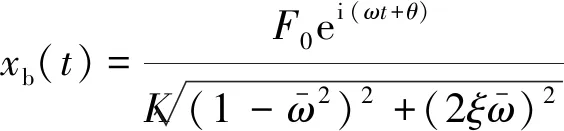
(2)

对式(2)进行傅里叶变换，得到系统幅频特性方程为

(3)

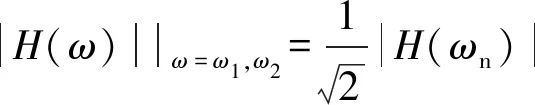
(4)

求解得：

(5)

从而求得阻尼比：

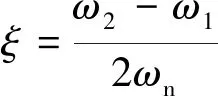
(6)

行波超声电机正常工作时驱动频率不能小于工作模态共振频率，否则电机无法工作，也无法通过测振得到频率小于ωn的幅频曲线。因此，对于超声电机定子模态阻尼比，式(6)可改写为

(7)

1.2 定子振动模态及阻尼比的测试实验

本文利用德国Polytec公司生产的PSV-300扫描式多普勒激光测振系统对TRUM-70H超声电机定子进行模态测试。该系统最大工作频带为1.5 MHz，位移分辨率为100 nm。将电机定子(内圈固支在电机底座上)固定在测试台上，接入电压峰-峰值100 V的正弦激励信号。先进行振动模态测试，再对各个模态共振频率点进行振幅测试，最后在TRUM-70H的工作模态B011共振频率点附近(大于共振频率点)测得定子振幅的频率响应曲线。整个实验环境如图1所示。

图1 PSV-300多普勒激光测振系统

模态扫频测试范围为20～50 kHz，结果显示定子激发出3个较明显的振动模态，分别是B010、B011和B012。对这3个模态进行振幅测试，其结果分别为1.6m、2.0m和1.0m，如图2所示(振幅以B011模态为例)。

图2 TRUM-70H电机定子扫频和B011模态参数

通过图2可以发现，工作模态B011处的频率为36 914 Hz，调节激励信号频率进行采样振幅测试，得到“激振频率-齿面振幅”数据曲线。利用半功率带宽法计算得到ξ为0.802%，如图3所示。

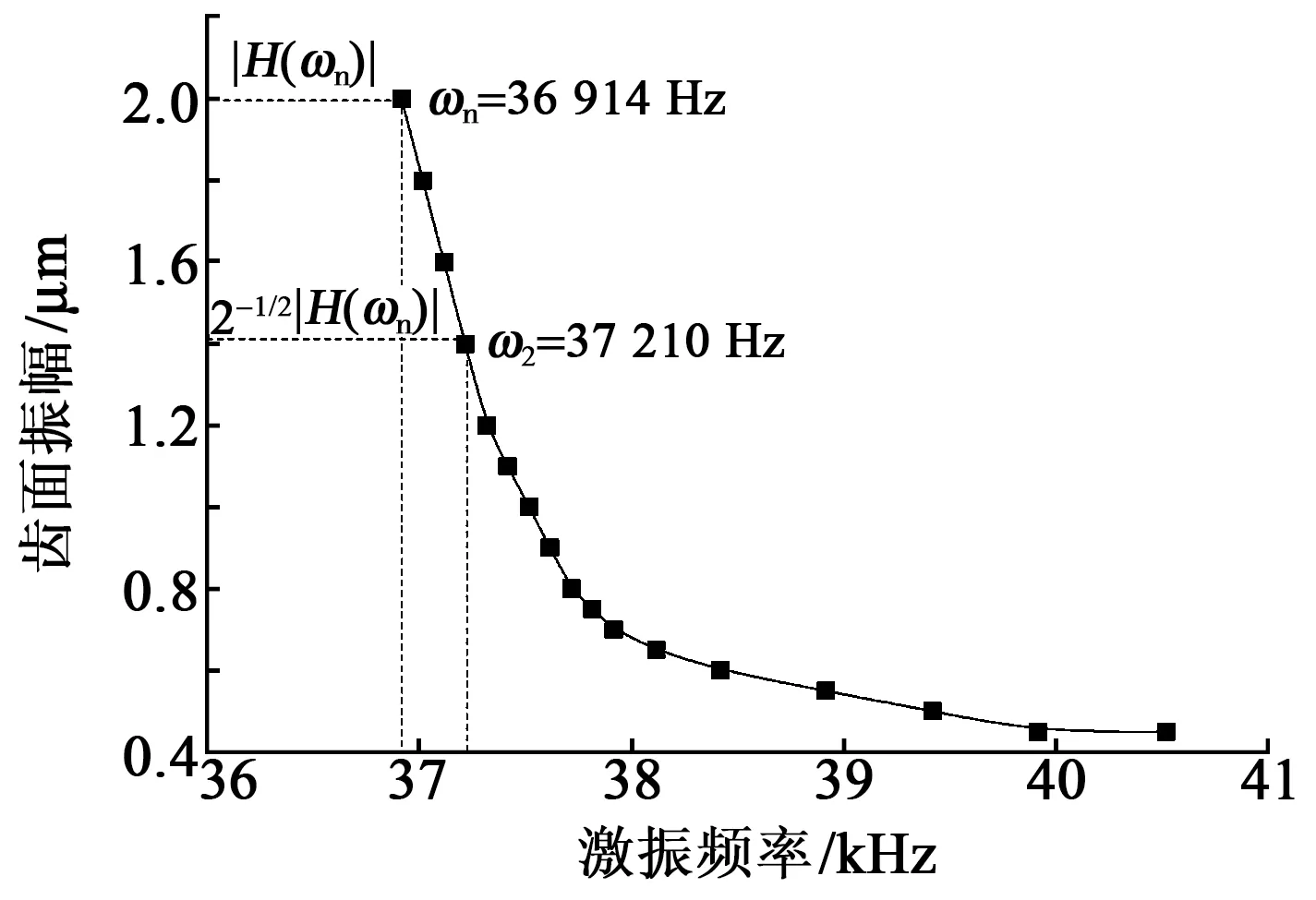
图3 响应振幅和激振频率曲线

2 基于阻尼比的有限元模型验证

2.1 参数化建模及谐响应分析

TRUM-70H电机定子弹性体采用的是磷青铜材料(QSn6.5)，压电陶瓷片材料为PZT-8。确定好材料参数后，在有限元软件ANSYS15.0中进行几何建模和网格划分。网格以六面体单元为主，该模型总共包含4 597个单元和33 773个节点，网格单元平均质量系数为0.75。在几何建模时，将齿高h和齿距w做了参数化处理，以便研究齿特征尺寸参数的变化对定子模态的影响。该定子的齿特征初始参数h=1.5 mm，w=0.8 mm。整体模型如图4所示。

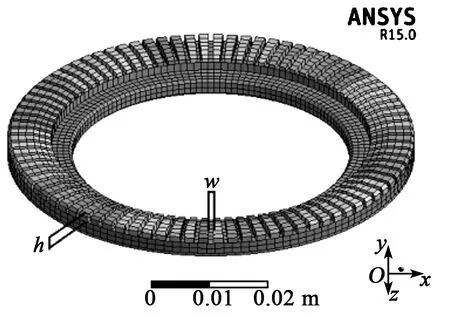
图4 TRUM-70H定子有限元模型

将定子模型内圈固支，设置压电陶瓷电压峰-峰值为100 V，频率为20～50 kHz，阻尼比为0.802%，进行谐响应仿真分析，得到齿面响应振幅(y向)曲线和B011振型如图5所示。假如忽略阻尼比，仿真结果偏差会很大，如表1所示。通过对比发现代入阻尼比时，仿真振幅与实测振幅基本吻合；忽略阻尼比时，仿真振幅比实测振幅高3～4个数量级，结果不可靠。由此可知,虽然定子阻尼比很小，但不可忽略。

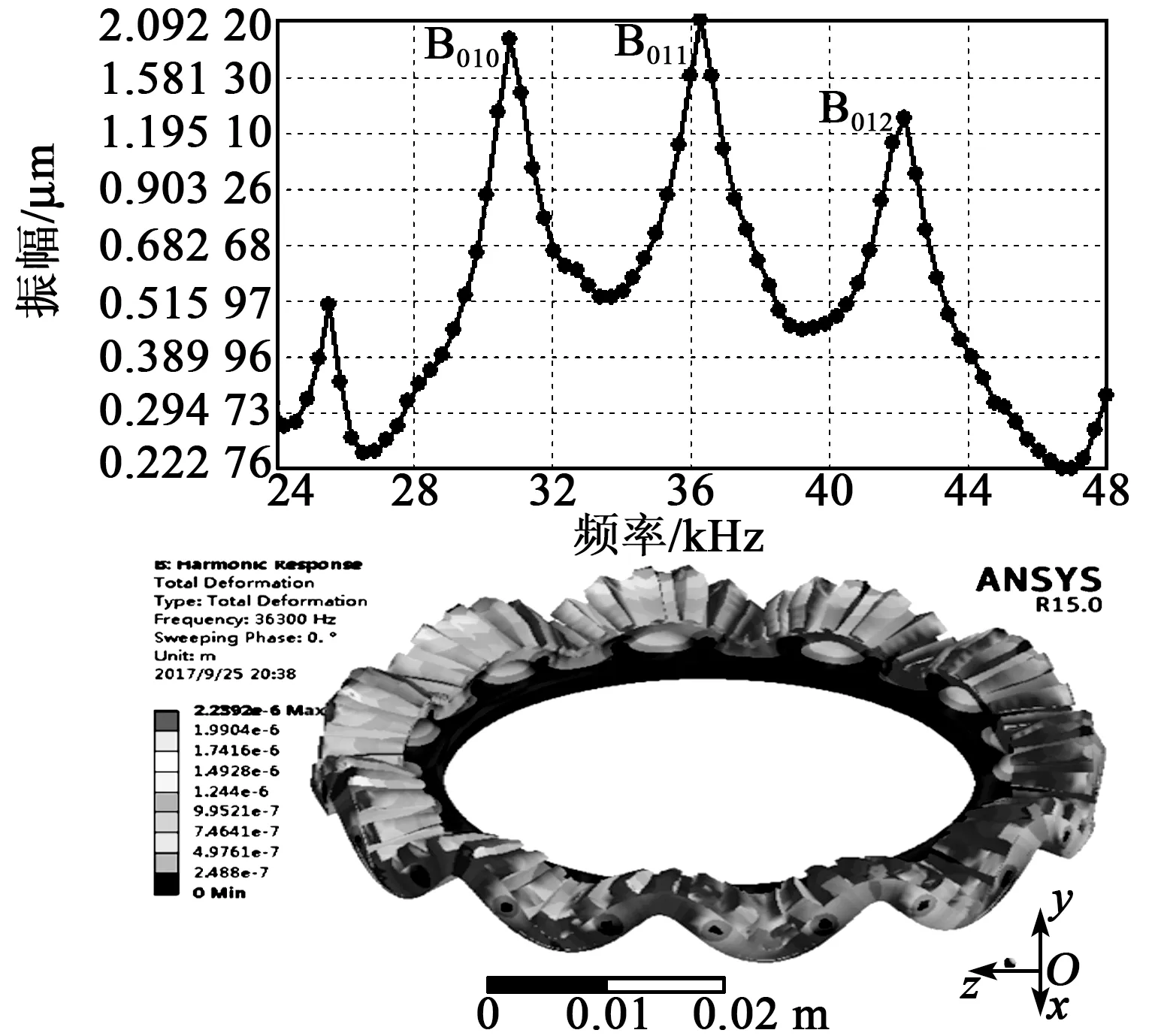
图5 定子谐响应仿真分析的幅频曲线(上)和B011振型(下)

表1 TRUM-70H定子的模态频率及振幅

2.2 齿特征优化及谐响应分析

齿的特征对定子振动模态影响较大，本文希望通过改变齿的尺寸参数，获得一款更低转速、更高输出扭矩的中空行波电机。因此，以w、h作为设计参数，以工作模态B011的频率和齿面振幅为目标参数，进行了输入变量与输出变量的相关性分析[10]，研究w和h对目标模态的影响。结果显示，w对模态频率几乎无影响，h与模态频率近乎成线性关系，h越大，模态频率越低；w和h对振幅均有影响，w越大，h越大，振幅就越大，其中h对振幅的影响比w大，如图6所示。

要使电机获得低转速和大扭矩，转速因子(模态频率与振幅乘积)不能太大，而在定子厚度不变的情况下，齿高对振幅的影响更明显，即对电机转速影响更明显。同样的输出功率下，转速越高，扭矩越小，因此，为了降低转速，新定子的振幅可以略微减小，但振幅不能过低，否则无法驱动转子；要使输出扭矩增大，就要使定子齿与转子的接触面积增大，齿距减小，但考虑到现实加工技术，齿距也不能过小。综合考虑后，取新定子的w=0.5 mm，h=1 mm，并重新进行建模和谐响应分析，得到振幅与频率响应仿真曲线。

3 实物验证

为了验证齿特征参数改变后有限元模型的准确性，本文加工了新定子实物，并组装成新电机TRUM-70HA，如图7所示。新定子的仿真幅频曲线与实物激光扫频结果如图8所示。测振装置的激励电压设置为100 V(峰-峰值)，实际振幅测试数据如表2所示。由表2所见，齿特征参数改变后，定子模态改变，仿真预测的模态频率及振幅与实测结果仍较吻合。对TRUM-70H和TRUM-70HA电机进行了“扭矩-转速”测试实验，测试装置如图9所示。实验结果表明，前者最高空载转速为90 r/min，堵转扭矩为1.0 N·m;后者最高空载转速为63 r/min，堵转扭矩为1.2 N·m。二者的机械特性曲线如图10所示。这说明TRUM-70HA电机符合低速大扭矩的设计目标，定子的有限元模型谐响应分析及齿特征参数的变量关系分析准确地预测了定子振动模态变化，指导了设计参数的选取。

图7 TRUM-70H定子(左)和TRUM-70HA定子(右)

图8 TRUM-70HA定子仿真幅频曲线和激光扫频实测曲线

表2 TRUM-70HA定子的模态频率及振幅

图9 TRUM70系列电机负载特性测试装置

图10 不同电机的机械特性曲线

4 结束语

本文以TRUM70H中空行波电机定子为研究对象，建立了有限元模型并进行谐响应分析，结果发现定子模态阻尼比对模型仿真结果准确性有着重要影响。通过对定子实物的多普勒激光测振分析，利用半功率带宽法测定了B011模态阻尼比，代入模型后得到的定子工作模态B011仿真频率与实测频率误差为1.66%，仿真振幅与实测振幅误差为4.61%，前后两阶模态也基本吻合。通过分析输入与输出参数变量的关系，重新设计了定子齿特征参数，再次进行谐响应分析后加工了定子实物并测振分析，新定子的工作模态B011仿真频率与实测频率误差为0.62%，仿真振幅与实测振幅误差为1.94%，前后两阶模态仍然基本吻合。设计的新定子电机转速降低，堵转扭矩提升，符合预期。结果表明,在准确的阻尼比参数设置下，谐响应仿真分析结果较可靠，有助于提高超声电机定子设计和加工制造结果的可靠性，减少电机设计的主观经验性。