改进的考虑自动驾驶仪动态特性的有限时间滑模导引律
张力丹, 伊国兴
(哈尔滨工业大学 空间控制与惯性技术研究中心,黑龙江 哈尔滨 150001)
0 引 言
导弹的导引规律是制导系统的核心思想,是实现导弹可以追踪目标并达到良好制导精度的理论基础。现代战争中制导精度是导弹打击性能的关键性指标之一,导弹自动驾驶仪的动态延迟特性对制导精度造成的影响是难以忽略的。尤其是导弹在大气层内作战时,所需过载的气动力由侧滑角和攻角产生,这比由直接侧向力来提供需用法向过载的导弹而言对自动驾驶仪的延迟特性会更加敏感。在打击大机动目标时,自动驾驶仪的动态延迟特性将不能保证高的制导精度[1~4]。
传统的导引律设计方法有追踪法、平行接近法、比例导引法等。这些经典导引律的设计都是把自动驾驶仪环节当作一个理想环节,忽略了自动驾驶仪的延迟特性[5~7],在一定程度上会牺牲掉导弹的制导精度。文献[2,8]将自动驾驶仪的动态特性用一阶环节来表示,实际应用中自动驾驶仪是一个具有复杂的高阶动态特性的设备。故在导引律的设计中用更贴近自动驾驶仪延迟特性的二阶环节来表示其动态特性[1,4,5]。在末制导阶段,由于精确制导时间十分短暂,通常只有几秒钟,导引律的设计应保证实现视线角速率在有限时间内快速收敛的指标[1,6,10]。
滑模控制具有响应快、鲁棒性强、物理实现简单等特点,广泛应用于航天控制领域,但由于时空滞后开关及控制系统惯性影响等原因存在抖振的缺陷[11]。为改善系统的抖振现象,Kachroo P设计了一个低通滤波器来使切换面函数变得平滑,有效改善了系统的抖振程度;Vicente P V采用边界层设计法设计了饱和函数来替代原控制函数中的开关函数;张天平学者则考虑利用模糊逻辑的方法来使控制函数连续化;学者李琳提出采用神经网络来设计滑模面。高为炳提出的趋近律概念可通过适当调整趋近律式中的参数来有效削弱抖振,具有设计简单可操作性强的特点,故在滑模控制中采用趋近律的方式来改善抖振现象[8,9]。
本文对导弹的纵向平面进行分析,设计基于滑模变结构的综合考虑自动驾驶仪的动态特性和有限时间收敛的新型导引律,使导弹满足更高的制导精度。
1 弹目制导模型的建立
这里考虑轴对称寻的导弹的制导模型,导弹的纵向平面和侧向平面的分析是相似的,故在这里只做导弹纵向平面的导引律分析,同理可将该导引律的设计思路应用到侧向平面。
将导弹和目标定义为两个运动质点,分析导弹和目标在平面内相对运动关系,图1为纵向平面拦截示意图。
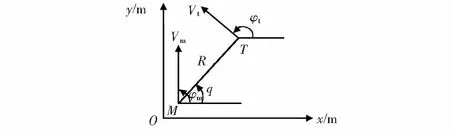
图1 弹目相对运动关系
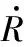
由图1可得出以下弹目相对运动方程

(1)
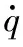
(2)
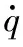
(3)
(4)
式中wR,uR分别为目标和导弹加速度在视线方向上的分量,wq,uq分别为目标和导弹加速度垂直于视线方向上的分量。
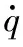
(5)
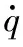
用二阶动态环节来近似逼近导弹自动驾驶仪的实际高阶动态特性
(6)
式中ζ和ωn分别为导弹自动驾驶仪的阻尼比和自振频率,u为导弹自动驾驶仪输入的加速度指令,aM为自动驾驶仪输出给导弹的加速度指令。
在式(6)中考虑到导弹模型的气动参数偏差会造成不确定性误差,这里用Δ来表示,则可得纵向平面内考虑导弹自动驾驶仪二阶动态特性的制导模型
(7)
在制导模型式(7)中含有目标机动加速度,它一般是难以准确估计的,导弹模型也存在不确定性,但目标机动加速度和导弹模型的不确定性通常是有界的。因此,将这两部分看作是建模误差。假设|aT|<ε和|Δ|<ρ(ε和ρ均为正常数)来对式(7)进行变换。
定义状态变量
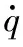
(8)
对x1关于时间求导可得
=x2+Δ1
(9)
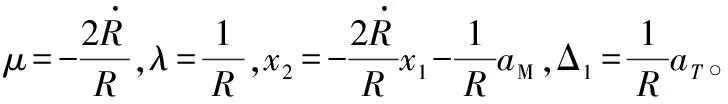
对x2关于时间求导可得
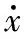
(10)
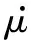
对x3关于时间求导可得

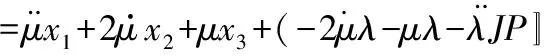

(11)
=a1x1+a2x2+a3x3+bu+Δ3
(12)
故变换后的考虑导弹自动驾驶仪二阶动态特性的制导模型式为
(13)
2 导引律的设计与分析
2.1 设计滑模面
考虑到滑模控制的优越性,在这里采用滑模控制的方式来设计导弹的新型导引律。
首先定义滑模面
S=C1x1+C2x2+C3x3
(14)
式中Ci均为不为零的常数。
抖振是滑模控制的最大缺陷,为尽量削弱抖振对制导系统的影响,采用指数趋近律来改善滑模到达过程的品质[13]。指数趋近律的表达式如式(15)
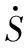
(15)
通过适当调整参数k和ε来保证趋近切换面的时间和运动点到达切换面时的速度的指标达到最优。
对滑模面S关于时间求导
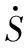
C3bu+C1Δ1+C2Δ2+C3Δ3
(16)
根据式(15)和式(16),设计导引律为
u=-(C3b)-1[C3a1x1+(C1+C3a2)x2+
(C2+C3a3)x3+KSp/q+ρsgnS]
(17)
K为正常数,q和p为正奇数,且q 将设计的导引律式(17)代入式(16),可得 (18) 前面已经假设目标机动加速度和导弹模型的不确定性有界,所以令 |C1Δ1+C2Δ2+C3Δ3|≤ρ (19) 选取Lyapunov函数 (20) 对上式时间求导,得 ≤-KSp/q+1-ρ|S|+|S||C1Δ1+C2Δ2+C3Δ3| ≤-KSp/q+1=-K(2V)(p/q+1)/2 =-2(p/q+1)/2KV(p/q+1)/2 (21) 根据文献[2]中对非线性系统有限时间稳定定理的阐述可知,制导系统状态将在tr内到达滑模面,然后继续在滑模面上运动直到状态收敛为零。该制导系统有限时间稳定 (22) 设计的导引律中含有符号函数项,这是一个非连续的开关函数,容易造成制导系统的抖动[13]。为了消弱抖动,需要用一个连续函数来代替这个非连续函数。由双曲正切函数的曲线图。可知tanh(x)在定义域-π 改进后的考虑自动驾驶仪动态特性的有限时间导引律为 (23) 式中δ为一个正常数,仿真中,δ=0.1。 参考相关文献资料设计的导引律中各参数值分别为C1=60,C2=15,C3=1,q/p=7/9,K=3,ρ=0.1;导弹的可用过载加速度为40gn,gn为重力加速度。根据导弹设计的要求和实际工程经验,选取导弹自动驾驶仪动态参数为ζ=0.6,ωn=8 rad/s,导弹模型不确定性为Δ=5 %um/s2。这里分别对导弹进行非机动、常值机动和正弦机动三种情况的仿真分析。弹目初始条件值设置如表1所示。 表1 仿真所需参数初始值 图2所示是目标非机动时的导引律仿真图。 图2 导引律曲线 由图2可以看出在0.5 s后原始设计的导引律出现抖振,而改进后的导引律曲线平滑并能很好地代替原来设计的导引律。 这里采用经典的比例导引律与改进的新型导引律进行对比。比例导引律的表达式为 (24) 式中K为比例系数, 通常取值为2~6[7],这里选取K为4。 用ADFTCG表示所设计的考虑自动驾驶仪动态特性的有限时间导引律,PNG表示比例导引律。关于导弹不机动、在纵向平面进行20 m/s2的常值机动及在纵向平面进行aT=50sin(2πt/0.5)m/s2的正弦机动的脱靶量结果如表2所示。 表2 三种机动情形下的脱靶量 三种机动情形下视线角速率变化如图3(a)、图4(a)、图5(a),加速度指令仿真如图3(b)、图4(b)、图5(b)。 图3 目标非机动仿真 图4 目标常值机动仿真 图5 目标正弦机动仿真 由仿真结果图3~图5可看出:设计的导引律能使制导系统在有限时间收敛。经计算得到制导时间为2.278 1 s。由图3~图5可看到:考虑了导弹自动驾驶仪动态特性的导引律可以更加迅速地响应目标的机动变化,两种导引律的视线角速率均接近零,直到制导即将结束才有发散。在制导快结束时比例导引律的视线角速率比新型导引律先发散,这也是造成它脱靶量更大的原因。结合脱靶量的结果来看,设计的新型导引律具有更高的制导精度。 考虑到制导末段的时间有限,参考滑模控制理论和有限时间稳定定理在导弹的纵向平面设计了一种基于滑模控制的考虑导弹自动驾驶仪动态特性的有限时间收敛导引律。同时为减弱滑模控制造成的抖振采用双曲正切函数改进了导引律。仿真结果表明设计的新型导引律曲线平滑,可以使导弹在有限时间内迅速跟踪上目标运动,有效补偿了自动驾驶仪的延迟特性。设计新型导引律极大提高了导弹的制导精度,更贴合现代战争中对导弹打击性能的要求。2.2 稳定性分析
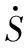

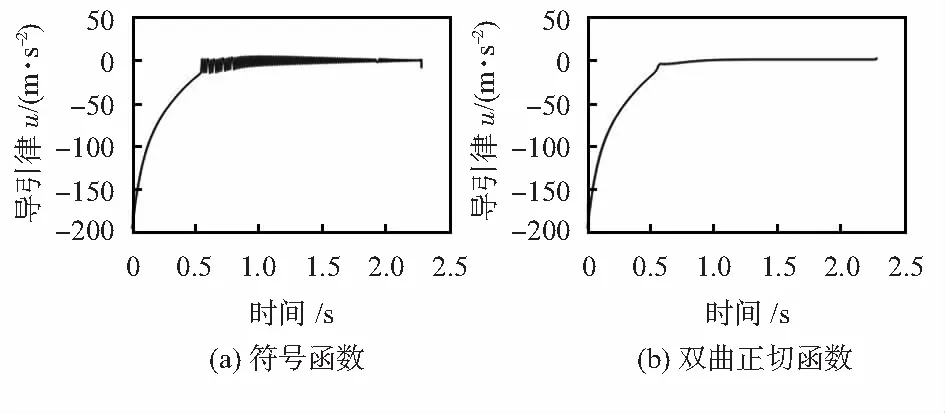
2.3 导引律的改进
3 仿真验证





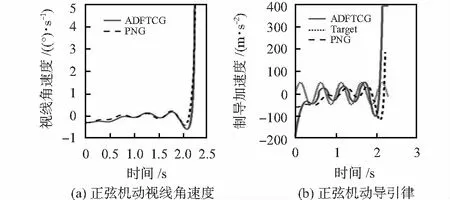
4 结 论

