手机信令数据识别职住地的时空因素及其影响

钮心毅，谢 琛

(同济大学建筑与城市规划学院，高密度人居环境生态与节能教育部重点实验室，上海 200092)

0 引言

近年来，手机信令数据在城市交通、城市规划等领域引起了广泛关注，也已经在各大城市的交通调查、城市交通规划、城市总体规划中得到了较多实际应用[1-6]。基于手机信令数据可以识别居民的居住地、工作地，从而获取通勤OD、揭示职住空间关系。这是手机信令数据辅助交通调查、城市交通规划、城市总体规划的基础性工作[7-11]。

手机信令数据是手机用户在移动通信网络中留下的时空轨迹数据，只是记录了居民日常行为的时空轨迹。使用手机信令数据识别居住地、工作地的基本原理是对手机用户长时间时空轨迹规律进行测算，以多日夜间的时空轨迹推算居住地、以多日日间的时空轨迹推算工作地。职住地算法是采用某种规则对居住、工作行为的时间、空间特征进行归纳。如果采用不同的规则、同一规则中采用不同的参数取值，可能导致识别结果的差异。这种差异是否会对职住地结果可靠性产生影响是一个值得研究的议题。已有文献更关注手机信令数据职住地识别结果的应用，极少有对职住地算法本身的讨论，也缺少不同算法对识别结果可靠性影响的讨论。

本文首先讨论手机信令数据的特征，总结识别职住地的若干关键因素。之后，依据关键因素组合成若干种算法，以多种组合方法分别对同一城市的同一批手机信令数据进行职住地识别，分析不同规则对职住地识别结果的影响程度。

1 基于手机信令数据测算职住地的关键时空因素

基于手机信令数据测算职住地是对工作、居住行为一般规律的时空特征进行测算，涉及三个时空因素。

1.1 时间连续性

因为信令是由用户的位置移动、通话、上网等行为激发，所以对单个用户而言，信令在时间上虽然比较连续，但是相邻记录的时间间隔却不是固定的。即使在持续开机情况下，相邻记录之间间隔可能长于1 h，也可能短到在1 min 内产生数十条记录。时间连续性是职住地识别的首要时空因素。

应对时间连续性的问题，已有文献中提出过若干方法和设想[12-16]。综合相关研究与自身实践，本文将其归纳为4种时间规则。

1）累积时间法。

累积时间法的思路是通过累积用户每日在各个位置的停留时间，以日间最长停留时间位置为工作地、以夜间最长停留时间位置为居住地。累积时间法是通过计算累积时间来消除信令记录时间间隔不规律的影响。

2）特征时间法。

特征时间法的思路是以特定的时间间隔(如1～2 h)测算用户在特定时间点所停留基站的位置，然后选择出重复次数最高的基站或者多个停留基站的中心位置。日间特征时间点选择出的位置作为工作地，夜间特征时间点选择出的位置作为居住地。

3）信息熵法。

信息熵法是将熵的概念引入职住地计算[16]。通过计算用户在每个基站位置停留的信息熵大小，消除信令记录时间间隔不规律的影响。

当用户在夜间共停留n个位置U1,U2,U3, …,Un，其对应的概率为每个位置停留时间占总时间的比例，再通过信息熵公式计算得到用户的信息熵，即

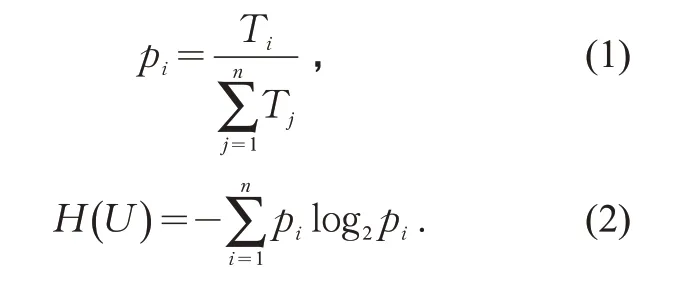
式中：pi为每个停留位置的停留时间占总时间的比例/%；Ti，Tj为每个停留位置的停留时间/s；H(U)为该用户的信息熵值。

信息熵反映了对象活动强度。信息熵越小，说明个体时空活动越稳定；信息熵越大，说明个体时空活动越频繁。分别将用户的日间、夜间信息熵小于一定阈值的停留位置作为工作地和居住地。

4）时间阈值法。

测算用户夜间合计停留时间超过夜间总时间一定比例阈值的基站，若连续观测周期中该基站每日被重复识别出的次数大于某个阈值天数，则将其识别为居住地[16]。使用同样方法对日间用户停留位置进行比较，识别出用户的工作地[7]。

1.2 空间位置分辨率

信令记录以移动通信基站位置定位。信令记录中表示的基站位置与用户实际所在位置之间可能存在数十米到数百米的差异。每一条信令记录中信令发生时的基站可能是距用户最近的基站，也可能仅是相邻基站之一。由于移动通信网络的特点，用户实际位置发生移动时，所连接的基站可能不变；也可能出现用户实际位置并未移动时，所连接基站发生变化。由此导致空间位置分辨率问题，即职住地识别的第二个时空因素。

空间位置分辨率会对1.1 节中4 种时间规则测算造成影响，以累积时间法为例，会使得真正居住地(工作地)基站的停留时间变短，导致最后未能达到居住地(工作地)识别时长要求。应对空间位置分辨率问题，一般采用某种空间聚合方法，将一定距离范围内基站均视为同一个基站。只要用户信令记录都在A基站周边特定距离内的基站上，均视为没有离开A基站。这个距离数值就是空间聚合距离值。空间聚合距离值过大、过小均会对居住地(工作地)识别带来影响。仍以累积时间法为例，聚合距离值过大，会使得用户发生了实际出行但仍被视为停留在A 基站，夸大了在A基站的停留时间；聚合距离值过小会使得其失去应有的作用，仍会影响到A基站的停留时间。

1.3 数据时间序列长度

由于用户个人行为规律会有偶然性变化，需要有一段连续日期对用户行为进行测算，才能确定居住地、工作地。如果连续测算日期过短，也许会导致识别的居住地、工作地错误。因此，数据时间序列长度是职住地识别需要应对的第三个时空因素。

数据时间序列长度影响对用户行为的重复性判断。较短周期可能将居民偶然几天行为判断为长期规律性行为。同时，由于数据质量原因也使得数据时间序列长度更为重要。因为多种原因会导致一段日期中可能有若干日数据质量较差无法使用，更长的数据时间序列会确保数据有效日期数量。实际工作中，会出现难以获取连续若干周数据的情况(例如仅有1～2 周)，较短的数据时间序列会对识别结果造成多大影响还需要进行比较。

2 基础数据及分析框架

2.1 基础数据概况

本文使用江西省南昌市的中国联通匿名手机信令数据开展研究，数据时间为2015年4月7日—5月17日，连续41天。其中，4月7日、5月2日信令记录总数、用户总数过低，数据质量较差，予以排除。其余日期的每日信令记录总数、每日出现用户ID 总数均比较一致，平均每天约有70 万用户产生约4185 万条记录，每个用户平均每天产生约60条信令记录。连续5周的数据时间序列中也排除五一休假的日期，只保留5 周中工作日，为此保留其余27个工作日。

2015年该市基站分布如图1所示，基站之间平均距离1 068 m。每日均选取在市域内累计停留时间大于2 h 的用户，排除过境用户；进一步将其中信令记录出现日期占总天数60%及以上的用户视为活跃用户，得到活跃用户543 389 人，占该市常住人口的9.94%。

2.2 三类因素的实验组合

为比较时间连续性、空间位置分辨率、数据时间序列长度各自影响程度，分别对三类因素进行两两比较，控制第三类因素不变。同时尽可能保证使用相同参数来控制变量，排除参数取值对结果的影响。三类因素组合得到33组算法(见图2)。

实验中使用的4种时间规则均将20:00—次日5:00作为居住地识别时段，9:00—16:00作为工作地识别时段。

图1 基站分布Fig.1 Distribution of base station

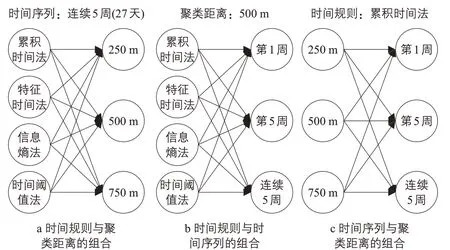
图2 三类因素的实验组合Fig.2 Experiment with the combination of three types of factors

累积时间法中，分别将20:00—次日5:00和9:00—16:00 两个时段累积总停留时间最长的位置作为该用户居住地、工作地，且保证至少有60%的天数在该位置停留超过2 h。

特征时间法中，分别将20:00—次日5:00和9:00—16:00 每隔一个整点小时的时间点为居住地、工作地识别的时间点。以至少有60%时间点在同一个位置识别出当日居住地、工作地。汇总每日识别的居住地和工作地，将识别天数大于总天数60%的位置作为该用户的居住地和工作地。

信息熵法中，在20:00—次日5:00和9:00—16:00，分别以用户在整个时段内平均停留3个位置作为该用户活动稳定的上限判断标准，即信息熵大致为1.5。识别信息熵小于1.5 的用户，将由累积时间法得到的最长停留位置作为其居住地和工作地。

时间阈值法中，将20:00—次日5:00 停留时间占总时间的比例大于60%的停留位置作为当日的居住地，再统计研究天数内不同位置被识别的总天数，将识别总天数大于总天数60%的位置作为该用户识别居住地。用同样方法，在9:00—16:00进行工作地识别。

选择3种空间聚合距离，分别为250 m，500 m 和750 m；三种数据时间序列，包括第 1 周(4月 13—17日 5 个工作日)、第 5 周(5月11—15日5个工作日)、连续5周(4月8日—5月15日27个工作日)。

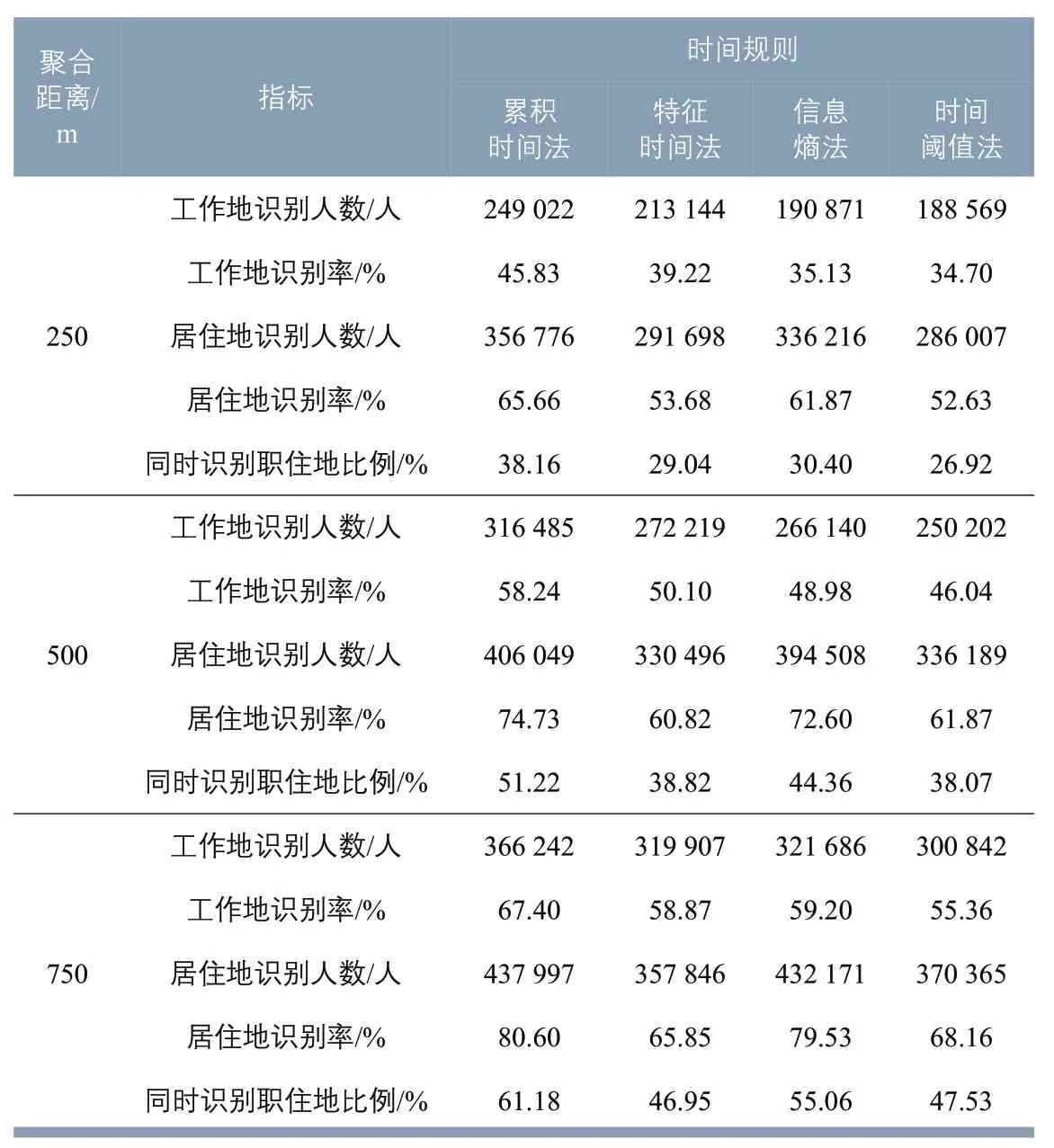
表1 时间规则与聚合距离组合的识别率Tab.1 Identification rate with the combination of time rule and aggregated distance

在保证数据时间序列均为连续5 周的条件下，以前述4种时间规则以及250 m，500 m和750 m 3 种聚合距离组合成12 组算法，比较不同时间规则、聚合距离对职住地识别结果的影响。

在空间聚合距离均为500 m 的条件下，对前述4 种时间规则以及第1 周、第5 周、连续5 周3 种数据时间序列组合成12 组算法，比较不同时间方法、不同数据时间序列长度对识别结果的影响。

在时间规则均采用累积时间法的条件下，对250 m，500 m 和750 m 3 种空间聚合距离以及第1周、第5周、连续5周3种数据时间序列组合为9 组算法，比较不同聚合距离、不同数据时间序列对职住地识别结果的影响。

2.3 结果的可靠性比较

可靠性比较的最佳方法是将职住地识别结果与人口普查、经济普查、交通调查的结果进行对照。当前最常用的检验方法是居住地分布与人口普查、工作地分布与经济普查的就业岗位分布进行相关性检验。实际情况下，往往是由于没有交通调查数据，才需要进行手机信令辅助测算，所以很难对信令数据测算的通勤距离等结果的可靠性进行检验。

本文采用各组结果相互之间进行一致性比较的方法，比较不同时间规则、空间聚合距离、数据时间序列对识别结果的影响程度。通过识别率、平均直线通勤距离①、共同识别用户一致性3 个指标来确定影响的敏感程度。

识别率指居住地、工作地识别出的人数与活跃用户数之间的比值。各种方法都需要保证一定的识别率。虽然识别率高低并不能代表结果的可靠性，但如果某个因素变化导致识别率显著变化，说明该类因素取值对结果有显著影响。

平均直线通勤距离指同一组合算法中同时识别出了职住地且职住地位置不在同一个基站的用户，其直线通勤距离的平均值。如果因素改变引起平均直线通勤距离变化较大，说明该因素对识别结果的可靠性有显著影响。

共同识别用户一致性用以比较多种组合的共同识别用户职住地空间位置的一致性，通过同一用户在不同组合算法中识别出位置的平均距离差和共同识别用户位置一致率表示。当两种组合比较时，共同识别用户位置一致率=位置一致用户数量/职住地空间位置识别人数相对较少组合的总人数×100%。

3 结果比较

3.1 时间规则与聚合距离

3.1.1 识别率

保持连续5 周数据时间序列不变，活跃用户为543 389人。4种时间规则算法和3种聚合距离的12个组合结果识别率见表1。在同一聚合距离下，累积时间法识别率明显高于其他方法；在同一时间规则下，随着聚合距离增加，识别率均明显上升，在250～500 m上升幅度最大。

3.1.2 平均直线通勤距离

计算上述12 个组合结果的平均直线通勤距离(见表2)。随着聚合距离增大，平均直线通勤距离大幅度下降，说明直线通勤距离对聚合距离取值有较大敏感性。尤其当使用特征时间法和时间阈值法时，平均直线通勤距离对聚合距离取值敏感性更为显著。在同一聚合距离下，不同时间规则得到的平均直线通勤距离不同，累积时间法得到的值最大。

3.1.3 共同识别用户一致性

将12 个组合结果相比较(见图3a 和图3b)，特征时间法与其他3个时间规则位置的平均距离差最大，其次是时间阈值法。累积时间法和信息熵法无差距，这是因为信息熵法本身是基于累积时间进行熵值计算。在共同识别用户位置一致率上，时间阈值法与其他3个规则的重合率最低。

以同样的方式比较聚合距离影响(见图3c 和图3d)，各个方法之间位置的平均距离差均在20 m以内，差异不明显。3种聚合距离下，共同识别用户位置一致率均在96%以上。

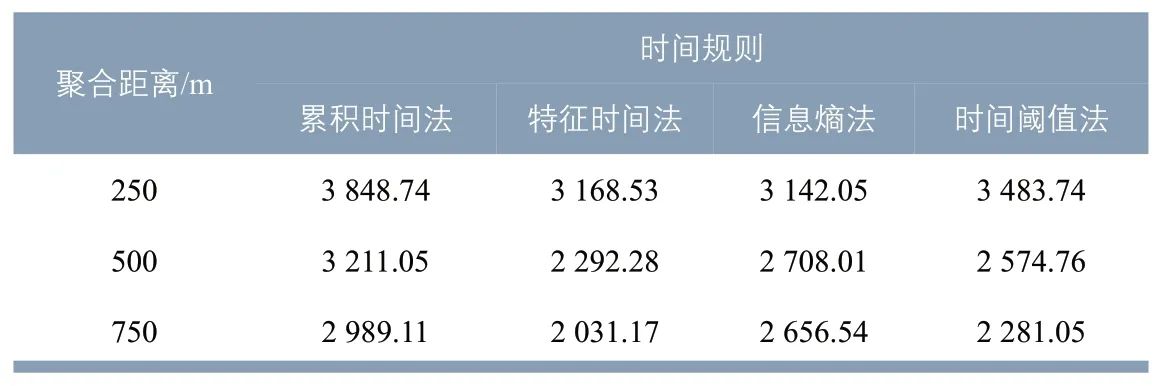
表2 时间规则与聚合距离组合的平均直线通勤距离Tab.2 Average linear commuting distance with the combination of time rule and aggregated distance m

图3 时间规则与聚合距离组合下位置的平均距离差及位置一致率Fig.3 Average distance difference and position consistency rate with the combination of time rule and aggregated distance

从共同识别用户一致性来看，时间规则算法带来的差异相对较为明显；聚合距离取值带来的差异不明显。

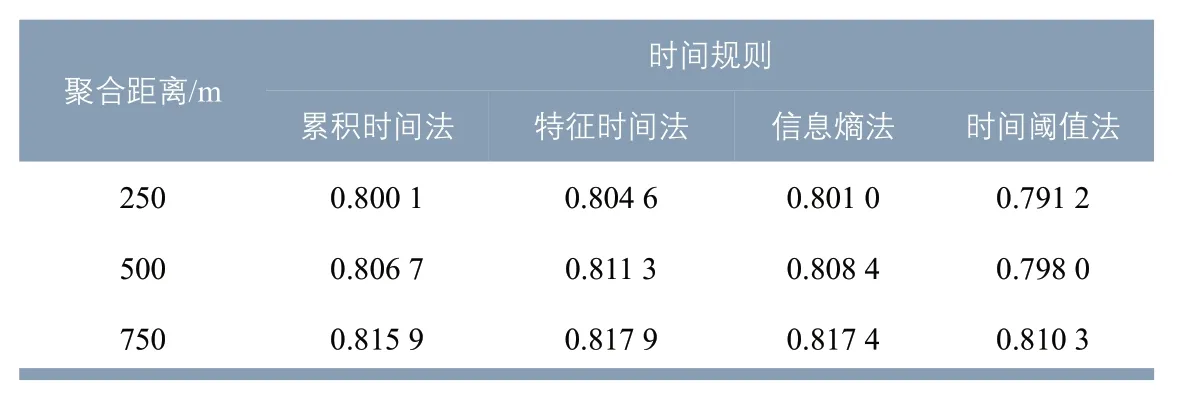
表3 时间规则与聚合距离组合结果与“六普”常住人口的相关系数Tab.3 Correlation coefficient between the result from the combination of time rules and aggregated distance and the 6th national population census

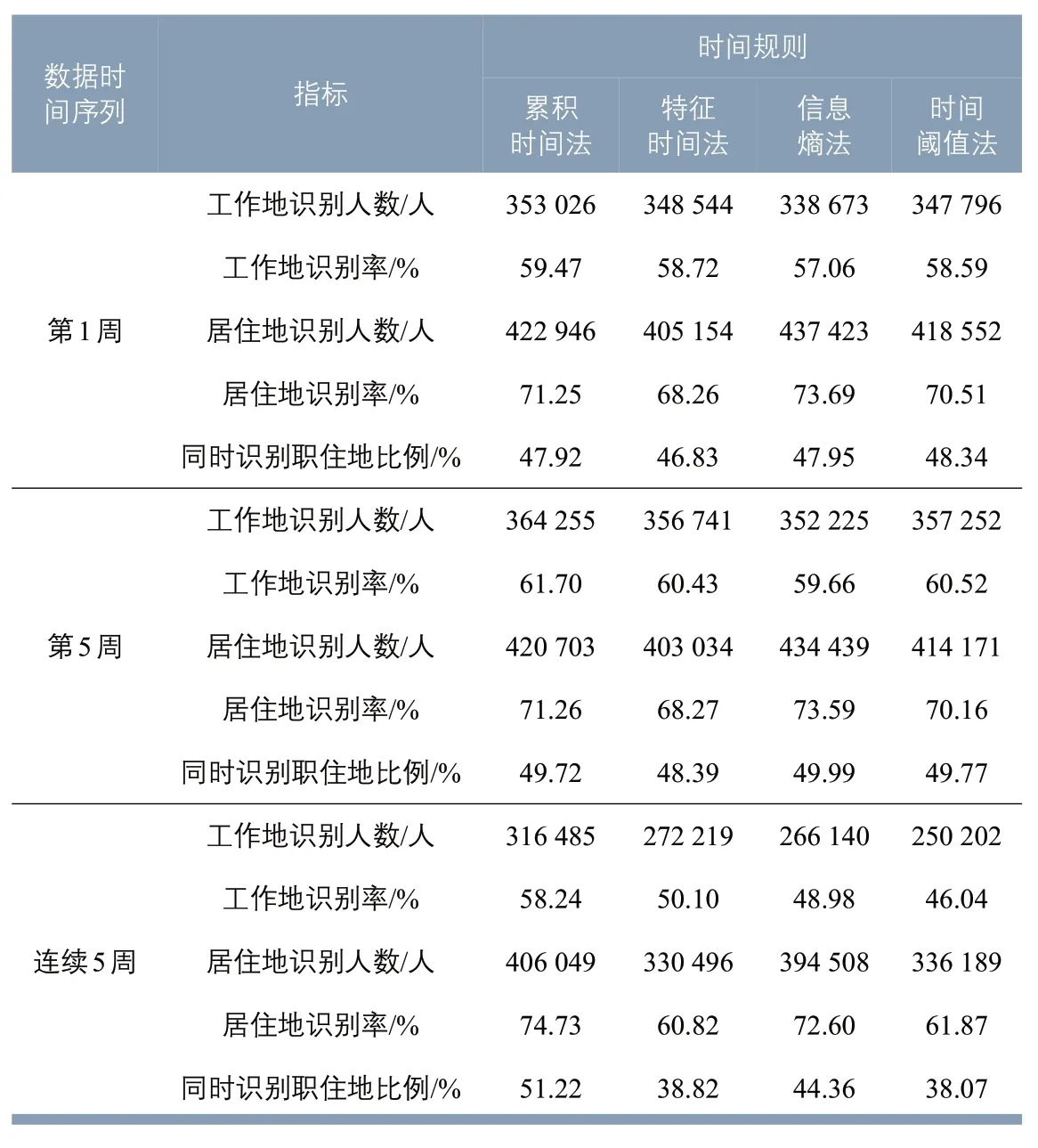
表4 数据时间序列与时间规则组合的识别率Tab.4 Identification rate with the combination of data time series and time rules

表5 时间规则与数据时间序列组合的平均直线通勤距离Tab.5 Average linear commuting distance with the combination of time rules and data time series m

3.1.4 与人口普查数据的相关性检验

使用当前最常用的结果检验方法，将测算得到的居住地分布与人口普查数据进行相关性检验。以街道(镇)为空间单元，12组算法与“六普”常住人口数量的相关系数见表3。虽然结果之间存在较明显的差异，但是所有组合得出的相关系数均在0.8 左右，与人口普查数据的相关性检验均呈现强相关。

3.2 时间规则与数据时间序列

3.2.1 识别率

统一取值空间聚合距离为500 m。第一周内活跃人数593 587 人，第5 周内活跃人数590 348人，连续5周活跃人数543 389人。4 种时间规则与3 种数据时间序列的12 个组合的职住地识别结果见表4。第1周与第5周的4 种时间规则识别率相近，连续5 周的4种时间规则识别率有显著差异。连续1 周与连续5 周相比，特征时间法、时间阈值法识别率显著下降，说明二者对数据时间序列变化更加敏感。

3.2.2 平均直线通勤距离

12 个组合的平均直线通勤距离见表5。4种时间规则下，第1周与第5周的平均直线通勤距离均较为接近，但与连续5 周结果有一定差异。其中，特征时间法和时间阈值法得出的平均直线通勤距离值随着数据时间序列的不同变化更加显著。

3.2.3 共同识别用户一致性

如图4a和图4b所示，3种数据时间序列下，各种方法的共同识别用户平均距离差为150～550 m，差异也较为明显。其中，第1周与第5 周的结果差异最大。数据时间序列变化使得识别结果之间差异较大，3 种数据时间序列下，位置一致率仅为78%～87%。

以同样的方式比较时间规则影响，如图4c 和图4d 所示，总体上各个方法之间的平均距离差均在60 m以内，差异并不明显。4种时间规则下共同识别用户位置一致率均在84%以上，说明结果差异相对不明显。其中，特征时间法与其他方法的共同识别用户位置一致率相差最大。

从共同识别用户一致性来看，3 种数据时间序列带来的差异较为明显；4 种时间规则下各个方法所得结果的一致性好于数据时间序列。

3.2.4 与人口普查数据的相关性检验

以街道(镇)为空间单元，将12组算法识别的居住人数分别与“六普”常住人口数量进行相关性分析，得到相关系数(见表6)。12组算法的结果之间虽存在较明显差异，但相关系数均在0.8 左右，说明居住地识别结果与人口普查数据的相关性检验均呈现强相关。

3.3 聚合距离与数据时间序列

3.3.1 识别率

统一采用累积时间法，3 种聚合距离与3 种数据时间序列的9 种组合的识别率结果见表7。在同一聚合距离下，连续5 周的工作地、居住地识别率与一周的识别率略有变化。在同一数据时间序列下，随着聚合距离增大，职住地的识别率明显增大。可见，聚合距离对识别率的影响大于数据时间序列带来的影响。

3.3.2 平均直线通勤距离

9 个组合结果的平均直线通勤距离见表8。随着聚合距离增大，平均直线通勤距离明显下降。3 种数据时间序列对平均直线通勤距离值的影响并不明显。

3.3.3 共同识别用户一致性

对9 个组合的结果进行比较(见图5a 和图5b)，各种方法共同识别用户位置的平均距离差较大，为97～491 m，第1 周与第5 周的结果差异最大。3 种数据时间序列下，共同识别用户位置一致率为82%～94%。如图5c 和图5d 所示，三种聚合距离下，各个组合方法之间共同识别用户位置的平均距离差都接近0，共同识别用户位置一致率达到99.9%以上，说明不同聚合距离对结果的影响较小，共同识别用户一致性较好。因此，数据时间序列的日期(第1周、第5周)与时间序列的长度共同影响着识别结果。

3.3.4 与人口普查数据的相关性检验

以街道(镇)为空间单元，将9 组算法识别的居住人数分别与“六普”常住人口数量进行相关性分析，得到相关系数(见表9)。9组算法的结果之间虽存在较明显差异，但相关系数均在0.8 左右，说明居住地识别结果也均与人口普查数据呈现强相关。

4 实际应用中需要注意的问题

4.1 数据源

本文使用了中国联通的匿名信令数据，活跃用户数量占该城市常住人口数量的9.94%。由于使用同一批信令数据对多种不同规则组合识别结果进行比较，在实验设计上，数据自身的用户数量和占该城市的比例均不会影响比较结果。但在实践中如果采用不同运营商的数据源，由于各家运营商用户普及率不同、基站密度也不同，可能会影响职住地的测算结果。这种因素的影响程度需要进一步研究。

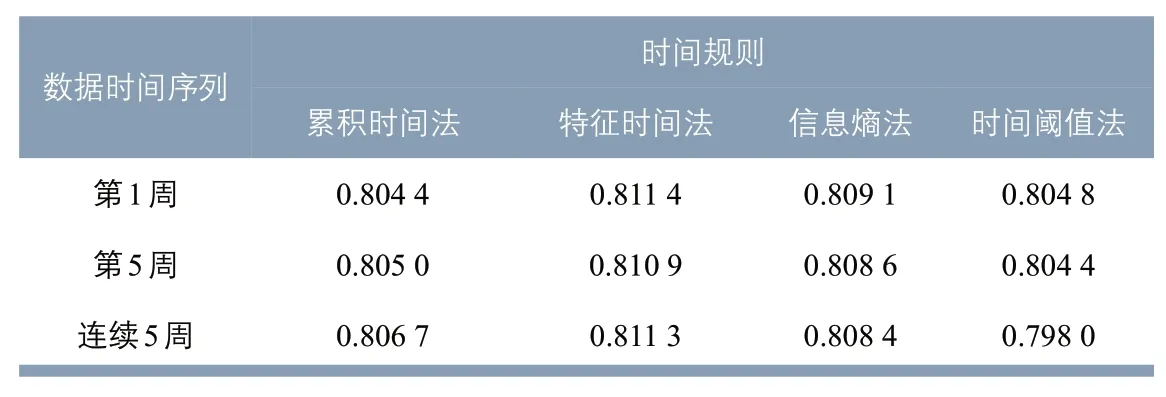
表6 时间规则与数据时间序列组合结果与“六普”常住人口的相关系数Tab.6 Correlation coefficient between the result from the combination of time rules and data time series and the 6th national population census

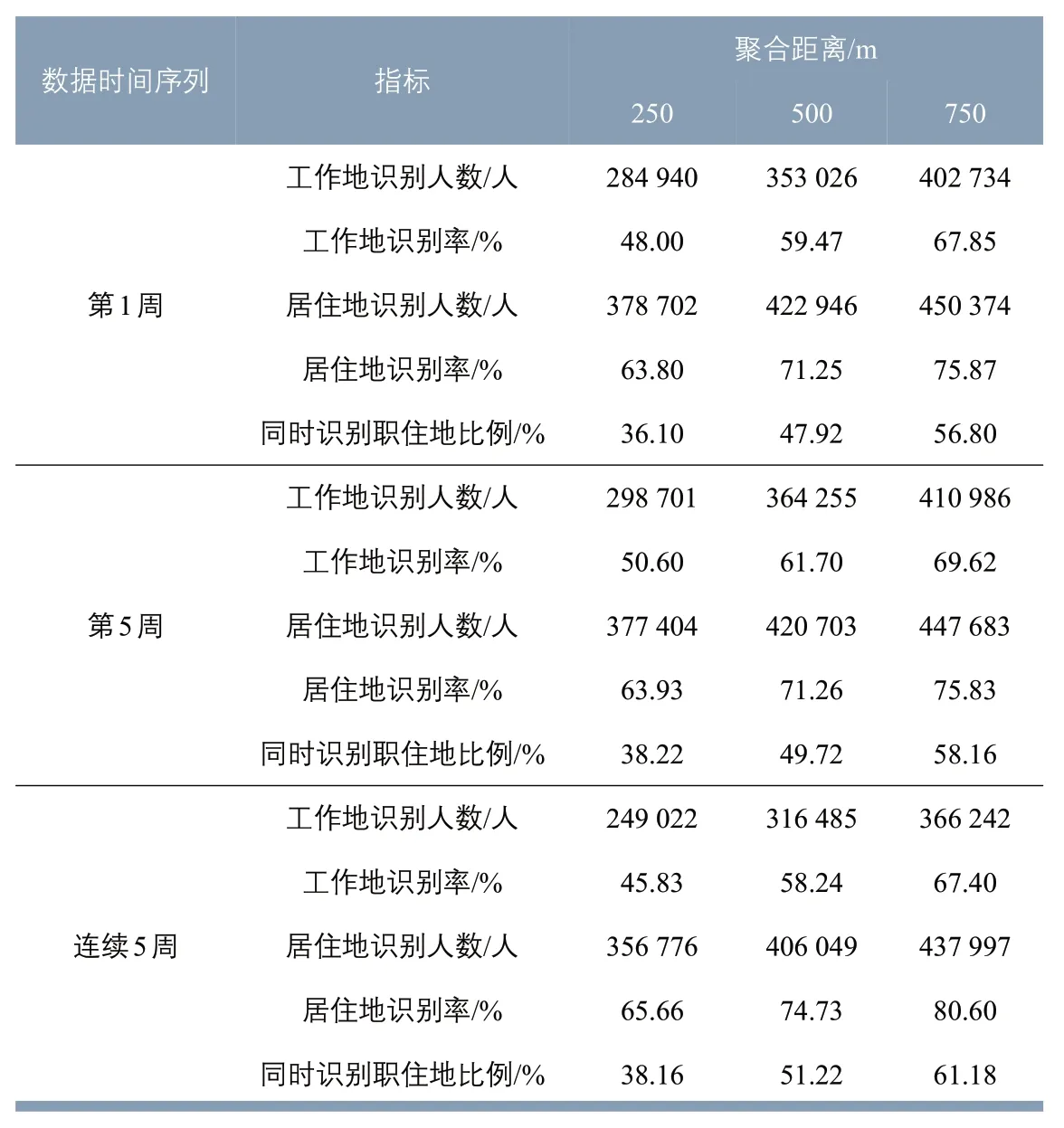
表7 聚合距离与数据时间序列组合识别率Tab.7 Identification rate with the combination of aggregated distance and data time series

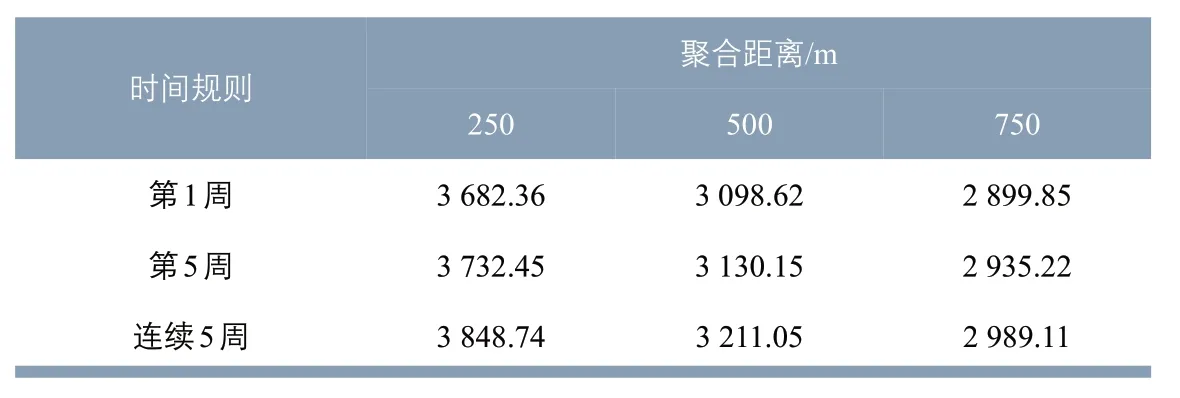
表8 数据时间序列与聚合距离组合的平均直线通勤距离Tab.8 Linear commuting distance with the combination of data time series and aggregated distance m

4.2 重复率

4种时间规则都涉及重复率，本文统一采用了60%的重复率值。显然较高的重复率值将导致识别率下降，但高重复率约束下职住地识别结果的准确率可能也会提高。由于重复率对职住地测算结果的影响趋势已经有了共识，本文未对重复率取值进行敏感性比较。因居住、工作行为存在一定不规律性，一般情况下50%～60%的重复率取值是适宜的。在实际工作中，确定了时间规则、空间聚合距离、数据时间序列后，仍需要对重复率取值进行敏感性检测，确定该城市适宜的重复率值。

4.3 聚合距离变化对平均直线通勤距离的影响

空间聚合距离增大会导致平均直线通勤距离明显变小。不同聚合距离取值下，共同识别用户一致性均较高，聚合距离扩大未改变共同识别用户的职住地，导致通勤距离减小的原因来源于没有被共同识别的用户，即较大聚合距离下多识别的那部分用户的平均直线通勤距离。在实验中，以时间规则和聚合距离组合，对500 m 和250 m 取值的结果进行比较，500 m 取值新增识别者的平均直线通勤距离仅为2 266 m，远小于两者共同识别人群的平均值3 849 m。在较大聚合距离下，许多日间活动位置不太固定、在相近基站活动的居民被识别出工作地，而这部分人被识别出的居住地、工作地的距离明显偏小。随着聚合距离增大，工作地识别率上升幅度明显高于居住地识别率上升幅度(见表1)，这也能在一定程度说明上述情况。

这一结果说明，追求过高的识别率并无意义，反而可能对职住地测算的结果准确性产生负面影响。这些被扩大出来的用户真实行为目的需要今后进一步研究证实。

4.4 可靠性检验

当前已有的职住地测算方法是基于对居民一般居住、工作行为规律认识，建立在固定居住地和工作地并且有规律的夜间居住时段、日间工作时段前提下。显然，部分居民可能没有固定的工作地(如交通运输业的职业驾驶人等)，也有可能上夜班，居住、工作时间恰好相反。这些居民行为可能是不同因素对识别结果造成影响的原因之一。

本文发现，多种时间规则、空间聚合距离、数据时间序列对职住地识别结果有显著影响。由于无法获取南昌市居民出行调查数据，尚不能精确地判断哪一种组合方法与居民实际通勤情况最为接近。实际交通规划工作中常常将手机信令数据测算职住地作为一种辅助调查手段使用，往往在缺少居民出行调查情况下进行或是与居民出行调查同步进行。缺少居民出行调查数据是实际工作中的常见情形。为此，要采用多种方法组合，进行多组结果相互比较、选择一致性较好的组合方式。这种工作方式更加符合交通规划实践的场景。倘若有接近时段的居民出行调查数据，应将平均直线通勤距离等与实际调查值对照，验证规则和参数选取的可靠性。

本研究也说明了当使用手机信令数据计算职住地时，算法本身还存在若干值得关注的未知因素。手机信令数据表征的居民出行特征还不能用过于简单的规则全部挖掘出来。

5 结论

5.1 时空因素对职住地识别的影响

3个时空因素对职住地识别结果都有不可忽视的影响。对于平均直线通勤距离，聚合距离取值对结果影响最大，数据时间序列对结果影响最小。对于共同识别用户一致性，数据时间序列对结果的影响最大，聚合距离对结果影响最小。对于识别率，聚合距离对结果的影响最大，时间规则和数据时间序列对结果影响较小。

1）时间规则的影响。

特征时间法得到的平均直线通勤距离明显小于其他3 种时间规则；时间阈值法识别率稍低，信息熵法实质上是在累积时间法上叠加了更严格的约束条件，结果导致平均直线通勤距离变小。在共同识别用户一致性上，时间阈值法与其他3个规则的重合率最低。

2）空间聚合距离的影响。

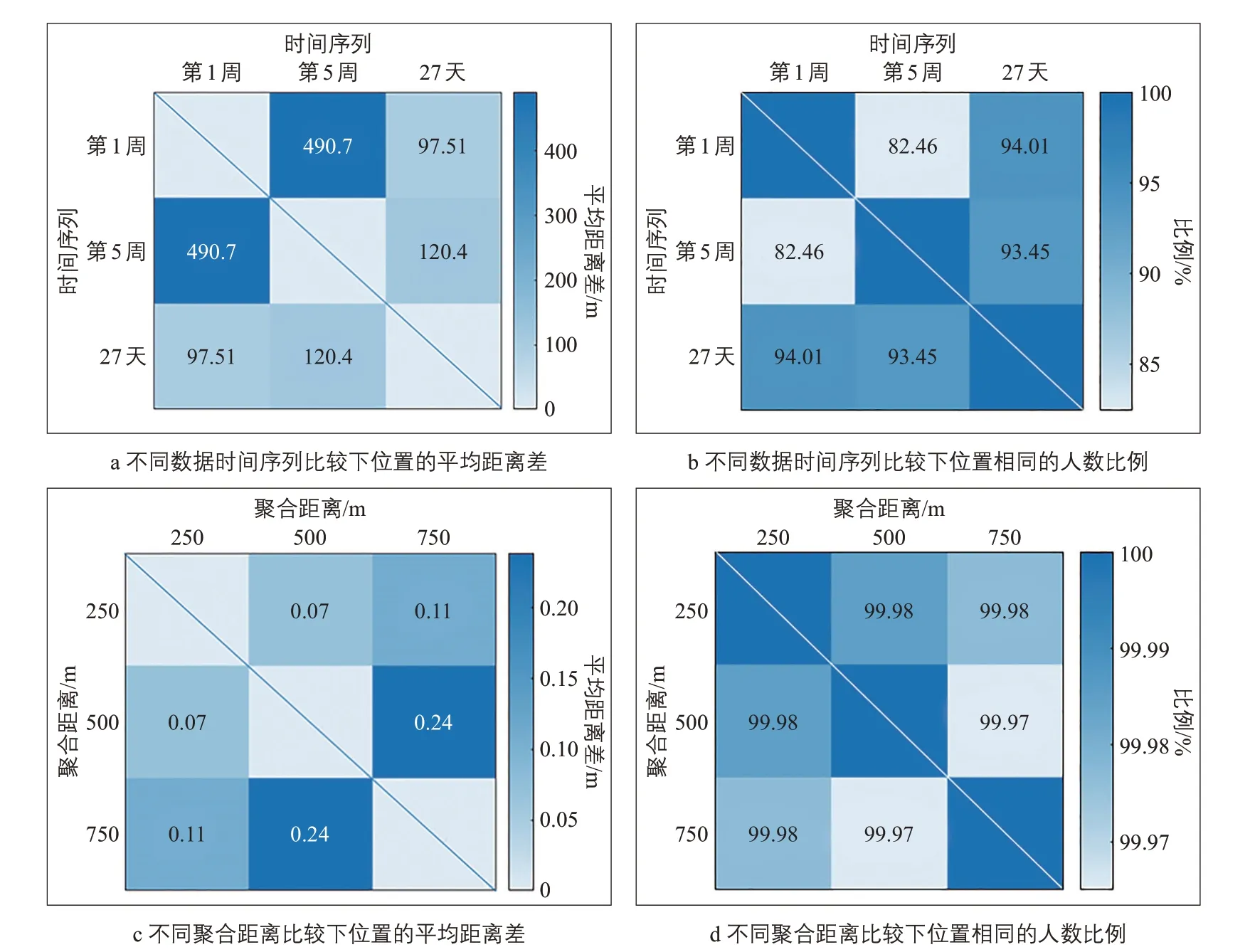
图5 数据时间序列与聚合距离组合下位置的平均距离差及位置一致率Fig.5 Average distance difference and position consistency rate with the combination of data time series and aggregated distance

平均直线通勤距离对聚合距离取值非常敏感。较大空间聚合距离取值虽然使识别率上升，但是使平均直线通勤距离明显变小。聚合距离扩大未改变共同识别用户的职住地，而是纳入了更多行为位置不固定的用户，这些用户的行为可能不是居住、工作目的。

3）数据时间序列的影响。

数据时间序列1 周与5 周、不同的一周相互之间共同识别用户一致性差异明显。不同数据时间序列之间共同识别用户位置一致率不高；不同的一周，共同识别用户的职住地位置平均距离差超过500 m。1 周是较短的数据时间序列长度，对职住地测算结果可靠性产生明显影响，且不同周的结果也有显著差异。

5.2 对职住地识别结果可靠性检验的建议

由于规则选取会对结果产生显著影响，手机信令数据职住地识别结果必须经过可靠性检验。当前常用方法是与人口普查、经济普查进行空间分布比对。针对本文33 种组合的居住地测算结果，采用街道(镇)空间单元与“六普”常住人口数量分布进行相关性检验，结果都显示了强相关。这表明仅用普查数据验证空间分布是不够的，仍无法准确判断结果可靠性。

实际工作中往往是在没有居民出行调查的前提下才使用手机信令数据测算职住地，本文建议增加平均直线通勤距离、共同识别用户一致性两种检验方式。应采用多种因素、多种取值组合进行测算，对照比较多组识别结果，选取一致性较好的组合方式。多个组合、多个取值对照比较是一种数据训练的方法，一旦规则和参数确定，后续同一来源数据可以用同一套规则和参数取值。

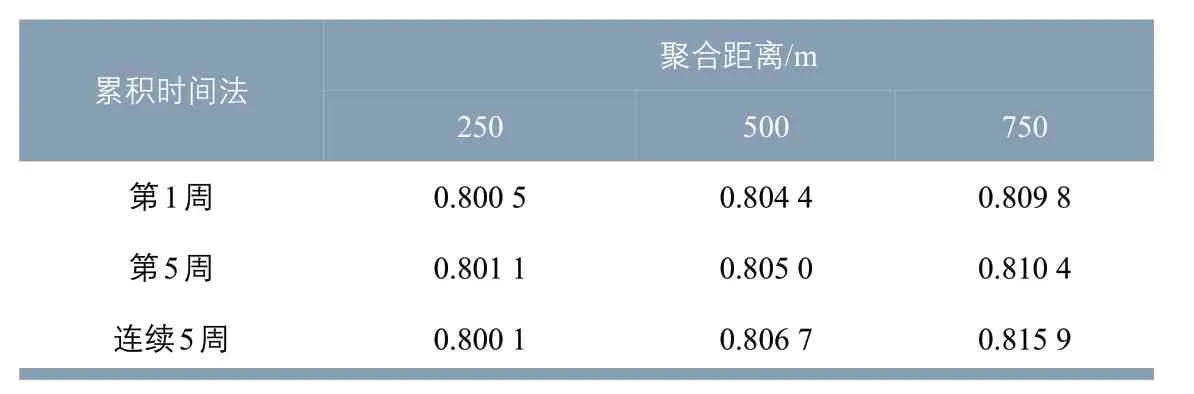
表9 数据时间序列与聚合距离组合结果与“六普”常住人口的相关系数Tab.9 Correlation coefficient between the result from the combination of data time series and aggregated distance and the 6th national population census

5.3 对职住地识别时空因素规则选取与适用性的建议

对手机信令数据识别职住地的规则选取和参数选择提出三点建议：1)在时间连续性规则中，应慎重使用特征时间法。累积时间法、时间阈值法是相对较好的时间规则，一般情况下建议优先考虑。2)应慎重选取空间聚合距离值。在没有居民出行调查获取居民直线通勤距离值对照验证的情况下，建议优先使用较小的空间聚合距离值。3)在职住地测算中应使用较长的数据时间序列，不能使用过短的数据时间序列。如果能在一年不同季节选择较长数据时间序列进行较连续测算，会使得结果更为可靠。

注释：

Notes：

①手机信令数据测算得到的通勤距离是代表居住地的基站与代表工作地的基站之间的直线距离。这一距离值比真实通勤距离短，本文称其为直线通勤距离。