基于Lyapunov稳定性理论的单轨迹车辆运动稳定性分析

韩忠磊，段 薇，周 涛，胡三宝

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，湖北 武汉 430070；3.武汉船舶通信研究所，湖北 武汉 430079)

单轨迹车辆有两个显著的振荡模态，weave和wobble模态。Wobble模态产生于转向自由度，低速时更易发生，表现为转向摇晃；weave模态包含了转向、侧翻、横摆和侧向自由度，高速时更易发生，表现为迂回穿行。Sharp在1971年研究了关于摩托车直线行驶稳定性的问题[1]，辨识出了非振荡模态capsize模态及振荡模态weave和wobble模态。之后Sharp论证了车架柔性对摩托车高速weave模态的影响[2]，柔性车架通过后轮与车身之间的线性弹簧-阻尼器来表征。Sharp还讨论了摩托车轮胎动态特性不同假设下车辆weave模态和wobble模态的频率响应[3]。Rajput等利用牛顿-欧拉法建立了较为简单的单轨迹车辆模型[4-5]，对影响车辆行驶稳定性的转向器阻尼、车辆质心位置等参数进行了根轨迹的图解分析。文献[6]研究了车辆稳态回转时设计参数和道路摩擦对稳定性的影响。文献[7]研究了单轨迹车辆模态辨识方法。

对于单轨迹车辆的稳定性分析一般是将模型线性化，考虑侧向和纵向运动解耦，在不同车速下进行根轨迹分析。多数文献指出，capsize模态即车辆的侧倾模态是最重要的模态，因为它表征了单轨迹车辆侧翻倒地自由度的稳定性，当capsize模态不稳定时，分析weave及wobble模态已然失去意义。而车辆设计参数、行驶工况、轮胎模型对capsize模态稳定性定量分析的研究较少。为了定量分析车辆参数对稳定性的影响，以齐次坐标推导了单轨迹车辆的9自由度动力学模型DOF9-BIKE，利用Lyapunov稳定性理论计算了单轨迹车辆直线行驶稳态运动稳定性的条件。

1 单轨迹车辆建模

单轨迹车辆模型包括：前、后轮，前、后总成，前非簧质量。前、后总成通过转向器连接在一起。模型的9个自由度分别为：后总成质心3个方向的移动，车架的横摆、俯仰和侧倾运动，转向运动以及前、后轮的回转运动。如图1所示。

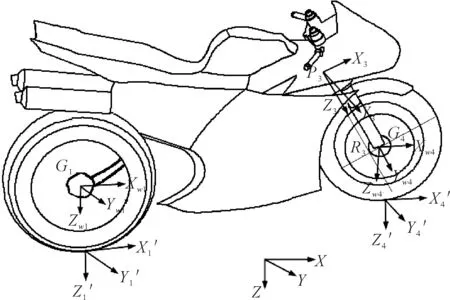
图1 单轨迹车辆DOF9-BIKE模型

1.1 多体动力学模型

全局坐标系的方向如图1所示。由于齐次坐标矩阵对于空间刚体的位置和姿态描述较为简便，计算方便，这里把5个部件各分配一个齐次坐标矩阵Ti：Ti={ui,wi,vi,Gi},i=1,2,…，5。前3个列向量为方向向量，分别为绕X、Y、Z旋转的余弦矩阵，第4个列向量为平移向量，表示位置。

前总成坐标矩阵为T3，局部坐标系原点为X2Y2平面与转向轴的交点P3={x3,y3,z3,1}T。X3Z3平面平行于前轮回转平面，X3轴垂直于转向轴向前，方向向量为u3={ux3,uy3,uz3,0}T；Y3轴平行于前轮轴，方向向量为w3={wx4,wy4,wz4,0}T；Z3轴方向向量为v3={vx3,vy3,vz3,0}T。

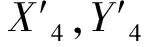
前非簧质量坐标矩阵为T5，局部坐标系原点利用齐次坐标变换为G5=T4{Gx5,Gy5,Gz5,1}T，其中Gx5,Gy5,Gz5为前非簧质量质心在前轮局部坐标系下的位置。方向向量为：u5=u3,w5=w4,v5=v3。

整个建模用到n=33个广义坐标，包括G1,P3,G4位置坐标，各方向向量，以及与轮胎旋转相关的广义坐标θ1,θ4。则广义坐标向量为：

q={x1,y1,z1,sx1,sy1,wy1,wz1,vx1,vy1,x3,y3,

z3,ux3,uy3,uz3,vy3,sx4,sy4,wy4,wz4,vx4,

vz1,vz3,vz4,x4,y4,z4,vy4,θ1,θ4,wx1,vx3,wx4}T

其约束方程为:

φj=0,j=1,2，…，g

其中g=n-9。

由于方向向量均为单位向量，则有：

φ1=|s1|-1φ2=|w1|-1φ3=|v1|-1

φ4=|s4|-1φ5=|w4|-1φ6=|v4|-1

φ7=|u3|-1φ8=|v3|-1

由图1所示，满足正交关系的向量应有：

φ9=s1·w1φ10=s1·v1φ11=v1·w1

φ12=s4·w4φ13=s4·v4φ14=v4·w4

φ15=u3·w4φ16=v3·w4φ17=u3·v3

φ18=w1·v3

向量G1P3垂直于平面Y3Z3，长度为l13，有：φ19=G1P3·w1,φ20=G1P3·v1,φ21=|G1P3|-l13。

图1中，点R3=G4-lRu3必须在转向系坐标Z3轴上，P3R3长度为l34，则有：

φ22=P3R3·w4,φ23=P3R3·u3,

φ24=|P3R3|-l34

1.2 轮胎模型

1.3 拉格朗日方程

带约束的拉格朗日方程如下：

(1)

式中：K为系统动能；λj为拉格朗日乘子;Qi为广义力。

式(1)可利用增广法将其转化为常微分方程，并通过Baumgarte稳定化方法可得到动力学方程如下[8-10]：

2 稳定性理论模型

研究单轨迹车辆在直线行驶时的稳定性问题实际上是研究其稳态运动的稳定性。为了研究的方便，将系统方程化为Воронец方程形式[11]。

(2)

(σ=1,2,…,ε)

(3)

(4)

(5)

(α=k+1,k+2,…,ε;ρ=1,2,…,m-ε;

τ,ν,σ=1,2,…,ε;β=1,2,…,g)

式中，L,F分别为系统拉格朗日函数和耗散力，上述条件意味着约束条件后面(n-m)个是Чаплытин约束(方程不显含坐标但有其速度，且速度被消去，则消去后可独立于约束方程进行研究)，剩下为一般形式的约束。坐标qα(α=k+1,k+2,…,ε)为循环坐标。此外还假设

(α,τ,δ=k+1,k+2,…,ε;ρ=1,2，…,m-ε)

(6)

第一组条件意味着，对循环速度没有耗散；第二、三组意味着确保稳态运动流形存在，其维数不小于循环坐标和非完整约束数目之和。可以证明，在所指条件下，系统运动方程有解：

(7)

(α=k+1,k+2,…,ε)

(8)

式中，wij，uij,vij为系统方程泰勒展开后的系数项，式(8)显然有(m-k)个零根，其余2k个根满足式(9)。由Лялунов-Малкин定理成立有：在满足式(4)～式(6)的非完整系统稳态运动的邻域内，受扰运动特征方程的全部根λ除了(m-k)个外都在左半平面，那么稳态运动是稳定的(但非渐进稳定)。

(9)

3 模型验证及稳定性分析

3.1 模型验证

为验证DOF9-BIKE模型的正确性，将模型在工况1下的仿真结果与BIKESIM结果进行对比。工况1设置为：2～4 s，驱动力矩150 N·m；5～7 s，侧倾角为10°；7～10 s，侧倾角为12°。其中侧倾角利用PID反馈控制转向力矩实现。仿真结果对比如图2～图6所示。

图2 纵向速度对比

图3 转向力矩对比

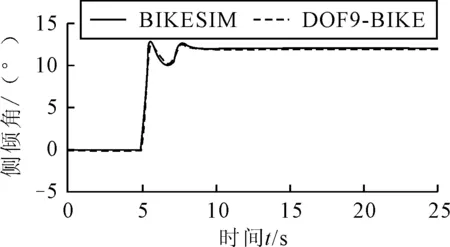
图4 侧倾角对比

图5 后轮垂向力对比

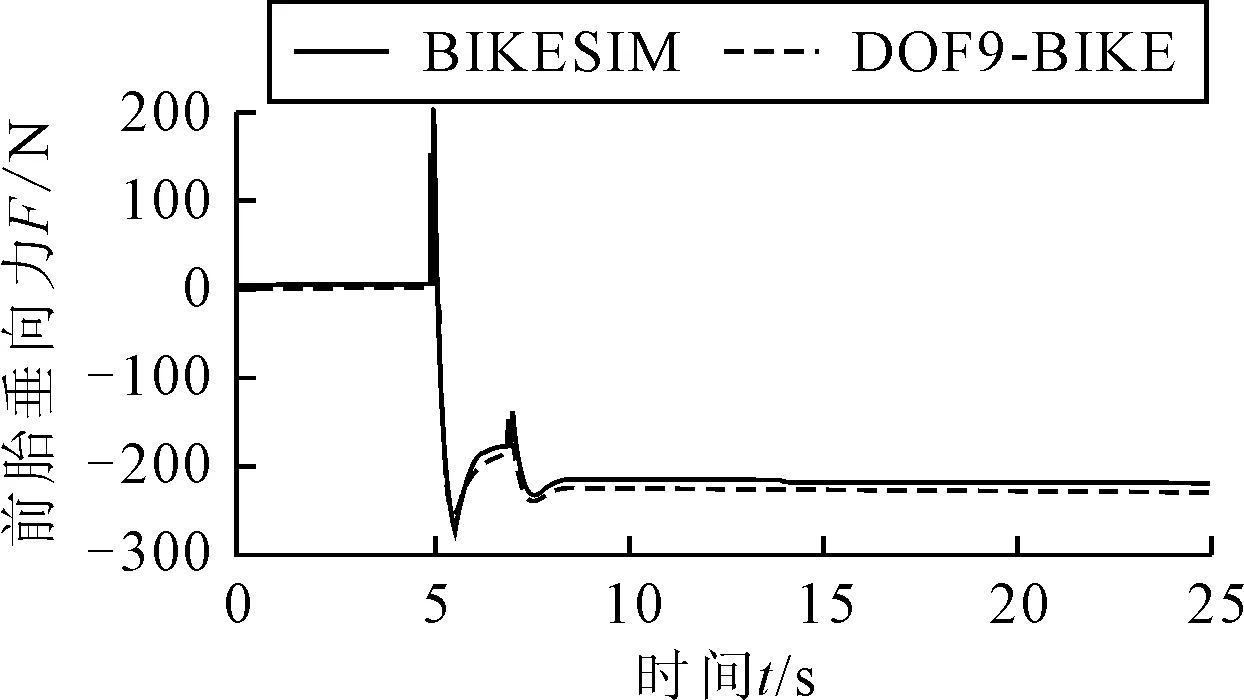
图6 前轮侧向力对比

两种模型从静平衡状态开始施加后轮驱动力，由于DOF9-BIKE模型未考虑悬架，在骤加速和停止加速时，轮胎垂向力对比有明显差别，但在完成加速后，轮胎垂向力大致相等。由于侧倾角为反馈控制，故仿真结果基本吻合。BIKESIM模型从直线行驶状态过渡到回转状态时，在悬架作用下，轮胎侧向力较小，则车辆侧向速度较小，即其纵向速度对比较大，故稳态回转所需转向力矩较小。由图2～图6可知，模型DOF9-BIKE和BIKESIM仿真结果曲线趋势一致，且基本吻合，两者结果的偏差是由车辆动态运动过程中悬架作用导致的。且考虑计算误差，说明了所建立DOF9-BIKE模型的正确性。

3.2 稳态运动的稳定性

分析DOF9-BIKE模型，有满足式(4)～式(6)的稳态解：

qi={wx1,vx3,z4,vy4,wx4}

qρ为除广义坐标x1,y1,x3,y3外剩下的20个广义坐标。将所建立模型DOF9-BIKE转化为第2节所述形式，并得到系统特征方程式(9)。计算得到单变量下单轨迹车辆稳态运动稳定性条件，如表1所示。

表1 车辆稳定的单变量条件

为了验证条件计算的正确性，在BIKESIM中改变车辆参数，在工况2下进行仿真验证。工况2设置为：施加驱动力矩使车辆到达一定速度，9～10 s施加10 N·m转向力矩。这里主要是研究单轨迹车辆受扰动的倾覆问题，故这里仅列出侧倾角受扰变化曲线，如图7～图11所示。

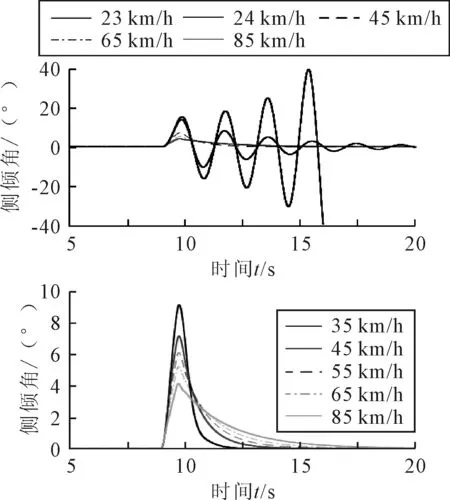
图7 纵向速度对干扰下的侧倾角影响

由图7可知，车速小于24 km/h时，施加干扰转向力矩，车辆侧倾角振荡发散，终使车辆侧倾倒地。当车速大于24 km/h，车辆受扰后能够自动回正到侧倾角为零的行驶状态，车辆的稳态运动是稳定的。车速增大会使扰动侧倾角减小但回复时间增加。

由图8可知，转向器阻尼在0.04～3 Nms/(°)范围内可使车辆稳态运动稳定。3 Nms/(°)的阻尼在实车上是不会出现的，这里仅验证条件计算的正确性。同样，阻尼增大会使扰动侧倾角减小但回复时间增加。

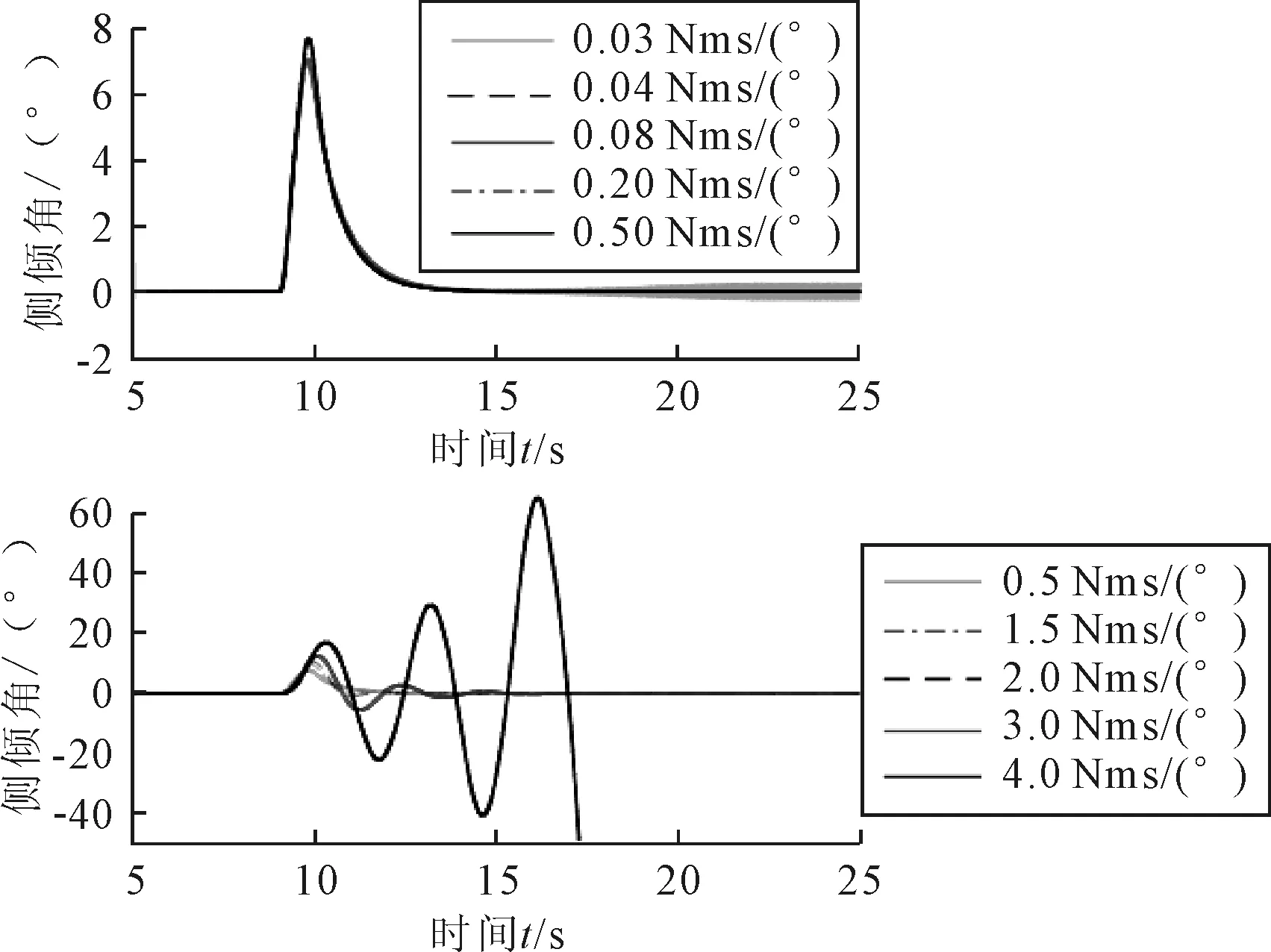
图8 转向器阻尼对干扰的下侧倾角影响

图9为轮胎侧倾刚度对车辆稳定性的影响。这里侧倾刚度是指由侧倾角产生的轮胎回正力矩。当侧倾刚度在0.1～4 Nm/(°)范围内时车辆稳态运动是稳定的。适当增加侧倾刚度不仅可以减小侧倾角扰动，且可减小回复时间。

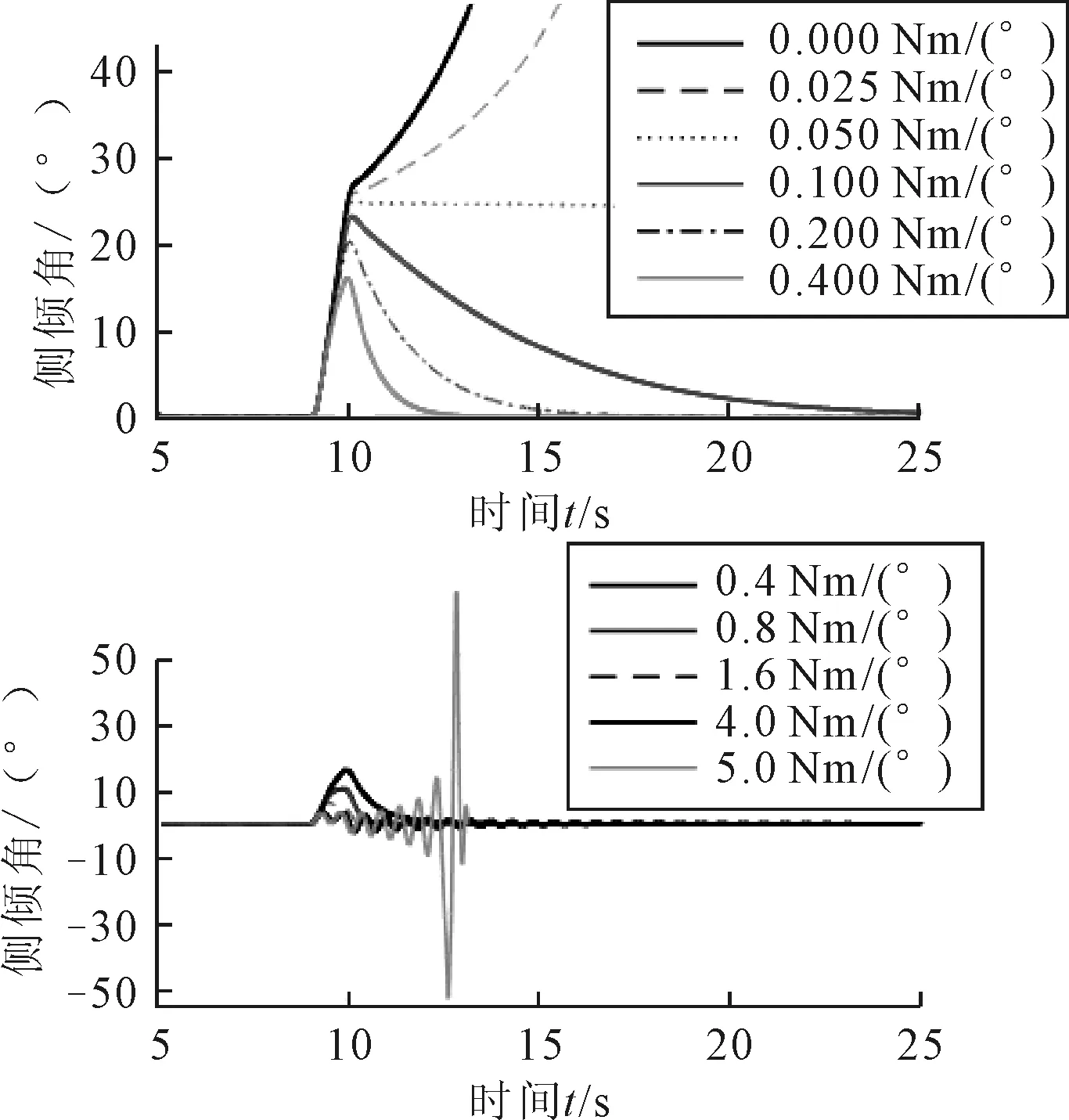
图9 侧倾刚度对干扰下侧倾角影响

由图10可知，当轮胎侧偏刚度大于40 N/(°)时，可使车辆稳定。在满足车辆稳定的条件下，增加侧偏刚度可减小侧倾角扰动。

质心X位置表示从前轮轮心至后总成质心的X向距离。由图11可知，质心X向位置在130～1 350 mm范围内车辆的稳态运动是稳定的。在稳定范围之内适当前移可使扰动侧倾角减小且减小回复时间。

图10 侧偏刚度对干扰下的侧倾角影响

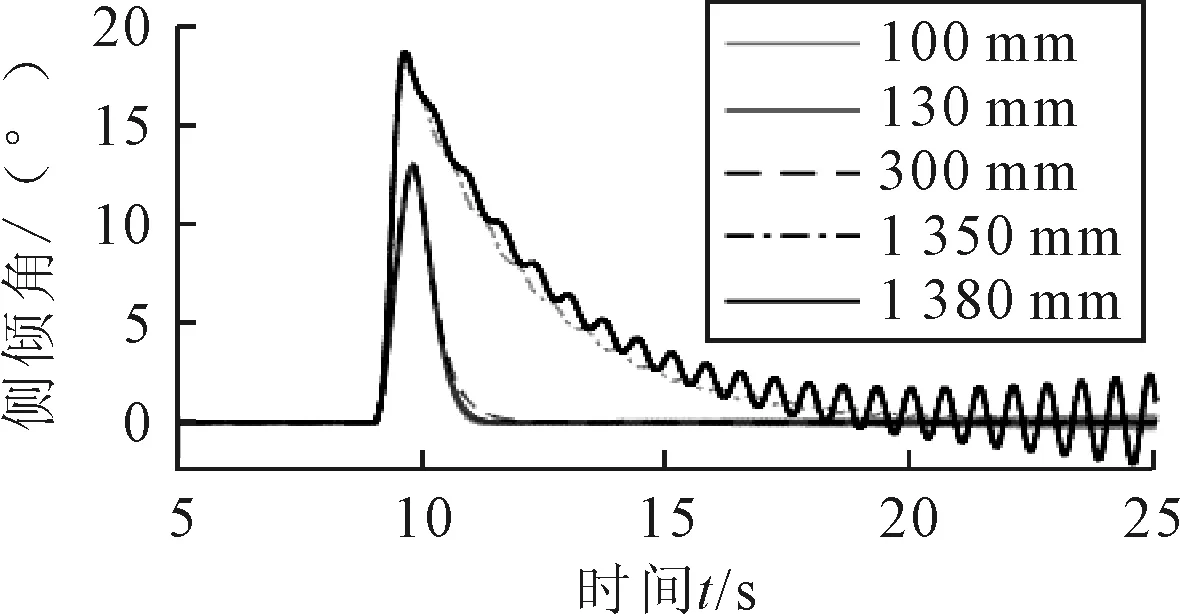
图11 质心X向位置对干扰下的侧倾角影响

4 结论

(1)以齐次坐标描述单轨迹车辆各部件的位置和姿态，考虑轮胎力矩，建立了9自由度非线性模型DOF9-BIKE。在典型工况下，仿真验证了所建模型的正确性。

(2)将模型转化为Воронец方程形式。根据Lyapunov稳定性理论计算了单变量下单轨迹车辆稳态运动稳定性的条件。从计算结果及验证可以看出，车速超过某一限值，足够的轮胎侧偏刚度是保证单轨迹车辆稳态运动稳定性的必要条件。车速增大可使侧倾角扰动幅值减小但回复时间增加，增大侧偏刚度可减小扰动幅值。对于具体的车辆，转向器阻尼、轮胎侧倾刚度、质心位置都应满足一定的取值范围，才能使车辆稳态运动稳定。