微纳晶体谐振器封盖移载机械手末端位置误差分析

周晨珺,胡 剑,喻信东,肖 佩,李刚炎

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北泰晶电子科技股份有限公司，湖北 随州441300)

封盖移载机械手运动学是对于末端执行器与各个关节在空间位置和姿态的关系研究。李保丰[1]、陈支等[2]运用DH(Denvit-Hartenberg)代数法建立相关的DH参数误差模型，但DH参数法在相邻关节轴相互平行或者接近平行的情况下，DH模型存在参数的奇异性和突变性的缺点。

为了解决DH模型在相邻关节轴相互平行或者接近平行时存在的问题，引入MDH(modified denvit-dartenberg)矩阵，分析封盖移载机械手的正运动学[3]。基于Robotics Toolbox工具箱对所建立的运动学模型进行仿真，验证建立的MDH参数[4]。通过所建立的MDH模型引入微分思想，建立封盖移载机械手的误差模型[5-6]，通过Matlab对MDH模型的各个参数引入误差，得到对应误差参量的末端位置误差图，从而为封盖移载机械手的设计和安装提供理论依据。

1 封盖移载机械手运动学模型建立

1.1 封盖移载机械手的结构与功能

所研究的封盖移载机械手主要运用在SMD(surface mounted devices)封装设备当中，是其中的关键部件，如图1所示。该机械有4个自由度， 3个旋转关节和1个移动关节，其中关节1、关节2、关节3的3条轴线相互平行，关节4的轴线与其他3条轴线相互垂直。该封盖移载机械手移载封盖到指定位置并能调整封盖的方向使封盖放入后续工位，其运动区域类似一个扇形区间。该设备结构简单、移载速度快。

图1 某封盖移载机械手三维图及其坐标系的建立

1.2 封盖移载机械手DH数学模型建立

按照DH模型建立方法，依次建立各个关节的坐标系。建立的各关节坐标系及连杆参数如图2所示。根据各连杆之间的关系可得DH参数，如表1所示。其中，ai为各连杆长度；αi为连杆的扭角；θi为各连杆的夹角；di为各连杆的偏置。

图2 某封盖移载机械手结构简图及坐标系的建立

iai/mmαi/(°)θi/(°)di/mm12250θ100～90°2-00d2-20～-10 mm30-90θ3-85180～270°4200θ4067.5～90.0°

1.3 封盖移载机械手MDH数学模型的建立

虽然DH参数法已经广泛应用于封盖移载机械手运动学建模与分析中，但机械手相邻连杆轴线平行，两轴的微小夹角会使两轴的公法线位置产生很大的偏差，从而使建立的模型不准确。为了解决相邻关节平行时DH模型的局限性，一些学者提出5参数的MDH模型。该模型是在原有的a、α、θ、d4个参数基础上引入了一个绕Y轴旋转的转角β。而在坐标系的建立中，对于旋转关节和移动关节有两种不同的建模方法。根据本机构有3条轴线相互平行的特点，可以得到本封盖移载机械手的MDH参数，如表2所示。

表2 封盖移载机械手的MDH参数

1.4 封盖移载机械手的正运动学分析

正运动学方程描述了封盖移载机械手末端执行器的位置和姿态，是进行运动学分析的基本方程。根据文献[7]可得坐标系变换矩阵Ti-1,i为：

(1)

式中：cθi、sθi分别为cosθi、sinθi；cαi、sαi分别为cosαi、sinαi；cβi、sβi分别为cosβi、sinβi。

由此可以得到4个连杆的变换矩阵：

根据已知的各相邻杆的齐次变换矩阵，将各连杆的齐次变换矩阵相乘可得末端执行器的位姿方程(又称正运动学模型)：

T0,i=T0,1(θ1)T1,2(d2)T2,3(θ3)T3,4(θ4)

(2)

根据式(2)可得正运动学方程：

(3)

式中：nx=cθ4c(θ1+θ3);ox=-sθ4c(θ1+θ3);ax=-s(θ1+θ3);px=20cθ4c(θ1+θ3)+225cθ1;ny=cθ4s(θ1+θ3);oy=-sθ4s(θ1+θ3);ay=c(θ1+θ3);py=225sθ1+20cθ4s(θ1+θ3);nz=-sθ4;oz=-cθ4;az=0;pz=d2-20sθ4-25。

基于式(3)求得封盖移载机械手的末端执行器的位置和姿态。已知封盖移载机械手各个关节的位置参数θ1、d2、θ3、θ4的初始位置，当给定各个关节变量时，根据式(3)求得唯一的T0,4与之对应。

1.5 基于Robotic工具箱的封盖移载机械手运动学仿真

封盖移载机械手的运动仿真采用Robotics Toolbox[8]来完成，对于连杆的建模需要调用Link函数。其编程语句如下：

L1 = Link(′d′, 0, ′a′, 225, ′alpha′, 0);

L1.qlim=[0,pi/2];

L2 = Link(′theta′, 0, ′a′,0, ′alpha′,0);

L2.qlim=[-20,-10];

L3 = Link(′d′, -85, ′a′,0, ′alpha′, -pi/2);

L3.qlim=[pi,3*pi/2];

L4 = Link(′d′, 0, ′a′, 20, ′alpha′, 0);

L4.qlim=[3*pi/8,pi/2]

bot = SerialLink([L1 L2 L3 L4], ′name′, ′my robot′)

q1=[0 -10 pi pi/2];

bot.plot(q1,′workspace′,[-250,250,-250,250,-250,250]);

bot.teach()

已知封盖移载机械手的初始位置，各关节位置参数为：θo1=0°、do2=-10、θo3=180°、θo4=90°，取料工位各关节的位置参数为：θk1=0°、dk2=-20、θk3=270°、θk4=67.5°，放料工位各关节位置参数为：θr1=90°、dr2=-20、θr3=270°、θr4=90°。通过plot函数在Matlab中绘制出封盖移载机械手的模型，利用示教模式手动对模型运动轨迹进行仿真，通过已知各个工位各关节位置参数，得到初始位置、取料工位位置和放料工位位置如图3所示，其中箭头表示机械手在这3个工位相互变化。

图3 基于Robotics工具箱的仿真建模

从图3可知，封盖移载机械手在各个工位时各连杆的位姿满足要求，因此本MDH参数在Robotics Toolbox中所建立的模型是有效的。

2 封盖移载机械手的末端位姿误差建模

2.1 封盖移载机械手的误差分析

封盖移载机械手的几何参数误差，主要包括关节的连杆长度误差Δai、连杆的扭角误差Δαi、连杆的转角误差Δθi、连杆的偏置误差Δdi等[9-10]。而这些误差中，连杆的长度误差Δai和连杆的偏置误差Δdi是由于制造加工和安装而产生的；连杆的转角误差Δθi主要来源于编码器的零位误差；连杆的扭角误差Δai主要来源于相邻关节轴线的垂直度或者平行度的偏差。连杆参数误差示意图如图4所示。

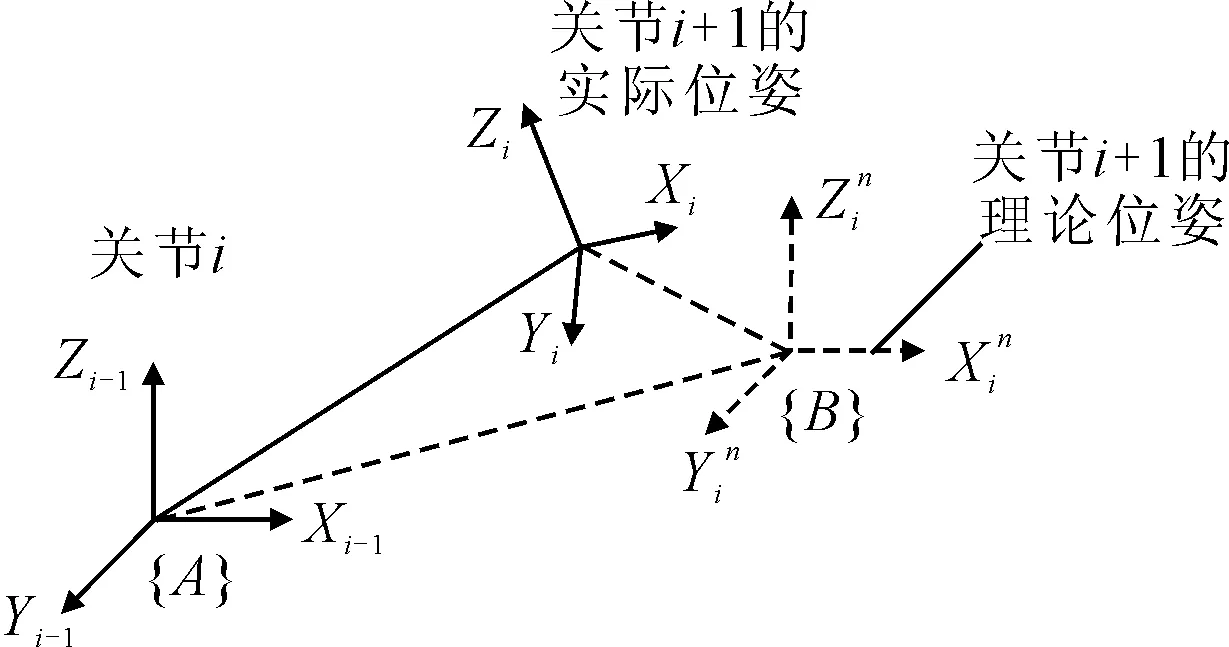
图4 连杆参数误差示意图

2.2 封盖移载机械手的末端位姿误差模型

在理想情况下，封盖移载机械手的末端执行器的位姿始终与设备控制器指令的位姿一致。但在实际情况下，误差是不可避免的，因此封盖移载机械手的末端执行器的位置始终会与理想情况不一致。基于微分思想，可以把各关节产生的误差引入到末端执行器坐标系，然后再根据末端执行器的位置偏差从而建立起封盖移载机械手的几何误差模型。

笔者以封盖移载机械手为研究对象，由于封盖移载机械手第1关节、第2个关节和第3个关节平行。根据上述分析，DH矩阵在相邻轴平行的情况下有一定的局限性，因此采用MDH矩阵建立几何误差模型，对于非相邻平行的轴继续采用DH方法建模。

根据MDH模型封盖移载机械手连杆的变换矩阵可以表示为：

Ti-1,i=Rot(Zi-1,θi)Trans(Zi-1,di)×

(4)

由于受到几何误差的影响，在实际情况下的齐次变换矩阵为：

RTi-1,i=Rot(Zi-1,θi+Δθi)×

(5)

因此可得连杆i的误差模型为：

d(Ti-1,i)=RTi-1,i-Ti-1,i=Ti-1,iΔi

(6)

式中：Δi为微分变换矩阵，根据微分运动学可以表示为：

(7)

式中：δx、δy、δz分别为x、y、z方向的旋转距离。

由于Δai、Δαi、Δdi、Δθi和Δβi在实际情况下都比较微小，因此在这种情况下可用连杆的微分模型来替换，此时全微分连杆的微分模型为：

(8)

由式(6)可求得Δi，见式(9)；由此，根据式(7)和式(9)可得式(10)。

(9)

(10)

将式(10)以微分运动向量的形式ΔLi=[Δai,Δαi,Δdi,Δθi,Δβi]对其进行表示：

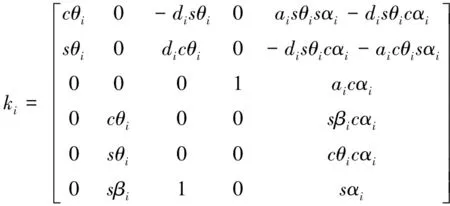
(11)

式中:Gi为误差系数矩阵，关节误差ki只是相对于工具坐标系而言，因此需要将这些误差变换到基坐标下，其变换公式如下：

(12)

式中，Bi,4为i关节的坐标系位姿误差转换到末端执行器的坐标系位姿误差的转换矩阵。

Diei

(13)

根据式(13)，可得封盖移载机械手的末端位姿误差公式：

(14)

式中:J为扩展雅克比矩阵，ΔL=[Δa1,…Δa4，Δα1,…,Δα4，Δd1,…,Δd4，Δθ1,…,Δθ4,β1,β2]为有待辨识的参数误差值，根据封盖移载机械手的机械结构中1、2、3轴都相互平行的特点，因此在2轴和3轴上引入旋转参数β1、β2，因此在ΔL中包含了β1、β2两个旋转参数。

3 封盖移载机械手的末端位置误差仿真

3.1 基于Matlab的末端位置误差仿真

位姿误差模型分为末端执行器的位置误差模型和末端执行器的姿态误差模型。在通常情况下，末端执行器的姿态是很难测量出来的。因此笔者仅基于位置误差模型，把MDH模型中5个参数的误差用末端执行器中心位置坐标表示。根据位置误差模型利用Matlab软件编程的方式来进行实例计算。Matlab的编程流程如图5所示。

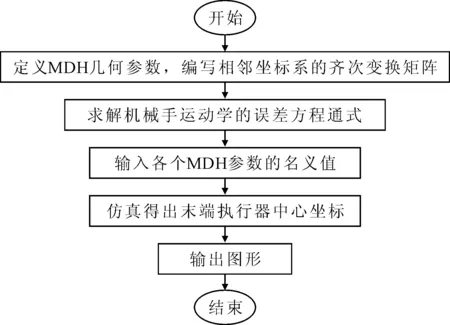
图5 Matlab编程流程

分别给Δαi、Δθi、Δβi赋5个值，分别取0.01～0.05 rad，给Δai、Δdi赋值为0.1～0.5 mm，由于关节1、关节2、关节3相互平行，根据MDH的建模原则，关节1中的Δd1、关节2中的Δα2和Δθ2始终为0，由此可得相对应坐标点的末端位置误差，结果如图6～图9所示。

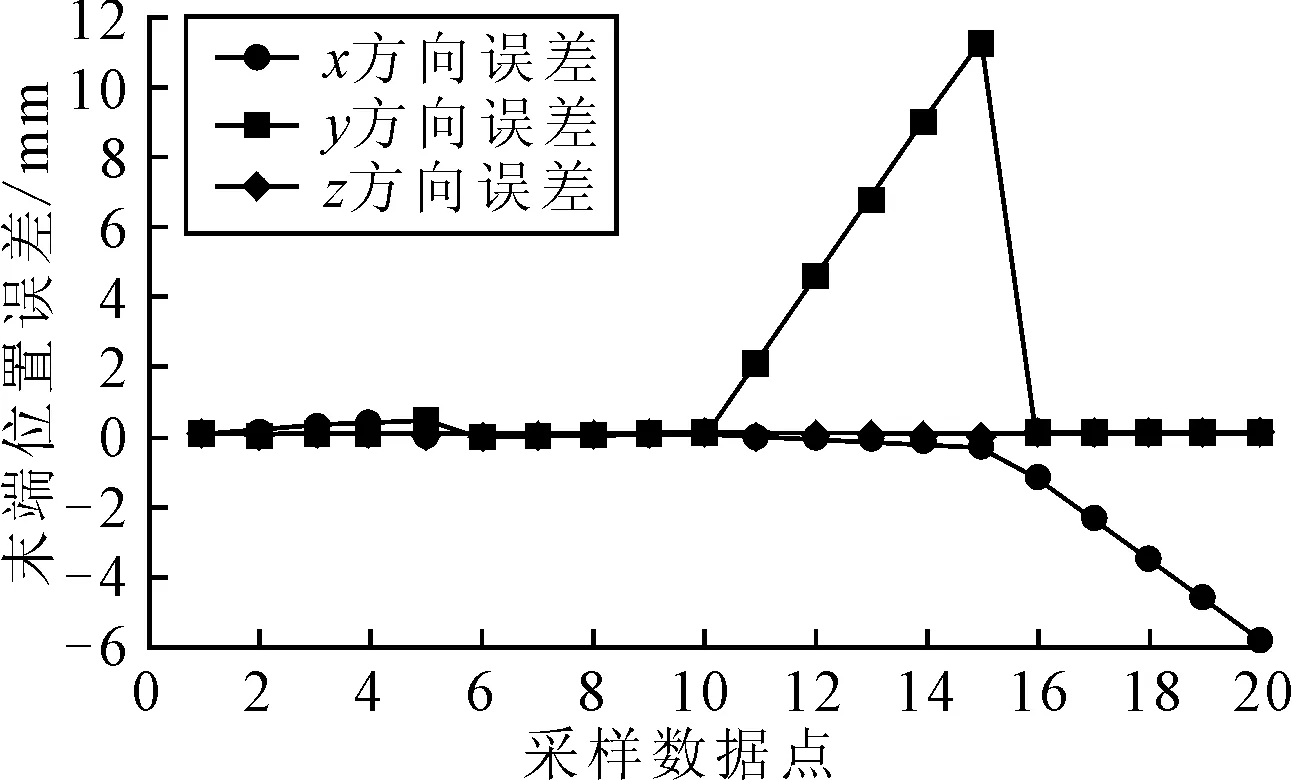
图6 关节1上各参数误差对末端X、Y、Z方向位置误差

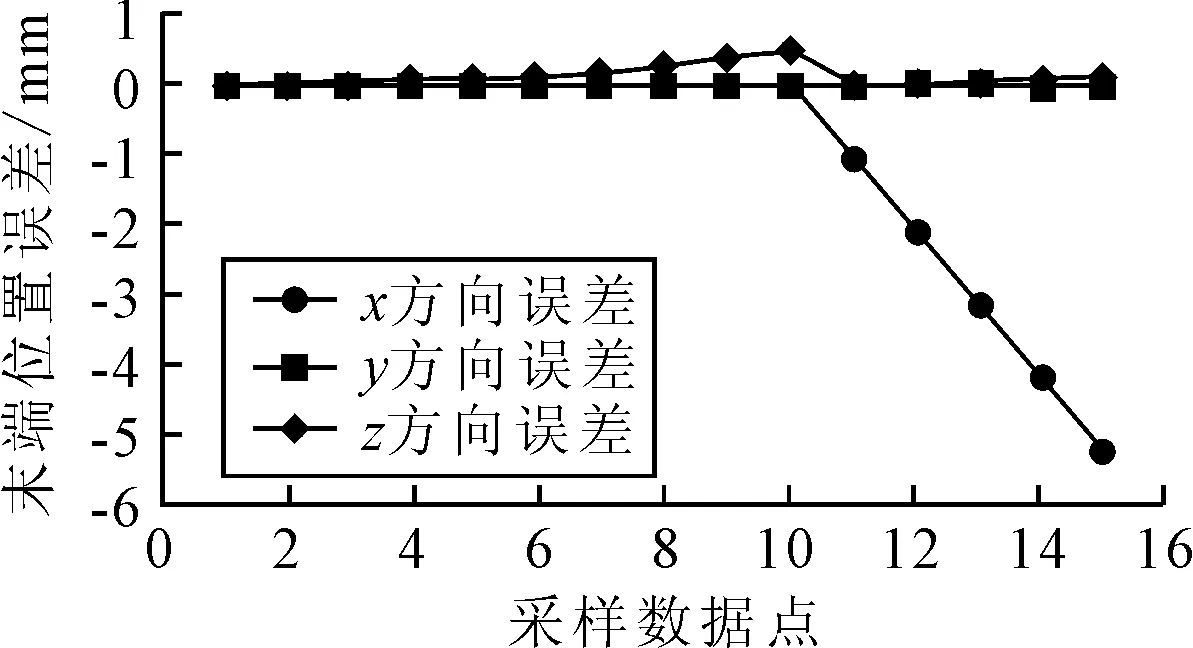
图7 关节2上各参数误差对末端X、Y、Z方向位置误差

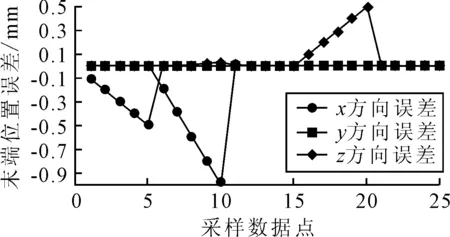
图8 关节3上各参数误差对末端X、Y、Z方向位置误差

图9 关节4上各参数误差对末端X、Y、Z方向位置误差

3.2 仿真结果分析

由图6～图9可知，4个关节中在不同误差参数影响下的效果是不一样的。

对于关节1而言，Δa1和Δα1的误差对末端位姿影响极其微小，因此对于两轴线之间的距离和关节1和关节2之间公法线的夹角处误差可以适当放宽。Δθ1误差对于末端位姿的Y方向位置误差有很大的影响，Δβ1对于末端位置X方向位置误差有很大的影响，因此关节1的原点定位要保证高度精准，同时在设计和安装的过程中尽量保证关节轴线转角，其他两个关节平行。

对于关节2而言，Δα2随着误差增大对末端位置的Z方向有较小的影响，因此在设计和安装中可稍微放宽对相邻轴线公法线的夹角要求。而Δd2对末端位置的Z方向位置误差有一定的影响，这时对关节2的原点定位提出了较高的要求，在安装中一定要保证移动关节的原点位置精度，并同关节1一致。由于Δβ2的误差值对末端位置的X方向影响很大，因此要保证关节1、关节2、关节3的轴线尽量平行。

对于关节3而言，Δa3、Δα3、Δd3分别对末端位置的X、Y、Z方向有很大的影响，因此要保证关节3旋转轴的下端夹取位置的安装精度，同时也要保证零件的公差标注合理，与关节4安装的垂直度满足精度要求。Δθ3和Δβ3误差对末端位置影响不大，因此对轴3和轴4之间轴线的夹角值和两轴是否绝对垂直可适当放宽要求。

对于关节4而言，主要影响末端位置精度的误差量为Δa4和Δθ4，因此一定要保证影响零件末端位置到关节轴线的精度，加工误差在可控范围，而且对于关节4转动的原点精度必须要满足精度要求。Δα4和Δd4则对末端位置的影响不大，在设计和安装时可以适当放宽要求。

4 结论

在使用传统DH模型的基础上，针对关节轴线平行时DH模型有一定局限性的缺点，采用MDH模型建立某型封盖移载机械手的运动学模型。同时通过MDH模型推导了封盖移载机械手的正运动学模型。利用Robotics Toolbox对封盖移载机械手进行仿真，验证所建立MDH模型的合理性。根据MDH模型建立了某型封盖移载机械手的误差模型，利用Matlab软件编程的方式对误差模型中5个误差参数进行计算，分析了各个关节中影响大的误差参数并提出了解决方法，为封盖移载机械手的位置精度设计和安装提供理论依据。