基于冲击试验的座椅骨架结构优化设计

叶 畅，周廷美，莫易敏，吕俊成，高 烁，刘青春

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 545007)

汽车座椅主要是由座椅骨架、调节机构、蒙皮、发泡填充物以及塑料附属部件组成，其主要的受力部件是座椅骨架及调节机构，在车辆受碰撞冲击中，直接影响着座椅的强度。而后排座椅在碰撞事故中还可能受到座椅后方行李箱的惯性冲击，产生的冲击力会对乘员造成额外伤害，因此对后排座椅抗冲击性能的研究十分必要[1]。

针对汽车座椅安全性的优化设计研究，大致可分为静态结构优化与动态结构优化，静态结构优化多用拓扑优化等方法来实现，而动态结构优化多用参数优化理论结合动态试验来实现。白煜等[2]采用轻量化材料和结构拓扑优化方法，提出一种碳纤维复合材料座椅设计方法；Jeya等[3]比较研究了速度设定为40.2 km/h的后部台车试验中传统座椅和含安全带约束座椅上假人的生物力学响应，将座椅靠背刚度作为后部碰撞中乘员伤害风险指标进行分析；Keysun等[4]通过对汽车座椅骨架结构进行强度分析，确定座椅骨架关键受力部位，并对其刚度进行优化设计；陈道炯等[5]通过分析座椅靠背单一参数在靠背的不同测点下的曲线变化，在上框钢管厚度和直径的变化敏感度不大时，采用最大应力较小的组合进行优化；葛如海等[6]采用灵敏度分析的方法探寻座椅安全性最显著的影响因素，用正交试验的理论，对这几项因素进行综合优化。

国内外的相关研究多以提升座椅刚度为优化目标，较少从座椅动态特性的研究着手，且相关优化方法多采用枚举比较的方式，缺乏科学的参数优化模型。笔者利用参数优化相关理论，以提升后排座椅的动态特性为基础，建立某汽车后排座椅及连接车身部分结构的有限元模型，与相关法规的试验工况一致来进行模型处理，实现行李箱冲击动态仿真，通过分析座椅的受力情况找出关键部件，利用最优拉丁超立方设计方法，建立Kriging模型，通过NSGA-Ⅱ遗传算法进行多目标优化。

1 行李箱冲击试验及相关法规要求

1.1 行李箱冲击动态试验

在突然制动或发生碰撞下，为保护后座乘员免受因行李惯性冲击造成的伤害，需对汽车座椅进行行李箱冲击试验。所研究的某汽车座椅实际为中排两独立座椅，该车型为7座，当放置行李时，需将最后一排座椅折叠，将行李放在其平面上，按照法规GB15083-2006[7]要求，该车型需对倒数第二排即中排座椅进行试验。

法规试验要求将两个边长为300 mm，边棱倒圆角半径为20 mm且质量为18 kg的立方体试验块并排放置于行李舱的地板上，两试验块的内侧边缘距离车辆纵向中心面25 mm，位于座椅靠背后方，纵向上距离座椅靠背200 mm，并将头枕至于可调最高位置，试验块的摆放位置如图1所示。

图1 试验块摆放位置示意图

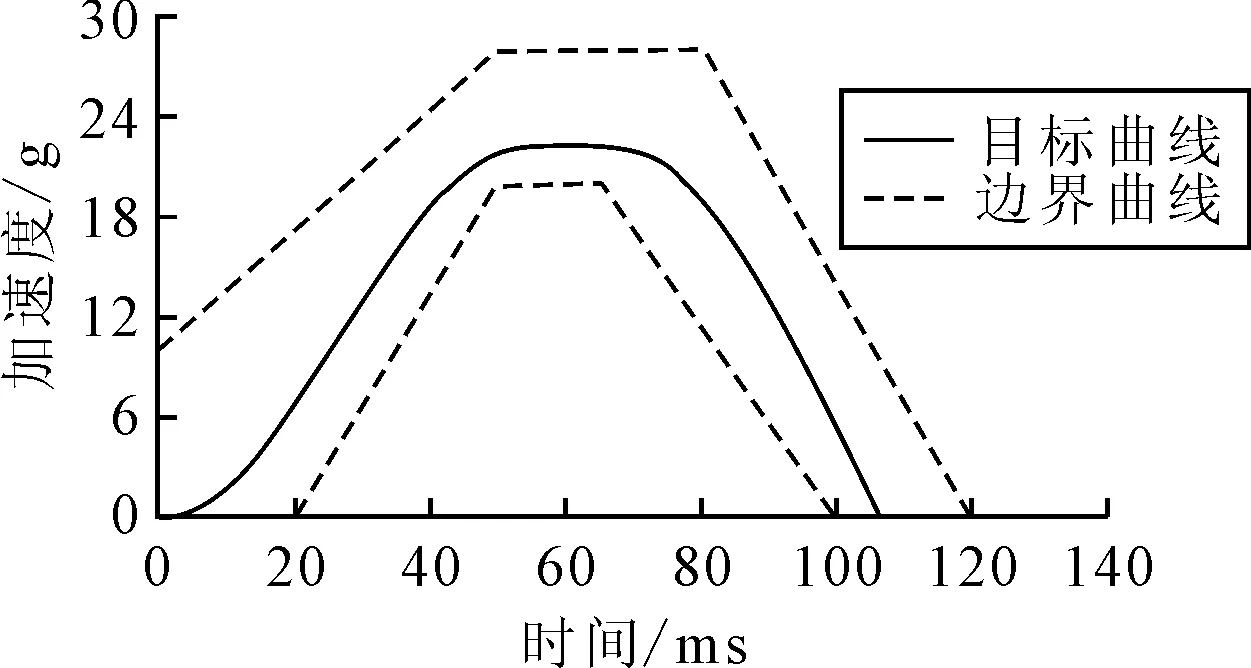
图2 加速度曲线

1.2 相关法规要求

为防止移动行李对乘员伤害，法规规定如下：

对于座椅位移折叠装置、调节装置和锁止装置，允许发生永久变形但不允许失效，并保持在原位置，且座椅不产生会对乘员造成伤害的尖棱或凸起。

试验期间，座椅头枕部分前轮廓不能向前方移出经过座椅R点前150 mm的一横向测试平面，定义头枕移动最大位置与测试平面的距离为位移余量，值为正表示未超过测试平面，值为负表示超过测试平面，位移余量越大说明座椅抗冲击性能越好，按法规要求位移余量需大于0，试验要求如图3所示。

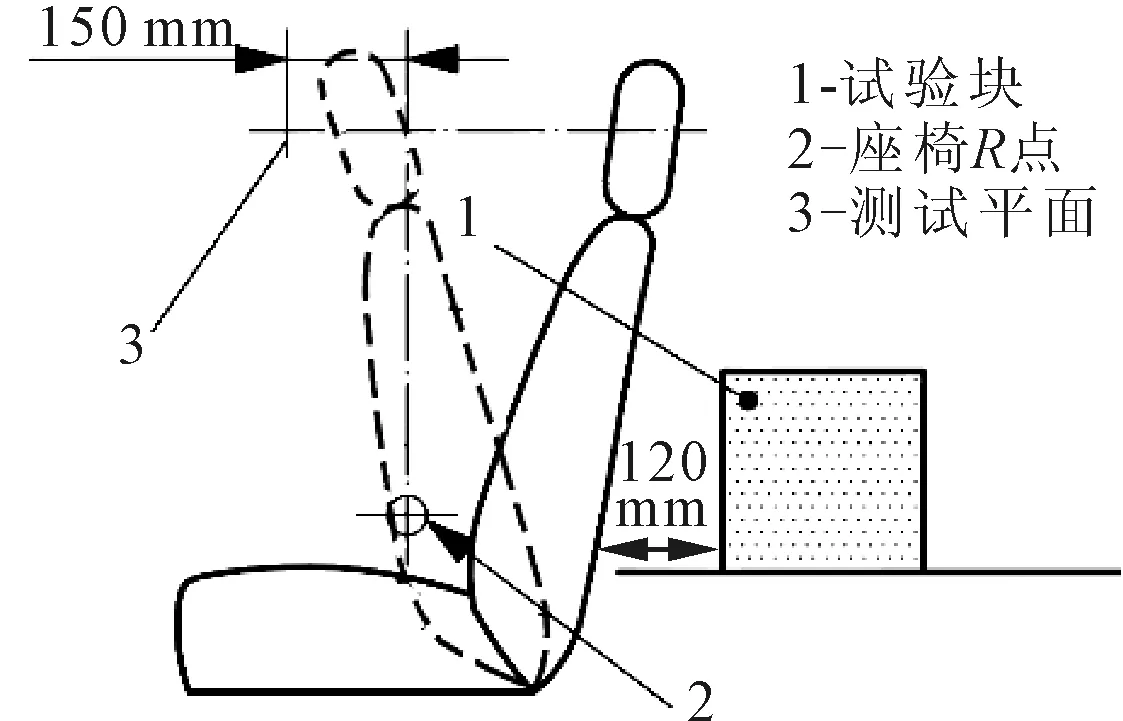
图3 法规试验要求示意图

2 有限元模型建立与分析

2.1 汽车座椅行李箱冲击模型

2.1.1 模型简化

所研究车型结构复杂，为节约时间成本，整体上在原试验车模型上进行简化，保留中排座椅及其车身连接部件，去除非研究对象的其他座椅、影响不大的上车身和其他部件，用一个水平面替代后排座椅折叠后形成的平面。

座椅模型只对座椅骨架等金属部件建模，由于发泡填充物对座椅强度几乎没有影响，省去对发泡填充物等非金属部件的建模，既能减少运算单元数，又可以在一定程度上避免泡沫材料在计算中产生负体积而导致计算终止的现象。为进一步减少模型计算时间，考虑到模型加速度曲线的时间历程，整个运动过程只考虑前150 ms的状态。整个模型多采用壳单元，对简化后的模型用HyperMesh进行网格划分，仿真模型如图4所示。该模型共有700 217个单元，738 194个节点。

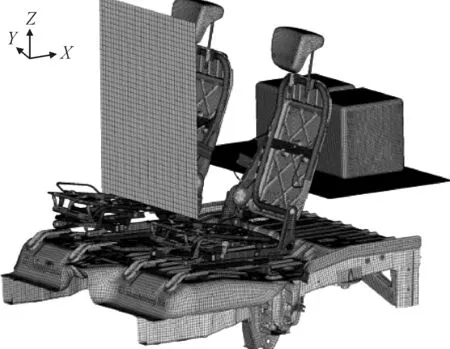
图4 仿真模型

2.1.2 接触与连接的设置

定义接触防止相邻表面节点发生穿透，在行李箱冲击试验的有限元模型中，接触的定义有3种：整体各部件自接触、面面接触以及焊点接触。

定义连接对座椅模型中的连接关系进行模拟，采用刚性单元模拟二氧化碳保护焊和螺栓连接，Beam单元模拟点焊连接。座椅的靠背骨架与坐垫骨架由内侧两调角器和外侧两活动销轴连接，其连接关系均用Beam单元与刚性单元联合模拟。

2.1.3 约束与加载条件设置

由于试验台车与下车身焊接，台车带动座椅整体沿水平方向前后运动，为此，约束下车身的自由度，使其只能在X轴方向移动。对整体沿X轴负方向的加载50 km/h的初速度，并对除了两试验块外其他部件施加如图2所示的X轴正方向加速度，最后对整体施加重力加速度。

2.2 仿真结果分析

将模型在Ls-Dyna中进行计算，在HyperView中查看仿真结果。得到如图5所示的行李箱冲击头枕位移图，整个模型处于一个减速状态，当试验块还未撞到座椅时，座椅靠背因自身惯性，在较大的制动加速度下，产生向前的轻微变形，曲线缓慢下降，当试验块撞到靠背后，试验块巨大的惯性冲力使座椅靠背产生较大变形，曲线迅速下降，并随后回弹，曲线迅速上升。曲线波谷所在的时间节点对应座椅靠背变形最大的时刻，即头枕最大位移时刻，从图5可知，座椅受行李箱冲击过程中头枕位移最大时刻为115 ms时，测得位移余量为4.904 mm，虽符合法规大于0的要求，但余量很小，实测中产生的微小误差都有可能使余量降为负值，使得试验结果不满足法规要求。

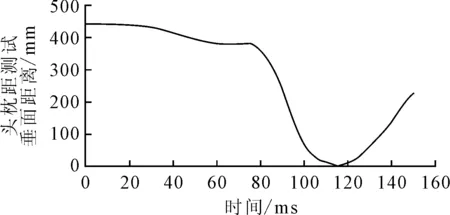
图5 行李箱冲击头枕位移图

从撞击过程中分析得，冲击载荷由靠背骨架传到调节装置，再由调节装置传到坐垫骨架梁结构，选取座椅骨架进行应力云图分析，得到在载荷力传递路径上的关键部件的最大应力值，如表1所示。

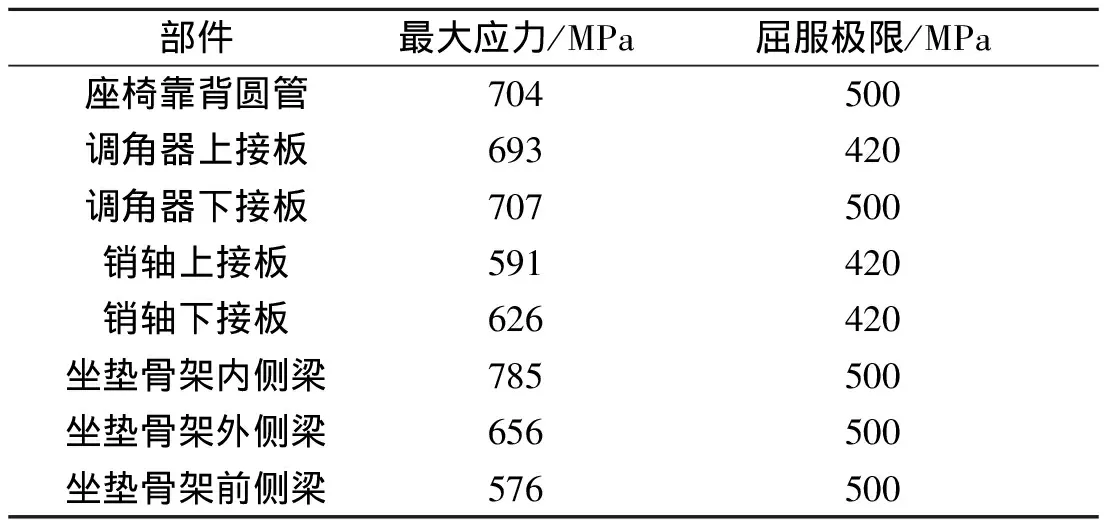
表1 关键部件应力表

从表1可知，载荷力传递路径上的关键部件受到的最大应力均超过各部件材料的屈服极限，产生塑性变形，其中坐垫骨架内测梁与调角器下接板连接处应力集中较严重，最大应力为785 MPa，有一定的撕裂风险，从而产生对乘员造成伤害的尖锐物。

3 座椅骨架优化

3.1 优化模型建立

通过表1选取出座椅骨架中应力较大的5个部件，即座椅靠背圆管、调角器上接板，调角器下接板、坐垫骨架内侧梁以及坐垫骨架外侧梁，以其厚度分别为t1、t2、t3、t4、t5作为优化设计变量，以最大头枕位移余量和最小总质量为优化目标，以被优化部件的最大应力小于785 MPa和位移余量大于0为约束条件进行优化。

针对上述设计方案，建立其数学模型：

(1)

3.2 优化方法

3.2.1 最优拉丁超立方抽样

最优拉丁超立方抽样(optimal latin hypercube sampling, Opt LHS)在拉丁超立方抽样的基础上进行改进，保留抽样的不可重复性，又使样本点尽量均匀地分布在样本空间里。在初始参数的基础上建立如表2所示的样本空间[8]。得到30组样本点，如表3所示。并分别对其进行仿真建模并计算，获取其样本信息及仿真结果。

表2 抽样样本空间 mm

3.2.2 Kriging近似建模

Kriging又称空间局部插值法，是以变异函数理论和结构分析为基础，在有限区域内对区域化变量进行无偏最优估计的一种方法，具有很好的适用性。以t1、t2、t3、t4、t5为输入，L、mass和σmax为输出，对这30个样本数据建立Kriging模型[9]。

为保证近似模型的可信度，通常选择可决系数R2和平均误差μx来衡量模型的拟合程度，R2值越接近1，μx值越接近0，说明拟合程度越好，通过比较输出的R2值和μx值，选取可信度最高的模型，最终采用的拟合类型为各向异性，拟合函数为指数函数类型的Kriging模型，其拟合精度如表4所示。

表3 30组样本点数据

表4 拟合精度

从表4可知，该模型的拟合精度较高，具有较好的可信度。

3.2.3 NSGA-Ⅱ多目标优化

NSGA-Ⅱ是目前运用最为广泛的多目标优化算法之一，通过NSGA-Ⅱ算法得到的Pareto前沿，在这一系列非劣解集中选择最合适的方案得到最终优化结果[10]。

运用NSGA-Ⅱ在Kriging近似模型的基础上进行优化，按已建好的数学模型设定其上下边界、约束条件和优化目标，得到一组均满足条件的解，由这组解形成如图6所示的Pareto前沿图。

图6 Pareto前沿

图6中所有的点都是符合条件的非劣解，都满足总质量小于初始总质量7.642 kg，且位移余量均大于0，满足法规要求。从图6可以看出，所选部件的总质量越高，位移余量就越高，座椅抗冲击的动态性能越好，轻量化与高抗冲击性能具有矛盾的关系，符合实际情况。

为确定最终优化方案，需从中选择合适的解，由NSGA-Ⅱ算法的寻优策略，具有越大拥挤距离的个体其优越性越高[11]，经算法权衡后，得到如表5所示的参数优化值。

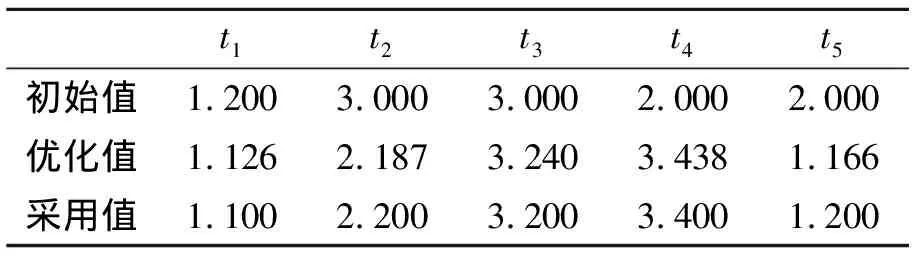
表5 参数优化值 mm

3.3 优化结果验证及分析

将实际采用的优化方案代入到行李箱冲击有限元模型中进行计算，得到其优化后的位移余量，优化前后的位移余量如图7所示。

从图7可知，曲线在前段时间基本重合，在后段时间有所改变，说明优化对撞击前状态影响不大，对撞击后的过程影响较大。优化后的曲线波谷相较于优化前的曲线波谷有所上移，即靠背受冲击弯折的程度减弱，位移余量L提高，座椅动态性能提升。

优化结果如表6所示，从表6可知，优化结果的预测值与实际值的误差很小，验证了优化结果的可靠性。在均衡了各部件厚度的分配之后，使优化前存在的位移余量L不足的状况得到明显改善，安全裕度显著提高，并且在部件最大应力σmax降低8.32%的同时，总质量降低了4.44%。

4 结论

笔者基于汽车后排座椅行李箱冲击试验的有限元模型，采用参数优化理论对座椅骨架关键结构的厚度进行重新分配，得到提升座椅动态特性的优化方案。优化过程利用最优拉丁超立方设计的方法，得到样本点数据，并建立Kriging近似模型，将实际工程问题转化为数学模型，通过NSGA-Ⅱ遗传算法对该模型进行多目标优化，优化后的结构参数提升了座椅动态特性，降低座椅骨架最大应力，并兼顾了轻量化的目标，对提升座椅动态特性的结构设计提供了参考。

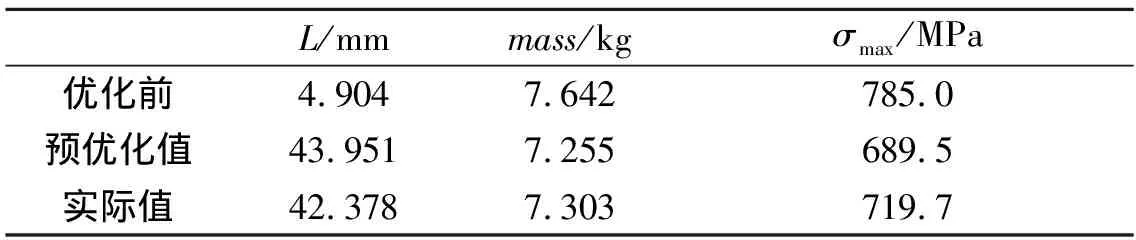
表6 优化结果对比