特征结构配置法在无人机控制系统中的应用
盛启辉,万 茜,王小梅,刘 倩,李 宇
(航空工业洪都,江西 南昌,330024)
0 引言
线性系统的时域性能指标要求可转化为期望极点,再根据期望极点的位置,利用状态反馈、输出反馈对系统进行极点配置。但是,对于一个确定的状态反馈极点配置问题,当采用不同的方法去求解时,可以得到不同的状态增益,即其解不存在惟一性。特征结构配置不但配置闭环系统的极点,而且还配置它们的重数并同时配置闭环特征向量,因而可以更加准确地掌握系统的性能。特征结构配置的另一个优点在于,通过适当选取设计参数,可以实现期望性能的控制系统[1-2]。本文运用输出反馈特征结构配置设计了无人机飞行控制系统的控制律,对极点和特征向量进行了期望的配置,实现了系统模态的解耦。
1 输出反馈特征结构配置
1.1 特征结构配置分析
线性系统的状态方程可表示为
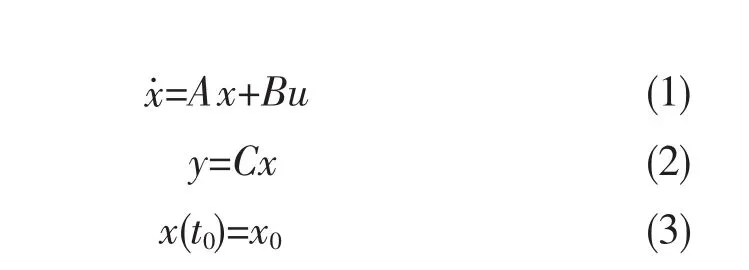
其中A为系统的状态阵,反映系统固有运动特性;B为控制阵,反映输入量对系统运动状态的影响;C为输出阵,确定了系统的输出状态量。x为系统运动的状态向量,u为系统的输入向量,y为系统的输出向量,x0为初始值,t0为初始时间。
则系统的解为x(t)=eAtx0。
若用A的特征向量和特征值表示,特征系统方程为

其中特征向量V与特征值λ分别为:

特征向量V是状态空间的基本集,状态空间的任一向量可表示为系统特征向量的线性组合,这些特征向量称为系统的右特征向量。同样,系统还存在左特征向量W,并满足

式中,WT=[W1…W2…Wn] 。
系统时域响应方程为
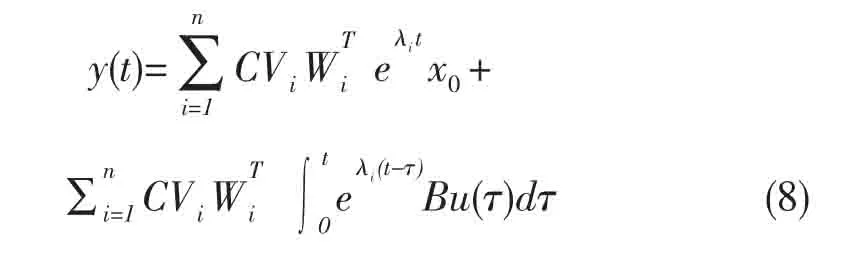
系统自由响应的每个解与三个量有关:确定响应衰减速率或增长率的特征值、确定响应形状的特征向量和确定加入自由响应的每个初始状态;强迫响应与确定的外作用输入有关。不同的特征值及相应的特征向量和外作用输入直接影响系统的过渡过程,系统的时域响应反映了系统运动模态和外作用对输出的影响。
时域响应中的自由响应部分可写成

式(8)和式(9)表明系统的响应可由其特征值和特征向量进行描述,因此如能改变系统的特征结构,将能改善系统的时域响应。
1.2 输出反馈特征结构配置
选取系统所期望的一组闭环特征值λ,进行输出反馈极点配置的控制律形式为[3-4]

K为反馈增益矩阵。
则系统闭环方程

对于特征值λi和特征向量Vi,有

假设系统的期望特征值λ与状态矩阵A的特征值不等,因此(λiI-A)的逆存在。
设向量 zi=KCVi,Ni=(λiI-A)-1B,
那么Vi=Nizi。
特征向量Vi必须位于Ni的列张成的子空间中,一旦期望的特征值已确定,Ni的分布空间便限定了闭环特征向量的选取。而期望的特征向量不属于预先规定的子空间而不能到达,此时需用最可能到达的特征向量来代替理想特征向量该可达向量是在Ni的列张成的子空间上的投影,使所求的特征向量尽可能靠近期望的特征向量。

式中,Vij是指定元素,×是未指定元素即无约束元素。
定义重新排序算子{·}Ri

式中,li是由中指定元素组成的向量,di是由中未指定元素组成的向量。
将向量Ni中的诸行重新排列,并与中重排序的元素一一对应,Ni形式如下
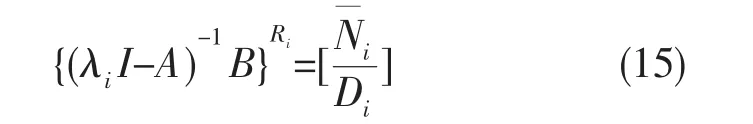
因反馈增益阵满足KCVa=Z,Va和Z的列数与输出变量个数相同,求解式(16)可得反馈增益矩阵K。

2 无人机纵向运动控制律设计
无人机纵向运动方程:

无人机的纵向运动模态可分为两个纵向短周期、一个纵向长周期,期望每个模态起主导作用的分别是攻角、俯仰角速率和俯仰角,期望特征向量为:

运用输出反馈特征结构配置方法得到的无人机俯仰姿态保持系统的反馈增益矩阵:

无人机纵向运动的仿真模型如图1所示。
俯仰角输入指令为0.1754rad(10°),无人机俯仰角响应曲线如图2所示。系统能快速跟踪俯仰角输入指令信号,俯仰角响应无超调,稳态无误差,系统上升时间不大于1.0s,调节时间不大于2.0s。
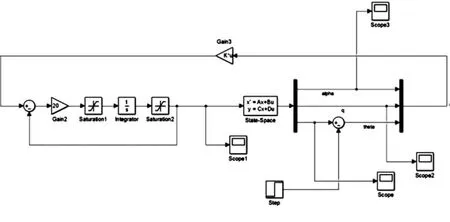
图1 无人机纵向运动仿真模型

图2 无人机俯仰角曲线
图3是无人机俯仰角速率曲线,俯仰角速率在0.6s达到最大,约为 0.27rad/s,1.5s接近 0.0rad/s。

图3 无人机俯仰角速率曲线
图4和图5分别是无人机攻角和升降舵偏转角曲线,攻角1.0s内的增量约0.13rad/s,升降舵偏转角的最大增量约0.44rad/s。

图4 无人机攻角曲线

图5 无人机升降舵偏转角曲线
3 无人机横侧向运动控制律设计
无人机横侧向运动方程:个滚转和一个螺旋,期望每个模态起主导作用的分别是侧滑角、滚转角速率、滚转角、偏航角速率,期望特征向量为:

运用输出反馈特征结构配置方法得到的无人机俯横侧向姿态运动系统的反馈增益矩阵:

无人机的横侧向运动模态可分为两个荷兰滚、一

无人机的横侧向进行协调转弯运动的仿真模型如图6所示。
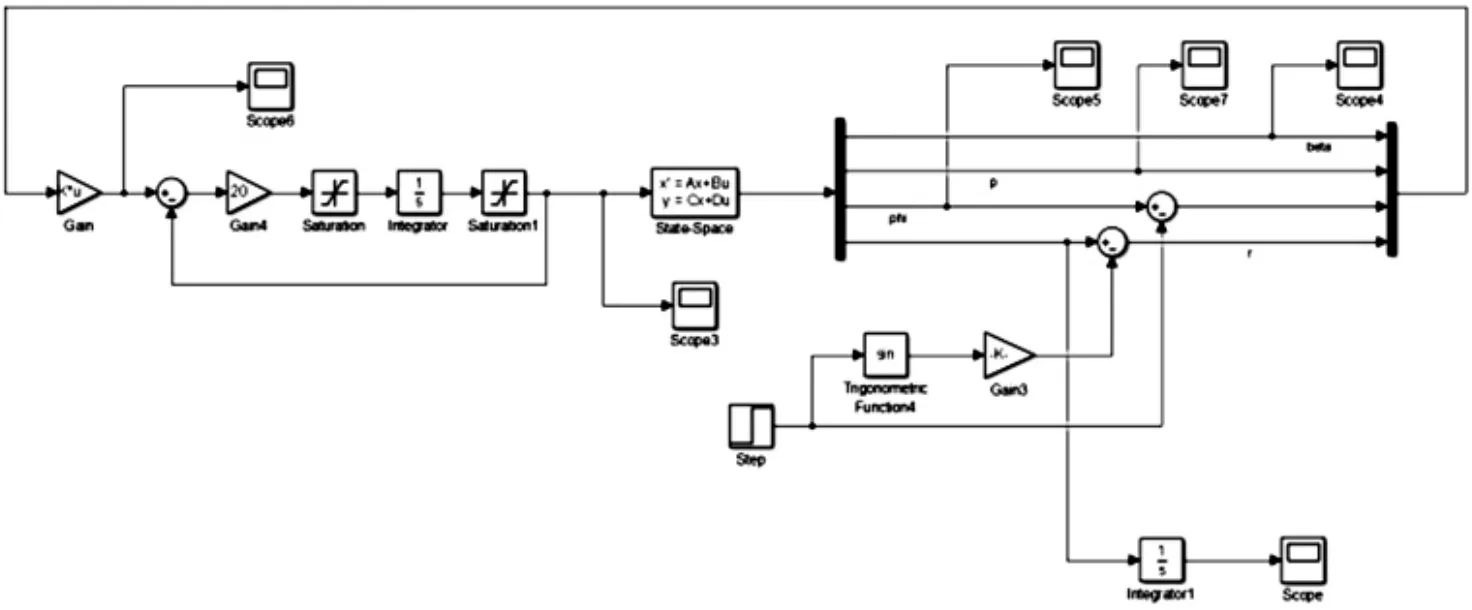
图6 无人机横侧向运动仿真模型
滚转角输入指令为0.52356rad(30°),无人机滚转角响应曲线如图7所示。系统能快速跟踪滚转角输入指令信号,滚转角响应无超调,稳态无误差,系统上升时间不大于1.5s,调节时间不大于2.0s。图8是滚转角速率曲线,滚转角速率0.5s内的增量约0.51rad/s,5s后接近0.0rad/s。
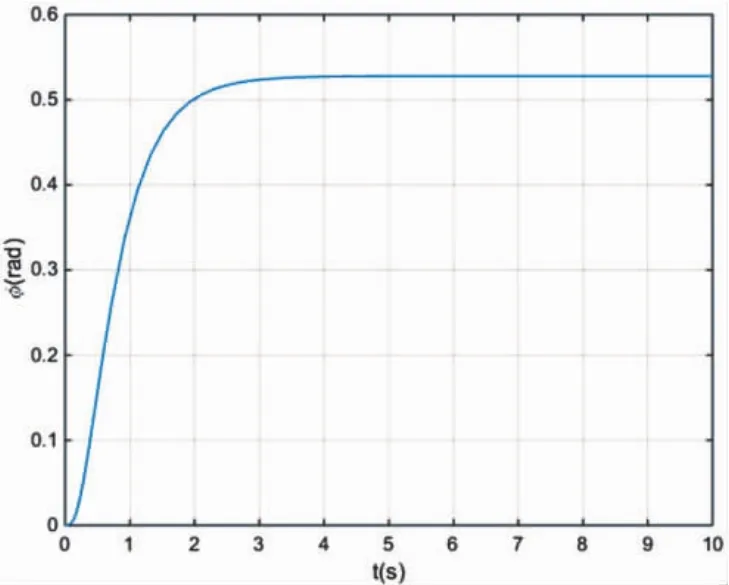
图7 无人机滚转角曲线
图9、图10分别是无人机偏航角速率和偏航角曲线,无人机协调转弯过程中,偏航角速率随着滚转角变化,跟踪滚转指令信号过程中,偏航角速率的增量达到0.06rad/s,滚转角达到稳态,偏航角速率约为0.022rad/s,偏航角随着无人机转弯,10s内变化了0.25rad/s。

图8 无人机滚转角速率曲线
图11是无人机侧滑角曲线,滚转角跟踪指令信号过程中,侧滑角变化0.0085rad,滚转角达到稳态,侧滑角约-0.003rad,协调转弯过程中侧滑角实现了零保持。
图12、图13分别是无人机副翼和方向舵偏转角曲线。副翼偏转角最大增量约0.16rad,稳态值约0.0025rad。方向舵偏转角最大增量约0.11rad,稳态值约0.008rad。
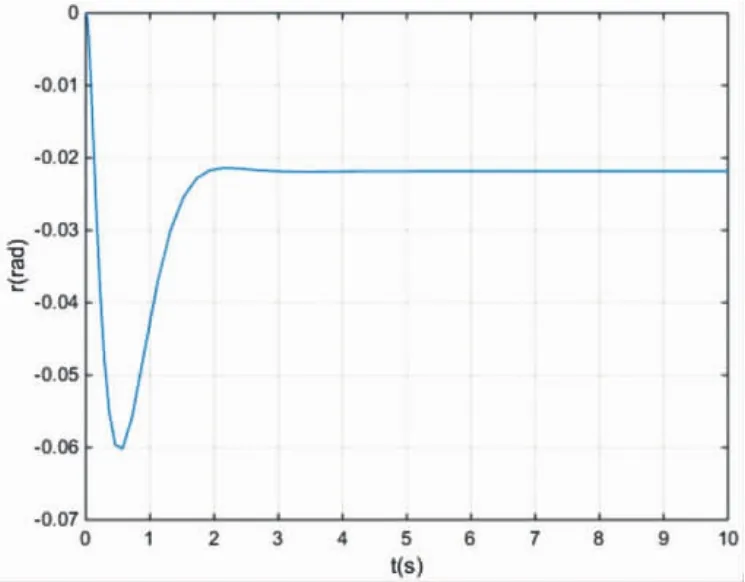
图9 无人机偏航角速率曲线

图10 无人机偏航角曲线

图11 无人机侧滑角曲线
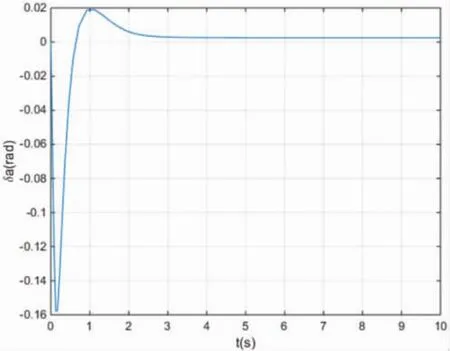
图12 无人机副翼偏转角曲线

图13 无人机方向舵偏转角曲线
4 结论
通过输出反馈特征结构配置设计了无人机的控制律,实现系统内部的解耦,消除不同姿态参数之间耦合作用,实现了不同运动模态最重要状态变量的主导作用。仿真结果表明,俯仰角能快速跟踪指令信号,横侧向运动的协调转弯控制实现了滚转角快速跟踪指令信号、无人机快速转弯以及零侧滑保持,具有较好的飞行动态性能。

