冲击载荷下磁流变阻尼器单神经元PSD算法研究

黄 继，高 佳，段承君，张 浩，韩晓明

(1.山西大学 自动化系，山西 太原 030002；2.山西大学 电力工程系，山西 太原 030002；3.西北机电工程研究所，陕西 咸阳 712099；4.中北大学 机电工程学院，山西 太原 030051)

磁流变阻尼器在结构上比传统的液压阻尼器简单,体积小，方便安装，并且相对于弹簧或液压阻尼器结构一旦确定则阻尼力不可调的缺点，磁流变阻尼器能够输出可实时调节、变换范围宽的阻尼力，且动态响应迅速，可在毫秒级的时间内完成缓冲动作。这完全符合自动武器系统后坐力阻尼器半主动控制的要求，具有很大的优势，因此在自动武器系统后坐力阻尼器半主动控制领域有着良好的应用前景[1-4]。

近年来，大量学者针对磁流变阻尼器的半主动控制提出了多种控制策略，包括滑膜控制、优化控制、神经网络PID控制、自适应控制以及线性二次高斯(LQG)同位控制策略等，均取得了令人满意的控制效果[5-8]。但这些算法的实现均非常复杂，不便于计算机编程实现，对自动武器后坐缓冲控制来说，实时性上均无法保证。对此笔者提出了基于单神经元自适应PSD控制方法，这种算法结构简单，通过编程很容易在计算机上实现，并且对被控对象参数、时滞变化不敏感，可有效提高系统的实时性和鲁棒性[9]。

1 冲击载荷下磁流变阻尼器受力分析

由于磁流变阻尼器是一个强非线性、大时滞的系统，为减小计算量，在不影响控制效果的前提下，对阻尼通道作如下假设[1-3]：

1)阻尼器的阻尼通道内始终充满不可压缩的磁流变液。

2)磁流变液在活塞工作过程中不会产生气泡。

3)磁流变体在磁流变液中不会产生沉降，且均匀分布。

4)阻尼通道沿磁极中心线对称，阻尼通道间隙的大小远小于缸体内径。

5)活塞运动时的速度和磁流变液流速有确定的数学解析关系，磁流变液流动方向与活塞运动方向平行，其他方向上没有速度分量。

当冲击载荷作用在阻尼器上时，磁流变液在压力作用下被挤入环形的阻尼通道，由于磁流变液本身具有粘性，因此，在磁流变液内部以及磁流变液与阻尼孔壁之间会产生一个和活塞运动速度成正比的粘滞性阻力F1;经流体力学分析，磁流变液在冲击载荷作用下，会由于流经的横截面突变而产生一个和活塞运动速度的平方成正比的节流阻力F2；磁流变液流动时，会因为自身质量带来的惯性，产生和活塞运动加速度成正比惯性阻力F3；同时，由于介质之间的耦合关系，会产生一个综合阻力F4，因其较小，故忽略。总阻尼力中的上述成分，均和磁流变液性质及磁流变阻尼器结构及活塞运动速度有关，这些由物质本身物理特性和运动特性决定的力属于不可控力。最后一部分是由于磁流变效应而产生的库伦阻力FMR，可以通过改变磁场电流大小进而改变磁场强度而实现阻尼力的改变，它和磁流变液的屈服应力成正比，这部分力是实现磁流变阻尼器阻尼力可控的基础[1]。

通过分析,得到磁流变阻尼器所提供的阻尼力的动力学模型为:

(1)

式中，ρ1、ρ2、ρ3、ρMR分别为各分量的比例系数，它们只与磁流变液特性以及磁流变阻尼器结构有关。

2 自动武器缓冲过程分析

设炮膛合力为Fpt，磁流变阻尼器产生的总阻尼力为FR，炮体复进时由复进簧产生的复进簧力为Ff，缓冲系统内的摩擦力为f，包括导轨上摩擦力和密封装置摩擦力等，m为武器后坐部分的质量，v为后坐时的速度，θ为射角，则在后坐过程中，有[1,2,10]：

(2)

在复进过程中，有：

(3)

对于复进簧，有：

Ff=Ff0+kx,

(4)

式中：Ff0为复进簧初力；k为弹簧刚度系数；x为位移。

因此，得出自动武器磁流变阻尼器缓冲系统动力学模型为[1]：

后坐时，

kx+f-mgsinθ)；

(5)

复进时，

ρMRτy-f-mgsinθ).

(6)

3 单神经元自适应PSD算法设计

基于单神经元PSD算法的控制器机构框图如图1所示，通过加权系数wi对输入xi进行加权，由图可知，对加权系数wi进行实时在线调整，即可实现控制器的自组织与自适应功能。

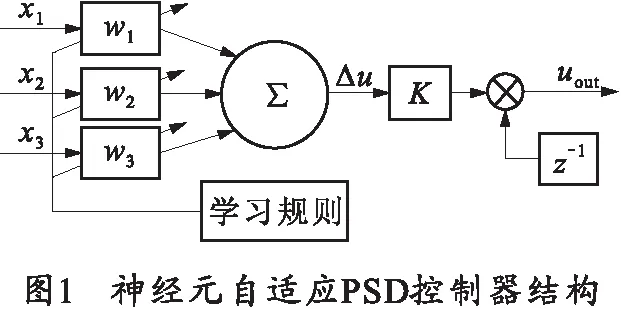
加权系数由式(7)确定：

(7)

式中：e(k)是误差反馈信号；z(k)是教师训练信号，本设计中，取z(k)=e(k)；δI为积分学习速率；δP为比例学习速率；δD为微分学习速率。

在学习过程中，为了提高系统收敛速度，可以在xi(k)1.04×xi(k-1)时，可以减小学习速率，此时，选δi(k)=0.75δi(k-1)，达到稳态后，可选δi(k)=δi(k-1).

图1中，xi作为控制器的输入，分别取作系统的误差、误差的一次差分和误差的二次差分[9]，即:

(8)

由图1得控制器的输出及学习规则可表示为[9-10]：

(9)

4 仿真和实验验证

为了验证本算法在冲击载荷下磁流变阻尼器控制中的有效性和可靠性，首先，在Simulink中进行仿真验证。仿真模型如图2所示，包括单神经元PSD控制器，阻尼器动力学模型以及冲击载荷输入3个部分，其中，利用S-Functions来实现冲击载荷和控制器两个部分。

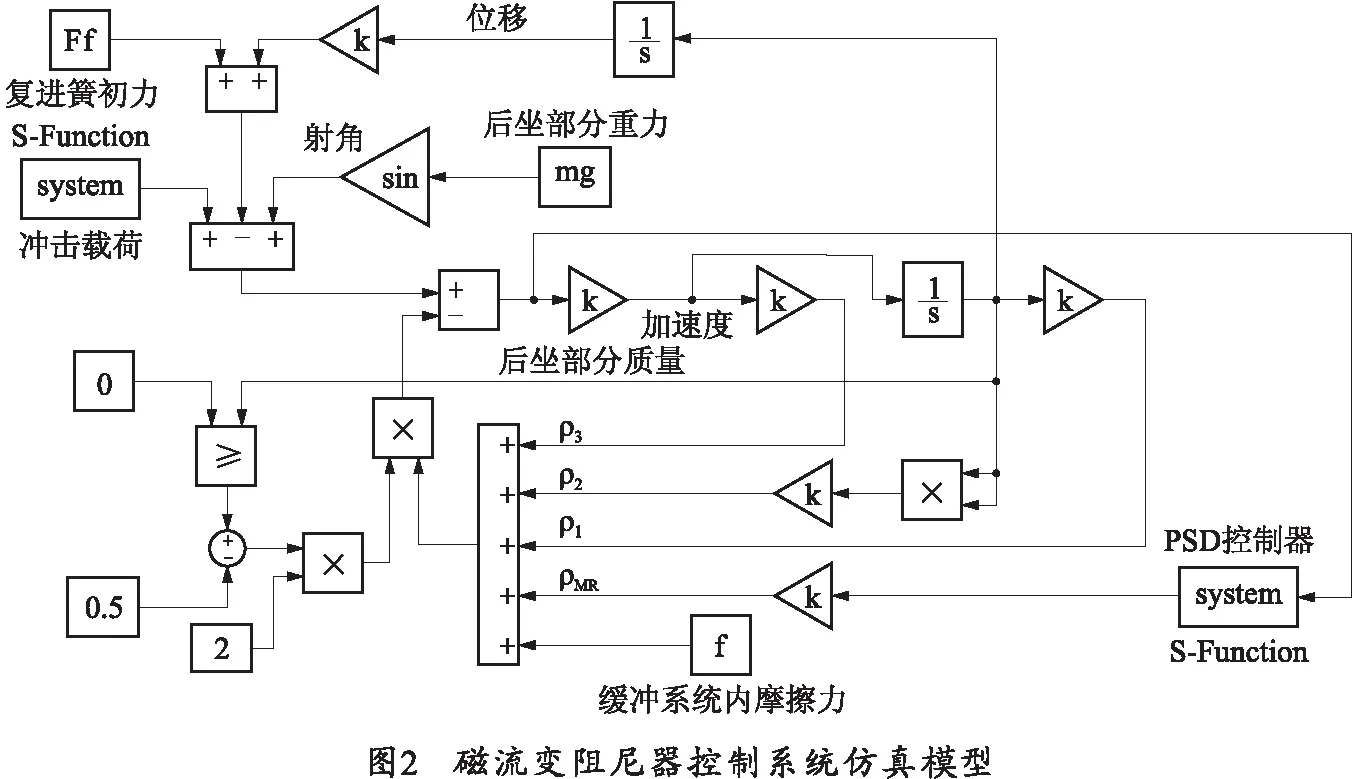
所研究的磁流变阻尼器结构参数如表1所示。

表1 磁流变阻尼器仿真系数

将表1数据带入阻尼器动力学模型，得动力学模型参数为：

ρ1=213.11,ρ2=19.25,ρ3=1.05,ρMR=0.16.

图3为控制系统的位移-时间曲线，图4为控制系统的后坐力-时间曲线。在控制算法作用下，磁流变阻尼器的最大位移为38 mm，与此同时，后坐力峰值为9.8 kN，最大超调量为1.25%.由图3、4中可以看出，在阻尼器作用下，后坐位移变化平缓，并实现了后坐力“平台”效应，表明磁流变阻尼器后坐缓冲系统具有较强的耗能减震效果，本文的PSD算法对大时滞强非线性的磁流变阻尼器具有很好的控制性能。

为进一步验证本算法对磁流变阻尼器的控制性能，搭建了由弹簧压力机、磁流变阻尼器以及控制及测量系统构成的实验平台，如图5所示。 通过控制系统向阻尼器施加不同强度的电流，观察阻尼器提供的阻尼力，来验证本算法的可行性。

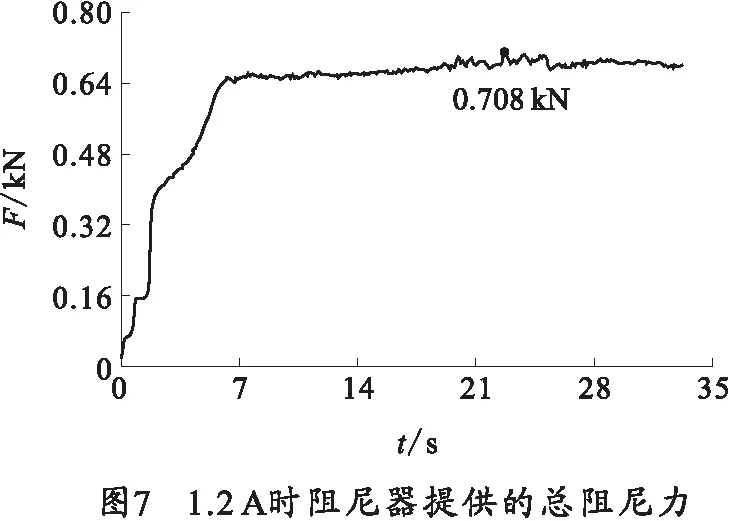
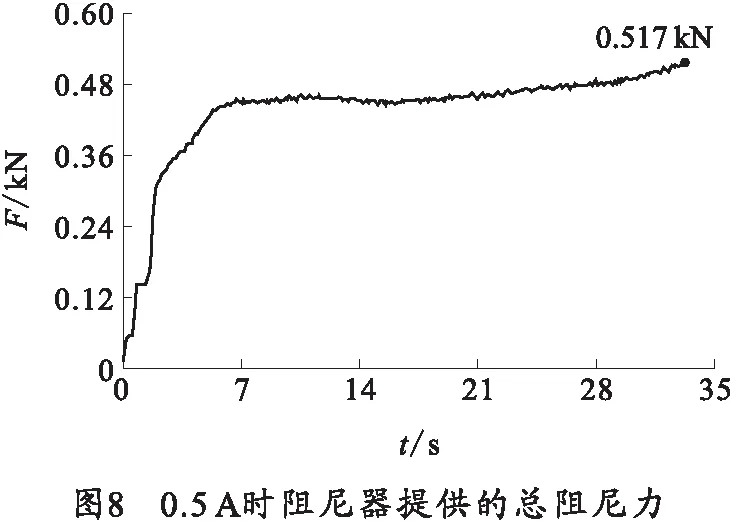
弹簧压力机上实验结果如图6～8所示。图6～8分别为1.6 A时阻尼器提供的总阻尼力，1.2 A时阻尼器提供的总阻尼力，0.5 A时阻尼器提供的总阻尼力以及阻尼力的变化过程。由图6～8中可以看出，阻尼器在冲击载荷作用下，提供的阻尼力迅速升高并很快达到稳定值，同时，随着控制器输入电流的增加，磁流变阻尼器提供的阻尼力也在升高，有效的实现了“平台”效应，并延长了“平台”的宽度。

5 结束语

为了解决自动武器缓冲后坐过程不可控的问题，笔者将磁流变阻尼器应用于自动武器缓冲控制系统。首先对阻尼器进行动力学建模，得到了对阻尼器提供的总阻尼力模型，分析了其中的可控部分，在此基础上，利用单神经元PSD控制算法鲁棒性强，算法简单，易于实现的特点，将其应用在磁流变阻尼器控制中，由仿真和实验平台验证可以看出，本算法发挥了其全局性能优越，鲁棒性强的特点，有效的实现了后坐“平台”效应，达到了满意的控制效果。

磁流变液作为新型智能材料，对它的应用研究还存在很多亟需解决的问题。国外研究证明，当磁流变液流速过快超过一定阈值，阻尼力变得不再可控，而在高射速自动武器反冲后坐过程中，这一现象必然会对后坐力的控制产生重要

影响，在以后的分析研究中，必须考虑这一效应。同时，为了简化阻尼器动力学模型，笔者将阻尼器作为单自由度系统来分析，在今后的研究中，必须考虑其在整个自动武器中的动态特性，将其放在整个缓冲后坐系统中进行整体分析。