桩周土体物理力学性质对滑坡抗滑桩桩间距的影响
张海宽,曾江波,姚文敏,耿雪峰,于 越
(1.中国地质大学(武汉) 工程学院,湖北 武汉 430074;2.深圳市勘察测绘院有限公司, 广东 深圳 518028)
抗滑桩加固是治理滑坡的重要工程措施之一,桩间距是抗滑桩设计的主要参数之一。对于抗滑桩桩间距的确定,研究人员目前主要是基于土拱效应基本理论对其进行研究。在理论分析方面,如王成华等[1]研究的主导思想是抗滑桩两侧摩擦阻力之和不小于滑坡推力,并建立了抗滑桩桩间距的计算模型,但未考虑土拱强度条件;常保平[2]主要根据土拱强度条件建立了抗滑桩桩间距的计算方法,却未考虑抗滑桩侧摩擦阻力与滑坡推力的平衡条件;周德培等[3]在常保平研究的基础上,考虑了抗滑桩桩间土摩擦力的影响,提出了一种既考虑桩间摩擦力和桩后三角形受压区受力平衡的抗滑桩桩间距计算模型;贾海莉等[4]运用极限平衡理论对抗滑桩桩间土体成拱进行研究,推导出了抗滑桩最大桩间距的计算公式;郑磊等[5]基于土拱效应,通过土拱保持整体稳定性和土拱强度条件来控制抗滑桩的桩间距;蒋良潍等[6]利用摩尔库仑强度准则,得到了抗滑桩桩间距上下限的计算公式,并将桩间土拱的计算推导到了三维模式;肖淑君等[7]首次将统一强度理论用于抗滑桩桩间距的计算;Li等[8]提出了一种三维椭球滑坡体模型,并据此模型研究发现滑坡体中心部位滑坡推力较大,而滑坡体边界部位滑坡推力相对小,治理滑坡的抗滑桩等距设置会导致资源的浪费;张海宽等[9]基于统一强度理论提出了多层滑坡体模型中抗滑桩最大桩间距的计算方法;刘涛等[10]构建了一种三维多层滑坡体模型,并提出了三维多层滑坡体中抗滑桩最小桩间距的计算方法。在试验研究方面,杨明等[14-15]基于物理模型试验探讨了抗滑桩宽度和桩间距对桩间土拱效应的影响;Ashour等[16]提供了一种评估横向荷载桩和相关曲线在完全液化土壤中响应的技术;Tang等[17]通过在渐进加载期间测试物理尺度模型来描述土桩附近的应力演化。在数值模拟方面,Liang等[11]、Chen等[12]和张建勋等[13]分别采用数值模拟方法对土拱效应进行了分析;桂蕾等[18]以万州区金金子滑坡为例,采用FLAC3D软件并结合强度折减法对该滑坡稳定性进行了数值模拟计算,并将其计算结果与极限平衡法相比较;汪洋等[19]根据新滩滑坡的地质背景和工程地质特征,建立了滑坡地质模型,并运用有限元数值模拟方法分析了其形成机理。
目前,针对抗滑桩桩间距的研究主要集中在桩周土体物理力学性质不改变的情况下对抗滑桩桩间距计算方法的优化和桩-土相互作用的分析,但桩周土体的物理力学性质同样会影响抗滑桩的桩间距。如果桩间土拱、桩后土拱因强度或平衡力不足使桩间距缩小,会导致抗滑桩数量的增加,这在一定程度上会造成施工的不便和材料的浪费,所以研究抗滑桩桩周土体物理力学性质对于桩间距的影响,并对桩周土体进行改良可以在一定程度上节省抗滑桩的施工费用。为此,本文以抗滑桩最小桩间距为例,利用解析法研究了抗滑桩桩周土体物理力学性质对桩-土相互作用平衡条件和土拱强度条件的影响,并利用数值模拟方法研究了桩周土体物理力学性质改变后对抗滑桩桩后滑坡推力分布形式的影响,从而分析了桩周土体物理力学性质对抗滑桩最小桩间距的影响;同时,针对部分渣土边坡中土体物理力学性质较差的问题,提出了渣土边坡堆积过程中在抗滑桩设桩处填筑改良土体来优化抗滑桩桩间距的方法,并对填筑土体类型、填筑范围和填筑深度进行了研究,为针对不同土体采取不同的改进方案提供了依据;此外,讨论了桩周土体物理力学性质对抗滑桩最大桩间距的影响,并将其影响结果与桩周土体物理力学性质对抗滑桩最小桩间距的影响结果进行了对比,分析了桩周土体物理力学性质对抗滑桩两种桩间距影响效果不同的原因;最后,通过深圳某渣土边坡实例应用,验证了在渣土边坡堆积过程中填筑改良土体优化抗滑桩最小桩间距方法的有效性,并对抗滑桩最小桩间距的优化效果进行分析,实例计算结果表明该渣土边坡堆积过程中在桩周位置合理填筑改良土体可以达到优化抗滑桩最小桩间距、减少施工成本的效果。
1 抗滑桩最小桩间距研究的基本理论
1.1 土拱效应
设置抗滑桩治理滑坡体时,抗滑桩附近土体在受到滑坡推力与土体抗力作用时,存在向滑坡体外移动的趋势。在抗滑桩附近土体不被挤出的情况下,不同位置土体由于受桩的作用力不同,表现出设桩处附近土体位移小、远离设桩处土体位移大的变化趋势,因土体抗剪强度的存在便会形成土拱,即土拱效应。由于土拱是土体调动自身强度抵抗外力的结果,且考虑到土体的抗压强度大于抗剪强度和抗拉强度,所以土拱的拱轴线为合理拱轴线[10]。
抗滑桩与滑坡体之间相互作用过程的研究表明[20],滑坡体转移滑坡推力荷载的方式主要有三种:一是通过桩后土拱将荷载传递给抗滑桩后壁;二是通过桩间土拱将荷载传递给抗滑桩侧壁;三是桩后土拱已经破坏后抗滑桩后壁将直接承担滑坡推力的作用。桩-土相互作用系统的三级荷载分担模型,见图1。
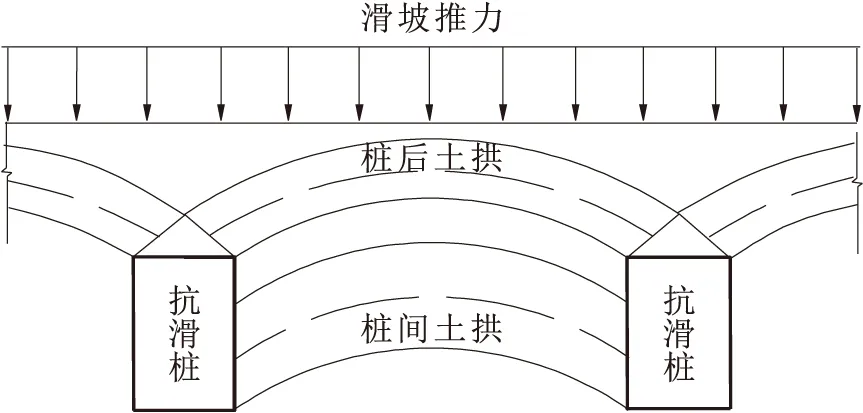
图1 桩-土相互作用系统的三级荷载分担模型[20]Fig.1 Three-stage load sharing model of pile-soil interaction system[20]
由图1可见,在抗滑桩与滑坡体之间相互作用的开始阶段最先起抗滑作用的是桩后土拱,根据此模型可计算抗滑桩的最小桩间距;随着桩间距的增大土拱变为桩间土拱,根据此模型可计算抗滑桩的最大桩间距。
1.2 基于统一强度理论的抗滑桩最小桩间距研究
张海宽等[9]、刘涛等[10]基于统一强度理论对多层滑坡体中抗滑桩合理桩间距进行了研究。与摩尔库仑强度理论相比,统一强度理论可以考虑中间主应力变化对抗滑桩最小桩间距的影响。抗滑桩最小桩间距的计算公式需要根据桩后土拱模型(见图2),并结合土拱的平衡条件和强度条件来确定。

图2 桩后土拱模型Fig.2 Soil arch model behind pile
当桩后土拱处于极限平衡状态下,平衡条件是要求桩间土体不会因为摩擦力不足而滑出,即桩后土拱与受压土体之间的摩擦力不小于相邻两桩之间的滑坡推力,根据平衡条件有[10]:
(1)
式中:参数中下角标k和i表示滑体序号,滑体k表示稳定性系数最低的滑体,滑体i表示从第一层滑体到滑体k中的某一层滑体;Nk(z)为滑体k中在距离滑体顶面深度为z处桩后三角形受压区受到的平行于拱轴线的压力(kN);qk(z)和qi(z)分别为滑体k和滑体i中在距离其顶面深度为z处的单位宽度滑坡推力(kN/m);S为抗滑桩最小桩间净距(m);αk(z)、αi(z)分别为滑体k、i桩后三角形受压区侧边与相邻桩中心点连线的夹角(°);φk为滑体k中土体的内摩擦角(°);ci、ck分别为滑体i和滑体k中土体的黏聚力(kPa);d为抗滑桩的截面宽(m);hi和hk分别为滑体i和滑体k的厚度(m);ti和tk分别为滑体i和滑体k中桩后三角形受压区侧边的边长(m);G为滑体k上层滑体提供的抗滑力(kN)。
在极限平衡状态下,研究抗滑桩最小桩间距时需要保证抗滑桩周围土体的三角形受压区发挥作用,根据图2有[10]:
Nk(z)cotαk(z)=Nk(z)tanφk+cktk
(2)
土拱强度条件是要求土拱不因为强度不够而发生破坏,基于统一强度理论有[10]:
(3)
式中:b为中间主应力参数,根据肖淑君等[7]的研究,其取值范围为0.2~0.7,无单位;σkz(z)为滑体k内深度为z处土体的自重应力(kPa)。
结合公式(1)~(3),有[10]:
l=S+d
(4)
式中:l为相邻抗滑桩中心距(m);Nk(z)和αk(z)的计算公式如下[10]:
(5)
2 桩周土体物理力学性质对抗滑桩最小桩间距的影响
2.1 桩周土体物理力学性质对桩后土拱强度条件的影响分析
桩后土拱是由土体抵抗滑坡推力时调整自身强度形成的,桩后土体不同会直接导致土体的物理力学性质的不同,进而使土拱自身强度发生改变,所以适当改变桩后三角形受压区土体的物理力学性质可以提高土拱的强度,从而对抗滑桩的最小桩间距进行优化。通过对公式(3)进行变换,可得到:
(6)
式中:tk为关于土拱土体物理力学性质参数ck、φk的函数,在此讨论土体物理力学性质变化对于土拱拱脚处压力Nk(z)的影响时,假设bσkz(z)/(1+b)=100 kN/m2、d=1.8 m,根据《工程地质手册》[21]中土体物理力学性质参数的变化范围,首先固定土拱土体内摩擦角φk取值为20°,黏聚力ck取值范围为0~80 kPa,得到Nk(z)与ck的关系曲线[见图3(a)];同样固定土拱土体的黏聚力ck取值为10 kPa,内摩擦角φk取值范围为10°~40°,得到Nk(z)与φk的关系曲线[见图3(b)]。

图3 桩后土拱土体物理力学性质参数对土拱拱脚处 压力Nk(z)的影响Fig.3 Influence of physical and mechanical properties of soil under the piles on the pressure at the arch foot of the soil arch
由图3可见,当组成土拱土体的黏聚力越大时,土拱承受滑坡推力的能力越大;当组成土拱土体的内摩擦角越大时,土拱承受滑坡推力的能力越小。
2.2 桩周土体物理力学性质对桩-土相互作用平衡条件的影响分析


图4 桩后三角形受压区土体物理力学性质参数对 抗滑桩最小桩间净距S的影响Fig.4 Influence of physical and mechanical properties of soil on the minimum pile spacing in the post-triangle compression zone
由图4可见,桩后三角形受压区土体的黏聚力对抗滑桩最小桩间净距S的影响不是单调的,在土体黏聚力值较小和较大时抗滑桩的最小桩间净距S均较大,而抗滑桩的最小桩间净距随着三角形受压区土体内摩擦角φk的增大而减小。
2.3 桩周土体物理力学性质对桩后滑坡推力分布形式的影响分析
上述讨论的是在同一深度处不同范围内桩后土体物理力学性质变化对抗滑桩桩间距的影响,而在不同深度处桩后土体物理力学性质的变化也会影响滑坡推力的分布形式,从而影响抗滑桩的桩间距。因此,合理地改变桩后滑坡推力的分布形式可以达到优化抗滑桩最小桩间距的目的。戴自航[22]研究发现桩后滑坡推力的分布形式会随着土体物理力学性质的改变而改变,但是该研究都是基于滑坡土体为均质土体的情况下进行的。本文将以《工程地质手册》[21]中的砂土和黏土为例,研究桩周土体对桩后滑坡推力分布形式的影响,其中砂土的主要物理力学性质参数φ为42°、c为2 kPa、密度为2.05 g/m3,黏土的主要物理力学性质参数φ为17°、c为41 kPa、密度为1.85 g/m3。研究过程可分为滑体土体与桩周土体相同(第一类土体组合)和滑体土体与桩周土体不相同(第二类土体组合)两类。首先,研究第一类土体组合对于桩后土体滑坡推力分布形式的影响,即在FLAC3D软件中建立长130 m、高68 m、宽10 m的抗滑桩与滑坡的数值计算模型[见图5(a)],其中设桩处滑体厚度为8 m,抗滑桩设桩前壁距离坡脚为27 m,抗滑桩选择截面为2 m×3 m的类型,桩间距为4 m,通过输入相应参数,可得到土体组合均为砂土的桩后滑坡推力分布曲线[见图6(a)]、土体组合均为黏土的桩后滑坡推力分布曲线[见图6(b)]。然后,研究第二类土体组合对于桩后土体滑坡推力分布形式的影响,即在FLAC3D软件中建立长130 m、高68 m、宽10 m的抗滑桩与滑坡的数值计算模型[见图5(b)],其中滑体厚度和抗滑桩设桩位置与第一类土体组合相同,抗滑桩选择截面为2 m×3 m的类型,桩间距为4 m,在抗滑桩四周设置宽1 m的置换桩周土层,将土体为砂土的滑体中桩周土体置换为黏土,得到置换后滑体的桩后滑坡推力分布曲线[见图6(a)],观察到这种情况下滑坡推力的分布形式与滑体土体为黏土的桩后滑坡推力分布形式相似。将土体为黏土的滑体中桩周土体置换为砂土,得到置换后滑体的桩后滑坡推力分布曲线[见图6(b)],观察到这种情况下滑坡推力的分布形式与滑体土体为砂土的桩后滑坡推力分布形式相似。通过观察图6(a)、6(b)中的滑坡推力分布曲线可以看出,滑体的桩后滑坡推力分布形式与置换土体后滑体的桩后滑坡推力分布形式较为相似。

图5 抗滑桩与滑坡的数值计算模型Fig.5 Numerical calculation model for anti-slide piles and landslide

图6 不同土体组合的桩后滑坡推力分布曲线Fig.6 Thrust distribution diagram of landslide behind pile under different soil combination conditions
3 填筑土体对抗滑桩最小桩间距的影响
3.1 桩周土体的填筑类型
渣土边坡是一种由于人类活动形成的渣土混合体边坡,随着我国地下工程的迅猛发展,越来越多的渣土边坡出现在人类生活区域,渣土边坡的失稳会对人民群众的生命和财产安全造成严重影响,如2015年12月20日在广东深圳某渣土受纳场发生的大规模滑坡事故,造成77人死亡、33栋房屋被毁[23]。抗滑桩支护是加固治理边坡最为广泛的工程技术措施,而桩间距是设计抗滑桩的主要参数之一,但部分渣土边坡土体的物理力学性质较差,抗滑桩的桩间距较小,而渣土边坡堆积过程中在抗滑桩桩周位置填筑改良土体可以合理地优化桩间距。
由第2.1节和2.2节对相邻两抗滑桩桩间土体物理力学性质的研究显示,土体物理力学性质的改变对桩周三角形受压区及桩间土拱的影响不同。在同一深度处,桩周三角形受压区填筑土体应尽量选择黏聚力较大或较小、内摩擦角较小的土体,而桩间土拱填筑土体应选择黏聚力较大、内摩擦角较小的土体。
根据第2.3节分析可知,当桩后土体改变时抗滑桩桩后滑坡推力的分布形式也会发生改变,桩后土拱承受滑坡时,土拱拱脚将所受压力通过三角形受压区传递给抗滑桩,在同一土体中土体自重应力与深度成正比关系,所以根据公式(3)在其他参数不变的情况下深度与桩间土拱能承受的滑坡推力呈递增一次函数关系,在研究深度与桩后土拱滑坡推力分布形式同时变化对抗滑桩桩间距的影响时,对公式(4)进行数学变化,得到单桩承载力计算公式如下:
(7)



图7 单桩所受滑坡推力随深度的变化曲线Fig.7 Curve of landslide thrust with depth in a single pile
3.2 桩周土体的填筑范围
桩周不同位置需要填筑的土体类型不同,所以在填筑土体时应确定不同类型土体的填筑范围。桩后三角形受压区桩周土体的填筑范围,可根据填筑后土体的物理力学性质并结合公式(7)确定桩后三角形受压区侧边与相邻两桩中心点连线的夹角,然后通过三角函数关系和桩长确定。
由于土拱位置未知,但土拱轴线与相邻两桩中心点连线的夹角由拱脚位置向对称中心不断减小,所以桩后土拱处于桩后土体置换区,见图8。
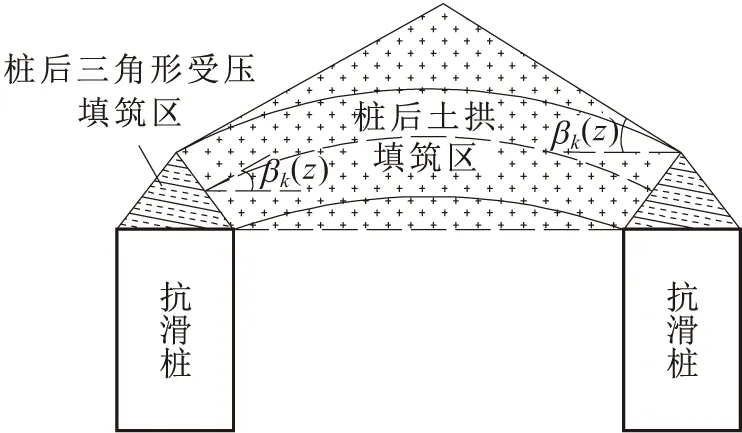
图8 桩后土体置换区示意图Fig.8 Diagram of soil replacement area behind piles注:βk(z)为三角形受压区侧边与拱脚处轴线切线的夹角(°),与αk(z)互余。
填筑面积的计算公式如下:
(8)
填筑改良土体时存在一个深度,在这个深度利用原渣土边坡土体物理力学性质参数计算得到的抗滑桩最小桩间距等于填筑改良土体后确定的抗滑桩最小桩间距,该深度称为填筑土体临界深度,在填筑过程中仅需对该深度以下部分填筑改良土体。此处所指的填筑为渣土边坡机械堆积过程中对抗滑桩周围填筑优良土体,而不是渣土边坡堆积完成后对抗滑桩周围土体进行置换。影响桩后滑坡推力分布形式的桩后土体置换范围还有待于通过试验做进一步的研究,在这里不做讨论。考虑到渣土边坡一般为机械分层施工,对填筑区填筑不同土体会造成施工不便,所以可以选择黏聚力较大、内摩擦角较小的土体进行整体填筑。
4 实例应用与分析
为了进一步分析桩周土体对抗滑桩最小桩间距的影响,本文通过引入深圳某渣土边坡实例,用来验证在桩周填筑改良土体优化抗滑桩最小桩间距方法的有效性和实用性。
4.1 某渣土边坡概况
深圳市某渣土边坡场地原始地貌为丘陵,因场地大规模的人工堆填余泥渣土,现状地形已发生巨大的改变,总体上场地处于山顶,场地中间地形较为平缓,大致呈自东向西倾伏,在西侧、南侧及北侧边缘顺接原来冲沟的位置设置了人工渣土边坡,地势相对较低,边坡总长约210 m,坡高约为40 m,边坡后缘高程为102 m,前缘高程为60 m,高差达42 m,该渣土边坡剖面图见图9。

图9 深圳某渣土边坡剖面图Fig.9 Section of a slag slope in Shenzhen

4.2 桩周土体物理力学性质对抗滑桩最小桩间距的影响分析
由于实例为一层滑体边坡,所以变量中去掉了表示滑体层数的下标。首先利用GEO-Studio数值软件确定该渣土边坡滑动面的位置(见图9中红线所示),并取抗滑桩设计的安全系数为1.15,计算得到设桩位置处滑坡推力为P=713.24 kN/m。
不进行桩周土体置换的情况下,根据戴自航[22]的研究,滑坡推力的分布形式为梯形分布,将滑体参数带入公式(4)、(5)中,计算得到抗滑桩的最小桩间距(l)为3.85 m,该值小于该滑坡设计的抗滑桩桩间距(为4 m)但相差不大,这说明该计算结果是合理的。

图10 深圳某渣土边坡中单桩所受滑坡推力随深度 的变化曲线Fig.10 Curve of landslide thrust with depth in a single pile in a slag slope in Shenzhen
根据前述研究可知,应尽量选择黏聚力较大、内摩擦角较小的土体填筑在抗滑桩附近以达到优化抗滑桩最小桩间距的目的。该边坡中单桩所受滑坡推力随深度的变化曲线见图10,且边坡土体的桩后滑坡推力分布形式为梯形分布,所以不用调整影响桩后滑坡推力分布区的土体。考虑到渣土边坡填筑为机械分层填筑,所以填筑改良土体区应该选择同一种土体,根据《工程地质手册》[21]选择在桩后土拱填筑区和桩后三角形受压填筑区填筑c为68 kPa、φ为20°、密度为1.95 g/m3的黏土,并结合公式(1)~(5)计算出抗滑桩的最小桩间距为6.63 m。考虑到施工情况,填筑范围为抗滑桩后壁向后的4.53 m,填筑深度为4~13.7 m。
改良土体的填筑只需要在渣土边坡堆积过程中,在抗滑桩后壁向后的4.53 m,填筑深度为4~13.7 m的范围内填筑c为68 kPa、φ为20°的黏土即可,无需增加其他工序,施工难度和成本几乎不变,所以可以通过此种方法来改良渣土边坡抗滑桩的最小桩间距,减少设桩期间开挖土体的体积,从而达到优化抗滑桩的最小桩间距、降低施工成本的目的。
5 讨 论
本文重点研究了渣土边坡堆积过程中填筑桩周改良土体对抗滑桩最小桩间距的影响,本节将研究桩周土体物理力学性质对抗滑桩最大桩间距的影响。
5.1 桩周土体物理力学性质对抗滑桩最大桩间距的影响分析
5.1.1 抗滑桩最大桩间距的计算
抗滑桩最大桩间距的计算需要基于桩间土拱模型,见图11。根据张海宽[9]、刘涛等[10]的研究,抗滑桩最大桩间距的计算模型和计算过程与抗滑桩最小桩间距的基本相似。根据土拱强度条件,有:
(9)

根据土拱平衡条件,有:
(10)
式中:S′为最大桩间净距,即相邻抗滑桩临近侧边的距离;G′为上方滑体与抗滑桩的相互作用力(kN);T为抗滑桩的截面长度(m)。
若桩侧三角形受压区发挥作用,则有:
(11)
结合公式(9)至(11),有:
(12)
式中:l′为抗滑桩的最大桩间距,即相邻两抗滑桩桩中心点的距离(m)。

图11 桩间土拱模型Fig.11 Soil arch model between piles
5.1.2 桩周土体物理力学性质对桩间土拱强度条件的影响分析


图12 桩间土拱土体物理力学性质参数对土拱拱脚处 压力的影响Fig.12 Influence of physical and mechanical properties of soil arch between piles on pressure at the foot of soil arch

5.1.3 桩周土体物理力学性质对桩-土相互作用平衡条件的影响分析
当抗滑桩桩侧三角形受压区土体物理力学性质发生改变时,土拱的平衡条件也会发生改变,从而影响抗滑桩的最大桩间距。假设抗滑桩尺寸为T=3 m、d=2 m,其他参数利用2.2节中的假设,结合公式(12)可得到桩侧三角形受压区土体物理力学性质参数改变后对抗滑桩最大桩间净距的影响,见图13。

图13 桩侧三角形受压区土体物理力学性质对抗滑桩 最大桩间净距的影响Fig.13 Influence of soil physical and mechanical properties on pile spacing in pile-side triangular compression zone
通过对比图4与图13发现,桩侧三角形受压区土体物理力学性质参数改变后对抗滑桩最大桩间距的影响与桩后三角形受压区土体物理力学性质参数改变后对抗滑桩最小桩间距的影响不同,桩侧三角形受压区土体的黏聚力和内摩擦角越大,计算得到的抗滑桩最大桩间净距S值越大。
5.3 桩周土体物理力学性质对抗滑桩最大和最小两种桩间距影响不同的原因分析
通过对比发现,桩周土体中土拱土体物理力学性质参数的改变对抗滑桩的最大桩间距和最小桩间距的影响效果相同,而桩周三角形受压区土体物理力学性质参数的改变对抗滑桩最大和最小两种桩间距的影响效果不同,其原因是桩周土体物理力学性质参数的改变会直接影响应力的大小,同时也会影响桩周土体受压区面积从而影响抗滑桩桩间距的大小。抗滑桩最大桩间距和最小桩间距的土拱强度计算公式大致相同,所以在土拱区土体物理力学性质改变时两者拱脚处受压的变化趋势相同。但是抗滑桩最大桩间距和最小桩间距的平衡条件计算公式不同,通过公式(1)发现抗滑桩的最小桩间距计算中黏聚力发挥平衡作用同样受桩后三角形受压区的影响,而通过公式(10)发现抗滑桩的最大桩间距计算中黏聚力发挥平衡作用只受抗滑桩侧边长T的影响,与桩侧三角形受压区无关。
6 结 论
(1) 本文以抗滑桩最小桩间距为例,通过解析法研究了桩周土体物理力学性质对于土拱强度条件和桩-土相互作用平衡条件的影响,并利用数值模拟的方法研究了桩周土体物理力学对桩后滑坡推力分布形式的影响。
(2) 以渣土边坡堆积过程中在设桩位置处填筑改良土体为例,研究了填筑土体类型、填筑范围和填筑深度对抗滑桩最小桩间距的影响,为合理优化抗滑桩最小桩间距提供了一定的理论依据。
(3) 通过对深圳某渣土边坡实例的计算,提出了渣土边坡多种堆积过程中填筑改良土体的方法,并对填筑效果进行了分析,结果表明:在不增加施工难度和施工成本的基础上,在渣土边坡堆积过程中填筑改良土体的抗滑桩最小桩间距优化方法有一定的实际意义。
(4) 讨论了桩周土体物理力学性质对抗滑桩最大桩间距计算过程中土拱强度条件和桩-土相互作用平衡条件的影响,并将其影响结果与桩周土体物理力学性质对抗滑桩最小桩间距的影响结果进行了对比,分析了桩周土体物理力学性质对抗滑桩两种桩间距影响不同的原因。

