基于无量纲数的PCA-MRA在煤矿瓦斯涌出量预测中的应用
金洪伟,周 捷
(西安科技大学安全科学与工程学院,陕西 西安 710054)
近年来,综合机械化的采煤方式在我国得到了不断推广,此方式虽增加了掘进效率,但也增加了巷道中的瓦斯涌出量,为瓦斯爆炸等事故的发生埋下了隐患。因此,煤矿瓦斯涌出量的准确预测对井下安全生产具有重要作用[1]。20世纪80年代,俄罗斯学者首次提出在采煤时须进行瓦斯涌出量预测;英国学者Greedya[2]首创艾黎法,基于时间和开采技术来预测煤矿瓦斯涌出量。我国最先提出的第一类传统的煤矿瓦斯涌出量预测方法是基于数据统计分析的矿山统计法,如1959年煤科总院抚顺分院第一次在淮南矿务局谢家集二矿应用矿山统计法预测了深部矿井瓦斯涌出量[3]。第二类传统的煤矿瓦斯涌出量预测方法是分源预测法,如戴永禄[4]应用分源预测法预测了煤层瓦斯涌出量,并将该法与趋势面法进行了对比;李晓华等[5]运用分源预测法实现了煤矿瓦斯涌出量的动态分析;张占国等[6]提出利用分源预测法预测经“立体”预抽瓦斯方法治理后的煤层瓦斯涌出量。但是,由于煤层地质条件和自然因素的不同,这两类传统的煤矿瓦斯涌出量预测方法在实际操作中具有一定的局限性。瓦斯地质数学模型法是近年来国内外学者提出的一种新的煤矿瓦斯涌出量预测方法,该方法通过建立包括原始瓦斯含量、煤层厚度等在内的多参数数学模型来预测煤矿瓦斯涌出量,如张子戌等[7]首次提出利用瓦斯地质数学模型法来预测矿井瓦斯涌出量。此外,Dong[8]提出了瓦斯排放时间序列方法,并将其作为回归函数建立了高斯过程回归模型,结果表明该方法的预测结果准确、可靠;董晓雷等[9]提出利用最小二乘支持向量机(LS-SVM)方法来预测煤矿瓦斯涌出量;Li等[10]分析了煤矿瓦斯涌水量的复杂非线性特征,提出了基于自组织数据挖掘的煤矿瓦斯涌水量预测方法;景国勋等[11]研究认为对于基本符合线性规律的数据,灰色模型较一元线性回归模型对煤矿瓦斯涌出量的预测精度更高;Liang等[12]提出在考虑瓦斯涌出源以及流固耦合过程的条件下,通过建立动态瓦斯预测模型来对煤矿瓦斯涌出量进行预测将具有更高的准确性;Booth等[13]研究认为现有的瓦斯排放预测的局限性,可以通过改进的空间数据集得出的预测结果以及包含基本物理和能量相关原理的技术来解决。
综上研究可知,近年来运用瓦斯地质数学模型法来预测煤矿瓦斯涌出量的预测方法已成为主要发展趋势,多因素分析会为煤矿瓦斯涌出量预测提供丰富的信息,但由于所选参数的量纲不一致,会使监控数据不具可比性,从而导致预测精度低,且也增加了问题的复杂性,给分析带来不便。因此,如何科学、合理地将多因素整合为较少的几个因素,并消除量纲的影响,对提高预测精度至关重要。针对上述问题,本文采用无量纲数据并运用主成分分析与多元回归分析相结合的方法来预测煤矿瓦斯涌出量。
1 主成分分析法及其在R语言中的模型构建
1.1 主成分分析法的基本原理
主成分分析(Principal Component Analysis,PCA)是利用降维的思想,将多个变量以线性组合的形式转化为少数几个综合变量(即主成分),各主成分之间相互独立,并具有反映变量的绝大部分信息的能力。该方法不但克服了单一指标不能准确预测煤矿瓦斯涌出量变化趋势的问题,而且将复杂的影响因素简化为几个主成分,实现了降维分析,并简化了复杂问题,能得到更为科学、准确的预测信息。
1.2 R语言主成分分析法的基本步骤
R语言主成分分析法的基本步骤[14]如下:
(1) 求得相关系数矩阵:采用相关系数矩阵进行主成分分析。
(2) 提取主成分:采用R语言中的psych包对相关系数矩阵提取主成分,本文要求主成分对变量的解释率达到90%以上,由此决定提取的主成分个数。
(3) 主成分旋转:采取Varimax最大方差正交旋转法进行主成分旋转。
(4) 获取主成分得分:利用主成分旋转后得到的主成分得分系数矩阵A与无量纲化处理后的原始数据转置后形成的矩阵B相乘,求得主成分得分。
1.3 主成分分析法在R语言中的模型构建
R语言是一款应用比较广泛且允许进行二次开发的编程语言,主要应用于统计学上相关的分析计算,并且可以很直观地将分析计算结果展现于命令窗口。由于主成分分析中很多的理论分析可以较容易地利用R语言来实现,并且利用R语言建立主成分分析预测模型的操作过程简便、灵活,因此本文选择R语言作为模型建立的工具。
本文通过对煤矿瓦斯涌出量的影响因素进行分析,选用文献[15]中某煤矿18个月收集到的18组瓦斯涌出量以及各影响因素原始数据作为分析对象,其中第1~10组数据为试验数据,第11~18组数据为验证数据,详见表1。

表1 某煤矿瓦斯涌出量以及各影响因素原始数据统计表
在多指标评价体系中,由于各评价指标的性质不同,通常具有不同的量纲,如果直接采用原始数据进行分析,当各指标间的数值相差较大时,就会突出数值较高的指标在综合分析中的作用,相对削弱数值较低指标的作用。因此,为了保证结果的准确性,需要对各影响因素数据进行无量纲化处理,从而解决数据的可比性问题。本文采用数据标准化中的正规化方法对各影响因素数据进行无量纲化处理,即对每列数据x1,x2,…,xn进行变换:
其中:
某煤矿瓦斯涌出量以及各影响因素经无量纲化处理后的原始数据见表2。

表2 某煤矿瓦斯涌出量以及各影响因素经无量纲化处理后的原始数据统计表
首先,依据第1.2节R语言主成分分析法的步骤,采用R软件psych包中的principal()函数进行主成分分析,其分析结果见表3。
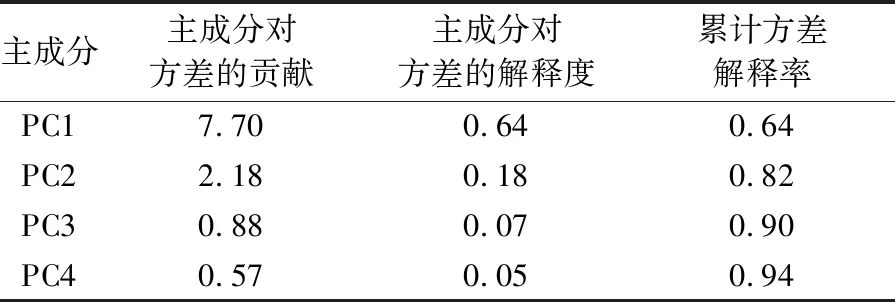
表3 主成分分析结果统计表
注:PC为旋转之前的主成分。
由表3可见,在提取4个主成分后,所提取的主成分因子的累计方差解释率可达90%以上。
然后,采用R软件中的Varimax最大方差正交旋转法进行主成分旋转,目的是使一系列主成分载荷矩阵变得更容易解释,尽可能对主成分数据去噪,使得每个主成分只由一组有限的变量来解释。表4为主成分经旋转后各项指标的得分值。
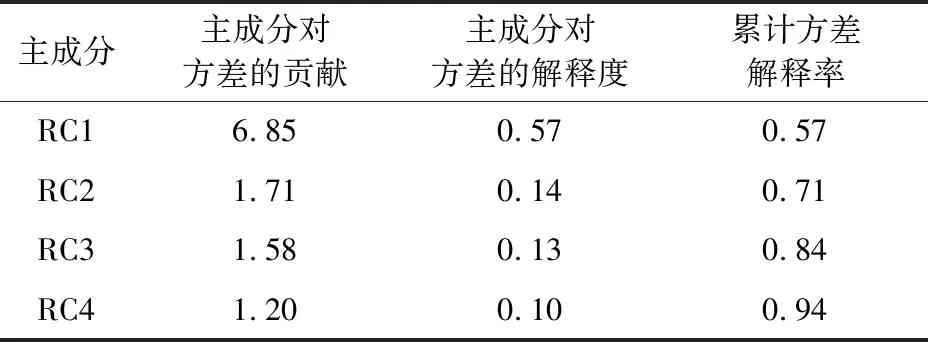
表4 主成分旋转后结果统计表
注:RC为旋转之后的主成分。
对比表3和表4可知,主成分经旋转后的累计方差解释率没有发生变化(94%),只有各主成分对方差的解释度发生了改变,使各主成分的方差解释度最大程度地趋于相同,起到了主成分数据去噪的作用。
最后,利用principal()函数中的“score=TRUE”命令,得到各主成分的得分系数,见表5。

表5 主成分的得分系数
由表5可见,主成分1主要包括煤层原始瓦斯含量、煤层埋藏深度、煤层厚度、推进速度、采高、采出率和开采强度;主成分2主要包括煤层倾角和邻近层厚度;主成分3主要包括邻近层层间距和工作面长度;主成分4包括邻近层瓦斯含量。
综上分析可见,主成分分析降低了煤矿瓦斯涌出量影响因素的维数,从而减少了后续多元回归模型计算输入变量的个数,降低了建立煤矿瓦斯涌出量预测模型的难度,同时保留了原始指标数据94%的信息,为更准确地预测煤矿瓦斯涌出量提供了保障。
2 煤矿瓦斯涌出量的多元回归预测
经第1.2节R语言主成分分析法步骤(4)的运算,即将主成分旋转后得到的主成分得分系数矩阵A(见表5)与无量纲化处理后的原始数据(见表2)转置后形成的矩阵B相乘,得到各主成分得分数据, 见表6。 其中,第1~14组数据为试验数据, 第15~18组数据为验证数据。本文采用多元回归分析作为煤矿瓦斯涌出量的预测方法,如多元线性函数、多元幂函数、多元指数函数、多元对数函数[16]等,并利用MATLAB软件对各主成分得分进行多元回归分析,通过比较标准差(RMSE)和决定系数(R2)来选取煤矿瓦斯涌出量与各主成分之间的最优函数关系式,各种形式函数关系式的拟合结果见表7。

表6 主成分得分数据统计表

表7 某煤矿瓦斯涌出量与各主成分之间的函数关系式拟合结果
由表7可知, 多元线性函数关系式的决定系数R2最高(0.988)、标准差RMSE最小(0.189),因此得到煤矿瓦斯涌出量与各主成分之间的最优函数关系式为
y=5.49+0.29F1-0.15F2+0.10F3-0.007F4
采用上述多元线性函数关系式,并根据表6中各组验证数据对某煤矿瓦斯涌出量进行预测,其预测结果及其相对误差见表8。
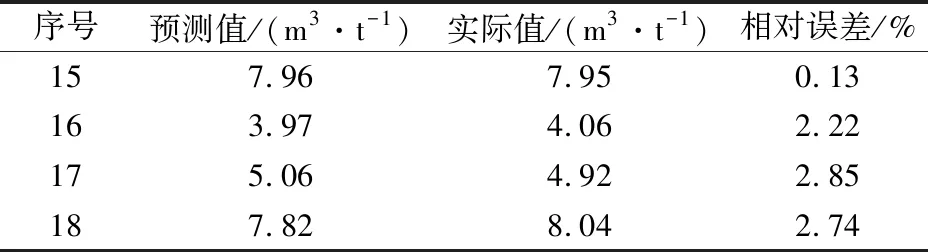
表8 某煤矿瓦斯涌出量预测结果及其相对误差
由表8可知,在4组验证数据中,某煤矿瓦斯涌出量的预测值与实际值的相对误差最小值为0.13%,最大值为2.85%,平均值为1.99%,4组验证数据的相对误差均在3%以下,表明该预测模型的预测精度较高。
由于井田地质构造等客观因素的影响,其预测结果会不可避免地偏离实际值,但本文建立的煤矿瓦斯涌出量预测模型的预测误差在合理范围内,表明该方法可以作为煤矿瓦斯涌出量的预测方法。
3 结 论
(1) 本文提出对影响煤矿瓦斯涌出量各主要因素进行无量纲化处理的方法,该方法使用无量纲量来描述客观规律,解决了数据量纲不一而使监测数据不具可比性、且导致预测精度低的问题。
(2) 主成分分析法能有效地将众多煤矿瓦斯涌出量的影响因素进行降维简化,将原始数据中的12个指标简化为4个主成分,该方法大大减少了建立预测模型时输入影响因素的数量,降低了建模时的难度。
(3) 经过主成分分析后得到的4个主成分,其中主成分1包括煤层原始瓦斯含量、煤层埋藏深度、煤层厚度、推进速度、采高、采出率和开采强度;主成分2包括煤层倾角和邻近层厚度;主成分3包括邻近层层间距和工作面长度;主成分4包括邻近层瓦斯含量。经主成分分析选取的煤矿瓦斯涌出量预测指标,包含了原始数据样本90%以上的信息,从而保障了煤矿瓦斯涌出量预测模型的准确建立。
(4) 经计算,在4组验证数据中,某煤矿瓦斯涌出量的预测值与实际值的相对误差最小值为0.13%,最大值为2.85%,平均值为1.99%,表明原始数据经无量纲化处理后,采用主成分分析与多元线性回归分析相结合的方法构建的煤矿瓦斯涌出量预测模型的预测精度较高。

