滚动轴承寿命动态预测新方法*
孟文俊 , 张四聪, 淡紫嫣, 蒋 端, 刘 弹, 徐光华,2
(1. 西安交通大学机械工程学院 西安,710049) (2. 西安交通大学机械制造系统工程国家重点实验室 西安,710054)
引 言
在机器运行过程中,一旦机械设备的某个零部件发生故障,往往会影响整个机械设备的性能,有可能造成巨大的经济损失。滚动轴承性能和可靠性对整个机械设备的可靠运行起着至关重要的作用[1]。随着滚动轴承寿命理论研究的不断发展,寿命预测方向已经具有非常成熟的理论基础和较丰富的实践应用。根据滚动轴承寿命预测模型的不同,预测方法分为以下3种类型[2]:基于概率论的寿命预测方法、基于断裂力学的寿命预测方法和基于模型的寿命预测方法。其中基于模型的寿命预测方法具有建模简单、(易于操作的优点,被广泛应用。Gebraeel等[3]将历史退化过程的性能数据采用反向传播算法(back propagation,简称BP)的神经网络进行训练,然后把当前运行部件的性能数据输入神经网络中进行学习,通过与历史数据的差异估计当前部件的退化轨迹,最后通过Bayes法对部件的剩余寿命进行预测,该方法对滚动轴承寿命的预测也适用。Sun等[4]利用支持向量机建立了轴承的寿命预测模型,进行了滚动轴承寿命的预测。申中杰等[5]以均方根值为特征指标,结合多变量支持向量机预测滚动轴承剩余寿命。Ali等[6]提出了基于简化自适应谐振神经网络(simplified fuzzy adaptive resonance theory map,简称SFAM)神经网络和Weibull分布的寿命预测模型。文献[7]将改进的指数模型用于滚动轴承寿命预测,可以有效减少预测误差。王奉涛等[8]提出基于基于核主分量分析(kernel principal component analysis,简称KPCA)和威布尔比例故障率模型(Weibull proportional hazards model,简称WPHM)的方法,可以反映滚动轴承退化过程。
虽然基于模型的寿命预测方法占主导地位,但该方法依据样本数据变化的特点进行建模,对样本的完善程度和质量有较高要求,且会受到各种假设条件的约束。其通过估计结构和参数确定的模型不会随滚动轴承运行时间的增加而发生变化,是一种静态模型,而运行性能可靠性分析是在滚动轴承运行过程中进行分析,是动态问题。本研究通过PCA方法对滚动轴承的多个性能指标进行融合,构建了能有效反映滚动轴承退化过程的衰退性能指标,进行寿命预测。通过相空间重构技术实现当前退化过程和历史退化过程的对比,得到寿命预测值。同时,结合历史失效时间进行统计推断,得到更准确的平均寿命,并随着观测样本的不断积累实现平均寿命的动态更新。
1 滚动轴承衰退性能指标的建立
笔者选用PCA技术进行多特征融合,该衰退性能指标建立的流程如图1所示。
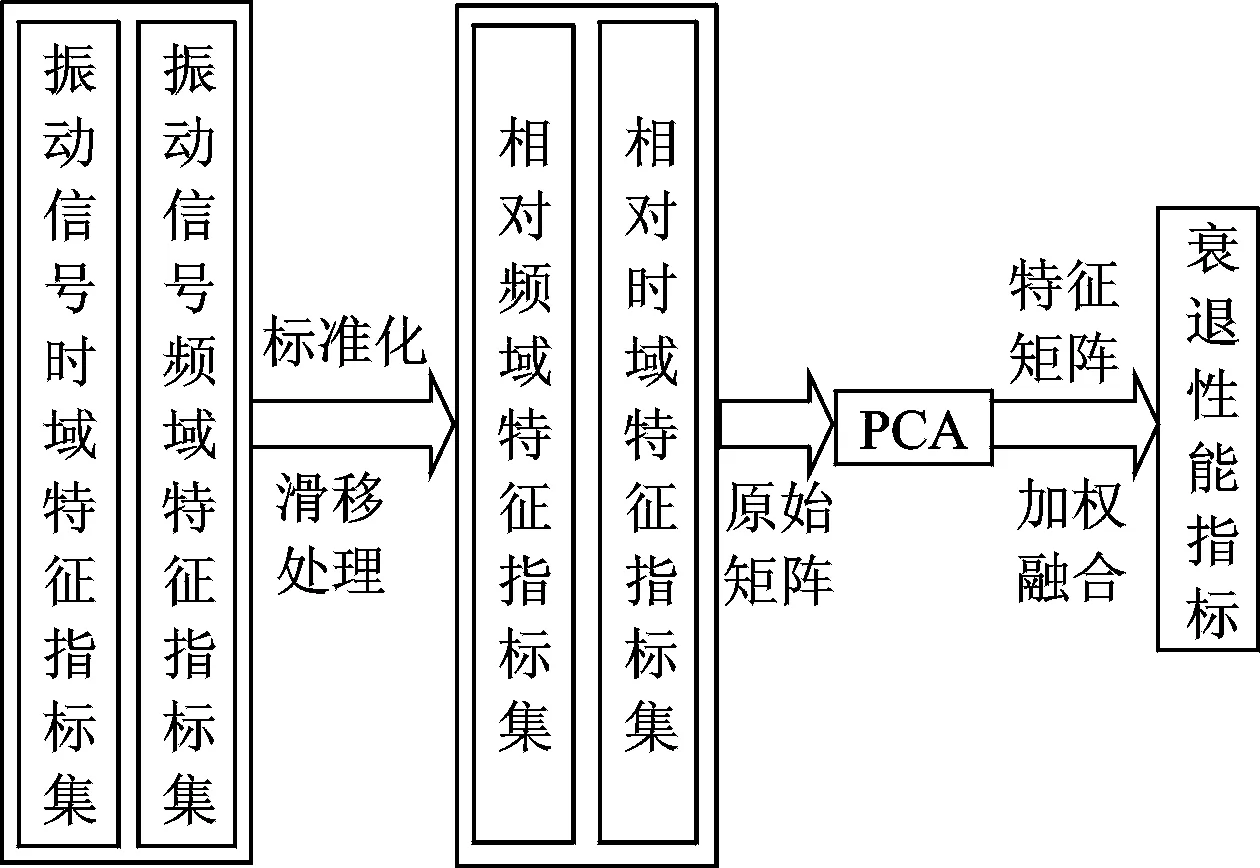
图1 衰退性能指标构造流程Fig.1 Construction procedure of fading performance index
1.1 滚动轴承时域和频域特征提取
时域指标包括有量纲指标和无量纲指标,前者对早期故障较为敏感,但不稳定;后者不受滚动轴承转速和载荷的影响,对信号幅值和频率的变化不敏感,会随故障的发展敏感性下降。
频域特征指标如表1所示,s(k)为信号x的频谱,k=1,2,…,K,K为谱线数。fk为第k条谱线的频率值,其中:频率特征p1反映了频域振动幅值变化;p2~p4,p6,p10~p13反映了频谱的分散或集中程度;p5,p7~p9反映了主频带位置的变化。
1.2 滚动轴承相对特征指标的建立
为了减少不同轴承之间的差异,在特征融合之前对特征指标进行标准化和滑移处理。任意选取正常期内一段趋势平稳的特征值,计算该段特征值的平均数,得到原始特征值与平均数之比,即相对特征指标。对相对特征指标进行7点滑移平均处理
(1)
其中:xRRX为原始特征与平均数的比值;xMA为最终相对特征指标。
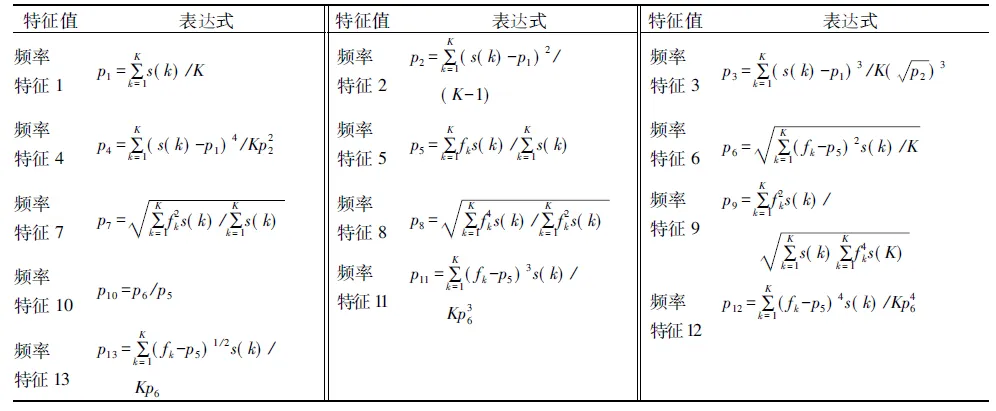
表1 频域指标
1.3 基于PCA的滚动轴承衰退性能指标的建立
PCA实质是揭示多维数据之间的内在关系,通过一种空间变换方式,实现高维数据能够用少数主成分来描述[9]。其算法流程如图2所示。
时域和频域特征指标经标准化和滑移处理后的相对特征指标组成的矩阵表示为
X=(X1,X2,…,Xι,…,Xp)T
(2)
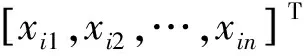
对原始矩阵进行零均值处理,通过式(3)的线性变换得到新的坐标系Y1,Y2,…,Yp,将X的协方差矩阵的特征值λ由大到小排列,通过线性组合得到第1,第2,…,第p个主成分。将第1主成分作为衰退性能指标,用于滚动轴承的寿命预测
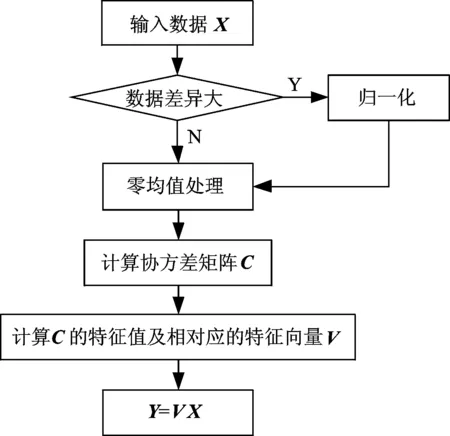
图2 PCA分析算法流程Fig.2 Algorithm flow of PCA analysis
(3)
2 滚动轴承寿命预测
利用滚动轴承退化过程的相似性,对当前需要预测的退化过程与历史退化过程进行相似性匹配,实现对未知过程的预测。
2.1 相空间重构技术简介
相空间重构理论指出:一个n维系统有n个状态变量,这n个状态变量可以构成一个n维空间,这个空间称为相空间。对非线性时间序列的建模和预测一般都可以在相空间中进行,在相空间重构中嵌入维数和时间延迟是影响相空间重构的重要参数。
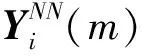
计算以下3个变量
当E1(m)在某个特定值m0后不再发生变化或者变化很小,此时的即为时间序列相空间重构的最小嵌入维数。
2) 时间延迟的选取。时间延迟τ对时间序列进行相空间重构有着重要的影响,若τ过大,则相空间中的矢量变得随机,重构后的矢量丢失大部分原动力系统信息;若τ太小,重构矢量之间相关性太强,无法很好地体现系统的演化规律。
如果S为原始数据序列{x(t)}(t=1,2,…,n),Q为S的时间延迟数据序列{x(t+τ)},则由Q和S可得到一个二维重构图,互信息熵的计算公式为
(9)
其中:si和qi为二维重构图中的点;Psq(si,qj)为当S=si,Q=qj时,重构图中联合分布概率;Ps(si),Pq(qj)为边缘分布概率,采用网格法对其进行计算。
当互信息熵I第1次达到极小值点时,此时的τ即为所求最佳时间延迟。
2.2 退化过程的对比
通过历史退化过程的衰退性能指标序列建立历史退化模型,以该模型为基准与当前退化过程进行对比,如图3所示。
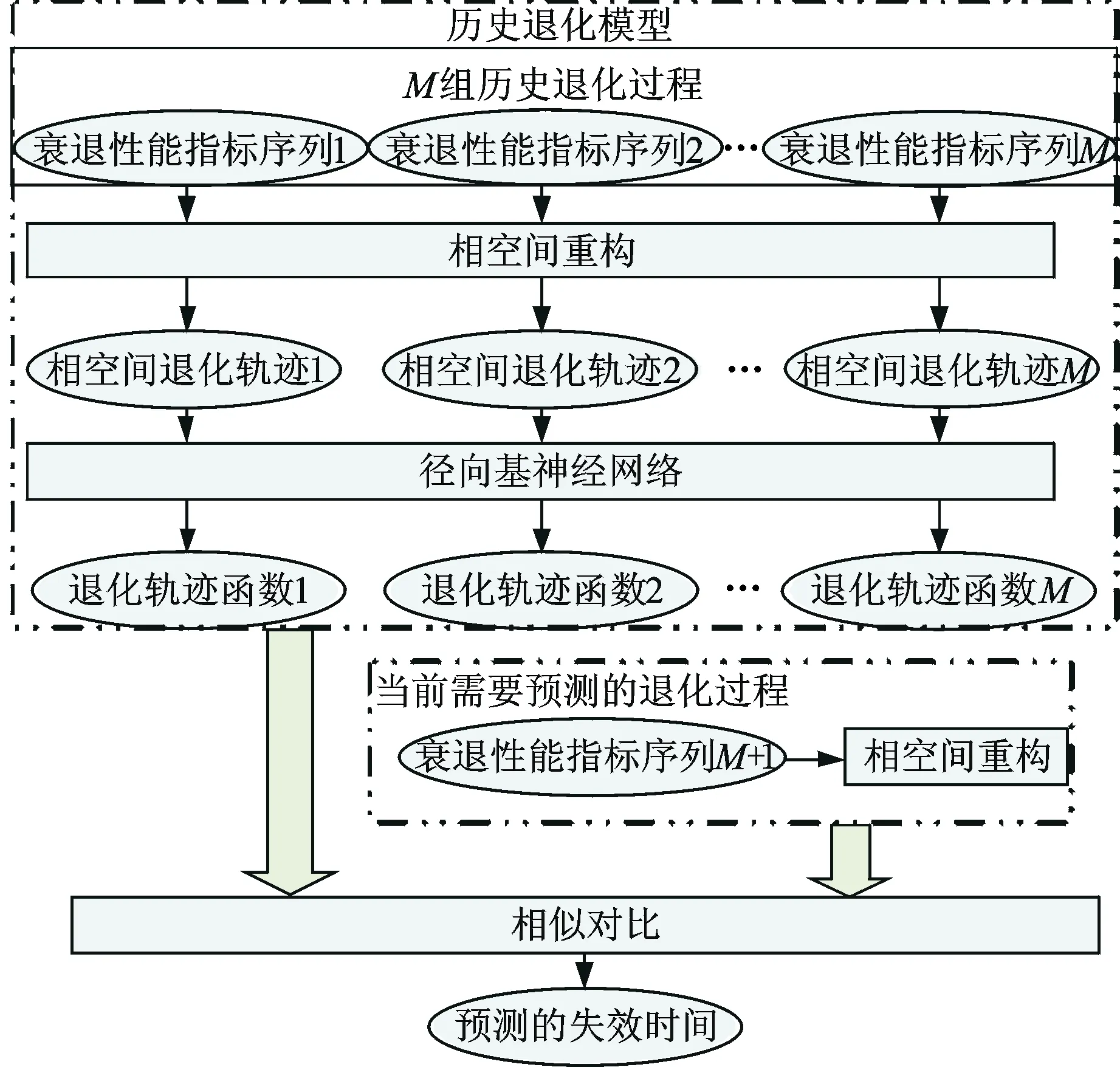
图3 当前退化过程与历史退化过程的对比Fig.3 Comparison between the current degradation process and the historical degradation process
1) 历史退化过程在相空间中展开。对M组历史退化过程的衰退性能指标序列进行相空间重构,实现滚动轴承退化过程的动力学轨道在相空间中完全展开。
2) 相空间中退化轨迹函数的学习。利用径向基(radial basis function,简称RBF)神经网络对非线性函数优良的逼近能力获得非线性轨迹函数。假设第i组(长度为n)历史退化过程的衰退性能指标序列经过相空间重构后矢量为
xxik(t)={xi(tk),xi(tk+τi),…,
xi(tk+(mi-1)τi)}
(10)
其中:k=1,2,…,L;L=n-(mi-1)τi。
将重构后的矢量{xxik(t)|k=1,2,…,L}和对应的服役时间{tk|k=1,2,…,L}分别作为输入和输出进行RBF神经网络的训练,得到第i组历史退化过程的相空间轨迹函数。
3) 预测失效时间。假设当前需要预测的退化过程为第M+1次退化过程,对应的运行时间为TM+1,对衰退性能时间序列{xM+1(t1),xM+1(t2),…,xM+1(tn)}进行相空间重构,将重构矢量输入到训练完的RBF神经网络中进行学习,获得1组估计的运行时间向量[T1,T2,…,TM],计算该运行时间与实际运行时间偏差
ei=(Ti-TM+1)2(i=1,2,…,M)
(11)
在时刻TM+1处可以得到一个误差向量e=[e1,e2,…,eM],从而得到该时刻退化轨迹与历史退化轨迹的相似程度
(12)
根据相似程度和历史服役寿命可预测滚动轴承在当前时刻的失效时间
(13)
其中:tM+1为当前时刻预测的失效时间;ti为滚动轴承历史服役寿命。
在下一次预测时,通过伸缩窗扩大性能指标数据,重复以上的步骤得到一个新误差向量,将其与上次计算的误差向量相加重新赋值给新误差向量。
2.3 平均寿命的估计
为了提高预测的准确性,将历史失效时间和当前预测的失效时间进行匹配作为样本,采用RBF神经网络的方法扩充样本建立概率模型,实现平均寿命的计算,如图4所示。

图4 失效时间的动态概率模型Fig.4 Dynamic probabilistic model of failure time
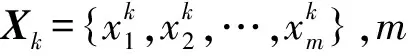
(14)
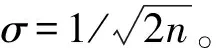
用t代替式(22)中的y,得到平均寿命
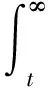
(15)
在下一次观测时,将上次计算的平均寿命加入到历史失效时间库中,通过历史样本的不断积累使分析样本不断扩大,估计不同观测时刻的平均寿命。
3 试验验证
3.1 数据来源及说明
笔者采用“IEEE PHM 2012 Prognostic challenge”提供的滚动轴承寿命数据进行验证。试验装置如图5所示,滚动轴承具体参数见表2。在转速为1.8kr/min、载荷为4kN的情况下采集7组滚动轴承退化失效过程的振动数据,采样周期为10s,采样频率为25Hz,采样时长0.1s。其中6组作为训练,1组作为当前分析对象进行跟踪和预测,该跟踪轴承的时间长度为238min。

图5 滚动轴承寿命实验装置Fig.5 Life test device of rolling bearings
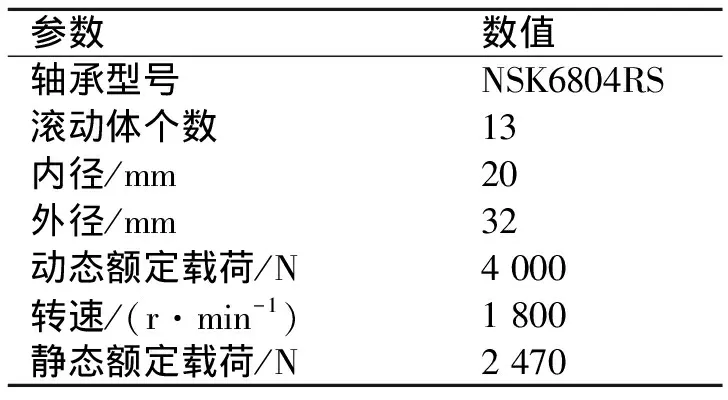
NSK6804RS13/mm20/mm32/N4 000/(r·min-1)1 800/N2 470
3.2 衰退性能指标的建立
通过前文方法建立一个有效的衰退性能指标序列。7组滚动轴承的特征指标共7×27个。图6中的均值、图7中的偏斜度指标、图8中的p3和p4特征指标稳定性较差;图7中的峰值指标和裕度指标虽然在滚动轴承退化过程中呈现了一定趋势,但是总体上信息较嘈杂。因此剔除这些指标,将剩下指标进行PCA融合得到衰退性能指标,如图9所示。

图6 滚动轴承的有量纲时域指标Fig.6 Dimensional time domain index of rolling bearings
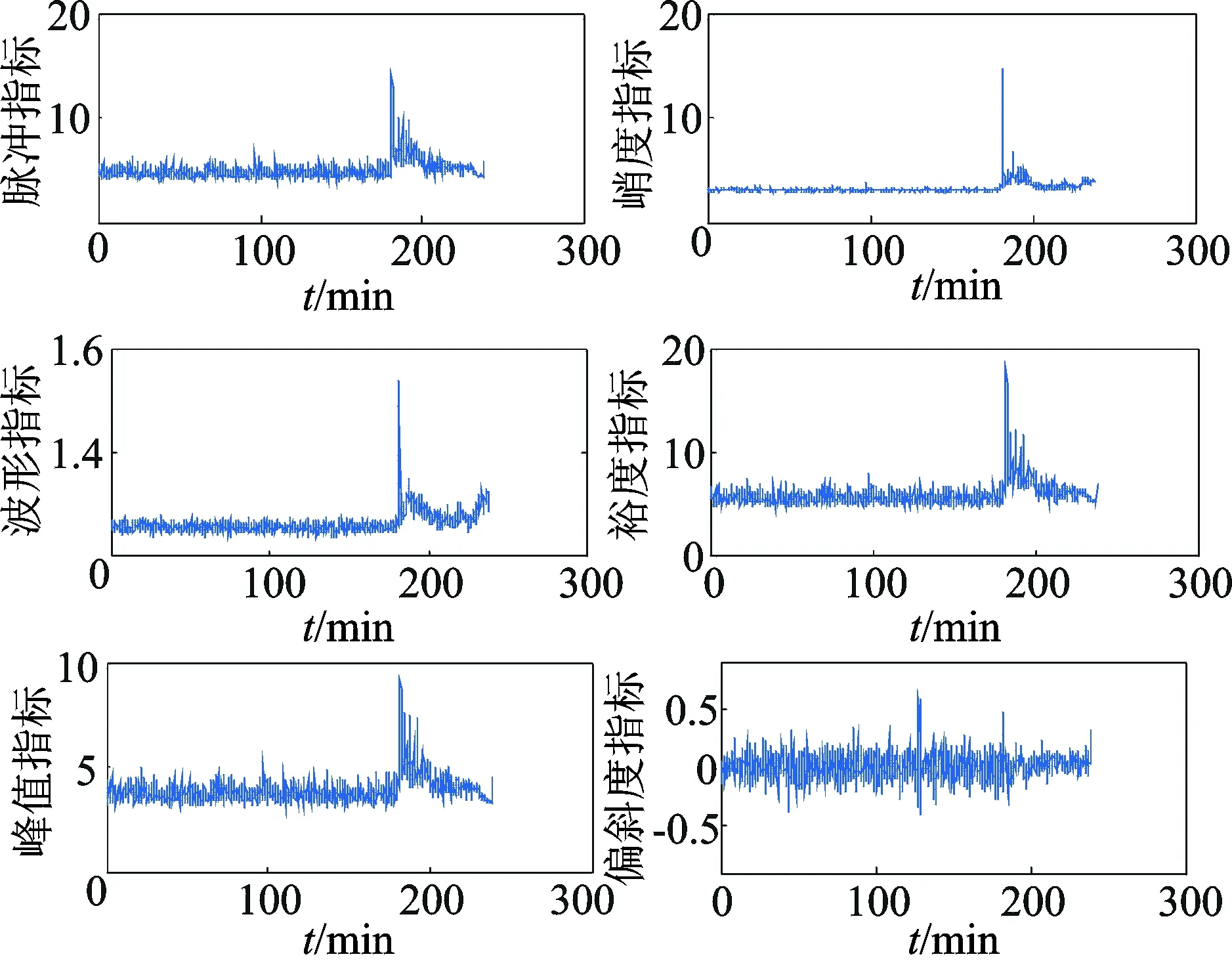
图7 滚动轴承的无量纲时域指标Fig.7 Dimensionless time domain index for rolling bearings

图8 滚动轴承的频域指标Fig.8 Frequency domain index of rolling bearings
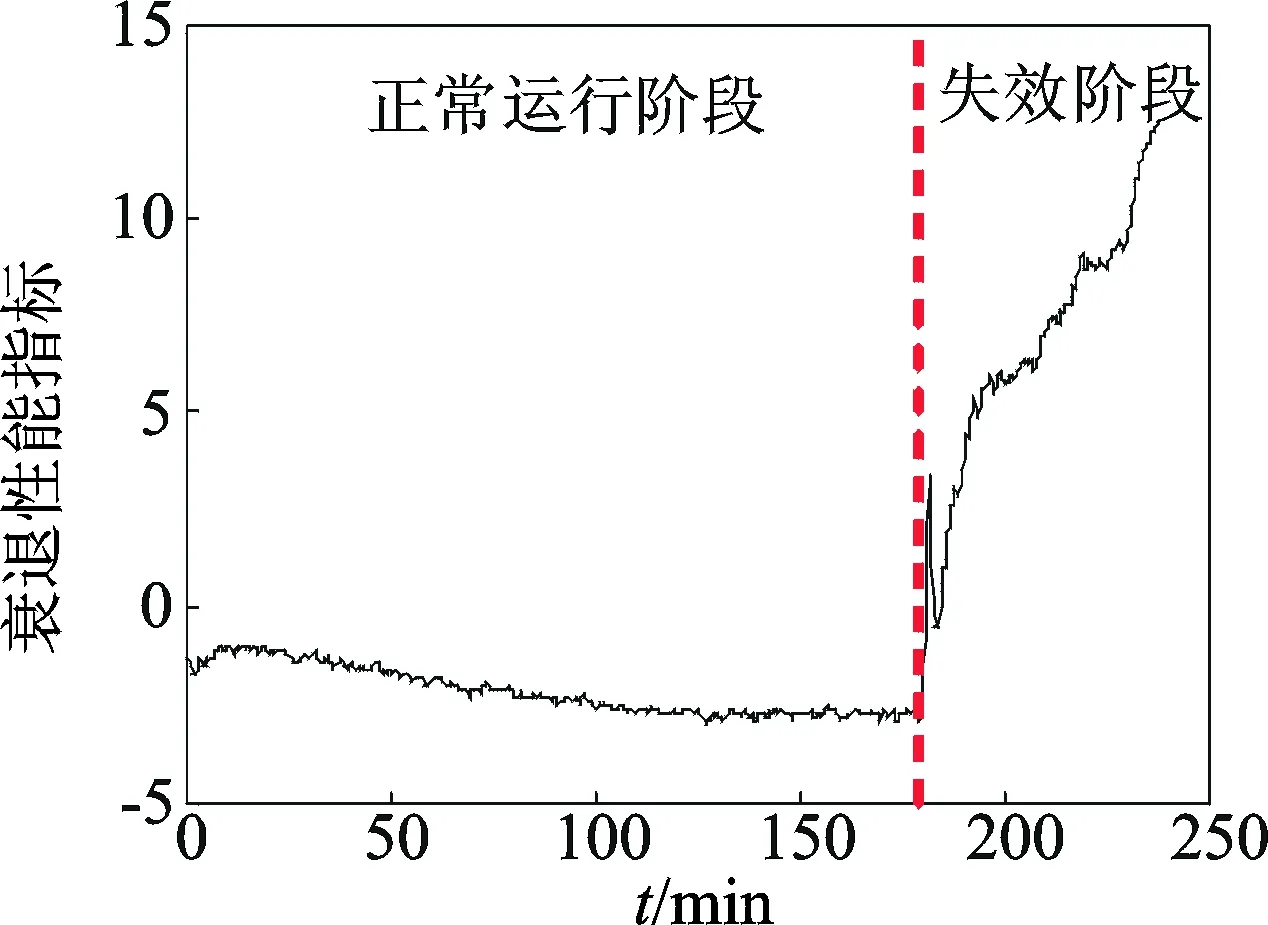
图9 滚动轴承的衰退性能指标Fig.9 Fading performance index of rolling bearings
图9表示通过PCA融合的衰退性能指标,可以看到融合后的衰退性能指标的退化趋势更加明显。图中性能指标在180min存在一个明显的波动拐点,一般将这个点对应的时间称为首次预测时间(first predicting time,简称FPT),并以此将轴承运行阶段分为正常运行阶段和失效阶段[7]。在第1阶段,轴承运行平稳,一旦故障发生,轴承进入第2阶段。可以看到进入第2阶段后衰退性能指标有一个先上升后下降的过程,这是因为当表面缺陷刚刚形成时,连续滚动会造成小的剥落或者裂纹,但是随后会被连续滚动接触抚平,当损伤扩展到更广的区域时,振动水平再次上升[11]。这种现象被称为“愈合”现象[12]。图10中6组训练轴承的衰退性能指标在进入失效阶段后,都会有一定程度的波动,以轴承3最为明显,说明轴承3在进入失效阶段后,存在较为明显的连续剥落或者裂纹损伤。
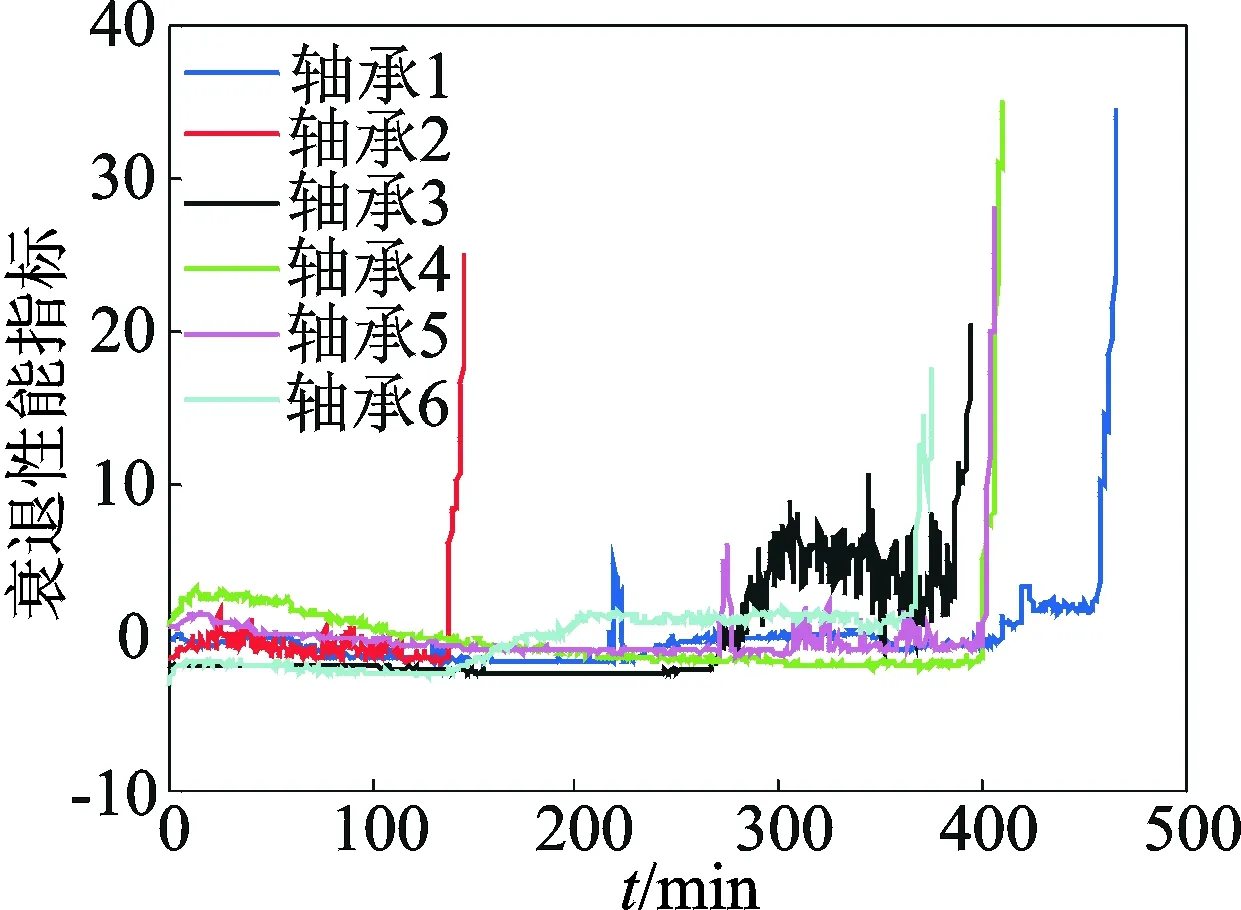
图10 6组训练滚动轴承的衰退性能指标Fig.10 Fading performance indexes of 6 groups of training rolling bearings
3.3 相空间重构参数的确定
利用Cao方法确定6组训练滚动轴承衰退性能指标序列的嵌入维数m,如图11所示。在应用中认为当E1变化很小时,对应的嵌入维数即为最小嵌入维数。利用互信息法确定这6组序列的时间延迟τ如图12所示,当互信息熵I第1次达到极小值点时,相对应的时间延迟τ即是该序列相空间重构的最佳时间延迟τ。通过图11和图12看出,每组的嵌入维数和时间延迟相差不大。选取时间延迟的均值τ=15和6组中最大的嵌入维数m=10作为相空间重构的参数。
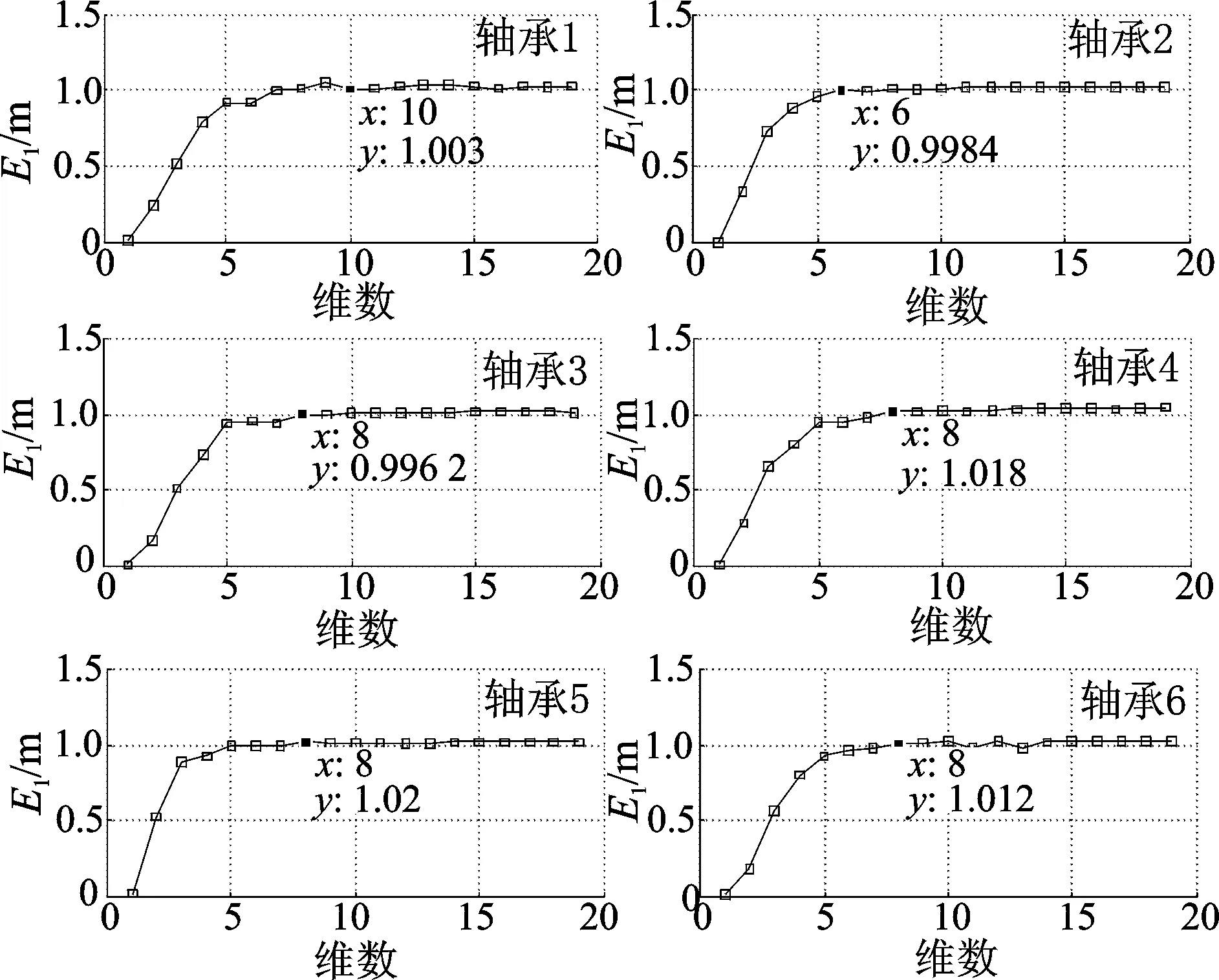
图11 6组滚动轴承衰退性能指标序列的嵌入维数Fig.11 The embedding dimension of 6 sets of rolling bearing fading performance index sequence

图12 6组滚动轴承衰退性能指标序列的时间延迟Fig.12 The time delay of 6 sets of rolling bearing fading performance index sequence
3.4 平均寿命的计算
为了验证本研究通过多特征融合的衰退性能指标预测的寿命比单一特征指标(峭度指标)预测的寿命更加接近真实寿命,将两组预测结果进行对比,如图13所示。T为预测的平均寿命,T′为实际服役寿命,T′=238min。整体寿命误差率为
(16)

图13 滚动轴承平均寿命误差对比图Fig.13 Comparison of average life error of rolling bearings
由图13可知,通过多个特征融合的衰退性能指标较单一特征指标预测的误差更小,说明其更接近滚动轴承的真实寿命,同时随着滚动轴承运行时间的增加,平均寿命越来越接近真实寿命。针对“IEEE PHM 2012 Prognostic challenge”,也有学者对此进行了算法研究,Wang[13]采用了基于轴承频率特征的包络分析。Sutrisno等[14]采用了3种方法,效果最好的是采用振动频率特征异常检测计算生存时间比。以运行到189min为例,相比本研究中的方法,这两组方法得到的结果误差分别为20.2%和19.8%,均大于图13中的误差。
4 结束语
本研究通过对滚动轴承在其寿命时间轴上间断地性能指标的累积,实现在线服役滚动轴承寿命的动态预测。通过PCA技术对滚动轴承振动信号时域和频域的多个特征进行融合,建立了一个衰退性能指标序列。利用相空间重构技术和RBF神经网络对历史滚动轴承衰退性能指标序列进行相空间重构,获得了历史衰退性能指标序列的相空间轨迹函数。通过与当前退化过程进行相似对比,得到了一个预测的失效时间,最终利用这个预测的失效时间和历史失效时间进行匹配组合作为统计样本,建立了基于失效时间的概率模型,实现了平均寿命的估计。试验结果表明,通过多个特征融合的衰退性能指标较单一特征指标预测的误差更小,说明其更接近滚动轴承的真实寿命,验证了方法的有效性。

