双连杆柔性机械臂振动主动控制与实验*
邱志成, 李 城
(华南理工大学机械与汽车工程学院 广州,510641)
引 言
相对于刚性机械臂,柔性机械臂具有惯性小、能耗低和运动速度高等优点[1],但由于其质量较轻,刚度低和模态阻尼小,使得柔性机械臂在转动或受到外部扰动时,会产生较长时间的自由振动,对其稳定性和工作精度产生较大影响,所示对柔性机械臂的振动控制显得尤为必要[2]。
柔性机械臂作为一种强耦合非线性时变多输入多输出(multiple input multiple output,简称MIMO)分布参数系统,其复杂性不仅体现在动力学建模分析方面,更主要表现在控制器的设计上。Book等[3]对柔性机器人的振动问题进行了研究,柔性机械臂的振动控制方法主要分为前馈和反馈控制。由Singhose 等[4]定义的输入整形技术作为一种前馈控制策略,考虑系统的物理和振动特性来降低系统的相应模态振动,将输入信号进行整形,在抑制柔性结构体振动研究方面取得了突破性的成果,且在实际中能得到有效应用。针对柔性机器人机构的振动问题,楚中毅等[5]提出采用脉冲整形技术减小末端残余振动,并结合压电陶瓷作为从驱动源采用闭环反馈控制策略抑制末端残余振动,实现了二自由度平面并联压电智能杆机构高速高精度的点位控制。胡庆雷等[6]提出滑模控制与输入整形技术结合的混合控制方法来抑制航天器姿态调整时发生的振动。陈俊恒等[7]采用输入整形算法对固晶机生产过程中存在的振动进行抑制,取得了良好的效果。近年来,输入整形技术在柔性机构的减振控制领域广泛应用,取得了良好的抑振效果。这种控制方法无需传感器,确定输入后不再考虑系统参数变化。
反馈控制主要采用应变片、加速度计或压电陶瓷片[8]等作为传感器测量柔性臂振动信号,作为反馈信号结合不同控制算法对其振动进行抑制,PID控制[9]、模糊控制[10]、自适应控制[11]及神经网络[12]等控制方法在柔性机械臂振动控制中得到广泛引用。Yurkovich等[13]对柔性机械臂在负载未知的条件下,采用变增益自适应方法控制其末端位置,对柔性臂振动控制有一定的效果。Zhang等[14]提出对两自由度柔性臂进行偏微分建模,以避免由于模态截断可能产生的观测和控制“溢出”问题,并采用自适应边界技术设计控制器,仿真结果表明能有效抑制柔性臂的振动。Pradhan等[15]使用非线性自适应模型预测控制对柔性臂进行变负载末端位置控制,在系统辨识中采用了自动回归滑动平均模型(auto regressive moving average model,简称ARMAX)模型,通过与直接自适应和自校正控制方法的对比,表明该方法对柔性臂在变负载时的末端轨迹跟踪和抑振能力较强,但非线性模型辨识极大增加了计算量,导致对系统硬件性能的要求增加。Sadaki等[16]采用自校正控制对柔性臂末端轨迹跟踪和抑振控制时,也采用ARMAX模型对两自由度柔性臂进行了系统辨识,并结合人工神经网络(artificial neural network,简称ANN)算法学习比例积分(proportion integration,简称PI)控制器的参数,仿真结果表明其对机械臂的振动抑制有效。自校正算法作为自适应算法的另一大类,应用在柔性臂的振动抑制中的研究并不广泛,由于系统非线性等因素存在,系统辨识模型精确度与复杂度的问题也值得进一步探讨。
针对柔性机械臂的振动主动控制问题,设计了三自由度刚柔耦合机械臂实验平台,采用伺服电机作为驱动器,粘贴在柔性悬臂梁根部表面的压电片作为传感器。测量的振动信号经滤波后,进行模态辨识,采用不同方法进行柔性臂振动主动控制的实验比较研究。采用基于输入整形的前馈控制和广义最小方差自校正的反馈控制策略,进行了柔性臂在给定运动轨迹和设定位置两种情况下的实验,验证所研究的方法对抑制柔性臂振动抑制的有效性。
1 控制器设计
1.1 自校正控制算法
自校正控制作为一种自适应控制算法,主要根据系统的实际输出、期望输出、外部扰动和控制量等可测量来实时改变系统的控制参数,实现最优控制使系统工作在期望位置。将自校正控制策略引入刚柔耦合机械臂的振动控制中,采用递推增广最小二乘法实时辨识被控对象模型参数,并根据参数估计设计最小方差控制律,其基本结构如图1所示。

图1 基于GMVSTC柔性臂振动控制框图Fig.1 The block diagram of GMVSTC based vibration control for the flexible manipulator
1.1.1 单步输出预测模型
设被控对象为受控的自回归滑动平均差分方程(controlled auto regressive moving average,简称CARMA)模型[17]
A(z-1)y(k)=z-dB(z-1)+C(z-1)ξ(k)
(1)
其中:y(k)和u(k)为系统输出和输入;ξ(k)为方差为σ2的白噪声;d为对象纯延时;A(z-1),B(z-1)和C(z-1)为被控对象和扰动对象的加权多项式。
(2)
其中:b0≠0。
对象基于k时刻和k时刻之前的输入输出数据记为
{Yk,Uk}={y(k),y(k-1),…,u(k),u(k-1),…}
(3)
基于{Yk,Uk}对k+d时刻的输出的预测为
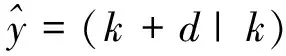
(4)
输出预测误差为

(5)

C(z-1)y*(k+d|k)=G(z-1)y(k)+F(z-1)u(k)
(6)
其中
且E(z-1),G(z-1)和F(z-1)分别满足
(9)
其中:ne=d-1;ng=na-1;nf=nb+d-1。
1.1.2 广义最小方差控制律
与最小方差控制不同,广义最小方差控制算法(GMVSTC)在求解控制率的性能指标中加入对控制量的加权项,达到抑制控制作用剧烈波动的目的,只要选择合理的加权多项式就可使其适用于非最小相位系统。选择控制器性能指标函数为
(10)
其中:y(k+d)和yr(k+d)为系统在k+d时刻的实际输出和期望输出;u(k)为第k时刻的控制量;P(z-1),R(z-1)和Q(z-1)对应为实际输出、期望输出和控制量的加权多项式,分别起到改善闭环系统性能、柔滑期望输出和约束控制量的作用。
控制器参数递推估计公式为
(11)
其中
(12)
使性能指标最小的广义最小方差控制率[17]为
u(k)=
(13)
由于被控对象的参数未知,采用直接自校正控制,利用递推算法直接估计广义最小方差的参数,同时可避免求解Diophantine方程,上述控制律表达式为
(14)

GMVSTC算法的具体实施流程如下:
2) 采样当前的实际输出y(k)及期望输出y(k+d);
4) 由式(14)计算实施控制量u(k);
5) 返回步骤2,并令k=k+1,继续循环步骤2~4。
由于控制指标式(10)中具有对控制量的限制,故可以避免控制量过大时,使数模转换装置或执行器处于饱和状态影响控制品质。同时,闭环系统特征方程为
(15)
可以看出,选取合适的q0控制率对于B(z-1)中存在稳定零点的非最小相位系统可以实现稳定的控制。
1.2 输入整形器设计
输入整形是计算机控制中为减小系统残余振动的一种前馈开环控制方法,由一系列脉冲序列组成的输入整形器与参考输入命令卷积后生成一个被整形的输入量来驱动系统。图2为指令整形器结构[18]。

图2 指令整形器的结构Fig.2 The structure block of the input command shaper
Xu等[19]在研究柔性机械臂的动力学特性时指出第1阶模态起决定作用,在保证精度的情况下,取较少的模态阶数可简化控制器的设计。大多数系统的数学模型为高阶系统,为对其进行深入研究,可忽略非主要因素,将系统简化为二阶系统,表达式为
(16)
对于式(16)给出的振动系统,在最后一个脉冲作用时刻tN后,系统单模态脉冲响应残余振动幅值表达式为
(17)
其中
(18)
(19)
其中:Ai和ti为第i个脉冲的作用幅值和时刻。

(20)

为减小模型不精确带来的影响,增加输入整形器对系统振动的鲁棒性能,可添加约束
(21)
(22)
由此可解得一个含3个脉冲序列的零振荡导数(zero vibration and derivative,简称ZVD)输入整形器
(23)

因此,经过整形后的系统输出时域表达式[7]为
(24)
柔性臂开环输入整形系统如图3所示。

图3 开环输入整形系统Fig.3 The open loop input shaping system
推广到多个模态可以独立设计对应每个模态的脉冲序列,共同驱动系统,使系统在执行终点tN后的残余振动为零。
输入整形对柔性系统中的振动有较好的抑振效果,但其对模型参数精度要求较高,导致鲁棒性差。增加脉冲个数可以提高鲁棒性,但会增加引入的时滞。ZV整形器不敏感度为0.06,即0.97~1.03ωmodel内的振幅小于整形振幅的5%。ZVD整形器不敏感度为0.29[20]。在实验中采用实验法建模,则能较为精确地得到柔性臂的振动模态,结合模态分析得到系统振幅较大的模态频率,可保证指令输入整形算法有较好的稳定性。
2 实 验
2.1 实验系统描述
针对柔性机械臂运动中的振动控制问题,设计了如图4所示的柔性机械臂实验平台,该平台结合压电智能材料作传感器、交流伺服电机作驱动器组成刚柔耦合系统,对前述控制方法进行实验研究并比较实验结果。
两额电机输出轴均经过减速比1∶64的减速器后连接到两机械臂上。柔性臂为环氧树脂材料薄板,密度为1 840 kg/m3,其长度L1=1 000 mm,宽度b1=50 mm,厚度h1=2 mm; 刚性臂由铝板制成,密度为2 700 kg/m3,其长度L2=300 mm,宽度b2=80 mm,厚度h2=10 mm;压电传感器尺寸为50 mm×15 mm×1 mm,压电应变常量和弹性模量分别为-166×10-12m/V和63 GPa。
本实验利用压电片作为传感器,驱动器为三菱交流伺服电机。刚性臂的驱动电机为电机Ⅱ,功率为400 W;柔性臂的驱动电机为电机Ⅰ,功率为100 W。控制卡为美国GALIL公司生产的Galil-DMC-1846型四轴运动控制器,电机控制方式为速度控制模式。柔性梁的变形所产生的振动型号经压电片测得,信号由放大器(型号为YE5850)放大到幅值为(10~+10V之间的电压信号后,经GALIL控制卡16位AD转换模块转换为数字信号输入计算机,作为反馈信号。经过滤波后结合控制算法加算得出控制电压,经控制卡的DAC模块转换后输出振动控制模拟信号,经由伺服驱动器对电机进行控制,以实现机械臂按规划速度运行的同时对柔性臂的振动进行抑制。

图4 实验装置照片Fig.4 The photograph of the experimental setup
2.2 实验结果及分析
在保持两电机轴位置固定时通过外部激励使柔性臂产生振动,振动信号经分析后可得到柔性臂的模态频率。激励柔性臂产生自由弯曲模态振动,振动信号如图5所示。由于减速器输入轴和输出轴之间存在间隙,柔性臂并不是端部完全固定的悬臂梁,外界激励引起柔性臂的振动在间隙两侧克服摩擦来回做功,能量耗散较快,所以与绝对的悬臂梁相比,柔性臂的自由振动衰减得略快,在5s多一点就衰减到小幅值的振动。但作为对比实验,每次实验都是在同一实验台上且在相同条件下进行的,故实验结果仍不失一般性,所提出的控制策略对电机输出轴不经过减速器直接驱动柔性臂或减速器无间隙的情况仍有效。自由振动信号经过快速傅里叶变换可得频率响应曲线如图6所示, 由图可知,测得的前2阶弯曲振动模态频率为f1=3.02 Hz,f2=8.72 Hz,则前2阶弯曲振动角频率分别为ω1=2πf1=18.84 rad/s,ω2=2πf2=54.76 rad/s。1阶模态阻尼比为
(25)
其中:At1和At2分别为t1和t2时刻的振动幅值,通常选为两个峰值处。
由图5和式(25)可计算出1阶模态阻尼比ξ1=0.009 7。
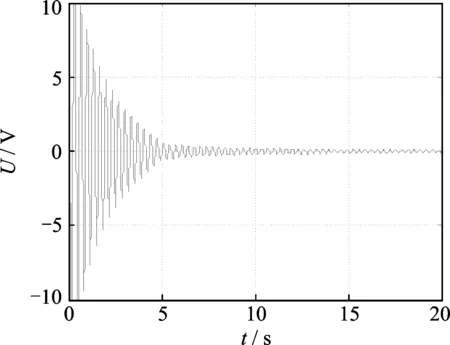
图5 柔性臂自由振动信号Fig.5 The free vibration signal of the flexible manipulator

图6 模态频率响应曲线Fig.6 The frequency response curve of the free vibration bending modes
电机转动采用角位移和角速度反馈的PD控制,控制率为
(26)

总的控制量可表示为
τ=τ0+u
(27)
其中:u为使用不同控制算法计算得到的柔性臂振动控制量。
实验先将刚性臂固定,给定柔性臂的期望运动速度为T型轨迹,电机转动角速度ω=220.8 r/min,运行时间为6 s。如图7所示,由于电机驱动力矩的扰动和系统惯性,柔性臂产生了较长时间的大幅值振动。
对振动采用PD控制,控制率为
(28)
其中:e(t)=yr(t)-y(t);yr(t)=0为柔性臂的期望变形量;y(t)为压电片检测得到的实际变形量;控制参数kp1=0.02,kd1=0.003。
图8为采用PD控制的试验结果曲线,和图7相比,振动被有效抑制。

图7 柔性臂转动时未进行主动振动控制实验曲线Fig.7 Experimental curve for the flexible beam slewing without active vibration control

图8 柔性臂转动时同时采用PD主动振动控制Fig.8 Simultaneous slewing and vibration PD control for flexible manipulator
对振动采用GMVSTC,由频率辨识可看出对柔性臂的振动控制主要是抑制其前2阶振动模态,故控制率中取na=2,nb=1,nc=1。实验中驱动器和传感器为异位配置,且采样频率较大,可取纯延时d=4。为在不影响控制精度和稳定性的前提下简化运算,取P(z-1)=1,R(z-1)=1和Q(z-1)=q0,q0根据实际需求调节,过小会失去对控制作用的约束,不能保证控制稳定性,难以实现最优控制。由GMVSTC算法的具体实施流程可计算出控制量u2,进行实时控制。图9(a)和图9(b)分别为采用GMVSTC算法主动振动控制响应曲线和参数辨识调整曲线。图9和图8相比,振动被抑制的效果进一步增强,可知参数可以在线调整的GMVSTC算法优于PD控制算法的性能。

图9 柔性臂转动时采用GMVSTC主动振动控制Fig.9 Simultaneous slewing and vibration GMVSTC active control for flexible manipulator
将系统辨识得到的参数带入式(19)和式(22),可得到抑制柔性机械臂振动的ZV和ZVD输入整形器
(29)
将相同的T形速度规划信号经上述整形器后分别加载到系统,驱动柔性臂转动,如图10所示,表示两种速度加载命令和末端输出振动响应的波形对比。
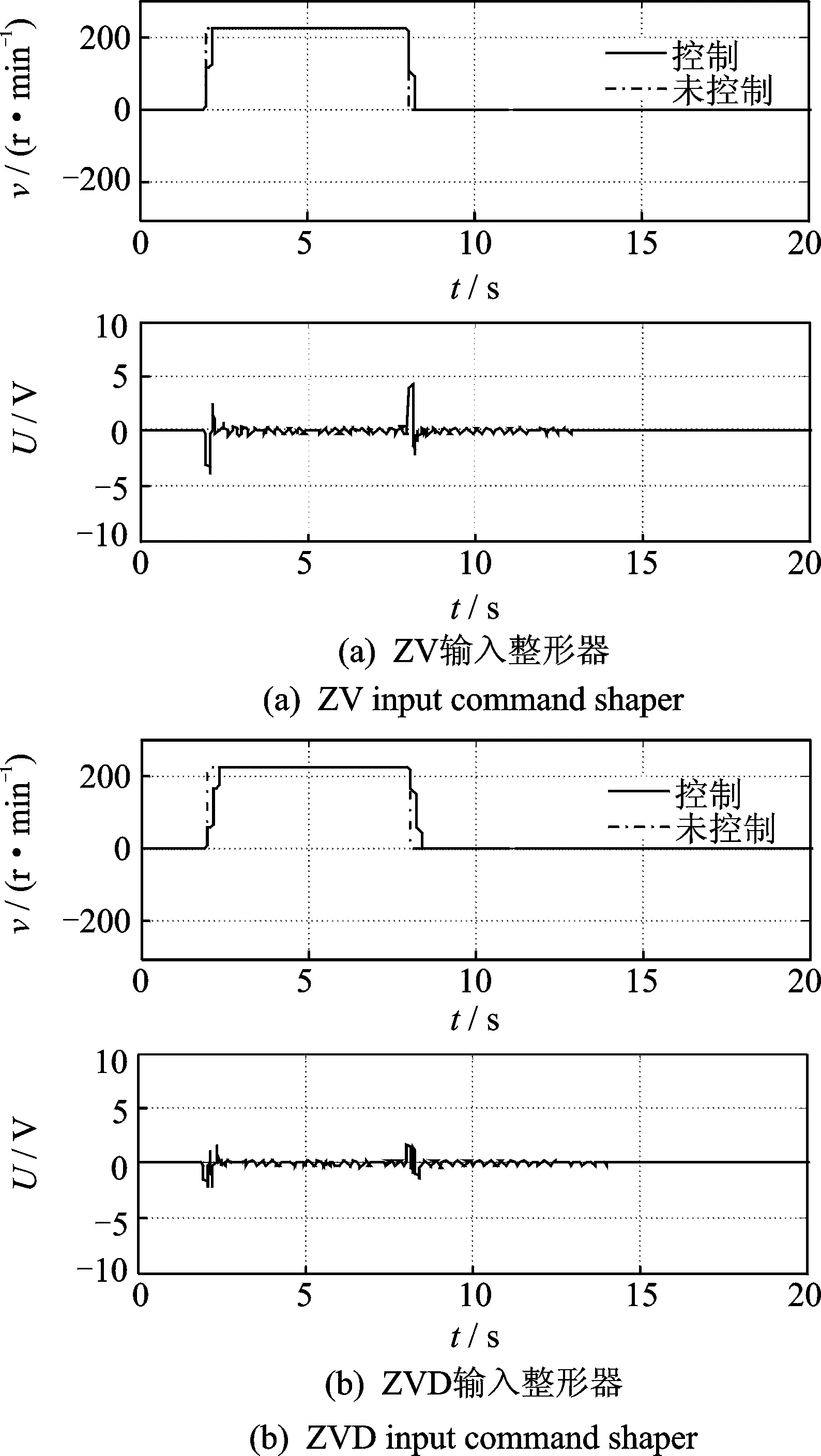
图10 整形器加载命令及其输出响应Fig.10 Input command shaper and output response
通过比较可以看出,对柔性臂由于电机驱动力矩产生的大幅值振动,各种抑振方法效果不尽相同。PD控制对柔性臂的残余振动有一定的控制效果,但对小幅值振动抑制能力不佳;采用基于CRAMA模型的广义最小方差自校正控制方法,能快速将大幅值的振动抑制,对小幅值的振动也有较好的效果;基于输入整形的前馈控制引入延时以避免激起柔性臂的大幅值振动。柔性臂的残余振动曲线是幅值衰减的正弦曲线,使用电机作为驱动源进行控制,由于存在驱动死区和减速器间隙等非线性因素,对柔性臂较小幅值振动的抑制不能很快达到理想的完全静止状态,故可在各种控制条件下,取柔性臂运动结束后的振动曲线幅值首次小于0.3V所需的时间作为性能指标进行对比,结果如表1所示。
柔性臂所规划的T形运动在第8 s时结束。通过表1可以看出:若不对残余振动进行抑制,柔性臂运动结束后的残余振动将持续到17.65 s;对残余振动进行PD控制,可明显缩短大幅值振动的时间,但由于其参数值固定,对小幅值振动抑制作用不佳,需到第10 s左右才能将振动幅值抑制到小于0.3 V,所需时间较长;而GMVSTC算法可在第9 s左右就能达到目标,所需时间减少了50%;基于输入整形的控制方法,能在运动结束0.5 s左右将振动幅值抑制到小于0.3 V。
表1 不同情况下振动幅值首次小于0.3 V所需时间
Tab.1 The required time for vibration amplitude less than 0.3 V for the first time in different cases

PDGMVSTCZVZVD/s17.6510.088.958.478.44
为了说明当柔性臂匀速运动时间段T变窄时上述两种控制方法也有较好的抑振效果,下面以柔性臂匀速运动时间缩短为0.5T为例,PD,IST和GMVSTC这3种算法对柔性臂抑振控制效果如图11~13所示。由4组控制效果图对比可知,缩短柔性臂运动时间后,IST和GMVSTC也能较好地实现柔性臂抑振控制,从而可以看出所提出方法对不同的工况有良好的实用性。

图11 柔性臂匀速运动时间减半PD振动控制Fig.11 Flexible beam slewing under PD vibration control scheme when the time for uniform motion time is halved

图12 柔性臂匀速运动时间减半整形器加载命令及其输出响应Fig.12 Input command shaper and output response when flexible link uniform motion time is halved
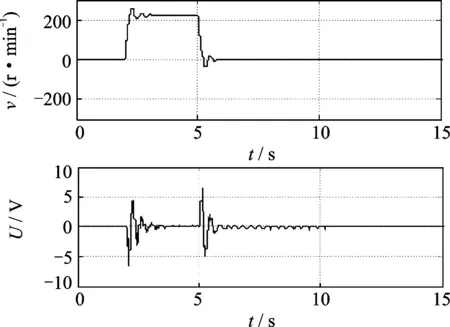
图13 柔性臂匀速运动时间减半STC振动控制Fig.13 Flexible beam slewing under STC vibration control scheme when the time for uniform motion time is halved
其中基于输入整形的开环控制技术设计过程简单,快速抑振效果好,不需要振动检测等复杂装置;而基于GMVSTC的振动控制方法虽然需要加装振动检测装置,但在对柔性臂变负载或位置固定时由于外部扰动引起的振动有很好的抑振效果。
设置柔性臂期望转角为零,即电机Ⅰ位置固定,在刚性臂电机端输入T形速度规划,转速和转动时间和前述T形速度规划相同,柔性臂上压电片测得的振动信号曲线如图14所示。
分别结合PD控制和广义最小方差自校正控制,同样用柔性臂的驱动电机,即电机Ⅰ为振动控制的驱动源,采用对柔性臂进行振动主动控制,这里PD的控制参数仍选取kp1=0.02,kd1=0.003,实验结果如图15和图16所示。

图14 柔性臂固定时自由振动曲线Fig.14 Free vibration curve when flexible arm is fixed

图15 柔性臂固定时采用PD主动振动控制Fig.15 Vibration control under PD controller when flexible arm is fixed

图16 柔性臂固定时采用GMVSTC主动振动控制Fig.16 GMVSTC active vibration control scheme when the flexible arm is fixed
第2 s之前,由于实验环境非绝对理想环境,柔性臂在外界GMVSTC辨识的参数出现波动。刚性臂在第2 s开始运动,外界激励使参数出现剧烈变化,振动控制开始加入。参数实时辨识使其快速调整到稳定值,第8 s时刚性臂运动停止,再次使辨识的参数出现波动,并再次快速调整到稳定值,对运动结束后的残余振动进行控制。
由图14、图15和图16比较可知:对于柔性臂关节电机Ⅰ锁定时,刚性臂的运动使柔性臂产生扰动,电机Ⅰ无运动指令输入,无法用输入整形器对柔性臂进行振动控制;PD控制由于控制参数固定,对小幅值的残余振动抑制效果不佳,振动持续时间没有明显变短,而且对不同的负载和柔性臂参数,需要对PD控制参数进行反复调整以到达最佳控制效果;相同情况下,采用GMVSTC控制算法对小幅值振动也能进行快速抑制,可明显减小振动持续时间,且能很好地应对变参数、变负载的情况,充分体现了自适应控制的优点。
3 结束语
笔者在对柔性机械臂进行模态辨识的基础上,对柔性臂在电机驱动力矩下产生的振动,分别设计了基于输入整形的前馈开环控制器和基于广义最小方差自校正控制的闭环控制器。在建立的刚柔耦合柔性机械臂实验平台上,采用这两种控制策略进行了振动主动控制,并用常规的PD算法进行了对比实验。通过实验结果的比较,柔性臂的振动明显被快速抑制,验证了所采用方法的有效性。通过对比实验,对两种控制方法的优缺点和各自适用条件进行了说明。

