高速磁悬浮鼓风机系统模型改进与实验*
杜 毅, 宋欣达, 韩邦成
(1.北京航空航天大学惯性重点技术实验室 北京,100191) (2.新型惯性仪表与导航系统技术国防重点学科实验室 北京,100191) (3.北京市高速磁悬浮电机技术及应用工程技术研究中心 北京,100191)
引 言
磁悬浮离心式鼓风机具有转速高、功率大、调速范围广等优点,在污水处理、高炉鼓风等领域已取得广泛应用[1-2]。在大部分的应用场合,对风机静态特性都有相应要求。文献[3]中,在控制炼铁所需高炉风压时,通过使用调节阀实现出口风压调节,但该方法会增大管道阻力,损耗能量,降低风机工作效率。文献[4]在控制隧道通风系统时,使用变频调速的方法,但并未涉及到风机与管道模型研究,未能得到管道出口压力与电机转速间精准的数学关系,调速范围具有随机性。文献[5]提出了使用流量和输出压力作为反馈的控制方法,只是其控制对象是针对永磁电机的磁悬浮轴承间隙,控制范围有限。传统Greitzer模型未考虑实际应用中由于地形限制而不可避免的弯形管道,并且存在限制使用地形的容腔,所以文献[5]中所建立的模型并不适用。考虑风机管道沿程压力损失和局部压力损失,能够改进传统Greitzer风机模型,为风压闭环控制器的设计奠定基础。笔者通过实验得到了电机转速与鼓风机出口压力间的关系,并验证了模型的有效性和准确性。
1 系统数学模型
本研究对象为离心式鼓风机,其主要结构部件为叶轮、蜗壳和进出气管道。驱动电机是30 kW高速磁悬浮永磁式电机,三维模型图如图1所示。
鼓风机建模方面,最经典的动态模型是由Greitzer[6]提出的,包含了风机、管道和容腔。图1所示的实验对象相比图2(a)所示的Greitzer经典模型,并未包含对地形有要求的容腔,考虑了应用价值极高的弯行管道,故模型更具有应用普适性。

图2 改进模型与原模型对比图Fig.2 Comparison between improved model and original model
笔者在经典风机系统模型基础上,针对包含弯管但不包含容腔的风机管道,建立了一个仅以电机转速作为控制量的数学模型,在建模时默认阀门保持不变。
1.1 鼓风机升压阶段数学模型
对于图2(b)中阶段Ⅰ,外部气体压力为p01,经过进气管道进入鼓风机后,鼓风机对其做功,压力升至p02,经扩压器输出至出口管道,有如下关系
p02=ψc(ω,m)p01
(1)
其中:ω为电机转速;m为气体质量流量;Ψc(ω,m)为鼓风机特性函数。
1.1.1 鼓风机特性函数模型
假定鼓风机在对气体做功过程中,与外界没有热交换,视其为等熵过程。对于理想气体,在等熵过程中,根据文献[7],有热力学关系
其中:cp为恒压条件下气体比热容;cv为恒容条件下气体比热容;κ=cp/cv,为绝热指数;T01为风机入口温度。
在气体流经鼓风机过程中,气体比焓增加来源于鼓风机对气体做功。考虑到该做功过程中的损耗,则可得以下关系
h02=h01+Δhideal-Δhloss
(4)
其中:h01为风机入口处气体比焓;h02为风机出口处气体比焓;Δhideal为风机传递给气流的理想比焓;Δhloss为风机对气流做功过程中所损失的比焓。
结合式(2~4),有
(5)
结合式(1,5),可以得到鼓风机特性函数为
(6)
根据文献[8],风机传递给气流理想比焓可由如下公式给出
(7)
1.1.2 鼓风机内气体损耗模型
气流经鼓风机从p01变化为p02的过程中,鼓风机对气流做功,会增加气流比焓。但在该过程中,总会发生能量损耗,主要来自以下几方面:a.气流流入叶轮和扩散器时的冲击损失Δhii和Δhdi;b.流经叶轮和扩压器时的表面摩擦损失Δhif和Δhdf;c.在叶轮处由于二次流导致的叶片负荷损失Δhbl。相比这3种损耗,其他损失可忽略不计,故本研究主要考虑这3种损失。
1) 冲击损失。冲击损失主要来源于气体流入叶轮和扩压器的过程中,为适应叶轮方向而改变流向导致的速度损失。气体在进入叶轮处的冲击损失示意图如图3所示。

图3 气流进入叶片时冲击损失Fig. 3 Incidence losses at the impeller
β1和V1分别为气流进入叶轮时的角度和对叶片的相对速度,β1b为叶片角度,V2为气流进入叶片后的相对速度,ΔV1即为气流的相对速度损失
(8)
由正弦定理可得
(9)
由图3可得
(10)
风机叶轮为径向式叶片结构,则α1=90°。对于管道内气体流速,有以下关系
v=m/ρ02A1
(11)
结合式(8~11)可得

(12)
其中:C1为气体绝对流入速度;U1为叶轮入口处切向速度;β1b为气流入口处叶片角度;ρ01为入口处气体持续进气密度;A1为进气通道面积。
根据文献[9],气体在扩压器处冲击损失和摩擦损失与叶轮处相似。如图4所示,气体相对速度为V2,沿角度β2进入扩压器,随即改变速度方向至β2b以适应扩压器,在该过程中,其切向速度ΔV2的动能被损耗掉。

图4 气流进入扩压器时冲击损失示意图Fig. 4 Incidence losses at the diffuer
与叶轮处冲击损失Δhii求法同理,可求得扩压器处气体冲击损失为
(13)
为简化模型,根据文献[9]可假定Ca2=Ca1,有
(14)
结合图4中几何关系与式(13),可得
(15)
其中:σ为滑移系数,为出口处气流切向速度与叶轮切向速度U2之比;β2b为叶片出口角度;D1为入口平均直径;D2为出口平均直径。
2) 表面摩擦损失。在气体流经叶轮和扩压器时,气流与叶轮壁和扩压器壁间的摩擦会导致气体表面摩擦损失。根据文献[10],气流在叶轮处的摩擦损失可定义如下
(16)
其中:l为流经通道长度;D为管道水力直径;f为摩擦因子,其取决于雷诺数Re。
圆形光滑管道Re可取2 500,此处选用布拉修斯公式计算摩擦因子,有如下关系
f=0.316 4/Re0.25
(17)
由式(16,17)可得,气体在鼓风机内摩擦损失,独立于电机转速,而与流量的二次方成正比,故可简化模型为
Δhfi=kfim2
(18)
气流在流经扩压器时的摩擦损失模型,也可由相似方法建立[11],模型如下
Δhfd=kfdm2
(19)
其中:kfi,kfd分别为气体在叶轮处和扩压器处摩擦因数。
3) 叶片负荷损失。叶片负荷损失是由于叶片间压力梯度造成气流二次流而产生的[12]。二次流是流体在流动时,存在使其偏离主流流动方向的力(如重力、离心力等)或边界条件(如弯管曲道或凹凸不平的边壁),流体随之产生的偏离主流流向的流动或偏移[13]。
叶片负荷损耗模型[14]可由如下公式给出
(20)
其中:Df为扩压因子。
综上可得,气流流经鼓风机过程中,主要总损失Δhloss为
Δhloss=Δhii+Δhid+Δhfi+Δhfd+Δhbl
(21)
1.2 气流沿直管流动阶段数学模型
对于图2(b)所示气流沿直管流动阶段Ⅱ,压力为p02的气体经圆形直管道流动至弯管入口,在这个过程中,由于管道内壁摩擦气体会产生沿程压力损失,故对于弯管入口时压力为p03,有如下关系
(22)
其中:Lc为风机出口到节流阀处管道的长度;ρ02为管道内气体密度;Δpλ为直管内气体沿程压力损失;λ为沿程阻力系数,通常取64/Re;v为管道内气体流速。
1.3 气流沿弯管流动阶段数学模型
对于图2(b)所示气流沿弯管流动阶段Ⅲ,压力为p03的气体经弯管改变流向经出口管道输出,相对在直行管道流动,弯管处气体流经距离较短,故忽略此处沿程压力损失,其损失主要来自气体经弯管改变流向造成的局部压力损失,输出压力为p,有如下关系
p=p03-Δpζ=p03-ζρ02v2/2
(23)
其中:Δpζ为弯管处局部压力损失;ζ为局部阻力系数。
结合以上所推导模型公式,最终可得风机管道系统出口输出压力与电机转速和气体质量流量关系。系统模型如下
(24)
2 出口压力控制策略
电机控制器主要由两部分组成:在转速小于6 kr/min时,调制方式为脉冲宽度调制(pulse width modulation,简称PWM),由DSP产生特定占空比的PWM波控制三相逆变器,从未改变定子相电压;当电机转速大于6 kr/min时,调制方式为脉冲幅度调制(pulse amplitude modulation,简称PAM),通过调节可控硅整流器,改变母线电压,实现电机调速目的。
在控制系统过工作时,给定所需压力值,鼓风机工作时,通过管道上的压力、流量及温度传感器,由数据采集系统采得当前状态下鼓风机状态量,经系统模型计算出当前状态下对应的参考转速,并将出口压力与设定标准压力值做差后经过比例积分(proportional & integral,简称PI)控制器,控制器输出结果叠加到计算所得参考转速中,实现出口压力闭环控制。参考转速,经转速PI控制器,即可得到母线参考电压U。通过控制器局域网络(controller area network,简称CAN)通信,将参考电压发送给三相可控硅触发板,即可完成对可控硅导通角的控制。调节母线电压,改变电机转速,实现在不改变管道阻力情况下控制输出口压力。
系统控制方案框图如图5所示。
由图中控制方案可得出,该控制策略稳态精度取决于所建立风机数学模型精准度,下面将通过实验对风机数学模型的准确性进行验证。

图5 控制系统结构图Fig. 5 Control system
3 模型有效性实验验证
3.1 实验平台
本实验平台30 kW磁悬浮高速离心式鼓风机如图6所示,数据采集系统是基于西门子可编程逻辑控制器(programmable logic controller,简称PLC),型号为S7-200。采样频率为0.5 Hz。

图6 实验平台Fig. 6 Experiment platform
3.2 实验结果
对于式(24)中参数,做如下取值:滑移系数σ取值与叶轮叶片数量相关,取为0.875;扩压器入口直径D1为0.15 m,D2为0.25 m,定压比热容cp取为1.005 kJ/(kg·K),气体绝热指数κ取值为1.41;圆形光滑管道雷诺数取为2 500,故沿程阻力系数λ取为0.021 6,局部阻力系数ζ取为0.25;kfi,kdi为气体摩擦常数,与气体速度平方正相关,气体速度可由式(11)利用其质量流量计算得出。管道入口处温度T0和气体质量流量m可由相应数据采集器在实验中采集,气体密度取值为1.200 5 kg/m3;叶片入口与出口角度β2b和β2b分别为45°和41°;直管长度LC为5 m,管道直径为0.25 m,可计算得相应气体流动横截面积。
实验时,控制电机转速逐渐增加,从6 kr/min升至26 kr/min,转速每变化200 r/min所采相应的管道出口压力数据求其均值后,最终得到100组数据,计算改进模型与原模型在每组数据对应转速下的输出压力理论值,将理论计算所得曲线与实验所测转速压力关系进行对比,结果如图7所示。
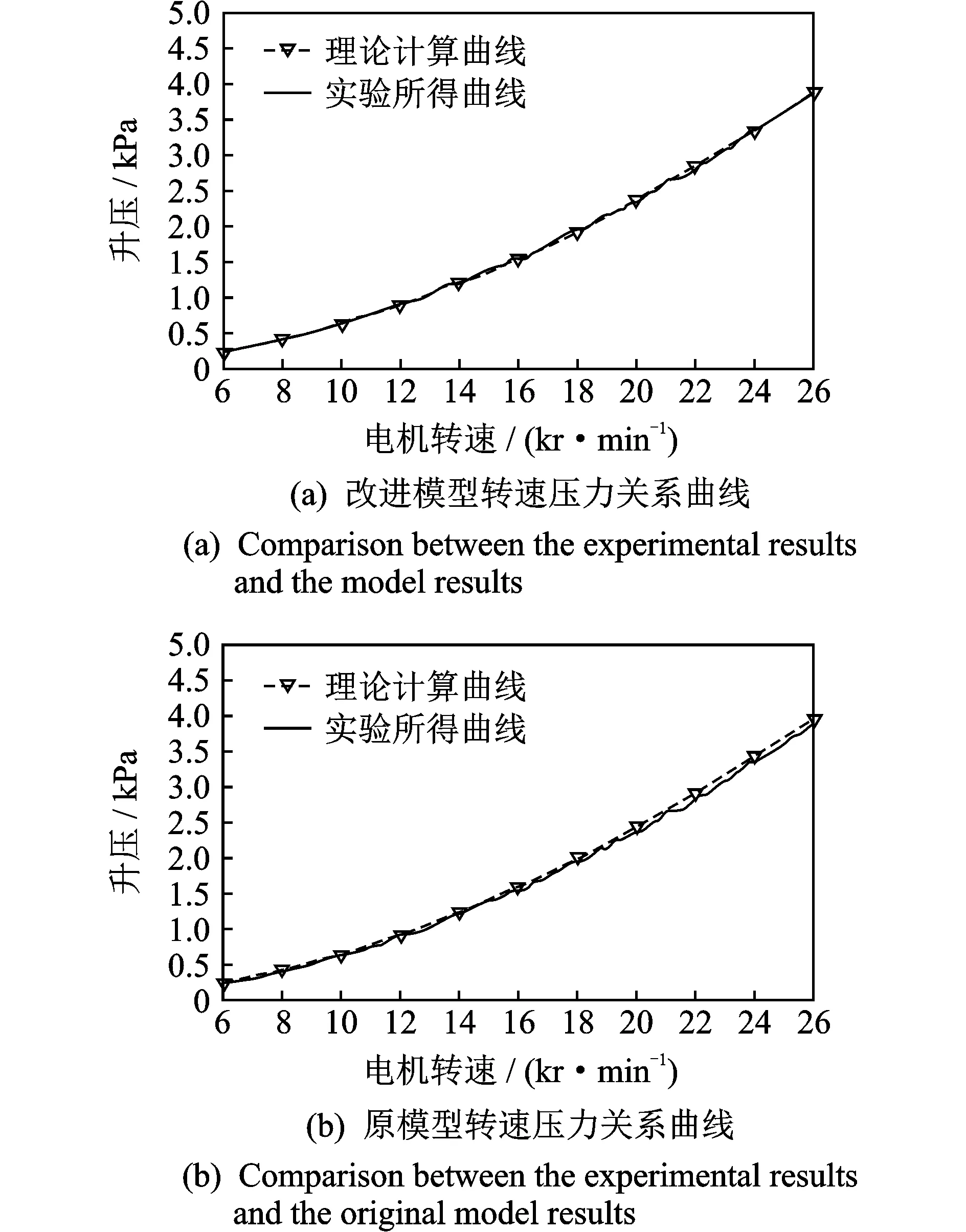
图7 不同模型压力曲线对比图Fig. 7 The relationship between rotor speed and outlet pressure for different model
计算两个模型所得压力与实验压力数据在各采样点处相对误差,结果如图8所示。

图8 不同模型结果相对实验压力数据压力误差曲线图Fig. 8 The relative error between model and experiment for different model
3.3 实验结果分析
对于鼓风机,可根据其输出风压范围将其分为低压、中压和高压风机。当管道出口压力(升压)小于1 kPa时,为低压风机;大于1 kPa、小于3 kPa时,为中压风机;大于3 kPa时,为高压风机。由图7分析可得,实验所用鼓风机,在电机转速小于13 kr/min时,输出压力属于低压范围;转速大于13、小于23 kr/min时,输出压力处于中压范围;转速大于23 kr/min时,输出压力属于高压范围。
相比图7(b),图7(a)改进后的风机系统模型,理论计算所得电机转速-压力关系曲线与实验所得曲线整体重合度较好。由式(24)可知,管道内压力损失Δp与气体质量流量m二次方相关,而m是与电机转速ω正相关的,故当转速越大时,Δp越大,不考虑管道内压力损失的风机模型计算所得理论曲线与通过实验所得实际出口压力-电机转速关系曲线的偏差就会越大。在图7(b)中,电机转速大于13 kr/min,即鼓风机管道出口压力处于中高压阶段时,两条曲线重合度较差,并且理论计算所得值会大于实际所测值。
由图8分析可得,在鼓风机输出压力为低压,即电机转速小于13 kr/min时,图8(a)中,改进模型理论计算值与实验所得值相对误差范围为±4%;而图8(b)中,不考虑管道压力损失的原模型相对误差最高可达9%。在电机转速大于13、小于23 kr/min,即鼓风机输出压力处于中压阶段时,图8(a)中改进模型对应的理论与实验值相对误差为±3%;图8(b)中初始模型对应的初始模型,其相对误差范围为±5%。在电机转速大于23 kr/min时,鼓风机输出压力处于高压阶段,此时图8(a)中改进模型对应的相对误差范围为±1%;图8(b)中初始模型的相对误差范围为±2.5%。
通过对图8中相对误差的比较分析可得,改进模型的精准度整体要高于初始模型,尤其在低速低压输出阶段效果最好,能达到5%的优化;在中高速阶段,输出压力达到1 kPa以上时,此时虽然理论值与实验值误差增大,但由于输出压力升高,相对误差反而变小,在中压输出阶段,改进模型精度提高了±2%,在高压输出阶段,精度提高了±1.5%。由此可得,改进模型在低压输出阶段精度提升显著,在中高压输出阶段精准度也有明显提升。
4 结束语
通过对Greitzer模型的改进,结合实际使用条件,去掉对使用环境要求高的容腔,增加应用中不可避免的弯管,对于该种风机管道,建立了一个考虑管道沿程压力损失和局部压力损失、以转速作为控制量的数学模型,并通过实验验证了模型的有效性和准确性。经计算比较得出,在输出压力为中压和高压阶段,相比于实验结果,所提改进模型输出压力相对误差分别为±3%和±1%,而未考虑管道损耗的风机模型这两项误差分别为±4%和±2%,均高于厂家的改进风机管道模型,这证明改进风机管道模型在精准性上有所提升。本研究所建立的模型,不仅可用于出口压力控制,在需要控制特定输出流量、对出口压力要求精度不高的使用条件下,可以通过模型变换、建立电机转速与出口流量的数学模型,完成出口流量控制,使模型具有较高的实用价值。

