面向稳态过程的基于合格品率估计的最优CSP-T边界方案
(西北工业大学 管理学院设计管理研究所,西安 710129)
0 引言
控制技术进步使得过程稳定性不断提高,为满足客户需求的多样化和将加工成本控制在可承受的范围,制造企业会将过程能力稳定在质量和成本都可接受的水平。各种过程控制工具,如统计质量控制[1,2]、过程能力指数[3,4]、制造过程知识管理[5]、连续抽样检验[6,7]、预防性维护[8,9]等,都只能独立地对稳态过程某个方面的状态做出判定,如过程能力指数判定设备加工能力对产品设计需求的满足程度,连续抽样检验在降低不合格品率同时发现过程波动等,都无法做到针对不同类型的加工过程设计个性化的控制方案,特别是目前制造业普遍存在的稳态过程。
连续抽样检验是过程控制中重要的计数检验工具。Dodge[10]提出了连续抽样检验方案,被命名为CSP-1。为适应过程稳定且质量水平较高的加工过程的质量控制需求,Liberman[11]提出多水平连续抽样方案。多水平连续抽样检验方案在我国国标GB/T 8052-2002[12]中被命名为CSP-T。CSP-T属于典型的放宽型检验方案。对于质量水平较劣的加工过程,研究者们也提出了加严的连续抽样方案[12,13]。为适应制造业自动化和信息化的变革,新的连续抽样检验方案不断被提出[6,7,14]。我国于2002年制订了GB/T 8052-2002《单水平和多水平计数连续抽样检查程序及表》[15]。国标包含了五类连续抽样方案:CSP-F、CSP-1、CSP-2、CSP-V和CSP-T。
连续抽样检验方案尽管类型多样,但都是在平均检出质量极限(AOQL)等值面上制定检验方案,称为AOQL等值面方案。实践中,各种标准(包括我国国标)均规定以生产批量为依据为生产过程选择检验方案。在AOQL等值面上制订检验方案和依据生产批量选择检验方案的策略,对于稳态过程,会造成平均输出质量合格但不一致,这不符合过程控制理念。平均检出质量不一致的原因在于在检验方案的制定过程中,没有考虑可以被视为常量的稳态过程的加工特征。
加工过程的稳定性可从过程能力指标(Cp,Cpk,Cpm,Cpmk,Spk,Pc)的波动特征得到反映。稳态过程的过程能力指数(Cp,Cpk,Cpm,Cpmk,Spk)的估计量及其分布已得到充分的研究[3,4,16,17]。过程合格品率pc是顾客最为关注的质量指标,因此也是生产控制中最重要的控制指标。CSP方案的制定是以pc为常数为前提,其控制目标也是提高pc。pc架起了稳态过程控制和CSP控制策略之间的桥梁,重新设计面向稳态过程的CSP方案时,首选参数pc为稳态过程的状态表达参数。指标pc的点估计和置信下限的研究已经趋于成熟,研究文献包括[18~22]。这些研究成果为面向稳态过程重新设计CSP-T方案提供了条件。
1 稳态过程的过程合格品率的估计和置信下限
过程合格品率pc指过程加工数据落在规定的公差范围内的比率。假设加工数据服从某种分布,其累积分布函数为F(.),则pc=F(USL)-F(LSL)。加工过程数据最常见的分布形式是正态分布,正态分布过程pc的计算公式如下:

µ是过程均值,σ是过程方差。µ和σ一般都是未知变量,需要通过样本均值和样本方差S进行估计,其中,,n是样本尺寸。用样本估计的pc可以表达为:


pc越大越好,因此,不需要研究的置信上限,置信下限成为研究者们关注的目标。文献[18~20]研究了的置信下限。Perakis等[20]改善了Wang等[19]建立的的置信下限:
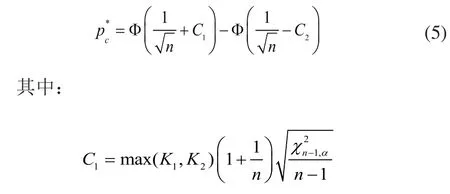

2 最优CSP-T边界方案
2.1 边界方案恒等式
范永亮[23]发明转移概率流图方法,成功地推导出CSP-T的平均检出质量公式:

p是过程不合格品率,i是连续合格品数,f是抽样分数,pc=1-p,0<p<1,0<f≤1,i>0,i只取正整数。从式(6),可以得到i和f关于AOQ的偏微分方程:


对于p(pc=1-p)为常数的稳态过程,在给定的质量需求AOQL下,满足等式(9)的所有(i,f)组合,都能使稳态过程获得输出质量AOQ=AOQL,称这些检验方案为稳态过程的边界检验方案,命名为(imin,fmin)。因为AOQ是关于i和f的减函数,所以对于特定稳态过程的所有边界方案,当i>imin且f>fmin,AOQ<AOQL;当i=imin且f>fmin,AOQ=AOQL;当i<imin且f<fmin,AOQ>AOQL。满足等式(9)的(imin,fmin)组合有无穷多个,因此,边界方案有无穷多个。
用绩效指标AOQ衡量稳态过程边界方案的绩效,发现边界方案可以分为三类,如图1所示。第一类和第二类方案有无穷多个,第三类方案只有一个。图1显示了这三类方案的AOQ曲线。显然,只有第三类方案,无论过程质量改善还是恶化,都能获得合格的输出质量。
对于稳态过程,在所有边界方案中,第三类方案是唯一的可行方案,称为最优CSP-T边界方案。最优方案满足等值面条件。因此,需要寻找等值面方案满足的恒等式,以求解最优方案参数。

图1 给定质量需求AOQL下三类边界方案的AOQ曲线
2.2 等值面方案恒等式
CSP-T在AOQL等值面上建立检验方案,根据生产批量为稳态过程选择检验方案,导致能力不同的多个并行稳态过程输出质量不一致。假设三台设备服务于一道工序,三台设备的过程能力相同且具有相同的p,生产批量不同。分别为三台设备选择三个不同的CSP-T的AOQL等值面方案。图2展示了三个方案的AOQ曲线。显然,AOQ1≠AOQ2≠AOQ3。输出质量合格但不一致。

图2 给定质量需求AOQL下等值面方案的AOQ曲线
从式(6),可以得到AOQ关于p的偏微分:

从式(7)和式(10),得到:

从式(8)和式(10),得到:


满足恒等式(13)的所有解(i,f,p)(p=1-pc)是CSP-T的AOQL等值面方案。式(13)即是所要寻找的满足等值面条件的恒等式。
2.3 最优方案参数求解
将最优CSP-T边界方案参数记为(io,fo),则式(9)和式(13)可以改写为:
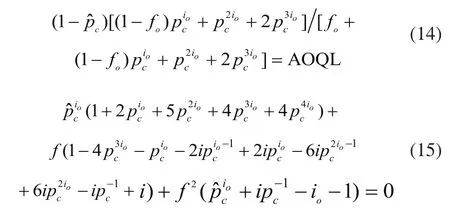
联立求解式(14)和式(15),得到面向稳态过程的最优CSP-T边界方案参数,式(14)和式(15)的解唯一,说明最优边界方案唯一。
最优CSP-T边界方案的AOQ曲线如图3所示。从图3可以看出,最优CSP-T边界方案既满足边界条件又满足等值面条件,能够实现定量输出控制,对改善和恶化的过程波动都能加严控制。

图3 给定质量需求AOQL下稳态过程的最优CSP-T方案的AOQ曲线
3 最优CSP-T边界方案与CSP-T方案的比较
图4~图6为最优CSP-T边界方案和CSP-T方案的OC,AFI,AOQ曲线。比较了服务于同一工序的两台设备,加工数据都服从正态分布。输出质量需求AOQL=0.00018。pc置信下限的置信水平a=0.1。过程一:K11=3.59,K12=3.59,p1=0.00038。过程二:K21=3.49,K22=3.49,p2=0.000452。分别依次运行式(5)、式(14)和式(15),得到:p*c1(a=0.1)=0.998935,(io1,fo1)=(6531,0.1016);p*c2(a=0.1)=0.998535,(io2,fo2)=(1650,0.8033)。两个过程原来采用的CSP-T方案是(i,f)=(14706,0.01)。
从图4可以看出,无论过程质量改善或者恶化,最优CSP-T边界方案都能加严控制且输出质量可量化控制,AOQo1=AOQo2=AOQL=0.0018。对于多个并行过程控制,最优CSP-T边界方案优势显著。CSP-T方案能够得到合格的输出质量,AOQ1<AOQL,AOQ2<AOQL,但AOQ1≠AOQ2,不同稳态过程输出质量不等且不能量化,不符合现代过程控制的理念。

图4 过程能力不同的两个稳态过程的最优CSP-T边界方案和AOQL等值面方案的AOQ曲线

图5 过程能力不同的两个稳态过程的最优CSP-T边界方案和AOQL等值面方案的AFI曲线

图6 过程能力不同的两个稳态过程的最优CSP-T边界方案和AOQL等值面方案的接收概率曲线
图5的AFI曲线显示,最优CSP-T边界方案的AFI低于CSP-T方案。说明最优CSP-T边界方案能以较低的检验工作量实现输出质量的定量控制。
图6的OC曲线显示,L(p)o1>L(p)1,L(p)o2>L(p)2,最优CSP-T边界方案的接收概率都高于CSP-T方案。这个结果与实际情况是相符的。对于需要用CSP-T进行控制的稳态过程,实施检验后,输出过程质量符合质量需求,应该以高的概率接收。
4 应用实例
主轴是空调压缩机的核心零件。短轴外径精磨工序是主轴加工的关键工序。外径精磨有两台磨床。短轴外径尺寸为17.976±0.004mm,上公差限17.98,下公差限17.972,目标值17.926。输出质量需求AOQL=0.00018。工序现采用CSP-T的(i,f)=(6573,0.1)进行过程质量控制。根据实践经验,精磨工序质量稳定,拟采用最优CSP-T边界方案控制工序输出质量。各收集两台设备的100个数据,分别列入表1和表2。图7和图8是正态概率图和正态柱状拟合图。加工数据近似服从正态分布。
设备一不必执行连续抽样检验。设备二执行最优CSP-T边界方案。在检验过程中,保持100个最新的检验数据,并计算c2。如果c2≥0.998603,检验方案继续。如果c2<0.998603,则根据式(14)和式(15),调整最优CSP-T边界方案参数。
表3列出了两台设备的短轴精磨工序在最优CSP-T边界方案和CSP-T方案下的三个绩效指标:AOQ,AFI,L(p)。最优CSP-T边界方案判定设备一相比于质量需求,具备高的过程能力,免检,减少了检验工作量。设备二执行最优CSP-T边界方案后,AFI降低且接收概率提高。
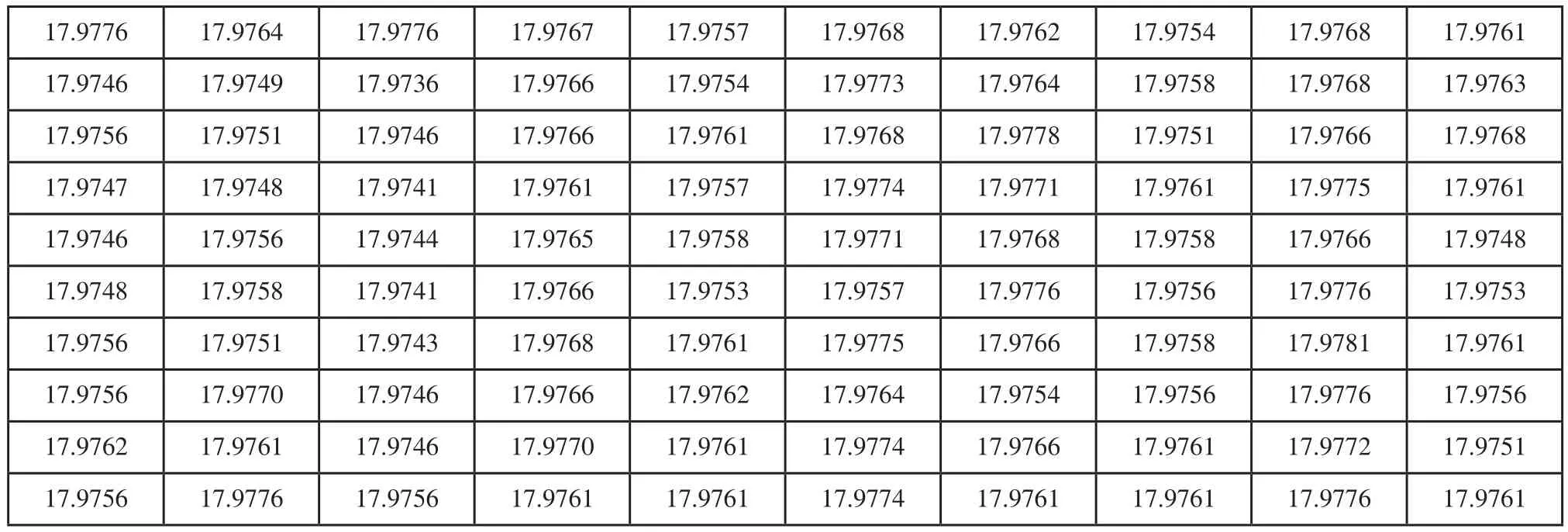
表1 设备一的100个短轴外径数据

表2 设备二的100个短轴外径数据

表3 最优CSP-T边界方案与等值面方案下的绩效指标对比

图7 设备一样本数据的正态概率图和柱状图
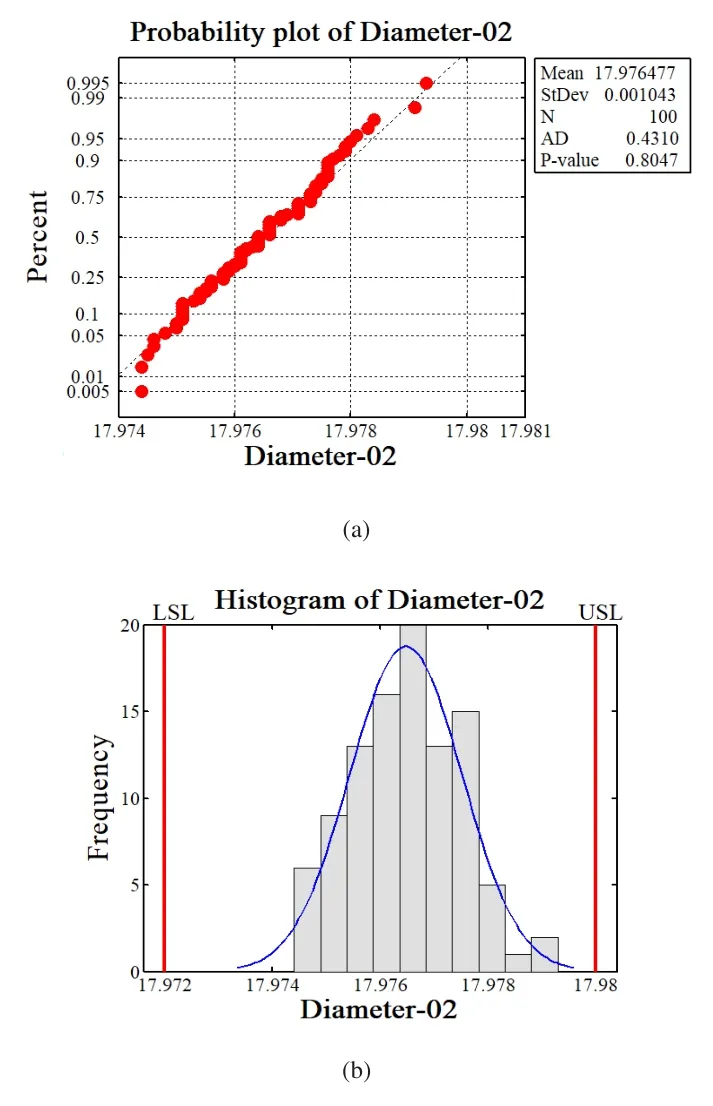
图8 设备二样本数据的正态概率图和柱状图
5 结论
面向稳态过程的基于合格品率估计的最优CSP-T边界方案,是根据稳态过程特征,对CSP-T检验方案选择方法的重新设计。最优CSP-T边界方案具有下列优异属性:是面向稳态过程的唯一最优边界方案;精准控制输出质量;能够保证服务于同一工序的多个能力不同的并行过程输出质量相等;建立了方案参数(io,fo),质量控制指标AOQL,检验数量指标AFIO(可代表成本指标)和稳态过程指标pˆc的一一对应关系;对于加严和改善两个方向的过程质量波动均能加严控制;能够根据过程质量波动调整检验方案。最优CSP-T边界方案的运作特征相比于CSP-T,更加符合现代过程控制的理念:量化,精准,可预测。

