基于Matlab/Visual Basic的客车行李舱门气弹簧选型设计

张普晖， 杨红华， 窦振山， 郑 能

(中国重汽集团技术发展中心， 济南 250100)

气弹簧是客车行李舱门上的重要附件之一，具有支撑、缓冲、制动、高度调节及角度调节等功能。气弹簧的伸展力选定直接影响到舱门的功能使用[1]，若伸展力过小，会导致舱门无法自如打开至设计的最大开启角度，影响舱体内部行李取放和舱体内元器件检修等；若伸展力过大，会导致舱门开启速度过快、开启后受力变形、舱门开关费力等，极大地影响交互体验。本文结合实际案例，建立舱门开启过程中门体开启角度与气弹簧伸展力关系的数学模型，通过Matlab 软件进行数学分析和图像转换，得到最优的气弹簧伸展力，并验证舱门关门力；通过开发舱门气弹簧的选型工具，提升舱门设计的工作效率。

1 舱门气弹簧的计算与校核

在进行舱门气弹簧的计算与校核之前，需确定气弹簧的装配位置，其合理性的判定依据是：气弹簧在舱门闭合状态下的倾斜角度β(指气弹簧与竖直线的锐角夹角)不小于3°，该状态可以保证在不对舱门施加外力时，气弹簧伸展力矩T1能使门体处于关闭状态[2-4]。

1.1 几何模型

为便于分析气弹簧伸展力与门体开启角度的力学关系，建立舱门-气弹簧系统的简化几何模型如图1所示。

图中，A表示舱门AL旋转轴，B表示A点在气弹簧JD延长线上的投影点，C表示气弹簧上固定点在舱门AL连线上的投影点，D表示气弹簧上固定点，E表示舱门AL重心在Y轴上的投影点，H表示舱门重心，L表示舱门远离旋转轴的端点，M表示气弹簧JD延长线和舱门AL直线的交点，J表示气弹簧下固定点，K表示气弹簧下固定点在Y轴上的投影点。

(a)舱门关闭状态

令舱门门体长度AL=a，舱门门体重量G，舱门门体重心距旋转轴距离AH=b，气弹簧上固定点在门体旋转轴与门体下端点连线(以下简称门体直线)上的投影点与旋转轴之间的距离AC=c，气弹簧上固定点与门体旋转轴与门体下端点连线之间的距离CD=d，气弹簧下固定点与旋转轴之间的水平距离JK=e，气弹簧下固定点与旋转轴之间的竖直距离AK=f，气弹簧数量n，气弹簧压缩行程s，气弹簧最大设计长度l。

1.2 气弹簧标称伸展力计算

为便于分析，此处忽略转轴本身的转动摩擦力，定性地分析舱门开启的过程，大致分为以下3个阶段：

阶段一，开启角度α从0°到某临界角度α1，气弹簧收缩，压缩力在旋转轴A上的力臂由大变小逐渐趋于0，该过程中，气弹簧阻碍舱门开启，人需要施加开门力矩T2：

α1=arctand/c-arctane/f

(1)

F·n·h+G·b·sinα-T2=0

(2)

阶段二，开启角度α从α1到另一临界角度α2，气弹簧伸展，伸展力在旋转轴A上的力臂由0变大，直至力矩与重力力矩达到平衡，此过程中，气弹簧帮助舱门开启，但人仍需施加开门力T2：

F·n·h-G·b·sinα-T2=0

(3)

阶段三，开启角度α从α2到最大设计角度，气弹簧伸展，伸展力在旋转轴A上的力臂逐渐变大，此过程中，气弹簧帮助舱门开启，人不需施加开门力，舱门自动开启。此时需要满足：

F·n·h-G·b·sinα>0

(4)

设计中，只需要施加较小的开门力使舱门开启到最大设计角度，即认为开门力矩近似为零，对阶段二和阶段三合并作受力分析，可以得到：

F·n·h-G·b·sinα=0

(5)

即：

F=G·b·sinα/(n·h)

(6)

式(6)即为使舱门达到平衡状态所需的气弹簧伸展力F与开启角度α的关系式。

其中，h为气弹簧伸展力对旋转轴A的力臂，它可用式(7)表示：

(7)

式7的推导可采用向量法，即建立以A点为原点的平面直角坐标系，则依次可得以下各点的坐标及向量的表达式：

C(c·sinα,-c·cosα)

J(-e,-f)

则可根据式(8)计算气弹簧与水平线夹角∠DJK的表达式。

(8)

同时可根据式(9)计算门体旋转轴、气弹簧下固定点连线与水平线夹角∠AJK的表达式。

∠AJK=arctane/f

(9)

进而根据∠AJB=∠AJK-∠DJK计算气弹簧与门体旋转轴、气弹簧下固定点连线夹角∠AJB的表达式，在ΔAJB中，利用三角函数可得式(7)。

为了分析所需伸展力F与舱门开启角度α的关系，使用Matlab软件绘制函数曲线图如图2所示[5]，其中开启角度α取值范围α=(α1,3π/4)(设计最大开启角度)，其余参数值结合设计实例测得：G=150 N；AL=1.158 m；b=0.56 m；c=0.127 m；d=0.062 m；e=0.03 m；f=0.576 m；x=0.012 m；n=2；j=0.61 m。

图2 所需伸展力F与舱门开启角度α的关系

图2还不能直接指导确定所需要的气弹簧标称伸展力参数，原因是气弹簧输出的伸展力随压缩行程的变化而变化，通常将气弹簧所能输出的最小伸展力，即气弹簧接近最大设计长度时输出的力，作为气弹簧的标称伸展力。

气弹簧的工作原理决定了气弹簧的弹性系数几乎为一个定值，通过查阅相关的资料[6]，这个数值通常为1.2～1.4 N/mm。在本设计中，设定气弹簧弹性系数k=1.4 N/mm。

根据式(10)求压缩行程s与开启角度α的关系式。

(10)

进而根据式(11)求所需气弹簧标称伸展力F1与开启角度α的关系式，并运用Matlab绘制函数曲线如图3所示。

F1=F-103·k·s

(11)

图3 所需标称伸展力F1与舱门开启角度α的关系

由图可知，函数值先从无限大逐渐减小，然后又逐渐增大。由于不可能将气弹簧的标称伸展力参数选得无限大，所以选取波谷以右的极大值作为应选择的气弹簧标称伸展力参数。

需要说明的是，在本例中，应选气弹簧标称伸展力参数和所需最小气弹簧伸展力刚好相等，且均为开启角度为最大设计角度时的函数值，但并非每例如此，所以，计算过程不能省略。

1.3 人所需施加的关门力校核

同分析开门过程时一样，不考虑转轴本身的摩擦力，但将压缩行程相等时气弹簧的伸展力和收缩力的差值纳入考量，这个差值的形成因素主要是气弹簧自身的摩擦力和阻尼[7-8]，通过查阅资料，在本例中近似取一个定值80 N。

根据式(12)计算关门力F2与开启角度的关系式，其中，F3代表气弹簧收缩力，F1代表所选的气弹簧标称伸展力参数，本例中取275 N，并运用Matlab绘制函数曲线如图4所示。

F2=(F3·n·h-G·b·sinα)/a=
[(F1+k·s+80)·n·h-G·b·sinα]/a

(12)

图4 关门力F2与舱门开启角度α的关系

其最大值41 N，即人所需施加的最大关门力为41 N，经判定符合80 N以下的适宜范围[9]。如果计算所得的关门力过大，则需要通过调整气弹簧设计长度和安装位置来优化，此过程本文不涉及。

2 编写GUI用户界面

为便于选择合适的气弹簧，使用VB语言开发气弹簧伸展力参数计算程序和用户界面。在舱门门洞尺寸和舱体内部结构确认时，舱门的铰链和密封结构均已确定，舱门的其余参数值亦可由三维模型测量得到，通过输入上述参数值即可得到设计需要的气弹簧伸展力，同时校核所需的最大关门力，并最终确定气弹簧类型。该程序计算简便，通用性好，通过修改相关参数可得到不同类型舱门所需要的气弹簧伸展力和最大关门力，界面如图5所示[10-12]。

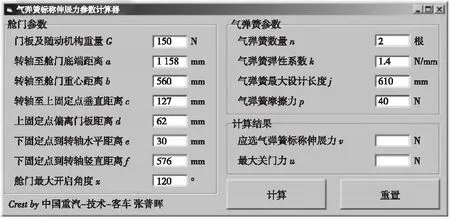
图5 气弹簧伸展力参数计算程序和用户界面

3 结束语

本文结合客车结构实际建立舱门-气弹簧系统数学模型，综合伸展力、弹性系数、开启角度、摩擦及阻尼等各项影响因素推导出理论分析公式，借助Matlab及Visual Basic等计算机软件得出分析结果并制作用户操作界面，有效辅助设计者对气弹簧的选型工作。