某轻型客车横置板簧式麦弗逊悬架刚度分析

狄 帅， 李明安， 张训福

(潍柴动力股份有限公司 上海研发中心客车所， 上海 201114)

随着车管政策对货车的限制越来越严格，厢式轻客代替了部分被限制进城的轻卡，未来用于校车的宽体轻客在二三线城市也会更加广泛地应用[1]。底盘悬架系统方面，一部分VAN类轻客的前悬架采用独立悬架，包括双横臂式和经典螺旋弹簧麦弗逊式独立悬架等[2-3]。

经典螺旋弹簧麦弗逊式悬架又称滑柱摆臂式悬架，其弹性元件为螺旋弹簧[4-5]。近年来，采用横置板簧(可以是钢板弹簧，也可以是复合材料板簧)代替螺旋弹簧的变型麦弗逊悬架广泛应用在某些轻型客车的前悬架上。然而目前针对此横置板簧式麦弗逊悬架的研究并不多，影响了相关弹性元件的匹配选型工作。本文对横置板簧式麦弗逊悬架的刚度进行研究分析。

1 悬架刚度计算模型的建立及刚度计算

1.1 悬架刚度计算模型的建立

图1为横置板簧式麦弗逊悬架的结构型式：下摆臂3内侧通过螺栓与副车架铰接在一起，外侧与转向节2下部相连，转向节2上部与滑动立柱固定，并沿减振器1的活塞杆上下滑动。横置板簧7代替传统的螺旋弹簧成为整个悬架系统的弹性元件：其外侧靠端部橡胶垫4与下摆臂3接触，内侧则固定在上橡胶垫6和下橡胶垫5之间，上橡胶垫顶在副车架上，下橡胶垫顶在压板上。

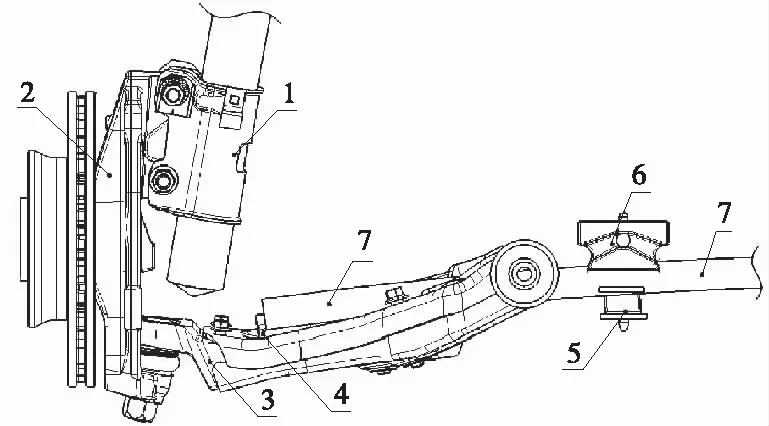
1—减振器； 2—转向节； 3—下摆臂； 4—端部橡胶垫；5—下橡胶垫； 6—上橡胶垫； 7—横置板簧

建立横置板簧麦弗逊悬架的刚度计算模型。与螺旋弹簧麦弗逊悬架的刚度计算模型相比，本刚度模型的主要变化在于弹性元件位置的变化：原螺旋弹簧的受力沿减振器轴线方向，而本模型中，弹性元件的受力垂直于下摆臂。使用图解法来求横置板簧式麦弗逊悬架中车轮和转向节总成与车身的瞬时运动中心M，如图2所示。设大地为构件1，车轮和转向节总成为构件2，下摆臂为构件3，减振器为构件4，车身为构件5，横置板簧和3个橡胶垫组成的复合横置板簧系统为构件6(1-5为刚性构件；6为弹性构件，其刚度为k)。根据机械原理相关知识[6]，很容易确定部分两构件之间的瞬心位置，如P12、P23、P35和P45。根据三心定理，构件2下球铰点绕下摆臂的球铰点旋转，其瞬心P25在P23和P35的延长线上。此外，构件2上端沿减振器轴线运动，因此瞬心P24在垂直于减振器轴线无限远处，而P25在P24和P45的延长线上，即过P45作垂直于减振器轴线的直线，与上述延长线交于点M，点M即是车轮和转向节总成与车身的瞬心位置。

图2 横置板簧麦弗逊悬架的刚度计算模型

为计算悬架刚度，以图2模型为基础，在车轮与车身之间放置一个虚拟弹簧替代实际弹簧(该虚拟弹簧轴线与车轮中心线重合)，使其在车身和车轮之间传递力，这个虚拟弹簧的刚度就是要计算的悬架刚度C，如图3所示。

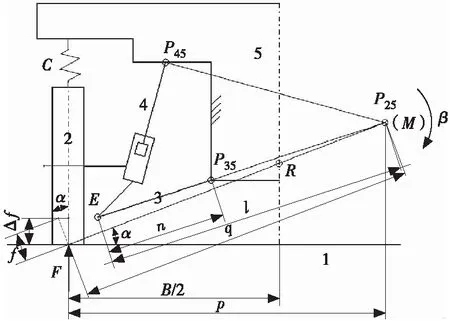
图3 横置板簧麦弗逊悬架的当量刚度计算模型

1.2 悬架刚度的计算

借助图3模型，对悬架刚度C和复合板簧系统刚度k的换算关系进行计算分析。

根据虚位移原理，假定车轮和转向节总成绕M点转动一个虚位移β，有以下关系：

FΔf=FsΔfs

(1)

式中：F是地面对车轮的垂直力增量(本模型中，假设轮胎刚度无限大)；Fs是复合板簧系统受力的增量；Δf是车轮接地点的垂向虚位移；Δfs是复合板簧垂直于摆臂方向的虚位移。Δf可以表示为：

Δf=fcosα=qβcosα=(qcosα)β=pβ

(2)

式中：f为车轮接地点沿瞬时运动方向的虚位移；α为点M与车轮接地点连线与地面的夹角；q为点M与车轮接地点连线的长度；p是点M与车轮接地点连线的水平分量长度。

下摆臂绕点P35转动时，点E的位移fE与Δfs的关系为：

Δfs=fE·m/n

(3)

式中：m为复合板簧力作用点的杠杆长度；n为下摆臂球铰点的杠杆长度。

又由于点E也是车轮和转向节总成上的一点，所以点M也是点E的瞬心，fE可以表示为:

fE=lβ

(4)

式中：l为ME连线的长度。

将式(4)代入式(3)，得：

Δfs=lβ·m/n

(5)

由β引起的车轮的垂直力增量F可以表示为：

F=CΔf=C(pβ)

(6)

由β引起的复合板簧力的增量Fs可以表示为：

Fs=kΔfs=k·lβ·m/n

(7)

将式(2)、式(5)、式(6)和式(7)代入式(1)，得：

(8)

式(8)就是横置板簧式麦弗逊悬架刚度C和复合板簧刚度k的换算关系，不过C为单边刚度，整个悬架的刚度C′=2C。

双横臂式独立悬架的换算关系为[2-3]：

(9)

从式(8)和式(9)对比可以看出，本模型的刚度换算关系与双横臂式独立悬架的公式基本一致，式(9)多了一个cosθ项，而θ是下摆臂上的弹簧与摆臂垂线的夹角，因在横置板簧式麦弗逊悬架中，复合板簧的力永远与摆臂垂直，故而θ=0°，则：

cosθ=1

(10)

将式(10)代入式(9)，即为式(8)。

然而双横臂悬架的瞬时中心M是上下摆臂连线的交点，与本模型不同，因此可以认为，横置板簧式麦弗逊悬架结合了螺旋弹簧式麦弗逊悬架和双横臂悬架的结构特点。

为了方便计算，上述计算模型中，暂时将横置板簧和3个橡胶垫组成的弹性系统当做一个复合板簧系统(其刚度为k)，下面对此复合板簧系统的刚度进行分析。

2 复合横置板簧系统刚度计算与分析

2.1 复合横置板簧系统刚度计算

选取横置板簧对称平面的一侧进行分析，横置板簧和3个橡胶垫的装配关系如图4所示。板簧端部受力Fd的状态下，上橡胶垫实际厚度为h1，压缩量为l1；下橡胶垫实际厚度为h2，压缩量为l2；横置板簧厚度为h3(认为横置板簧不可压缩)，支点处的安装空间高度为H。

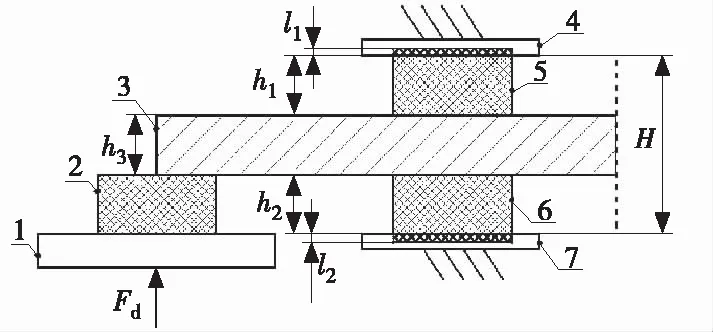
1—下摆臂； 2—端部橡胶垫； 3—横置板簧； 4—副车架；5—上橡胶垫； 6—下橡胶垫； 7—安装板

橡胶垫作为橡胶弹性元件，其刚度并不是线性的[7]。各橡胶垫因结构不同(材料也可能不同)，具有不同的加载特性曲线。为方便计算，假定3个橡胶垫的刚度为线性的，建立复合横置板簧系统的刚度模型，如图5所示。

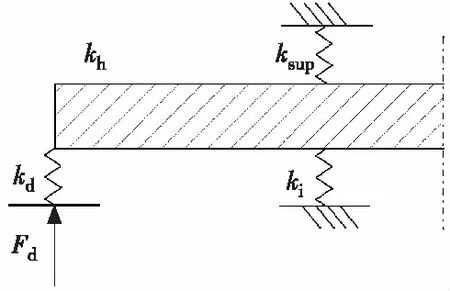
图5 复合横置板簧系统的刚度模型

通过此刚度模型分析得出，上橡胶垫和下橡胶垫并联后同横置板簧和端部橡胶垫串联，则整个复合横置板簧系统的刚度[8]如下：

(11)

式中：kh为横置板簧单边刚度；kd为端部橡胶垫的刚度；ksup为上橡胶垫的刚度；ki为下橡胶垫的刚度。

横置板簧的单边刚度kh一般为线性，而3个橡胶垫的刚度kd、ksup和ki则需要结合其加载特性曲线来求出(仅有加载特性曲线的情况下，最好借助辅助软件将特性曲线转化为具体的数据表，以方便后续工作)。

图6 某橡胶垫的加载特性曲线

从图6可以看出，橡胶垫的加载特性曲线具有明显的非线性，其刚度随着力的增大而增大。为了确定kd、ksup和ki，先求出端部橡胶垫受力Fd，将式(2)和式(5)代入式(1)，得：

Fd=F·np/(ml)=F/η

(12)

式中：η为悬架系统的杠杆比，取η=ml/(np)。

F分别取空载、满载簧上质量对应的力F1、F2，得Fd1和Fd2：

Fd1=F1/η
Fd2=F2/η

(13)

对于端部橡胶垫，通过其加载特性曲线确定其刚度为：

(14)

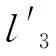
确定上橡胶垫的刚度ksup和下橡胶垫的刚度ki则相对复杂一些。结合图4分析，系统端部不受力状态下，因支点处的安装空间高度H要小于上橡胶垫自由高度(即h1+l1)、下橡胶垫自由高度(即h2+l2)和板簧厚度h3(板簧本身的厚度改变量忽略不计)之和，两橡胶垫同时受力被压缩，受力相同(Fsup=Fi)，上橡胶垫压缩l1，下橡胶垫压缩l2，且满足式(15)。

H=h1+h2+h3

(15)

端部受力状态下，端部橡胶垫受到向上的力Fd，上橡胶垫被进一步压缩，l1变大，h1变小；下橡胶垫则回弹，l2变小，h2变大，且h1的减量等于h2的增量，仍满足式(15)。此外，上橡胶垫受力Fsup变大，下橡胶垫受力Fi变小，且满足式(16)[9]。

Fd=Fsup-Fi

(16)

空载和满载时有：

Fd1=Fsup1-Fi1

(17)

Fd2=Fsup2-Fi2

(18)

式中：Fsup1为空载时上橡胶垫的受力；Fi1为空载时下橡胶垫的受力；Fsup2为满载时上橡胶垫的受力；Fi2为满载时下橡胶垫的受力。

(19)

ksup和ki可认为是上下橡胶垫在空满载载荷段的近似刚度。

将求得的kd、ksup和ki代入式(11)，即可得到此复合横置板簧系统的刚度k。

2.2 复合横置板簧系统刚度分析

取k′=ksup+ki，式(11)变为：

(20)

从采用此类横置板簧式麦弗逊式前独立悬架的轻型客车的实际使用情况来看，横置板簧的单边刚度kh约为100～200 N/mm，而橡胶垫在空满载载荷段的近似刚度能达到4 000 N/mm，甚至更大，远大于横置板簧的单边刚度。假设端部橡胶垫的刚度kd=k′且为横置板簧的单边刚度的e倍，即：

kd=k′=ekh

(21)

将式(21)代入式(20)，得：

k=e/(2+e)·kh=30/(2+30)·kh=0.937 5kh

(22)

其中e取30。此时整个复合横置板簧系统的刚度k约为横置板簧单边刚度的93.75%。当e趋向于∞时，k≈kh。

3 结束语

1) 在轻型客车上得到广泛应用的横置板簧式麦弗逊悬架的运动瞬心的确定与螺旋弹簧式麦弗逊悬架相同，而弹性元件的受力则与双横臂式独立悬架类似。

2) 计算复合板簧系统的刚度时，因橡胶垫的刚度远大于横置板簧刚度，这个串联的复合板簧系统刚度略小于横置板簧的刚度，某些情况下可直接通过横置板簧的刚度来估算复合板簧系统的刚度，从而降低匹配计算的工作量。