例谈初中几何证明中 “辅助线的自然生成

秦晓

[摘  要] 辅助线是连接已知条件和所求结论的桥梁，是在分析条件、探索结论中结合所学概念、定理、几何模型等相关知识自然联想到的所需要的帮助. 因此，在具体的教学过程中，教师要力求向学生展示辅助线的生成过程，让学生体会辅助线是怎样在问题中“无中生有”的.

[关键词] 桥梁;生成;感悟

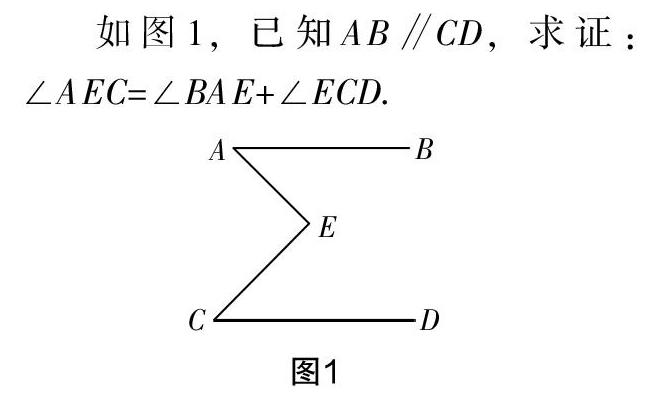
1. 从几何定理入手寻找辅助线的自然生成

分析讲解  根据“平行线的性质定理”：两条平行直线被第三条直线所截，同位角相等，内错角相等，同旁内角互补. 本题已知条件中出现了两条平行直线，要求证的结论是角度之间的数量关系，这与平行线的性质定理描述的内容高度吻合，所以我们可以从这里找到破题点. 对比定理发现，这里缺少的就是第三条截线，所以我们可以从这个角度出发添加辅助线，构造截线，接下来就只需要思考可以怎么构造截线. 这个问题抛给学生以后，辅助线就在学生笔下自己长出来了，而且还不止一种方法，展示辅助线的添加方法如下：可以过点E作直线MN∥AB，如图2;可以连接AC，如圖3;可以延长CE交直线AB于点F，如图4;可以延长AE交直线CD于点F，如图5.

启示  从定理入手，使得辅助线的出现有了“落脚点”，在熟悉、掌握定理的基础上，可以很自然地得到辅助线，这是直接告诉学生：“平行线问题中遇到拐点就过拐点作平行线”是不能相比的.后者这样直接灌输，不仅容易遗忘，而且记住的学生也大都“消化不良”，在遇到类似问题时无法举一反三.

2. 从几何模型中寻找辅助线的自然轨迹

这个问题很多学生都觉得无从下手，本来准备就这个题给学生做一个仔细的评讲，不过在评讲的时候，一位学生主动请缨，说出了她添加辅助线的过程：从这个题目要解决的问题入手，求△ADE的面积，就联系到三角形的面积公式——底乘以高除以2，那么就应该思考以△ADE的哪一边作为底. 根据已知条件，三边中已知AD边为2，所以很自然联想到过点E作EM垂直于直线AD，这样就生成了解决这个问题的第一条辅助线. 可是问题还没有彻底解决，这个时候我也思考了很久，发现DE=DC，而且还出现了两个垂直关系，所以我联想到平时学习过的“三垂直模型”，因此我尝试着过点C作CN垂直于直线AD，如图8所示. 通过△DME≌△CND，得到EM=DN，居然真的把这个题目做出来了，太让我兴奋了.一番描述行云流水，全班同学佩服得报以热烈的掌声.

启示  这道题目难度不小，但是学生的回答却给了笔者很多启发，因为每一条辅助线都来得那么自然，层层推进. 由三角形面积公式想到作高线，由高线带来的垂直关系再结合CD=DE，联系到全等中的“三垂直模型”，进一步转化已知条件. 整个解题过程一气呵成，酣畅淋漓，这不论对解题者还是参与倾听的学生来说都会受益良多，也再次感受到了辅助线的自然生成有强大的生命. 这不仅使用了老师教授的辅助线的作法，而且也让学生自己收获了运用这种思维带来的成果.

3. 从几何图形的对称美中去发现辅助线的自然生成

很多几何图形，比如角、线段、等腰三角形、等边三角形等都具有轴对称性，它们的性质，比如角平分线上的点到角两边的距离相等，线段垂直平分线上的点到线段两个端点的距离相等，等腰三角形的“三线合一”也基本上来自于其图形本身的对称性，只不过当我们研究完这些性质以后，更多的注意力放在了定理本身以至于忽略了它最本质的特性. 比如这样一个例题：如图9，在△ABC中，已知AC>BC，CD平分∠ACB，求证：AD>BD.

启示  刚分析本题时，会让人有摸不着头脑的感觉，感觉一个明显的结论就是无法通过推理得到，从而产生失落怅然. 如果能够多体会角是一个轴对称图形，就算它的性质定理也只是它的轴对称性的一个特殊角度的展示;如果能从图形本身的这种特征出发去解决问题，那么便会给我们很多题目的解决带来启发，也自然能寻找到辅助线的蛛丝马迹.

4. 从结论的形式中去体会辅助线的生成

有一类几何证明题，它的已知条件或者是结论里面有形如两条线段的和（或者差）等于第三条线段，或者一条线段是另一条线段的两倍，一个角是另一个角的两倍等之类的描述，这种形式也蕴含着解题的思路，下面用一道例题加以展示：如图11，CD为△ABC的中线，求证：CA+CB>2CD.

分析讲解  从已知条件入手似乎觉得没有更多的解题思路了. 这个时候可以从结论入手，发现结论中出现了2CD，所以可以从这里出发找到本题的突破口，尝试将CD延长加倍，延长CD至点E，使得CD=DE，然后连接AE，构造全等三角形.如图12，△CDB≌△EDA，得到CB=AE，在△ACE中，利用三边关系可得：AC+AE>CE，根据线段的等量代换得到CA+CB>2CD，得出证明.

启示  很多教辅书中都将这种方法称为“中线倍长法”，笔者认为，除了介绍这种名称外，更重要的是带领学生一起去感悟“中线倍长”字面之外的含义，什么时候需要中线倍长？将中线倍长以后会得到什么样的结论？这些结论结合其他常见的几个图形又会出现哪些常见的问题？这样学生才会知道在哪些情况下需要把线段进行倍长，而不至于为了倍长而倍长，把某些简单的题目反而复杂化.

辅助线的添加对于一道几何题目而言是一个系统工程，每一种方法之间也不是孤立的，每一个学生看到一个已知条件联想到的知识点也是不尽相同的，所以从每个人的思维之数上开出的花就是五彩缤纷的，这也形成了课堂的多样变化深度以及广度，让每个学生在与别人的交流中碰撞思维（图9的例题），在实际的授课中有的学生是从定理入手得到解决方案的，现在将他的思路展示如下：

看到已知条件中出现了角平分线，我首先想到的就是角平分线定理，所以我尝试了做角两边的垂线段. 如图13，过点D作DE⊥AC，DF⊥BC. 接下来我发现，除了得到DE=DF便无路可走了，再仔细一想，作了垂线段以后可以联系到三角形的面积，尝试这样一思考，利用=，同==，进而得到=，因为AC>BC，所以AD>BD.

1. 关注学生的学情，用已经掌握的知识推动思维的发展

学生才是学习的主体，教师所做的工作是为主体服务的. 这就需要我们深入了解我们的主体，知道他们现有的知识近区，加以引导，扩大他们的认知圈，为推动下一步的思维发展奠定基础. 如果忽略了，不管教师自认为讲解得多么透彻，学生听来都是云里雾里，不知所云，更不用说知道学习了.

2. 教学过程注重“慢”的艺术

世间万事的生成都是有过程的，需要时间的，所以在教学的过程中要有留白，有安静的思考，有火热的讨论，有条理的交流，这些都需要执教者有从容的心态，不怕学生花时间. 这样的课堂可能例题的讲解数量比较少，可是涵盖的知识容量，以及衍生出来的学生对数学的兴趣、感知的数学的活力、思维能力的提升等非智力因素却会带来事半功倍的效果.

3. 教学过程中注重学生模型思维的培养

在几何证明中有很多从一般情况中提炼归纳出来的模型，可以强化这种模型意识，就是强化学生对概念、定理等知识的深入认识，让学生少走弯路，提高成功的体验率，有了一次次推理成功的通畅淋漓的感觉，学生學习数学的激情必定高涨，内驱力带来的效果是任何说教都替代不了.

4. 对于自然生成却失败的辅助线要有优化的意识

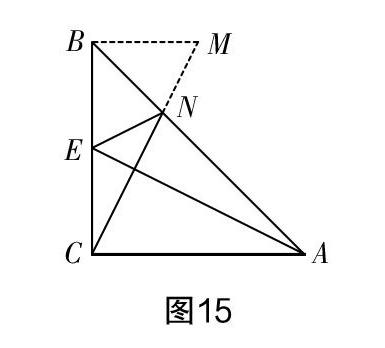
学生在实际的操作中，根据自身的知识构建出一条辅助线，却发现无法进行有效的推理，钻进一个胡同然后毫无头绪，可以另寻解决途径，然而结合已知条件将辅助线进行优化也不失为一条上策，用一个例题展示一下过程：如图14，在△ABC中，∠CAB=∠CBA=45°，CA=CB，点E为BC的中点，CN⊥AE交AB于N. 求证：AE=CN+EN.

一个学生的分析过程：看到这个结论是线段和差的形式，所以想到尝试用“补短”的方法来添加辅助线. 延长CN到点M，使得NM=EN，如图15，可是在接下来证明△BEN≌△BMN，△BCM≌△CAE都遇到了问题，没有办法得出任何一对三角形全等，从而整个证明停滞不前，接下来准备放弃这种方法.

从“截长”的角度添加辅助线，这个思路非常清晰到位，不过第一种辅助线就一定要舍弃吗？能不能通过再次分析题目的已知条件做个调整，△BCM与△CAE已经有一对边BC=AC，一对角∠BCM=∠CAE，所以在描述辅助线的时候可以换个角度，直接使得CM=AE，就可以补充这两个三角形全等所需的第三个条件，进而证明△BEN≌△BMN，进一步推理根据线段的等量代换完成整道题目的证明.

启示  本题通过改变对辅助线的描述将一条被放弃的辅助线“起死回生”，这对那些有这种经历的学生有莫大的鼓舞. 在这种思维方式的启发下，他们自己也很快找到了新的方法：过点B作AC的平行线交CA的延长性于点M或者过点B作BM⊥BC交CN的延长线于点M. 他们能这样举一反三，对笔者也是莫大的鼓舞.

几何证明问题对辅助线的添加一直都是一个教师关注的热点，也是一个老生常谈的话题，怎么把这首老歌唱出新意，也是笔者在教学的过程中一直思考的问题. 通过对已知条件的挖掘，结合想得到的证明结果，寻找这两者的连接点，如果之间的桥梁需要我们去搭建，就可以从实际需要出发，实现辅助线的有效生成. 以上的一些浅显的个人想法希望能够抛砖引玉，与同仁们一起探讨辅助线自然生成的生长点，为我们的实际教学注入新的想法.