中国共产党执政生态系统可靠性的计量分析
车 辚
(云南农业大学 马克思主义学院,云南 昆明 650201)
在系统工程学中,可靠性是指产品、系统在规定条件下和规定时间内完成规定功能的能力。可靠性在系统工程学中是一个重要技术指标,它与性能、成本、时间等技术经济指标同时作为评价系统好坏的标准。可靠性是一种综合性技术,达成目标需要如下几个步骤:(1)在设计阶段要分析系统或设备所具备的可靠性水平,应从成本、性能、政策、社会需要等各方面综合考虑来决定,然后确定可靠性目标。(2)在设计方案完成后要进行可靠性预测。(3)将预测推算结果与原定可靠性目标进行比较,作为以后修订方案的依据。(4)对组成系统的各子系统、单元进行可靠度分配。对于控制系统来说,可靠性问题不仅是故障问题还有故障后修复的能力问题。因此,与可靠性相对应的一个概念叫做维修性或修复性,是指系统发生故障后在规定条件下和规定时间内的修复能力。由于各种主客观因素的影响,系统出现故障很正常,但如果发生故障后能很快修复并维持一个良好的工作状态,这样的系统可靠性就比较好。把不发生故障的可靠性与排除故障的修复性两者相结合考虑,可称为广义的可靠性。
可以将可靠性的概念引入中国共产党执政生态系统的研究中。可靠性是指在一定的自然环境和社会环境条件下,系统保持正常运转和连续工作的能力,它关系到系统能否履行执政使命、实现执政目标,是系统内在结构安排、制度设计、资源组织在性能上的综合反映。可靠性工作贯穿系统的规划、设计、构建、演化、修复、校正、反馈各个环节,既需要对历史数据如故障发生时间、排除故障时间、故障发生频率、故障发生时的环境条件等进行收集和分析,寻找出影响系统可靠性的弱点;又要具有全局观,提前预判可靠性问题,恰当实施前馈设计、可靠度分配、冗余系统采用、元器件更新等措施,确保系统运转正常。能够对系统可靠性的相应能力作出数量表示的量,称为可靠性的特征量。其主要特征量有:可靠度、失效率、平均失效间隔时间、故障平均修复时间、维修度、有效度等。任何一个特征量只能表示可靠性的某一个特征方面,对于一个系统的可靠性评价需要综合使用各种特征量。
一、可靠度R(t)
可靠度是指产品、系统在规定条件下和规定时间内完成规定功能的概率。所谓规定条件就是指系统所处的环境条件、运转条件、维护条件等。所谓规定时间,根据具体情况可以是长期的若干年,短期的几个小时或一次性动作。所谓规定功能就是指系统应具有的经济技术——序参量指标。可靠度是一个定量指标,如果某类元器件、基本因子或系统工作24小时的可靠度为0.90,则如有20个这样的系统或因子,在规定的环境条件、运转条件、维护条件下工作24小时,平均有90%的系统或因子能保持各项经济技术——序参量指标处于正常的工作状态。可靠度以R(t)表示,则0≤R(t)≤1。一般而言,如果一个系统由若干个子系统或单元组成,其可靠性为各单元可靠度的乘积。系统越庞大、越复杂,所使用的元器件越多,则可靠性越差。假设一个系统每个元器件的可靠度均为0.99,如果有10个元器件组成系统,则该系统可靠度为0.90;如果是100个元器件组成系统,则该系统可靠度仅为0.37。[1]207
将可靠度的概念引入中国共产党执政生态系统的研究中,可以发现,新民主主义革命时期,中国共产党局部执政生态系统各子系统所处的环境条件差别很大,北方的黄土高原、太行山区、华北平原、长白山区与南方的河汊水网、大别山区、武夷山区等在自然地理、风土人情、文化习俗、社会结构等方面迥然不同,维持系统运转的经济条件、社会条件、政治条件等也有很大差异,系统遭遇封锁、围困、破坏后修复条件因党情、区情、敌情的不同而不同。例如,东北抗日联军1937年春鼎盛时整编为11个军,约4.5万人,抗日游击区扩大到70余县,从“九一八事变”至“七七事变”的6年时间共歼灭日伪军约14万人。但东北抗日联军是孤军作战,面对着30万日本关东军的重兵“围剿”,又经常活动在长白山和兴安岭的森林中,冰天雪地,极度缺乏给养,可以说系统的环境条件、运转条件、维护条件极其恶劣。这样的抗战一直坚持了14年,抗联的主要领导人杨靖宇(第一路军总司令)、赵尚志(第三军军长)、夏云杰(第六军军长)、陈荣久(第七军军长)等大部分牺牲,兵力损失过半。由于敌人采取“归屯并户”“十家连坐”的封锁政策,加上长白山区、完达山麓、小兴安岭地广人稀,部队补充兵员、给养极为困难,再加上抗联力量过于分散、内部缺乏核心领导,系统的修复一再受挫。以抗联所处的环境条件、运转条件、维护条件能够坚持14年抗战可以说体现了局部系统极高的可靠度。当然,除了不利因素外,抗联有一个其他子系统没有的地缘条件,就是活动区域靠近苏联,可以得到苏联的支持和援助。中共中央驻共产国际代表团从1935年开始直接领导东北工作,在1940年日本增兵东北后,采取保存实力、逐渐收缩的方针,各军缩编成10个支队分散活动。同年冬起,抗联部队相继转移到苏联边境进行整训。同时,他们经常派小部队回东北进行侦察、袭扰活动,指导和支援留在国内的部队打击日伪军。经过整训的东北抗日联军保持了一支有生力量,在1945年8月9日苏联军队大举进攻日本关东军时,他们在中苏边界营地召开反攻誓师大会,配合苏联红军作战,解放了一些城市和乡村,为战后中共军队抢占东北提供了有利条件。如果没有苏联的支持和援助,东北抗日联军的整训和修复是很难完成的,这就是局部系统的修复条件。修复条件越好,可靠度越高。
二、失效率(或故障率)λ(t)
失效率是指设备、系统工作t时刻后,单位时间内发生失效或故障的概率。失效是指系统丧失了规定的功能,对可修复的系统则失效也称为故障。失效过程大体分为三个阶段,如图1[1]210所示:
1.早期失效期
失效率随着时间由高值迅速下降,这是由于部分元件、因子或子系统因内部缺陷在系统正式投入运行初期造成的大量损坏,需要在调试期或运转早期予以排除的缘故(这也叫做可靠性筛选)。这个时期的主要任务是找出不可靠的原因,从而促使失效率下降并渐趋稳定。

图1
将失效的概念引入中国共产党执政生态系统的研究中,可以发现,在中国共产党成立初期也存在政治系统早期失效现象,除了牺牲和病逝使党的核心领导层发生大量减员外,脱党、开除党籍和叛党也造成政治系统不能正常发挥各种政治功能。尤其是大革命失败后,1927年至1937年是中国共产党和红军内部叛变行为最为猖獗的时期,上至党的总书记、政治局委员,下至各根据地、各红军中军、师、团级干部都有叛变投敌者。中央委员和候补中央委员中代表性的如向忠发、顾顺章、卢福坦、李竹声。在中央红军主力1934年开始长征后,留守根据地的党和红军将领面临空前严重的局面,一部分意志薄弱者选择叛变投敌如龚楚、陈洪时、曾洪易、刘士杰等人。这些红军将领虽不是中央委员,但却是各根据地、军分区主要负责人,他们的叛变直接造成局部执政生态子系统的失效。分析影响政治系统可靠性的因素有内因和外因,内因包括党自身的不成熟、党的力量弱小、党内路线斗争、领袖集团的不团结、领袖的牺牲、领袖政治态度的变化等因素,也跟结构设计缺陷、制度安排不当、人员素质达不到要求等因素有关。如红军第五次反“围剿”时,既有军事最高三人团,又有红军总司令部、总政治部、总参谋部等机构;领导人交叉任职普遍,既有军队职务,又有地方职务,还有派出机构职务;机构设置臃肿,职能混乱不清,权力边界模糊;共产国际不仅派出军事顾问执掌决策大权,还遥控指挥。这套指挥系统从一开始就陷入被动,上级的意图和下级的观念存在严重冲突,属于典型的早期失效。外因包括国内外形势的变化、共产国际和苏联的态度、反动派的疯狂镇压等,这属于系统运行的环境条件、运转条件、维护条件。
2.随机(偶然)失效期
这时期失效率趋向常数,它描述了系统正常工作状况下的可靠性。在这个期间所产生的失效可以认为是随机的和偶然的,相当于普阿松分布。此时期是系统的主要工作时期,时间较长,失效率最低而且稳定。
将随机失效概念引入中国共产党执政生态系统的研究中,随机失效是指系统在长期运行中,一些子系统由于领导人非程序性更迭、突发性事件、外部环境发生重大变化等因素退出工作状态。例如,顾顺章的叛变是新民主主义革命时期党中央面临的最严重突发事件,由于他曾是政治局委员,又长期负责特科工作,他对中央机关的情况和负责同志的情况,知道得非常清楚。加上中央领导同志常在他家里碰头,所以,连他的家属、亲戚以及佣人,都认识许多中央负责同志。事实上,在顾顺章叛变后,党中央负责同志已不能在上海立足,周恩来、博古、张闻天、陈云等人不得不先后进入中央根据地,导致一段时间中共中央的工作陷入停顿状态,这就是系统的随机失效。子系统的随机失效在“左”倾冒险主义、关门主义在党内占统治地位时是一个大概率事件。例如,从1931年初到1932年底,中共河北省委遭到三次大的破坏,唐山市委、北平市委、直中特委也遭到破坏,白区赤色工会会员到1932年1月剩下不过3000人,由于缺少掩护,临时中央机关也难以在上海立足,不得不于1933年1月迁入中央根据地。[2]333中共临时中央迁入根据地后,党在上海成立了中央局,作为临时中央的派出机关,领导党在国民党统治区的工作,并负责和共产国际联系,这是一种修复性的举措。但是,上海局继续执行“左”倾冒险主义方针,只存在了两年零七个月。从1934年3月到1935年2月,它遭到六次大的破坏。中共河北省委于1933年又遭到四次破坏。北平市委从1933年5月到1935年5月,遭到四次破坏。1934年9月,由于中央局的电台被破坏,中国共产党被迫中断和共产国际的无线电联系。1935年2月,由于叛徒出卖,上海局及其在上海的下属机关几乎被国民党特务机关全部破坏。7月,上海局不再存在。至此,白区党的组织,除少数地方党部外,绝大多数均遭破坏。[2]333-334
新中国成立后,20世纪50年代末开始至70年代末,党内“左”倾错误一直占据主导地位,中国共产党执政生态系统各子系统在这个期间随机失效也是一个大概率事件。例如,“文革”初期由于刘少奇、邓小平被打倒,中央书记处实际上就陷入停滞,由中央文革小组取而代之,这也属于系统的随机失效。随后的“红卫兵”全面夺权运动导致中央和地方的许多党政领导干部受到批斗,机关工作普遍陷于瘫痪、半瘫痪状态,党的基层组织的活动和党员的组织生活都陷于停顿。西方学者估计,文革期间在1500万至2000万的行政干部中清洗率达20%之多,在大区和省级达到70%—80%,在中央一级达到60%—70%。他们还统计,“其政治地位未受文化大革命影响的,23名政治局成员中只有9人,13名书记处成员中只有4人,167名中央委员会成员中只有54人。15位副总理和48位部长中,只有一半左右在运动末期仍留在国务院内”。[3]231,232随机失效具有偶然性、突发性,难以预计什么时候发生,但在“文革”中却是一个大概率事件。在一定阶段,随机失效的失效率近似为一常数,记为λ,即它能连续工作到时间t的概率。
3.损耗失效期
损耗失效是指系统在长期运行中,一些子系统由于历史使命完成或者不能适应形势发展的需要退出工作状态,在这一时期内失效率又迅速上升。如新中国成立初期的中央各大区地方局,东北局、西北局、西南局、中南局、华东局等在历史使命完成后撤销,就属于系统的损耗失效,但这属于主动损耗失效。还有被动损耗失效,这是由于元器件、因子或子系统老化衰退所致,大部分因子丧失性能。如中央红军开始长征时,有一、三、五、八、九共五个军团8.6万余人,经过湘江血战只剩3万余人,八军团所剩无几撤销建制。扎西会议后中央红军进行了整编,全军缩编为16个团,其中一军团2个师6个团、三军团4个团、五军团3个团、九军团3个团,这就是局部系统的被动损耗失效。如果能预先知道元器件和因子开始损耗的时间,提前进行更换,就可以把上升的失效率拉下来,延长系统的有效寿命。
三、平均失效间隔时间(MTBF)
这是指设备或系统在两相邻故障间隔内正确工作时的平均时间。如第1次工作t1时间后出现故障,第2次工作t2时间后出现故障,第n次工作tn时间后出现故障,则平均失效间隔时间MTBF= ∑ ti/n(i=1,2,3,…,n)。
MTBF常用来描述设备和系统的可靠性,对于中国共产党执政生态系统而言,在新民主主义革命时期,大部分时间由于敌人的强大和各子系统被分割包围,一旦不能打破敌人的“围剿”系统就会出现失效。利用MTBF的概念可以对各根据地、方面军、子系统进行可靠性描述。以红四方面军为例,从1927年11月的黄麻起义开始计算,至1932年10月鄂豫皖苏区反第四次“围剿”失败,中央分局和方面军总部率主力2万余人越平汉路向西转移,子系统第1次有效运转时间t1=5年(59个月)。1932年12月,红四方面军进入陕南、川北,解放通江、南江、巴中,创立川陕根据地,相继粉碎敌人的“三路围攻”“六路围攻”,又进行了多次进攻战役,部队发展到5个军11个师32个团总计8万余人。1935年3月,红四方面军为策应中央红军的行动发起“强渡嘉陵江”战役,进入川康地区,这就等于放弃川陕根据地。尽管是主动放弃,但却具有被动原因:由于长期战争的消耗、破坏和执行“左”的政策,使川陕苏区到了民穷财尽的地步,已无法支持大规模的反“围剿”斗争。为了摆脱困境和打破敌人正在准备的“川陕会剿”,西北革命军事委员会决定采取“依托老区,发展新区,向甘南发展”的方针。红四方面军在收缩战线的过程中,根据张国焘的指示,不适当地实行“坚壁清野”,给人民财产造成了损失;不适当地把地方武装集中起来编为4个独立师全部带走,给以后根据地坚持斗争带来困难。因此,这次撤退可以理解为是一次局部系统的失效,子系统第2次有效运转时间t2=2年3月(27个月)。第3次失效发生在红一、四方面军在草地会师后,1935年8月,张国焘擅自率军南下,经过艰苦作战遭遇重大损失,部队减员一半,不得不从进攻转为防御,而且东进、南下均不可能,部队无法获得兵源、给养、武器的补充,处境极为被动。子系统第3次有效运转时间t3=5月。这样,我们可以计算出以红四方面军为核心构建的局部子系统平均失效间隔时间 MTBF=(59+27+5)÷3=30.3(单位:月)。
四、平均故障修复时间(MTTR)
这是指设备和系统出现故障后到恢复正常工作时所需要的时间。如第1次故障修复的时间为Δt1,第2次故障修复的时间为Δt2,第n次故障修复的时间为 Δtn,则 MTTR= ∑ Δti/n(i=1,2,3,…,n)。
MTTR也是用来描述设备和系统可靠性的关键指标,尤其是对于中国共产党局部执政生态系统和子系统的决策层,由于敌人的进攻或者破坏,常常导致领导集体的重大损失或根据地大面积丧失,从损失到重建的时间就是故障修复时间MTTR。例如,1941年1月6日—13日的“皖南事变”导致新四军军部及直属部队重大损失,军长叶挺被无理扣押,政治部主任袁国平牺牲,副军长项英、参谋长周子昆突围后不幸被叛徒杀害。可以说,新四军和东南局主要领导损失过半,陈毅、张云逸、邓子恢等人因在敌后幸免于难。但是,这时的中国共产党已不是1927年“四一二”政变时的政党,它已经变得成熟和强大,拥有50万军队和16块抗日根据地,所辖人口超过1亿,已经建立起一个大规模的、复杂的耗散结构系统,具有很高的稳定性和可靠性。“皖南事变”过去仅仅7天,中共中央军委于1941年1月20日发布重建新四军军部的命令,任命陈毅为代理军长,张云逸为副军长,刘少奇为政治委员,赖传珠为参谋长,邓子恢为政治部主任。1月28日,新四军新军部在苏北盐城成立,随即将全军整编为7个师和1个独立旅,共9万余人,继续坚持长江南北的抗战。新四军军部从损失到重建的时间就是故障修复时间MTTR只有15天。
又如,1942年4月华北日军对冀南根据地进行“四二九大扫荡”之后,根据地面积缩小到五分之三,平原抗战力量遭到很大损失。党组织近半数遭到破坏,党员人数由四万人减少到二万一千人。不少县、区的抗日政府,根本解体了。陷于敌人强力控制下的村政权已变成“两面政权”,资助了敌人。正规军减少了一半,剩下一万余人,游击队十之八九已经溃散。武器损失甚重,步枪损失约五千支。党政军民、区级连级以上的干部损失达四千至五千人。[4]138这样的损失可以理解为局部系统的失效或半失效。但从6月下旬开始,冀南地区很快地进行了重建工作。基本方针是:在武装斗争支持下,或以武装斗争为核心,把军事斗争与政治斗争、合法工作与非合法工作互相结合起来,建立起能够打击敌人的任何进攻、保护抗日力量的体制。由于方针正确、措施有力,冀南地区春季的混乱状态在6、7月间即已停止,8、9月间扭转了危局,10月以后扩大了游击区,在游击区及敌占区内建立了小据点,逐渐缩小了敌方占领地区。[4]267在以后一年的战斗中,使日军死伤四千余人,打死、打伤和俘虏伪军七千余人,缴获步枪五千余支,机枪五十余挺,完全弥补了春季作战中的损失。[4]266从这组数据看,冀南根据地故障修复时间MTTR只有6个月。
五、可靠性的运算式
可靠度R(t)、失效率(或故障率)λ(t)、平均失效间隔时间(MTBF)、平均故障修复时间(MTTR)都是系统可靠性的最主要特征量。与失效相对应的概念就称为可靠度R(t),一般是按负指数律分布的,即 R(t)=e-λt=e-t/D。如图 2[1]213所示 :
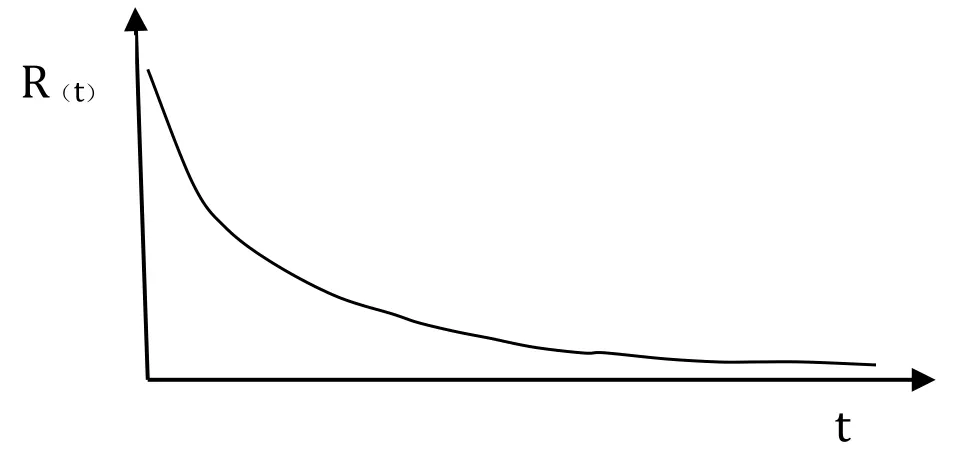
图2
其中λ是失效率,即在单位时间内失效的瞬时概率;D为其平均失效间隔时间,在时间Δt内出现失效的概率将为λΔt或Δt/D。至于其不能连续运转到时间t的概率,称为失效度,以Rˉ(t)表示,则有 Rˉ(t)=1-e-λt=1-e-t/D。[1]213
因此,以可靠度R(t)来衡量系统的可靠性,子系统i的可靠度为Ri(t),则失效度Rˉi(t)=1-Ri(t)。在并联结构中,只有当各个子系统都失效时,系统方失效。各子系统的故障相互独立时,系统失效的概率为各子系统失效概率的乘积,即系统的失效率 Rˉ(t)=Rˉ1(t)×Rˉ2(t)×Rˉ3(t)×Rˉ4(t)×Rˉ5(t)×Rˉ6(t)=[1-R1(t)]×[1-R2(t)]×[1-R3(t)]×[1-R4(t)]×[1-R5(t)]×[1-R6(t)]。而系统的可靠度,即R(t)=1-Rˉ(t)。当各个子系统的可靠度按负指数律分布时,R(t)=1-[1-e-λ1t]×[1-e-λ2t]×[1-e-λ3t]×[1-e-λ4t]×[1-e-λ5t]×[1-e-λ6t],λi为各个子系统的失效率。在串联结构中,任何一个子系统失效都将导致整个系统失效。系统的可靠度为各个子系统可靠度的乘积,即R(t)=R1(t)×R2(t)×R3(t)×R4(t)×R5(t)×R6(t)=e-λ1t×e-λ2t×e-λ3t×e-λ4t×e-λ5t×e-λ6t。[5]10-30这 样 的计算模式是假设每个子系统的失效率并未由于冗余配置而改变。实际上,在有些情况下,由于系统的演化,系统的结构和内部关系变得关联更强、关联更多,系统可能在内部生长出不同的层次来,每个子系统负担的压力和工作任务减轻,其失效率也随之下降。如延安时期中央成立的社会部,负责情报、反特、组织甄别、中央安全保卫等工作,就分担了参谋部、组织部、卫戍机关的一部分职能。
考察系统的可靠性问题,是确定一个系统在规定运行时间内没有失效的概率,即确定系统运行的时间长度t。前面我们计算出以红四方面军为核心构建的局部子系统平均失效间隔时间D≈30月,若系统一次连续运转时间t=30月,则可靠度R(t)=e-λt=e-t/D=e-30/30=e-1=36.8%(e=2.71828183)。因此,要得到较高的可靠度,D必须是运转时间的许多倍。例如,要得到R(t)=90%,则通过计算可知D=10t;如 R(t)=99%,则 D=100t。但当 D大于 t一定倍数以后,随着D的增加,R(t)的增加就比较缓慢。如图3[1]213所示,即为可靠度R与D/t的关系。

图3
当然,我们也可以用系统连续运转时间,即首次出现故障而使系统运转中断或者出现重大事件的时间之期望值来表示其可靠性。这时可以用系统在长期运行中的平均利用率来表示系统可靠性。如果系统平均连续运转时间为T,中断后平均修复时间为τ,则在系统运转过程中没有出现降级使用等使系统功能有所改变的情况下,系统利用率η=T÷(T+τ)。[5]35以新四军为例,从1937年10月12日新四军成立起,直到1941年1月6日“皖南事变”发生,系统连续运转1179天,故障修复时间为15天,系统利用率η=T÷(T+τ)=1179÷(1179+15)=98.7%。系统可靠性的计算本身是一个问题,往往不一定要求很精确。况且系统遇到的问题并不一定都是随机的,其失效率也不一定是常数。即使系统出现故障,故障的修复概率也不一定是随机的,而是有记忆性、经验性的,是可以人为地加以干涉的。
六、元素和子系统的可靠度分配
可靠度分配就是根据系统的可靠度目标,合理地调配各子系统的可靠度指标。它是系统可靠性设计的重要环节,其目的在于落实系统的可靠性目标,确定子系统的可靠度指标。可靠度分配的基础是可靠性预测。实际上,一个合理的可靠性设计往往需要经过多次预测、分配,再预测、再分配的循环才能实现。分配原则是:一般对于容易实现高可靠度的子系统提出高的要求,对于不易实现高可靠度的子系统则提出低的要求,在满足可靠度目标条件下应使整个系统的运转成本、维护成本尽可能最小。可靠度分配的具体方法有等分配法、加权分配法和动态规划最优分配法等。由于社会生态系统的复杂性、规模性,内部存在强烈的非线性相互作用,运用加权分配法和动态规划最优分配法都十分困难,等分配法简单直接,可以说清楚问题所在,因此,本文采用等分配法描述中国共产党执政生态系统的可靠度分配。
在有n个子系统的串联系统中,要求每个子系统都分配以相等的可靠度。在串联结构中,系统的可靠度为各个子系统可靠度的乘积,即R(t)=R1(t)×R2(t)×R3(t)×R4(t)×R5(t)×R6(t)=e-λ1t×e-λ2t×e-λ3t×e-λ4t×e-λ5t×e-λ6t。设定 Rs 为串联系统的可靠度目标,Ri为第i子系统的可靠度指标,则有 Rs= ∏ Ri(i=1,2,3,…,n)。按照等分配要求,则可得出Ri=Rs1/n。[1]229-230
例:假设一个系统由4个子系统组成,设定该系统的可靠度目标是0.656,按照等分配法,每个子系统的可靠度指标Ri=0.6561/4=0.9。
新民主主义革命时期,白区工作中的可靠度分配就是采用这样的等分配法,情报工作和统战工作不能交叉,各子系统之间不发生横向联系,单线纵向联系一般交通员只知道上线和下线的联系方式,甚至不知道具体人,只是通过中介传递信息和情报。系统的可靠度为各个子系统可靠度的乘积,一旦某个子系统失效(叛变),就会极大降低整个系统的可靠度,甚至导致子系统的解散或崩溃(如顾顺章叛变就是这样的例子)。军队系统由于政治性、组织性、纪律性、统一性的要求,也呈现出串联结构特点,也可以采用等分配法分配可靠度。从上述的例子可看出,即使每个子系统分配的可靠度指标达到0.9,串联的结果整个系统的可靠度目标只有0.656。如果我们按照前面计算的新四军的可靠度目标0.987(利用率),根据军、师、团、营四个层级单位等分配可靠度,则每个子系统的可靠度指标Ri=0.9871/4=0.997。
等分配法主要运用于串联结构,这在中国共产党局部执政和全国范围内执政时都存在。在革命战争年代和抗日战争时期,执政系统的组成部分较为精干,人员少,环节少,层级少,呈扁平式结构,党的执政意图可以快速通过军事系统、政治系统、地方行政系统传递和实现。西方学者评论说:“中共控制区内的政治权力是通过一种党、政、军、民的连锁结构而在各个层次上发生作用的。这些机构在陕甘宁边区得到最充分的发展,在它们之上是中央机关和八路军总部。这些组织就其效率而言,远比日占区和民主中国的组织要高。”[6]753全国胜利后,由于我们在相当一段时期实行高度集中的计划经济体制,党委和政府掌握着几乎所有的资源配置权力,执政机构庞大,执政生态系统中子系统众多,人员多,环节多,层级多,呈金字塔式结构。纵向看,中央、省(区、市)、市(州)、县(旗)、乡(镇、街道)五级结构组成执政系统,有明显的串联特征,适用等分配法分配可靠度。如果设定大系统的可靠度目标为0.9,则每个子系统的可靠度指标Ri=0.91/5。具体运算如下:两边取对数,㏒10Ri=㏒100.91/5=0.2× ㏒100.9=0.2×(-0.0458)=-0.00916,Ri=0.979。换言之,每级系统的可靠度必须达到0.979,才能实现大系统的可靠度目标0.9。

