协变量缺失下变系数部分非线性 模型的统计推断

杜海燕 王连国 王秀丽

( 1)山东师范大学数学与统计学院，250358，济南； 2)济南市龙奥学校，250000，济南 )

1 引 言

本文考虑变系数部分非线性模型，其一般形式为

Y=XTα(U)+g(Z,β)+ε，

(1)

其中X∈Rq,Z∈Rr,U∈R,g(·,·)是已知的非线性函数，β=(β1,…,βp)T为未知的参数向量，α(·)=(α1(·),…,αq(·))T是未知的q-维系数函数，ε为模型误差且满足E(ε|X,Z,U)=0，Var(ε|X,Z,U)=σ2,X,Z及U为协变量，Y为响应变量.关于模型(1)的统计推断，已经有部分学者对其进行了研究，Li和Mei[1]最先提出了该模型的统计推断问题，他们主要采用了非线性最小二乘方法对参数部分和非参数部分进行了估计. Zhou 、Zhao和Wang[2]研究了变系数部分非线性模型的经验似然统计推断，构造了参数和非参函数的置信域. 模型(1)具有良好的灵活性，它包含了多种模型，比如，当g(Z,β)=0时,该模型就是变系数模型，该模型的讨论在Fan和Zhang[3]的文章中可见. 当g(Z,β)=ZTβ时，该模型就变成了常见的变系数部分线性模型. 若X=1和q=1，模型(1) 就成为Li和Nie[4]研究的部分非线性模型. 若模型(1) 中不存在协变量X,U,则模型就是非线性模型，Bates 和Watts[5]对其进行了研究.

在实际应用中，我们往往不能获得全部的观测数据，经常遇到数据缺失的情形，处理该情形的常用方法有: 完全数据分析法，逆概率加权法，似然方法等.在协变量缺失下情形下，Liang[6]研究了协变量缺失时的半参数广义部分线性模型，将局部线性回归与局部拟似然方法和加权估计方程相结合，估计了参数分量和非参数分量.Liang和Qin[7]运用经验似然的方法对部分线性模型中的参数分量和非参数分量进行估计，并得到了相关的渐近性质. Chen、Feng和Xue[8]基于逆概率加权最小二乘方法研究了协变量缺失数据下半参数变系数部分线性模型的估计问题. 本文基于逆概率加权最小二乘方法，考虑了协变量Z缺失下变系数部分非线性模型的统计推断.

2 估计方法

设{(Yi,Xi,Zi,Ui),i=1,…,n}是来自以下变系数部分非线性模型的独立同分布观测样本

Yi=XiTα(Ui)+g(Zi,β)+εi,i=1,2,3,…,n,

(2)

其中(Yi,Xi,Ui)可以完全观测，协变量Zi随机缺失.引入示性变量δi，当δi=1时，Zi可观测，当δi=0时，Zi缺失.进一步假定Zi为随机缺失(MAR),详细介绍可参考文献[9]，即

P(δi=1|Yi,Ui,Xi,Zi)=P(δi=1|Yi,Ui,Xi)=π(Yi,Ui,Xi).

(3)

(3)式中暗含在给定Yi,Ui和Xi的条件下，δi和Zi是独立的.

在实际应用中，π(Yi,Ui,Xi)往往是未知的，通常使用logistic回归模型作为缺失机制，即

Yi-g(Zi,β)=XiTα(Ui)+εi,i=1,2,…,n.

(4)

首先，对αj(u)在任意给定u0的某个小邻域内泰勒展开

其中a=(a1,…,aq)T，b=(b1,b2,…,bq)T.对给定的β，由于协变量Z缺失，利用逆概率加权的思想，关于aj和bj极小化(5)式

(5)

可得aj和bj的估计，其中Kh(·)=K(·/h)/h,K(·)是核函数，h为带宽. 为表示方便，引入记号：

Y=(Y1,…,Yn)T,g(Z,β)=(g(Z1,β),…,g(Zn,β))T,ε=(ε1,…,εn)T,

M=(X1Tα(U1),…,XnTα(Un))T,W(u0)=diag(Kh(U1-u0),…,Kh(Un-u0)),

(6)

从而可得α(u)的估计为

(7)

其中Iq和0q分别为恒等矩阵和零矩阵，从而M的估计可以表示为

(8)

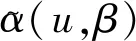
(9)

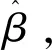
(10)

3 估计的渐近性质

下面提出以下假设：

C1 U有有界支撑Ω，它的密度函数f(u)是Lipschitz连续的，且在Ω上有f(·)>0.

C2 {αj(u),j=1,…,q}关于u有连续的二阶导数.

C3 对任意的Z,g(Z,β)是关于β的连续函数，且关于β有连续的二阶导数.

C4 存在某个s>2，使得E(‖X‖2s)<且E(‖g′(z,β)‖2s)<，且存在某个ε<2-s-1，使得当n→时，n2ε-1h→.

C5 矩阵E[g′(z,β)⊗2]和E[E(g′(z,β)|U)⊗2]在β的邻域内有界.

C6 核函数K(·)在有界支撑内是对称密度函数，带宽h满足nh8→0和nh2/(logn)2→.

C7 对任意U∈Ω,Γ(U)q×q为正定矩阵，且矩阵Γ(U),Γ-1(U)和Φ(U)均为Lipschitz连续的.

C8π(·)在(Yi,Ui,Xi)的支撑下与0是有界的，并且有连续的二阶偏导数.

定理1假设条件C1-C8成立，若β为真值参数向量，则

定理2假设条件C1-C8成立，对任意u∈Ω有

4 主要结果的证明

4.1预备引理

引理1[11]假设(X1,Y1),…,(Xn,Yn)是n个独立同分布的随机向量，其中Yi是一维随机变量，若进一步假设E|Y1|s<且，其中f(·,·)表示(X,Y)的联合密度函数，令K(·)表示满足Lipschitz条件且有有界支撑的有界正函数，那么给定某个ε<1-s-1使得n2ε-1h→时，有

(11)

引理2令g′(z,β)=(g′(z1,β),g′(z2,β),…,g′(zn,β))T,假设条件C1-C8成立，那么我们有

(12)

(13)

其中Σ1=E[g′(z,β)g′(z,β)T]-E[ΦT(U)Γ-1(U)Φ(U)],Δ=diag(δ1/π1,…,δn/πn),

证简单计算可得

利用期望的平滑性及引理1易得

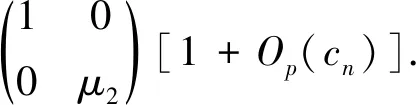
(14)

类似的，我们同样可求得

X(u)TW(u)Δg′(z,β)=nf(u)Γ(u)⊗(1,0)T[1+Op(cn)].

(15)

由(14)、(15)可得

(XT0)[X(u)TW(u)ΔX(u)]-1X(u)TW(u)Δg′(z,β)=XTΓ(u)-1Φ(u)(1+Op(cn)).

(16)

由假设条件C3、C5及大数定理可得

类似于等式(16)的推导，我们得到

(XT0)[X(u)TW(u)ΔX(u)]-1X(u)TW(u)ΔM=XTα(u)(1+Op(cn))，

(17)

因为E(ε|X,U)=0,结合(12)式有

(XT0)[X(u)TW(u)ΔX(u)]-1X(u)TW(u)Δε=XTΓ(u)-1E(X|U=u)Op(cn).

在假设条件都成立的情况下，我们可以推出

=ξn+E[g′(z,β)-Φ(U)TΓ(U)-1X][1+op(1)]Op(cn)

(18)

其中A=E(τ1τ1Tπ1(1-π1)).

引理4假设条件C1-C8都成立，那么我们有

(19)

引理5假设条件C1-C8成立，那么我们有

(20)

4.2定理的证明

(21)

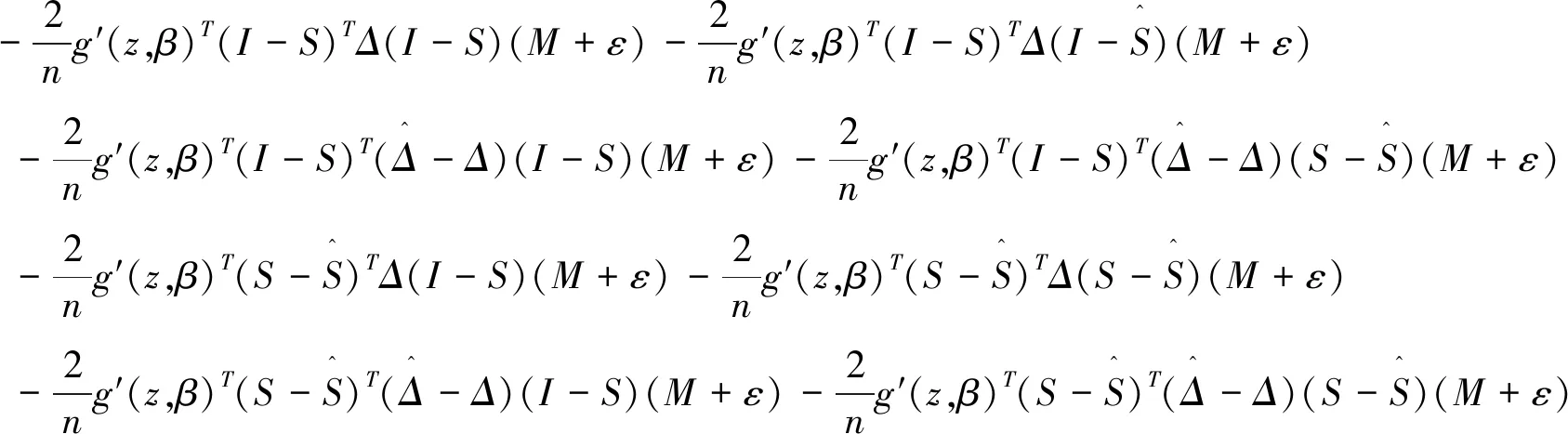
=：R1+R2+R3+R4+R5+R6+R7+R8.

(22)

且

通过(12)可得

tTQ″(β*)t=2n{tTΣ1t+Op(||t||3)}.

(23)

定理2的证明经计算可得

=：s1+s2+s3+s4.