浮置板剪力铰对列车-轨道耦合系统动力学行为的影响

杨建近， 朱胜阳， 翟婉明

(西南交通大学 牵引动力国家重点实验室，成都 610031)

城市轨道交通因其运量大、速度快、能耗低、安全准时、绿色环保等特点，已成为城市交通出行的重要方式，特别是我国已经进入了城市轨道交通急速、全面发展的新时期[1]。然而城市轨道交通在方便人们出行的同时，也带了一些亟待解决的问题，如其引起的环境振动问题，钢弹簧浮置板轨道因其具有优良的隔振性能被广泛应用于环境振动敏感区段[2]。由于浮置板是不连续的，轨道结构的刚度在两相邻浮置板板端位置(板端接缝位置)就会降低，列车通过时就会产生参数激扰[3]，振动沿轨道纵向传播时板端的动力响应甚至会被放大[4]。若两相邻浮置板板端位置不采取接缝措施，会降低轨道的整体连续性，一方面会导致轨道的参振质量减小，另一方面也会使相邻浮置板在轮对通过时产生较大的板端位移差，恶化轮轨相互作用关系，加剧列车-轨道耦合系统的振动响应。因此，工程上常在相邻浮置板间安装剪力铰装置，以提高轨道的整体连续性，降低上述不利影响。

浮置板轨道中的剪力铰一般为锰钢制件，从力学角度来说其只传递剪力而不传递弯矩、纵向水平力。从构造上可认为是一种梁结构。吴磊[5]分别用梁模型和剪切弹簧模拟剪力铰，发现两种模型模拟的结果具有很好的一致性，其研究结果表明剪力铰的刚度越大，剪力铰的作用越明显，板端扣件力幅值越小。姚纯洁等[6]建立了浮置板轨道静力学分析有限元模型，分析垂向车辆静荷载作用下钢弹簧浮置板系统的静位移，发现剪力铰能够有效地限制浮置板过大的竖向变形。蒋崇达等[7]通过耦合相邻板间剪力铰栓接处的竖向自由度来模拟剪力铰的约束，但这种考虑方式与剪力铰对浮置板的实际约束作用差别较大，只适合定性模拟剪力铰对浮置板板端变形的限制效果。蒋吉清等[8]用Timshenko梁模拟钢轨和浮置板，用弯剪弹簧阻尼模拟剪力铰，建立1/4车辆和轨道垂向耦合动力学模型，通过分析多种工况下系统动力学响应，得到了剪力铰的最优参数取值。Hussein等[9]用Euler梁模拟浮置板，用竖向剪切弹簧模拟剪力铰，建立垂向的轨道动力学模型，利用周期结构法分析了移动简谐荷载作用下剪力铰竖向刚度对轨道结构振动的影响。徐庆元等[10]用梁模型模拟钢轨、浮置板和隧道结构，用垂向大刚度弹簧模拟板端连接，通过分析不同板长、不同橡胶垫刚度组合工况下浮置板间纵向连接对系统动力特性的影响，得到了地铁隧道橡胶浮置板轨道需要纵向连接的条件。

从以往的研究可以发现，现有的浮置板剪力铰的理论模型多为竖向剪切弹簧模型，在分析浮置板剪力铰对系统动力学特性的影响时也多将浮置板和钢轨用梁模型模拟，因此大多局限于分析剪力铰参数对系统垂向动力学的影响。而实际上，浮置板的实际构型更接近于板结构，剪力铰对浮置板不仅有竖向约束作用还有横向约束作用。本文采用弹性薄板模型模拟浮置板，运用横向和竖向剪切弹簧模拟剪力铰，建立了剪力铰连接条件下车辆-浮置板轨道空间耦合动力学模型，不仅分析了剪力铰对列车-轨道耦合系统垂向振动的影响，也分析了列车通过曲线时剪力铰对系统横向振动的影响。

1 动力学分析模型

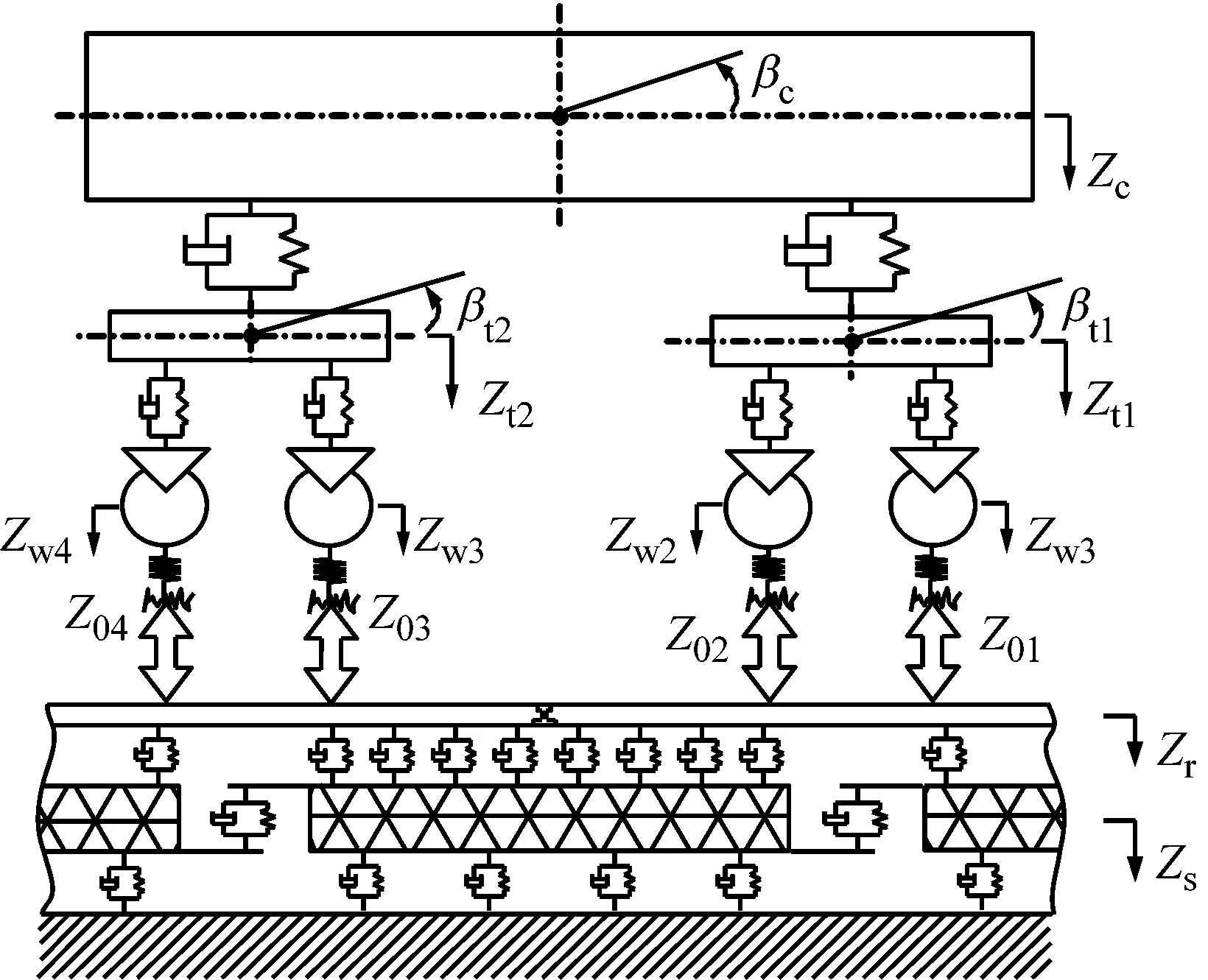
基于车辆-轨道耦合动力学理论[11]，考虑浮置板剪力铰对浮置板横向和竖向的约束作用，建立了剪力铰连接条件下列车-钢弹簧浮置板轨道空间耦合动力学模型。其中，列车模型由多节车辆编组而成，每辆车辆视为35自由度多刚体系统(见表1)，扣件系统和钢弹簧装置用弹簧阻尼单元模拟，浮置板剪力铰用竖向和横向剪切弹簧模拟；车辆-浮置板轨道耦合动力学模型，如图1所示，剪力铰对浮置板的横向约束作用，如图2所示。

(a) 主视图

(b) 端视图

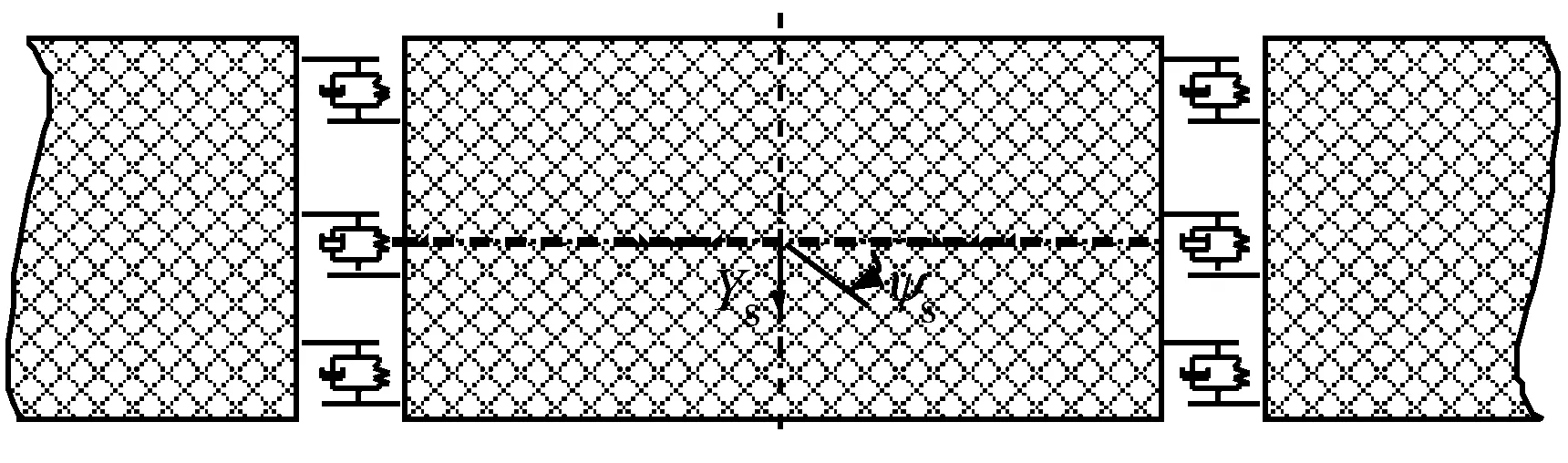
图2 剪力铰对浮置板横向约束示意图

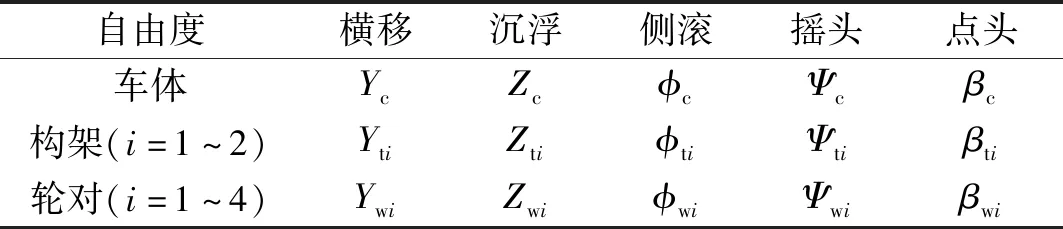
自由度横移沉浮侧滚摇头点头车体YcZcϕcΨcβc构架(i=1～2)YtiZtiϕtiΨtiβti轮对(i=1～4)YwiZwiϕwiΨwiβwi

根据文献[11]，每辆车辆的动力学方程可以写成如下形式

(1)

式中：Zv为车辆的位移向量；Mv、Cv和Kv分别为35×35阶车辆的质量矩阵、阻尼矩阵和刚度矩阵；Fv为车辆系统受到的荷载向量，由车辆系统受到的重力和轮轨相互作用荷载组成。

钢轨竖向振动微分方程为

(2)

横向振动微分方程为

(3)

扭转振动微分方程为

(4)

式中：Yr、Zr和φr为钢轨的横向、垂向和扭转位移；Iry和Irz分别为钢轨截面对横轴和竖轴的转动惯量，Ir0为钢轨截面的极惯性矩；Er为钢轨的弹性模量，GKr为钢轨抗扭刚度；ρr为钢轨密度；mr为每延米钢轨的质量；Pm、Qm和Mwm为第m个轮对施加到钢轨上的垂向力、横向力和扭转力矩；xwm为第m个轮对在钢轨上的纵向位置；Nw为列车的轮对数量；FVpn、FLpn和Mpn为第n个轨下支撑对钢轨的垂向支反力、横向支反力和支反力矩；xpn为第n个扣件在钢轨下的纵向位置；Np为一根钢轨下扣件个数。

考虑剪力铰对浮置板的作用，第k块浮置板的垂向振动微分方程为

(5)

横向振动方程为

(6)

绕竖向中心轴转动方程为

(7)

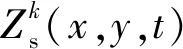
扣件和钢弹簧的支反力与其受压缩量成正比，具体的求解表达式见文献[11]。第k块浮置板上第m个剪力铰施加给浮置板的荷载求解表达式为

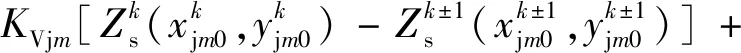
(8)

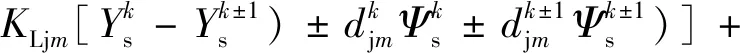
(9)

式中：当剪力铰位于第k块和k+1块浮置板之间时取上面的符号，当剪力铰位于第k-1块和k块浮置板之间时取下面的符号；KVjm和CVjm为第m个剪力铰的垂向剪切刚度和阻尼；KLjm和CLjm为第m个剪力铰的横向剪切刚度和阻尼。

采用Ritz法，引入钢轨竖向振动、横向振动和扭转振动的正则阵型，可将式(2)～式(4)变换为二阶常微分方程，采用双向梁函数组合级数逼近法将浮置板的垂向振动振型表示为浮置板长度、宽度方向的梁振型函数的组合[12]，将式(5)也变换为二阶常微分方程。从而剪力铰连接条件下钢弹簧浮置板轨道的振动方程变换为下形式

(10)

式中：ZT为轨道结构的广义位移向量；MT、CT和KT分别为轨道系统的广义质量矩阵、广义阻尼矩阵和广义刚度矩阵；FT为轨道系统受到的广义荷载向量，由轮轨相互作用乘以钢轨的各阶振型函数组成。

在式(1)和式(10)中，都需要求解轮轨相互作用力，其中轮轨法向力采用Hertz非线性弹性接触接触理论，轮轨切向力采用经典的蠕滑理论求解。如此，车辆和轨道结构的振动方程通过轮轨相互作用关系彼此相互影响，耦合成一个大型复杂非线性动力学微分方程。对于如此大型复杂的非线性动力学微分方程，采用文献[13]提出的Zhai方法进行快速数值积分求解，其积分格式为

(11)

式中：Δt为时间积分步长；下标n为t=nΔt瞬时；φ和φ为积分控制参数，一般均取为0.5即可达到稳定条件。

2 模型对比及验证

为了验证所建模型的正确性，利用Fortran语言对上述建立的动力学模型进行编程计算，并与实测结果进行对比。实测数据为西南交通大学列车与线路研究所在深圳地铁1号线测得，测试区间为直线段浮置板轨道，钢轨为CN60钢轨，轨道结构的主要参数见表2。运行的列车由6辆地铁A型车(4M2T)编组而成，车速为75 km/h。

根据实测线路的轨道状况，计算中采用与实际线路不平顺条件较为接近的美国AAR6级轨道谱(波长范围1～80 m)和短波不平顺谱(波长范围0.05～1 m)作为外部激励。图3为本文模型计算得到的钢轨、浮置板垂向加速度与实测结果的对比，同时给出了垂向耦合动力学模型(浮置板采用Euler梁模型)的计算结果，图中负值表示方向竖直向上。由图3可知，本文模型计算得到的钢轨、浮置板垂向振动加速度的总体趋势和数值大小与实测结果吻合良好，验证了所建立模型的正确性。同时，由图3(b)可知，浮置板采用两种模型计算得到的浮置板振动加速度差异较为明显，钢轨振动加速度也有一定的差异。由于采用弹性薄板模型更符合浮置板的实际结构，得到的结果与实测结果更为接近。需要指出的是，垂向动力学模型不能分析列车和轨道的横向振动，即不能分析剪力铰对列车-轨道耦合系统横向振动的影响。

表2 轨道结构的主要动力学参数[14]

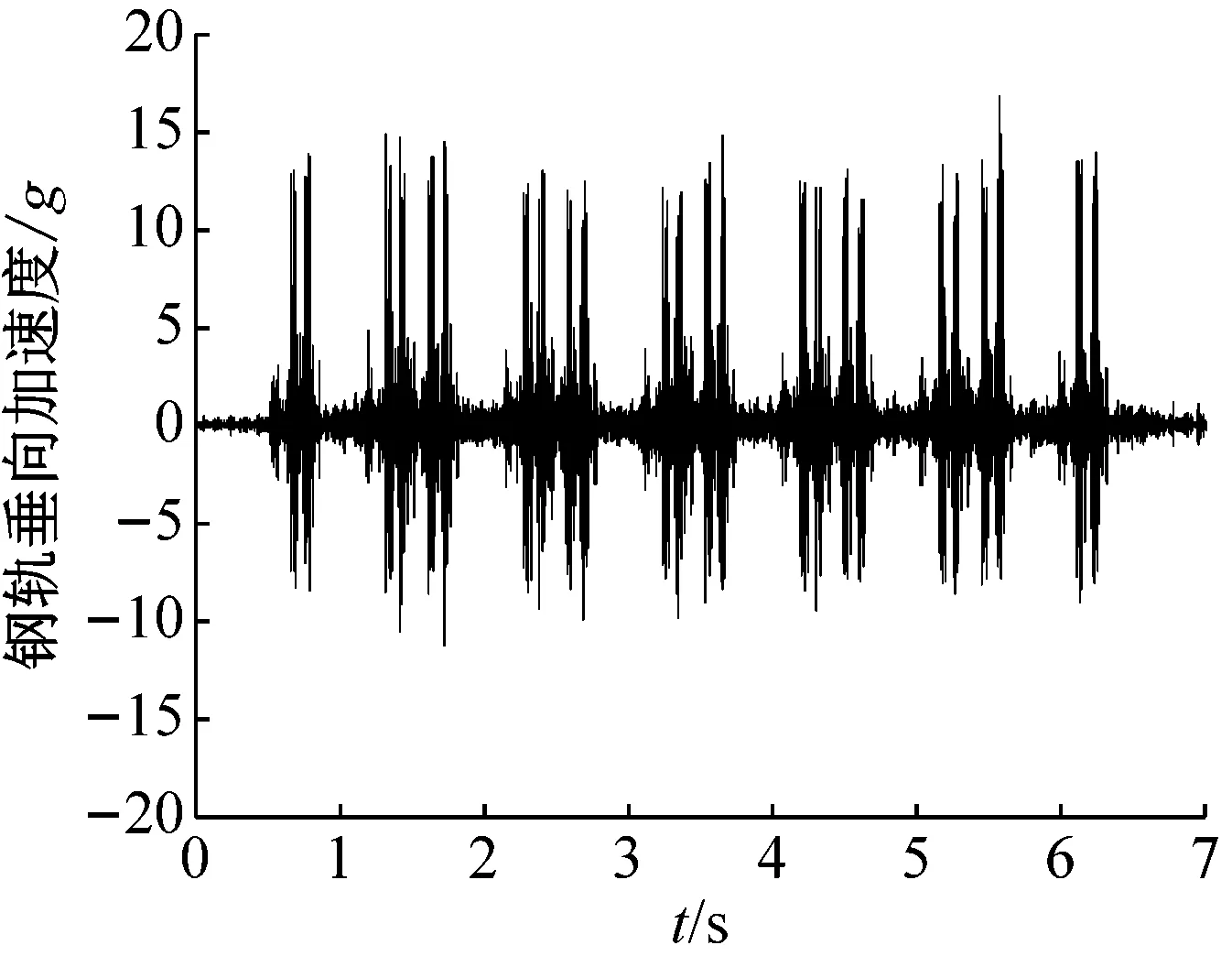
(a) 实测结果

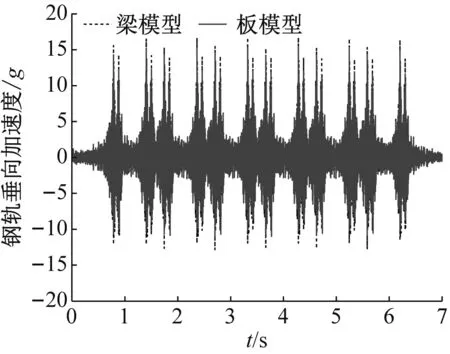
3 浮置板剪力铰对轮轨系统动力学行为的影响

为了探明浮置板间安装剪力铰装置对列车-轨道耦合系统动力学行为的影响，利用上述建立的空间耦合动力学模型，分析列车通过直线段和曲线段浮置板轨道时系统的动力学响应。轨道的动力学参数与表2中的一致，列车运行速度为80 km/h。分析中为了排除其他因素的干扰，不考虑轨道不平顺的影响。

3.1 直线段浮置板轨道

取第1位轮对右侧轮轨相互作用为研究对象，分析浮置板间安装剪力铰装置对轮轨相互作用的影响。图4是有无剪力铰时第1位轮对通过浮置板时轮轨垂向力、横向力及对应的轮载下的钢轨垂向位移。图中竖虚线表示浮置板接缝中心位置。

由图4可知，无论是否安装剪力铰装置，由于浮置板的不连续，随着轮对在浮置板轨道上移动，轮轨力、轮载下钢轨位移和轮对垂向位移都呈现出周期性变化的规律。轮对位置距离浮置板接缝位置越近，剪力铰的存在对轮轨相互作用的影响越大。

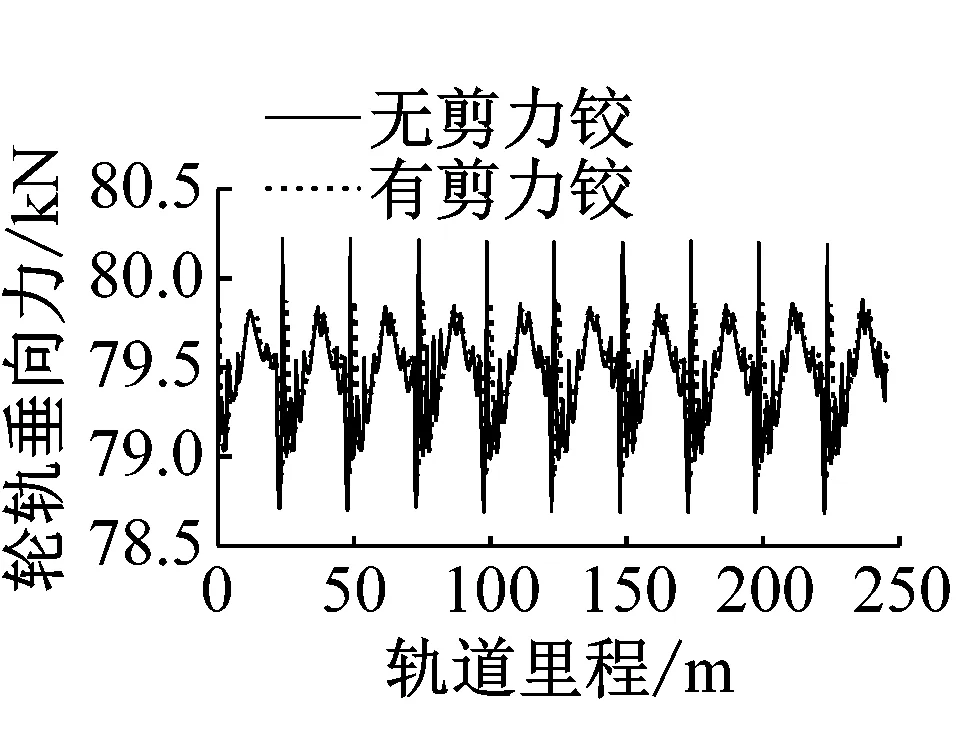
(a) 1位轮对右侧轮轨垂向力

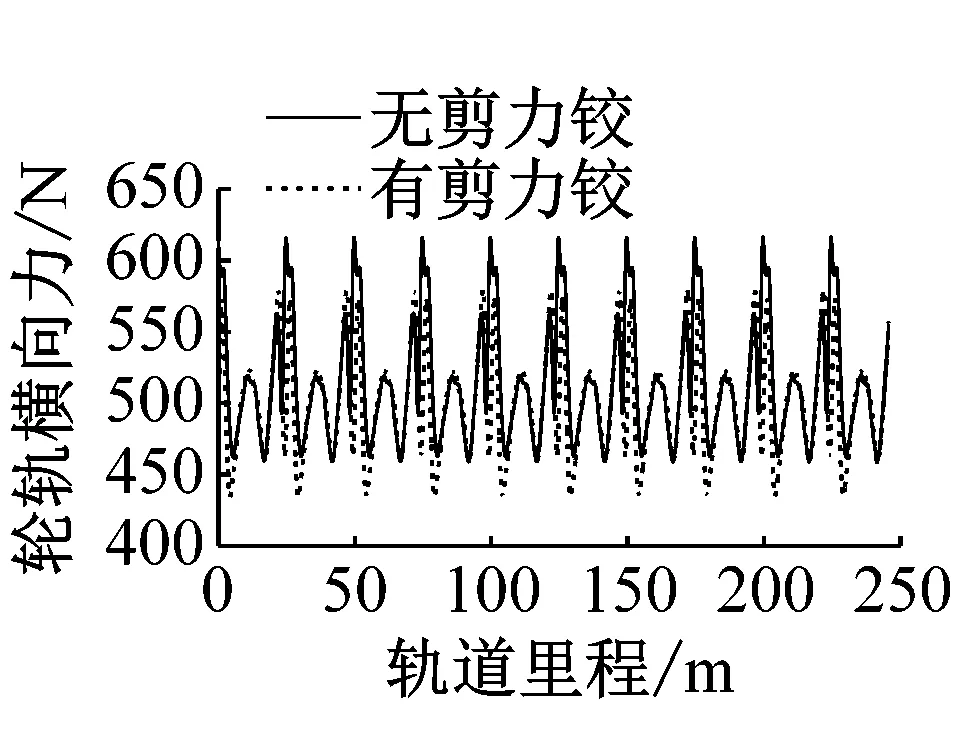
(b) 1位轮对右侧轮轨横向力

图4 直线段浮置板剪力铰对轮轨相互作用的影响

Fig.4 Influence of hear hinges on wheel/rail interaction with straight track

由图4(a)和图4(b)可知，在浮置板间无剪力铰装置时，轮对通过浮置板接缝位置时，垂向轮轨力产生了明显的冲击，并在轮对通过浮置板接缝后，垂向轮轨力的震荡现象比较明显。而安装剪力铰装置后，垂向轮轨力的震荡现象减弱，特别是轮对通过浮置板接缝位置时，轮轨垂向力突变明显减弱，轮轨横向力也有所减小。由图4(c)和图4(d)可知，轮对的垂向位移对钢轨的垂向位移有很高的跟随性，剪力铰装置对钢轨和轮对的垂向位移的影响几乎一致。浮置板安装剪力铰装置后，轮对通过浮置板接缝位置时，轮载下钢轨垂向位移明显减小。

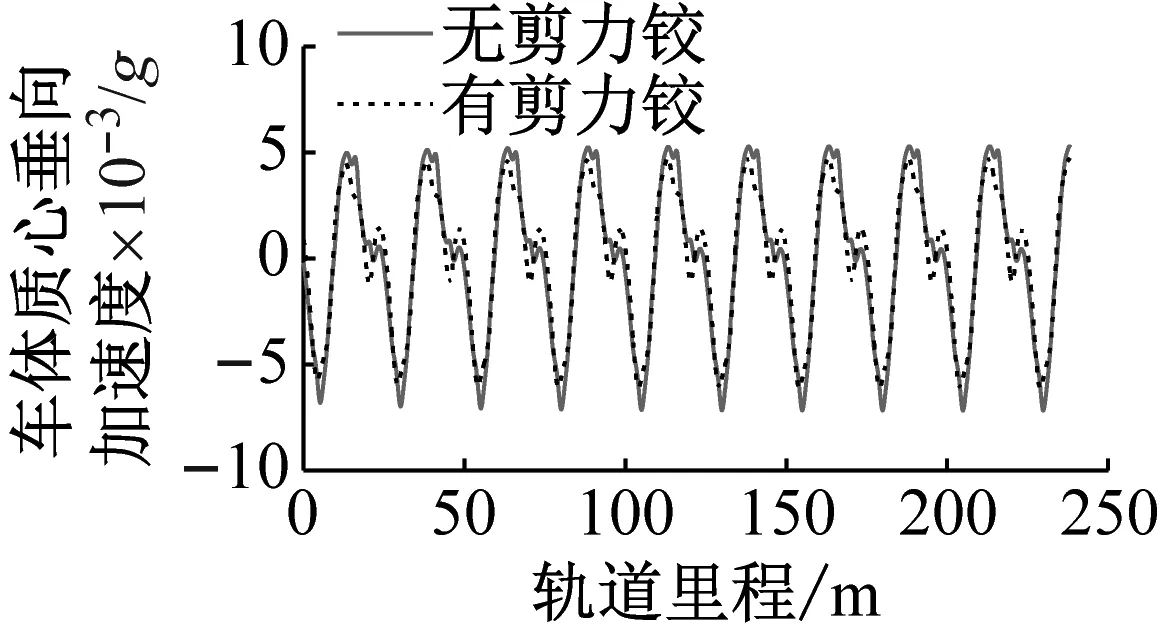
图5为有无剪力铰时头车的车体质心、第1位端转向架质心和第1位轮对质心的垂向加速度时程曲线，正方向竖直向下，负值表示加速度方向向上。

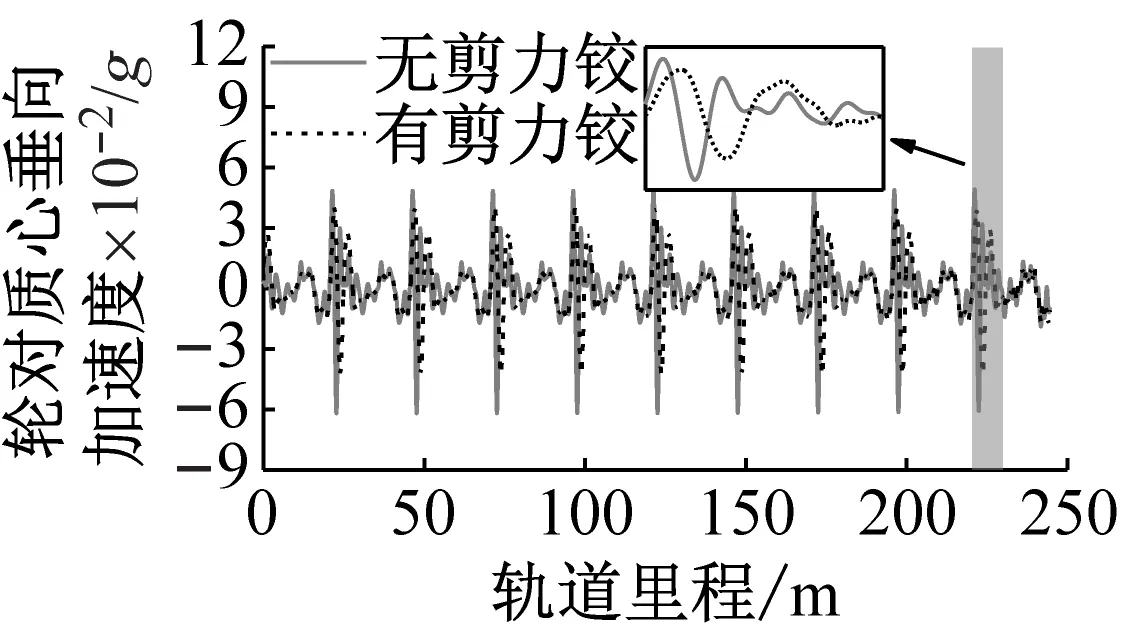
(a) 轮对质心垂向加速度

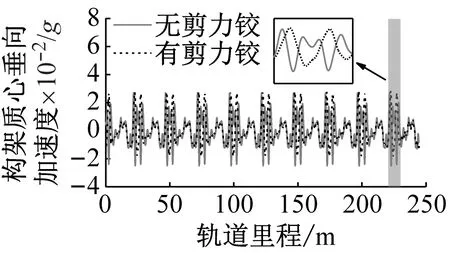
(b) 构架质心垂向加速度

(c) 车体质心垂向加速度

图5 直线段浮置板剪力铰对车辆振动的影响

Fig.5 Influence of hear hinges on vehicle vibration with straight track

由图5可知，无论是否安装剪力铰装置，由于浮置板的不连续，车辆各部件的振动也呈现出周期性变化的规律，而且经过一系和二系悬挂系统的衰减，从轮对到构架再到车体的振动幅值逐渐减小，振动的频率成分也越来越少。浮置板剪力铰装置对轮对的垂向振动影响最大，对构架的垂向振动影响次之，对车体的垂向振动影响最小。

由图5(a)可知，无论是否安装剪力铰装置，轮对通过浮置板接缝位置时，轮对质心垂向加速度均产生了明显的跳变。在浮置板间无剪力铰装置时，轮对质心垂向加速度先急剧增大到最大值0.048g，然后又急剧减小到最小值-0.062g，变化幅值约为0.1g。从局部细节图可进一步发现，轮对通过浮置板接缝前后，其垂向加速度呈现两个连续“M”形波动。而在安装剪力铰装置后，轮对质心垂向加速度的最大峰峰值为0.82g，减小了18%，同时轮对通过浮置板接缝前后，其垂向加速度波动变为了一个“M”形。

由图5(b)和图5(c)可知，浮置板剪力铰装置对转向架垂向振动加速度的影响与轮对有类似的规律，而对车体振动行为的影响较小。

取浮置板中部和端部以及靠近中部截面处的扣件、钢弹簧为研究对象，分析浮置板间安装剪力铰装置对列车动荷载作用下轨道结构振动的影响。图6为有无剪力铰时浮置板轨道上各部件的动力学响应。其中扣件弹性恢复力和钢弹簧支撑力的正值代表其受压，负值代表其受拉。

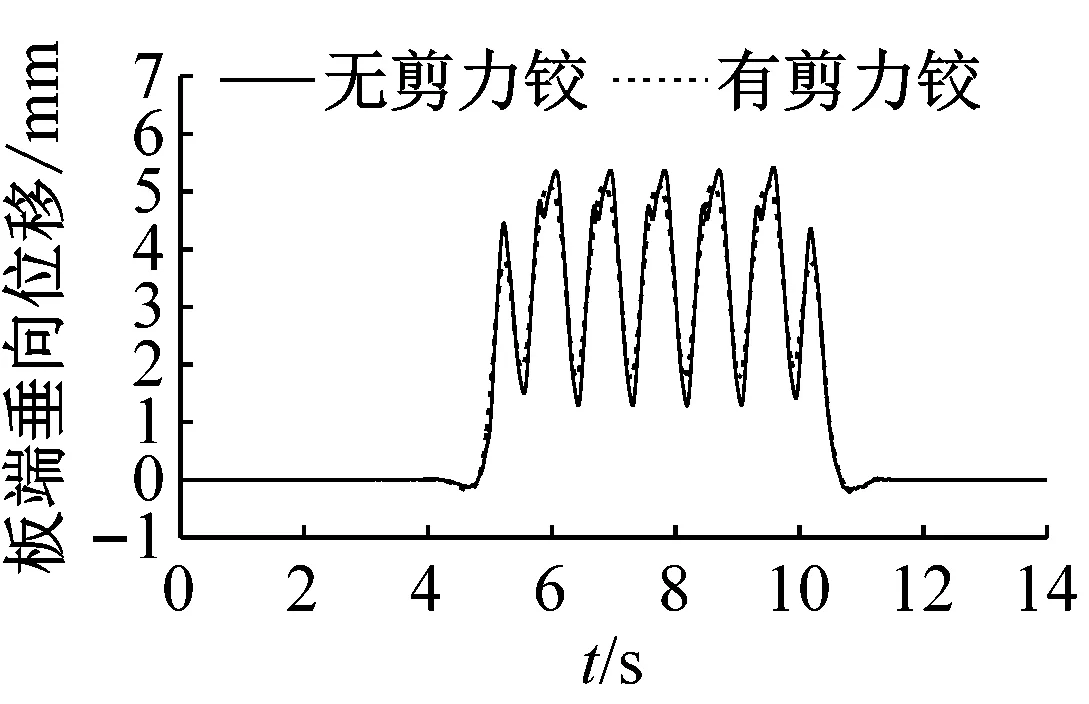
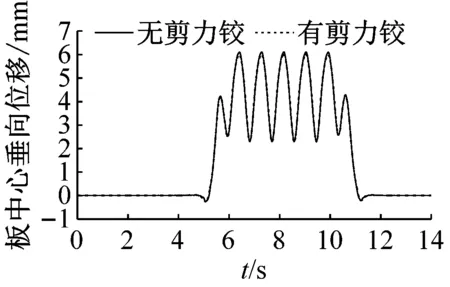
(a) 浮置板垂向位移

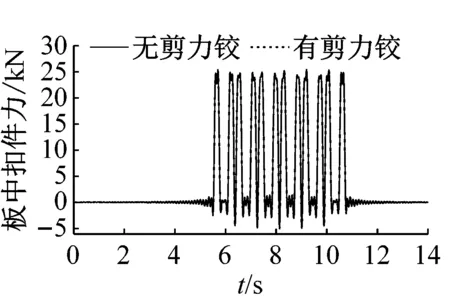
(b) 扣件弹性恢复力

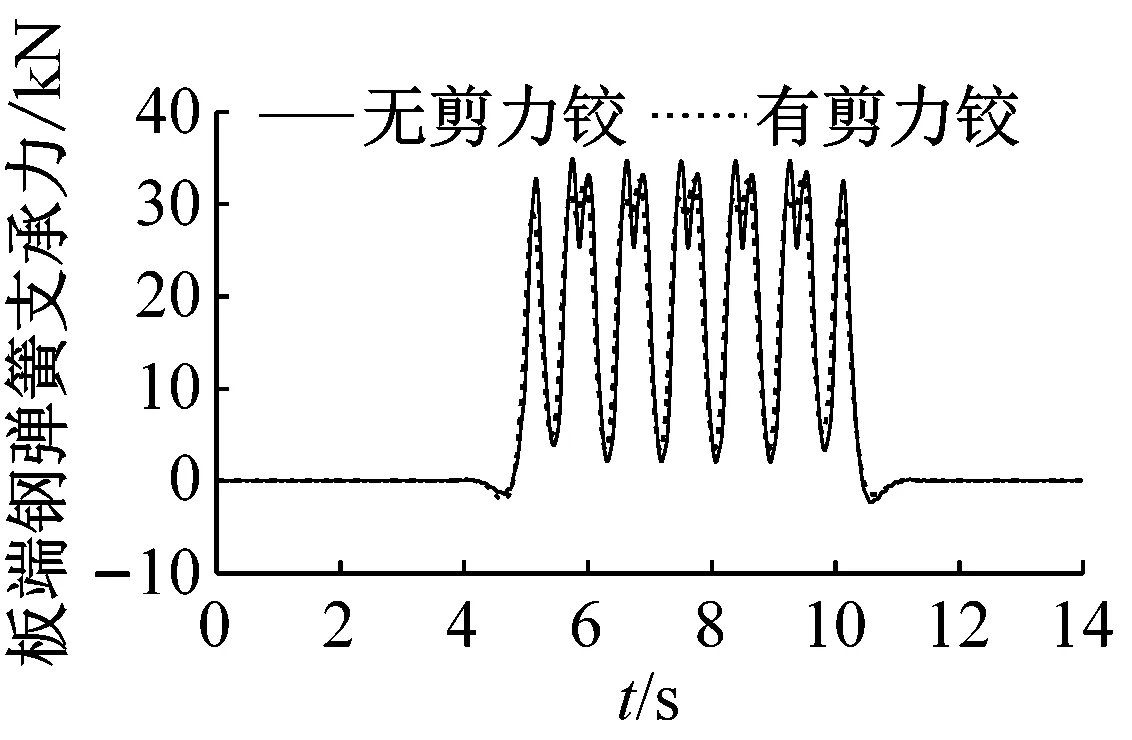
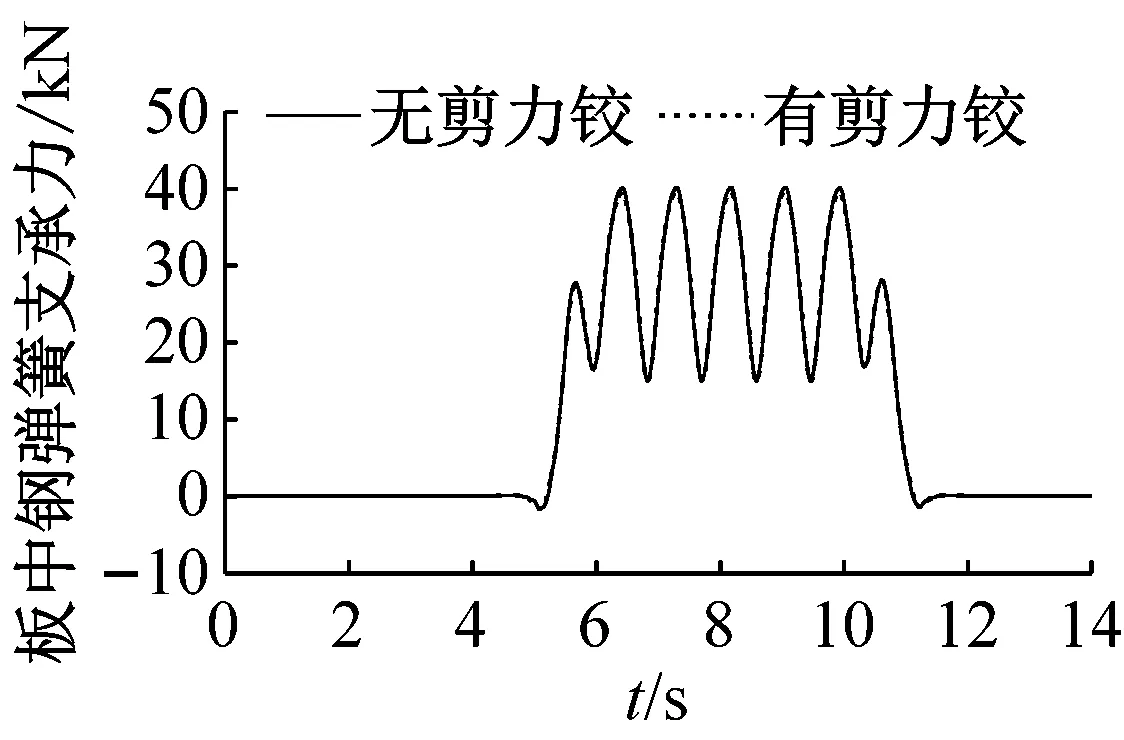
(c) 钢弹簧支承力

图6 直线段浮置板剪力铰对轨道横向动力学响应的影响

Fig.6 Influence of hear hinges on dynamic behaviors of the track with straight track

由图6可知，剪力铰装置仅对浮置板接缝位置近处的轨道结构的振动产生明显的影响，特别是板端处的扣件力；而对远离接缝位置的轨道结构振动几乎不受影响。未安装剪力铰装置时，板端扣件受到大幅值的拉伸力和压缩力的循环作用，最大压缩力为41.8 kN，最大拉伸力为21.9 kN，最大变化幅值达到62.7 kN，对扣件使用寿命非常不利。安装剪力铰装置后，最大压缩力为24.8 kN，减少了40.7%；最大拉伸力为2.6 kN，降低了88.1%；最大变化幅值为27.1 kN，减少了56.8%，板端扣件受力的状态明显改善，扣件使用寿命可得到延长。

3.2 曲线段浮置板轨道

根据《地铁设计规范》：GB 50157—2013，设定一段曲线线路浮置板轨道，线路曲线半径为1 000 m，缓和曲线长度为85 m，外轨超高为120 mm，浮置板轨道的主要动力学参数与表2中一致，列车通过速度为80 km/h。利用本文建立的动力学模型计算重点分析剪力铰对列车-轨道耦合系统横向动力学行为的影响。

图7为有无剪力铰条件下第1位轮对内侧的轮轨垂向力、横向力及相应轮载下的钢轨垂向位移。图中竖虚线表示浮置板接缝中心位置。

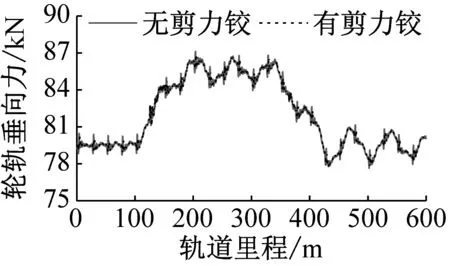
(a) 1位轮对内侧轮轨垂向力

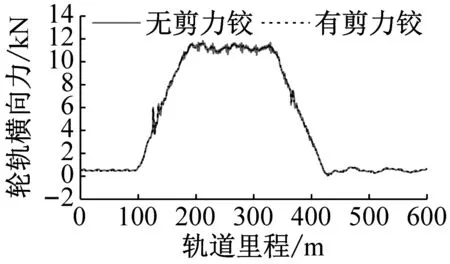
(b) 1位轮对内侧轮轨横向力

(c) 1位轮对内侧轮载下钢轨横向位移

图7 曲线段浮置板剪力铰对轮轨相互作用的影响

Fig.7 Influence of hear hinges on wheel/rail interaction with curve track

由图7可知，曲线轨道工况下，轮轨力、轮载下钢轨位移和轮对垂向位移均呈现出周期性变化的规律。轮对位置距离浮置板接缝位置越近，剪力铰的存在对轮轨相互作用的影响越大。无论是直线段还是曲线段，浮置板间无剪力铰装置时，轮轨垂向力和横向力都产生了明显的冲击，钢轨横向位移也急剧增大。而安装剪力铰装置后，列车通过曲线段浮置板轨道时轮载下钢轨横向位移明显减小，轮轨垂向力和横向力的波动范围也有所缩小。

图8为有无剪力铰时头车的车体质心、第1位端转向架质心和第1位轮对质心的横向加速度时程曲线。由图8可知，轮对在进入缓和曲段和出曲线段时，车辆系统各部件都会产生明显的冲击横向加速度；车辆运行于缓和曲段线路时，车辆横向振动最为恶劣。

浮置板安装剪力铰装置对轮对的横向振动影响最大，对构架的横向振动影响次之，对车体的横向振动影响最小。列车运行在曲线段线路上时，无剪力铰装置条件下轮对和构架的横向振动较为明显；轮对通过浮置板接缝时，轮对和构架的横向振动加速度会明显变大。当浮置板安装剪力铰装置后，轮对和构架的横向振动明显减小。

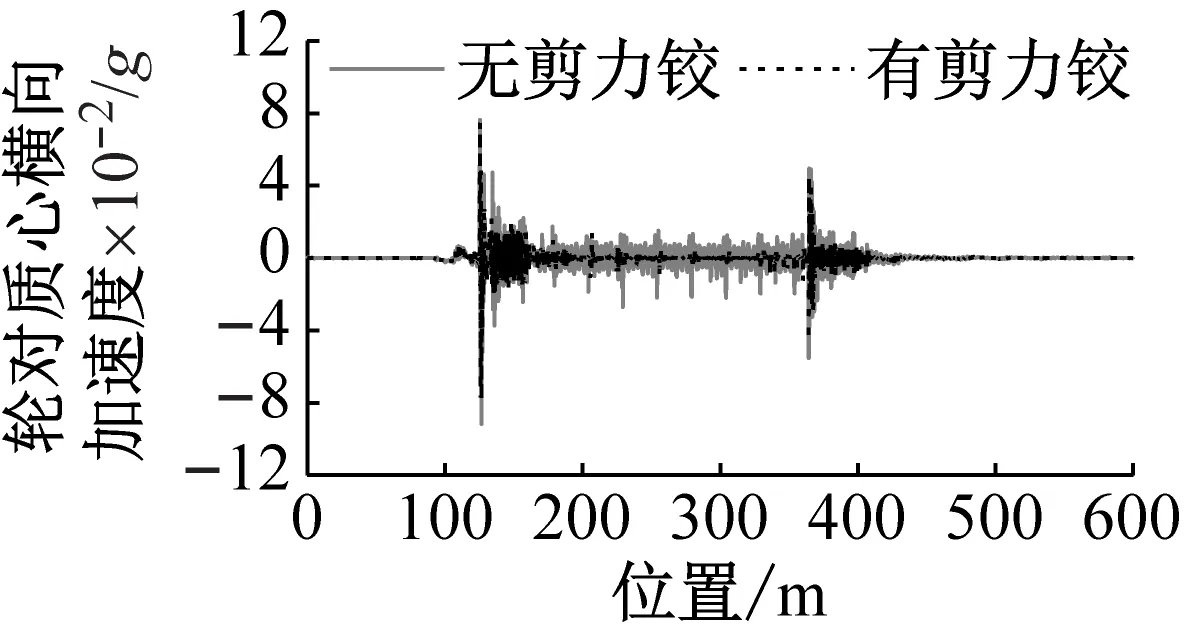
(a) 轮对质心横向加速度

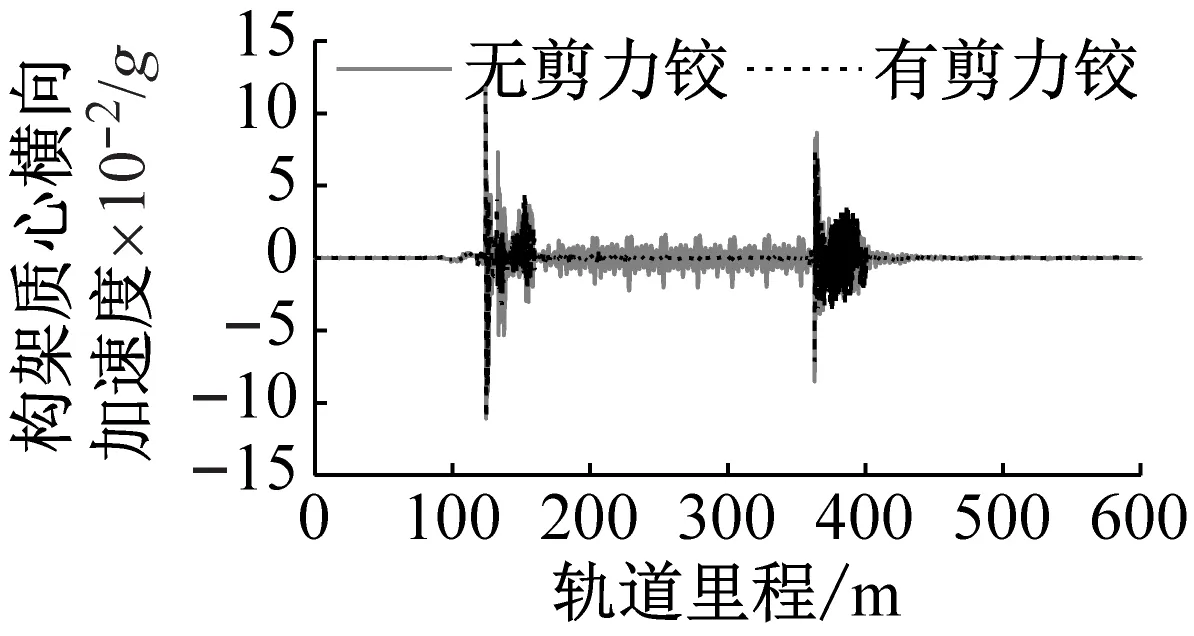
(b) 构架质心横向加速度

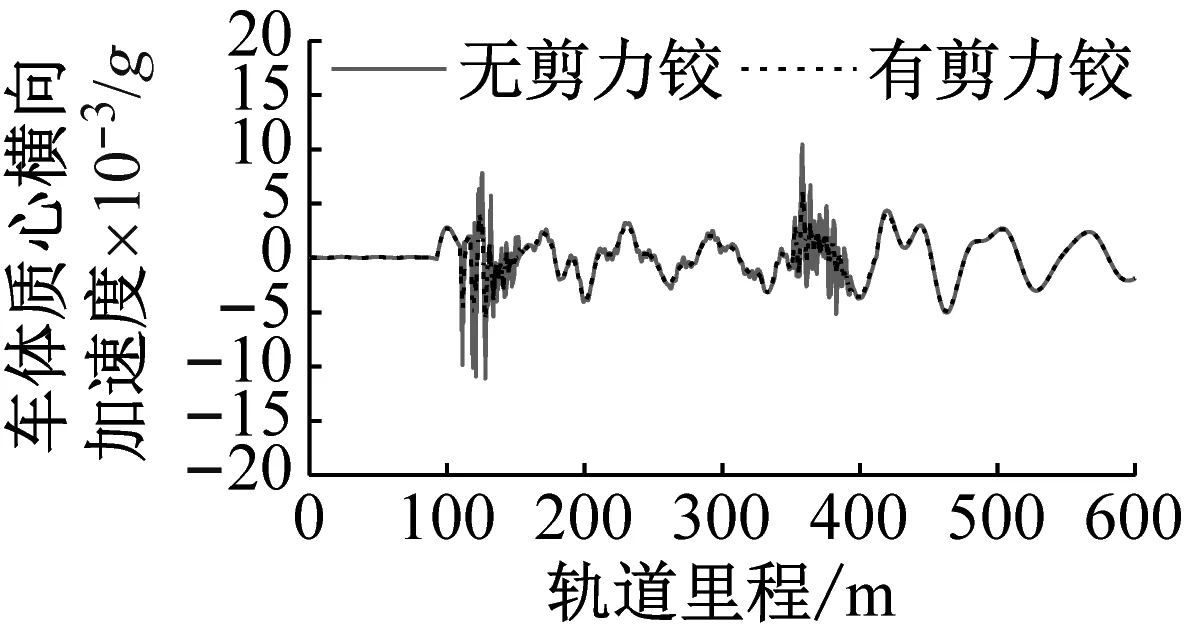
(c) 车体质心横向加速度

图8 曲线段浮置板剪力铰对车辆振动的影响

Fig.8 Influence of hear hinges on vehicle vibration with curve track

取位于曲线段中间位置的浮置板及其端部和中部截面处的扣件、钢弹簧为研究对象，分析剪力铰装置对列车荷载作用下轨道结构横向动力学行为的影响。图9为有无剪力铰时浮置板轨道上各部件的横向动力学响应。

由图9可知，无剪力铰的浮置板横向位移、水平面内转动角、板端钢弹簧横向力和板中钢弹簧横向力都会产生明显的波动，最大变化幅值分别为0.18 mm、2.8×10-5rad、1.02 kN和0.86 kN。安装剪力铰后，三者的波动明显减小，最大幅值分别减小为0.02 mm、3.0×10-6rad、0.22 kN和0.09 kN。由于浮置板钢弹簧对浮置板有横向约束作用，无论是有无剪力铰装置，浮置板横向位移和水平面内转角都较小， 对扣件横向力影响较小。

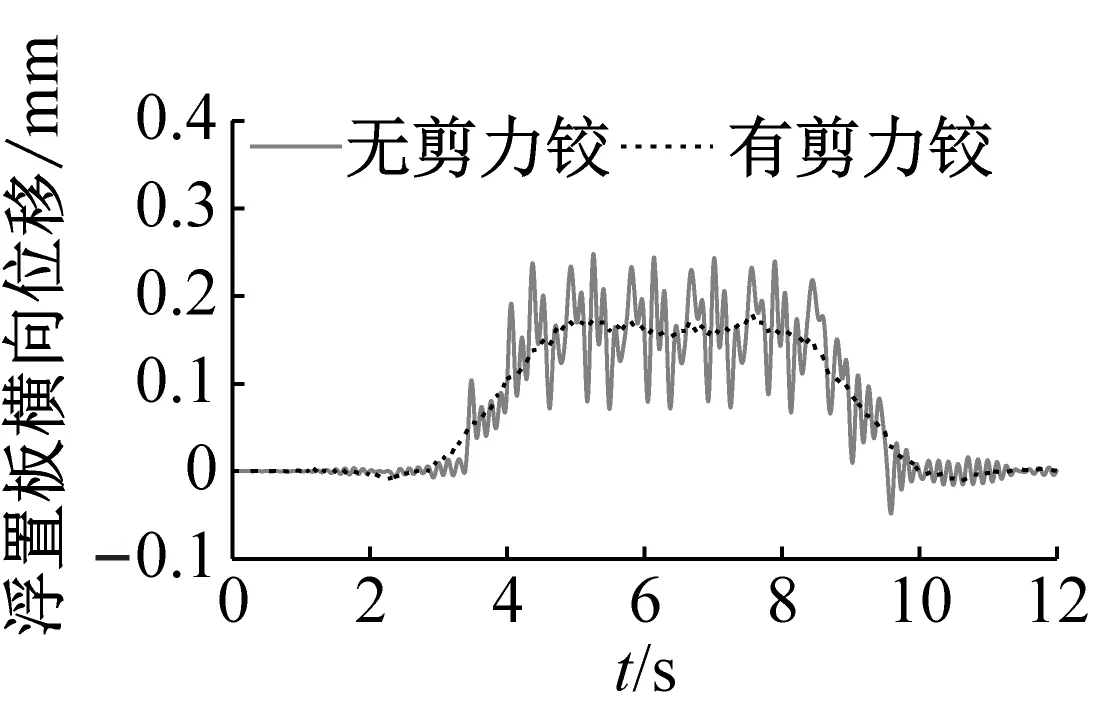
(a) 浮置板横向位移

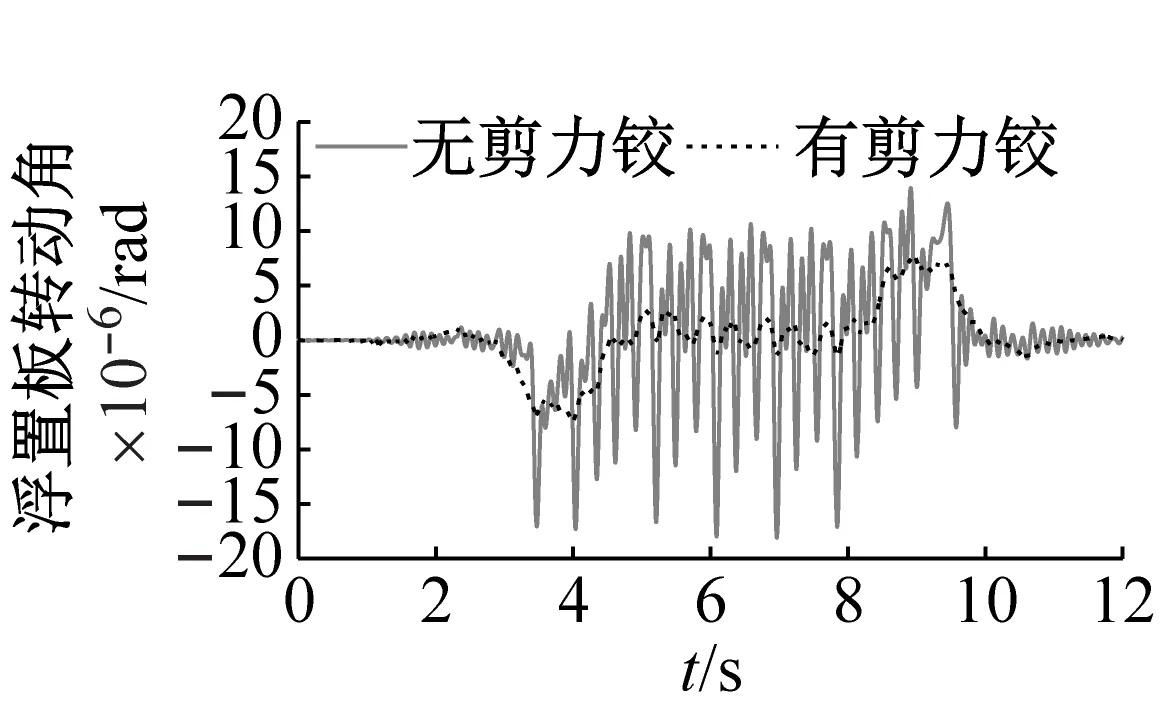
(b) 浮置板水平面内转动角

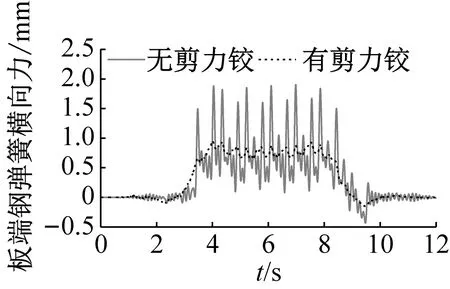
(c) 板端钢弹簧横向力

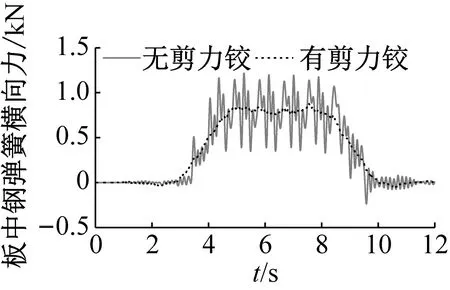
(d) 板中处钢弹簧横向力

(e) 板端扣件横向力

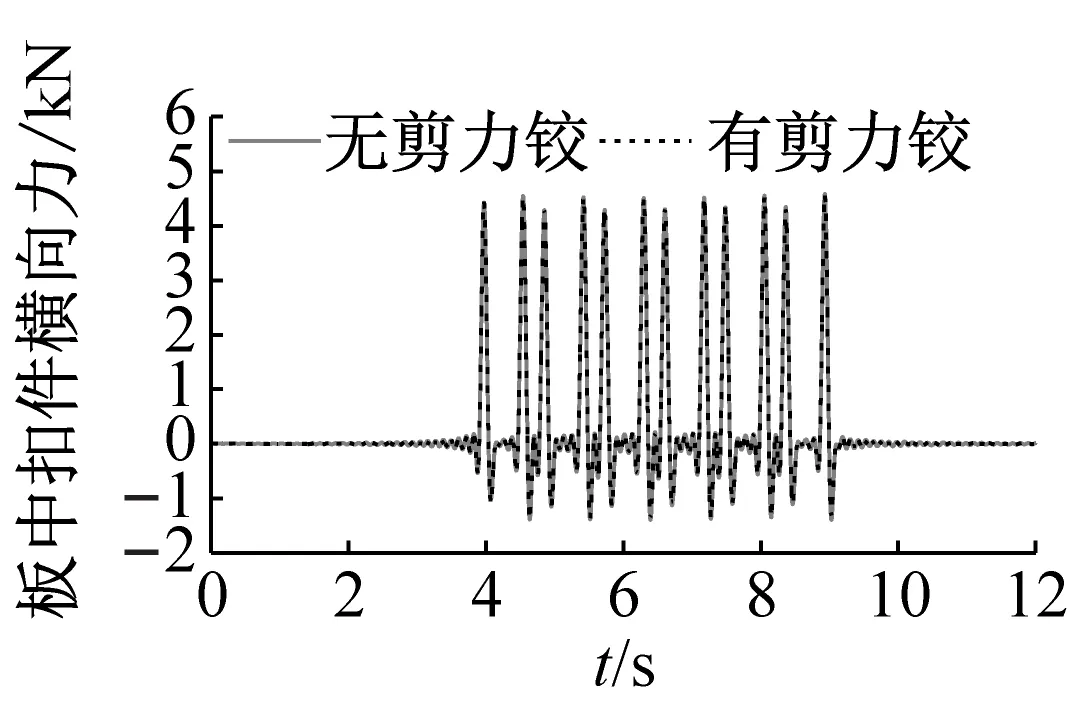
(f) 板中扣件横向力

图9 曲线段浮置板剪力铰对轨道横向动力学响应的影响

Fig.9 Influence of hear hinges on dynamic behaviors of the track with curve track

4 结 论

本文考虑了剪力铰对浮置板的横向、垂向约束作用，采用横向和竖向剪切弹簧模拟剪力铰的力学行为，基于车辆-轨道耦合动力学理论，建立了剪力铰连接条件下列车-钢弹簧浮置板轨道空间耦合动力学模型。通过仿真计算与实测结果对比验证了模型的正确性。利用所建立的模型分析了无轨道不平顺激励下，列车运行于直线线路和曲线线路时，剪力铰对列车-轨道耦合系统动力学行为的影响，研究结果如下：

(1)浮置板剪力铰能明显改善轮轨相互作用关系，减弱列车轮对通过浮置板接缝时轮轨横向力和轮轨垂向力的冲击现象，总体上使得轮轨力的变化更加平缓，也使得轮载下钢轨位移明显减小。在直线线路上，列车通过浮置板接缝位置时的轮轨垂向力变化幅值减小1/3。在曲线线路上，通过接缝位置时的轮轨横向力变化幅值减小65.9%。

(2)浮置板剪力铰能改善列车的振动，浮置板剪力铰对轮对振动的影响最大，对构架振动的影响次之，对车体振动的影响最小。在直线线路上，列车通过浮置板接缝位置时轮对质心垂向加速度减小了18%，使轮对和构架通过浮置板接缝时的垂向加速度波动由两个连续“M”形变为了一个“M”形。在曲线线路上，剪力铰能明显减弱轮对和构架的横向振动加速度。

(3)在直线线路上，剪力铰对板端扣件受力情况的改善最为明显。安装剪力铰装置后，板端扣件受力的状态明显改善，最大压缩力减少了40.7%，最大拉伸力减少了88.1%，最大峰峰值减少了56.8%。在曲线线路上，剪力铰对浮置板的横向位移、水平面内转动角、钢弹簧横向力的改善比较明显，对扣件横向力影响较小。