智能变电站控制系统多尺度失效性预测研究
李 莉, 师 鹏, 赵建利, 杨 丽
(1. 石家庄学院 机电学院, 河北 石家庄 050000;2. 河北轨道交通职业技术学院 宣传部, 河北 石家庄 050000;3. 国网河北省电力公司电力科学研究院, 河北 石家庄 050000)
在现代信息科技发展的推动下,智能变电站技术得到了广泛的应用,极大地促进了国家电网的发展[1-3],也是我国电力行业发展的重点技术。智能变电站的信息一体化平台实现了电力流、信息流、业务流的有机融合,实现了变电站的全景数据采集和数据共享。智能变电站基于IEC61850标准的统一建模和信息通信,将全站数据信息进行融合,支持高级应用,并与调度中心互动,实现全站信息的标准传输[4-6]。
智能变电站设备多、管理单元多、不确定性因素多、通信网络复杂,可以将其视为一种维数多、多个输入输出的结构复杂系统[7-8]。多尺度几何分析(multiscale geometric analysis, MGA)是基于小波分析发展起来的、可以有效处理高维函数问题,是一种致力于寻找有效的高维信息表示的新的调和分析工具,可以用于检测、表示、处理智能变电站高维空间数据。目前,人们提出的多尺度几何分析方法主要有:Ridgelet transform、Monoscale ridgelet transform、Curvelet transform、Bandelet transform、Contourlets transform、Brushlet、Beamlet、Wedgelet、Directionlet 、Wavelet transform等[9-10]。智能变电站需要利用多尺度几何分析法来分析变电站系统的复杂性和不确定性,采用变换系数的融合处理,获取变电站度量指标,实现变电站动态自动识别,为安全运行提供更为科学的理论支撑。
1 智能变电站控制系统多尺度失效性预测模型
为了解决智能变电站控制系统多尺度失效性预测模型的动态变化问题,采用定性而不是定量的方法。在定性模型中,失效性的学习情况通过对器件失效性的分析得到,而建模则是对器件的正确或错误动作作出推理的过程。
1.1 系统失效度的计算
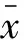
(1)
由此可见,p值越大,器件的失效难度越小;p值越小,器件的失效难度越大。当测试运行事件为二值数值(即0、1评分)时,上式可变形为
(2)
式中N是被测试器件数目,R是正确运行器件数目。形式为多个测试事件同时发生时,能正确运行的器件可能会受系统整体性能的影响。对此,可以用以下公式表达:
(3)
对失效难度指数p进行校正。其中,Cp是校正后的失效难度指数,k是每个被测器件可供选择的运行状况。
1.2 失效难度指数与方差的关系
当失效度以0、1评分时,失效难度指数p是N个受测器件中通过测试器件的平均数。
(4)
即∑x=N·p。测试成功的平方和是
∑x2=12+12+12+…+02+02=N·p
(5)
由原始数据计算方差,得
(6)
由此可知,通过测试器件比率与没通过测试器件比率之积正是测试得分的方差。
1.3 难度对信度与效度的影响
测试数据的方差可由各个测试器件得分的方差与协方差求得:
i≠j,i,j=1,2,…,n
(7)
式中pi,qi分别是器件i测试通过与测试没通过的比率,rij是测试事件i和测试事件j之间的相关系数。式(7)可变形为:
(8)
式(8)左边代表测试事件的信度指标。当等式右边的ri j增大时,等式右边随之增大,信度也增大。
1.4 多尺度区域划分
1.4.1 定义
定义一:组成失效组织管理层的元素被定义为学习对象vij,vij=〈flag,X〉。vij(i,j∈N,i≤6)代表第i层第j个对象,flag记录这个节点是否被完成,-1表示节点正在被进行,否则,flag代表学习者在该知识节点上的登记或水平。X代表一个由名称和值组成的数组,该数组提供一个学习知识对象的外部属性。X={name:value},name是一个属性名称,value是结果。这个数组给这个对象定义适应性。如果vij处于第六层则有4个额外的属性。
定义二:失效库为失效和测试的一个储存库。
定义三:知识细胞v6j(j∈N)是一个最小和最基本的知识单元,它包括下面的属性v6j=〈c,y,t,s〉。c表示认知类型:识记、理解、应用、分析、综合、评价。y里程碑标志:-1指知识细胞的里程碑,否则指向里程碑的指针。t表示测试资源的ULR,测试资源包括3个部分:与v6j相关的资源,与里程碑相关的资源和这些资源相关的估价。s设置多媒体格式可用性s={ui,s|s∈MDF,ui,s是s的URL,i∈N}。
定义四:里程碑表示知识细胞层的一个关键的节点,这个定义提供一个学习过程的跳跃机会,这个里程碑可以被器件和测试项选择。
定义五:测试关系是指器件测试之间的关系,包括顺序关系、部分关系和同步关系(没有先后关系),分别用m、s、l表示,如表1所示:

表1 现存知识关系
定义六:MSFP的格式为MSFP={V,{E}},LOE为学习对象实体。
(9)
对定义六作如下说明:
(1) 由一个独立的节点v11处于第1层仅代表学习资源;
(2) 对于任何节点〈vij,vij〉∉E,本身没有节点关系;
(3) 〈vik,vi-1,k〉∈E显示了一个部分关系,也就是Vi-1,k是Vi,k的一部分,如果一个学习者学习了Vi,k则它一定学习了该节点之前的所有的节点;
(4) 〈vij,vik〉∈Ebut〈vik,vij〉∉E表示先后顺序关系;
(5) 〈vij,vik〉∈Ebut〈vik,vij〉∈E表示同步关系;
(6) 〈vij,vi-1,k〉∈Eand〈vij,vi-1,1〉∈E(k≠1,i≠1,4,5,6)有一个相互制约关系。
1.4.2 在多尺度区域划分
步骤1:采用多尺度几何分析方法进行变换系数,经过融合处理后进行状态区间的划分,确定区域能量比为re,
(10)
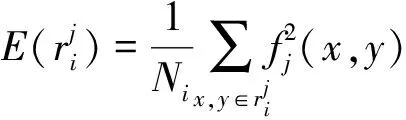
j=a,b;n和m分别为状态空间矩阵的行和列。
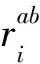
(11)
步骤2:根据尺度选择半径为r,系统共有11个设备单元:交换机、路由器、保护单元、测控单元、变压器单元、低压侧合并单元、低压侧智能终端、中压侧合并单元、中压侧智能终端、高压侧合并单元、高压侧智能终端。有6个管理工作站,分别是远动站y6、工作站y5、变压器站y4、低压侧站y1、中压侧站y2、高压侧站y3。对于系统评价指标进行弱化与强化,根据对比公式rc。
(12)
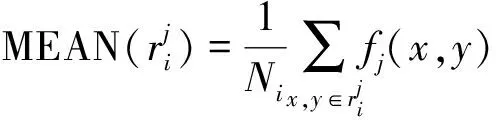
(13)
步骤3:设失效记录集中有n条失效记录值D={γ1,γ2,…,γn},每条记录有m个描述项描述其特性P={p1,p2,…,pm},D与特征集P的模糊关系可用矩阵R=(rij)n×m表示,而rij可由模糊统计得到。
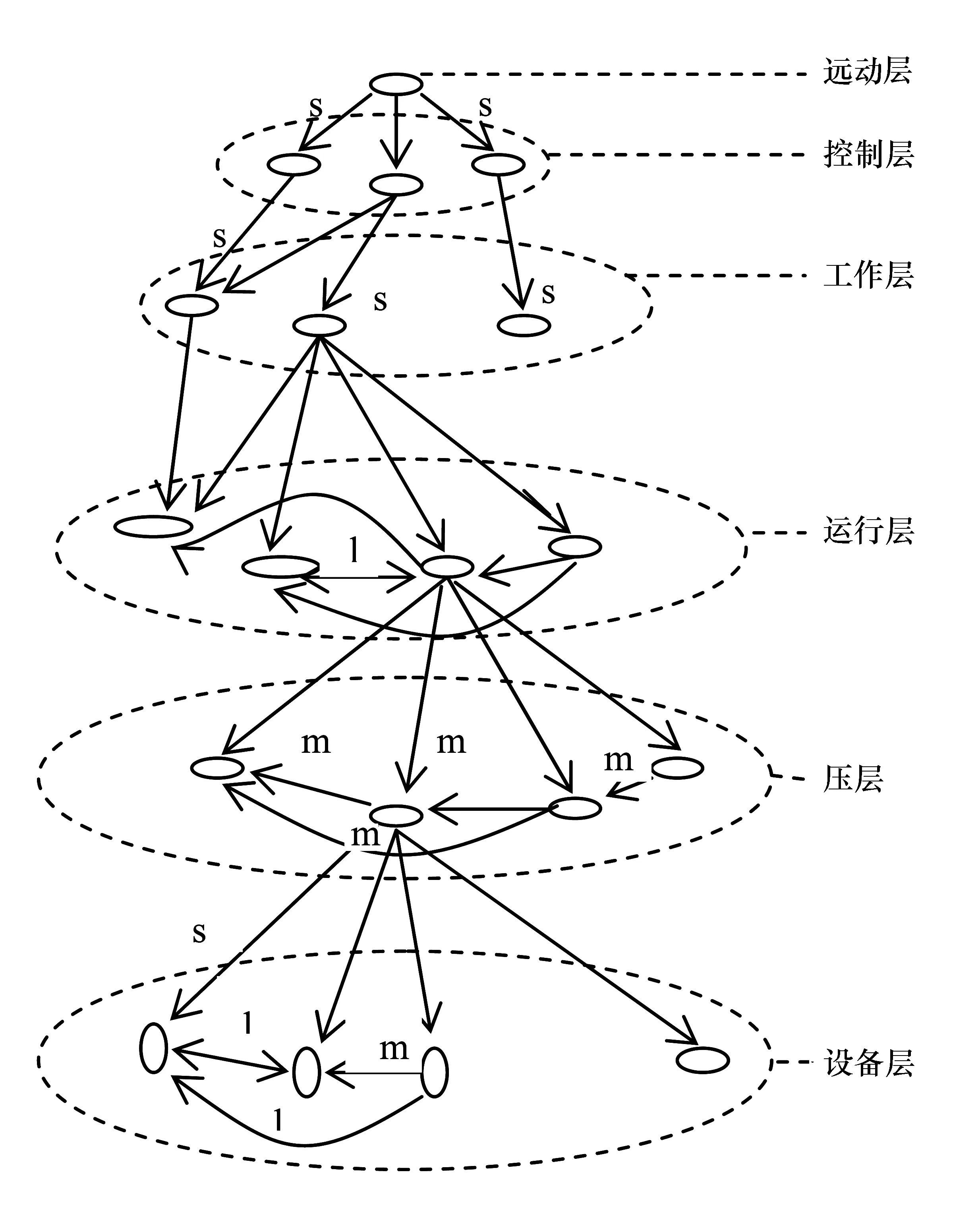
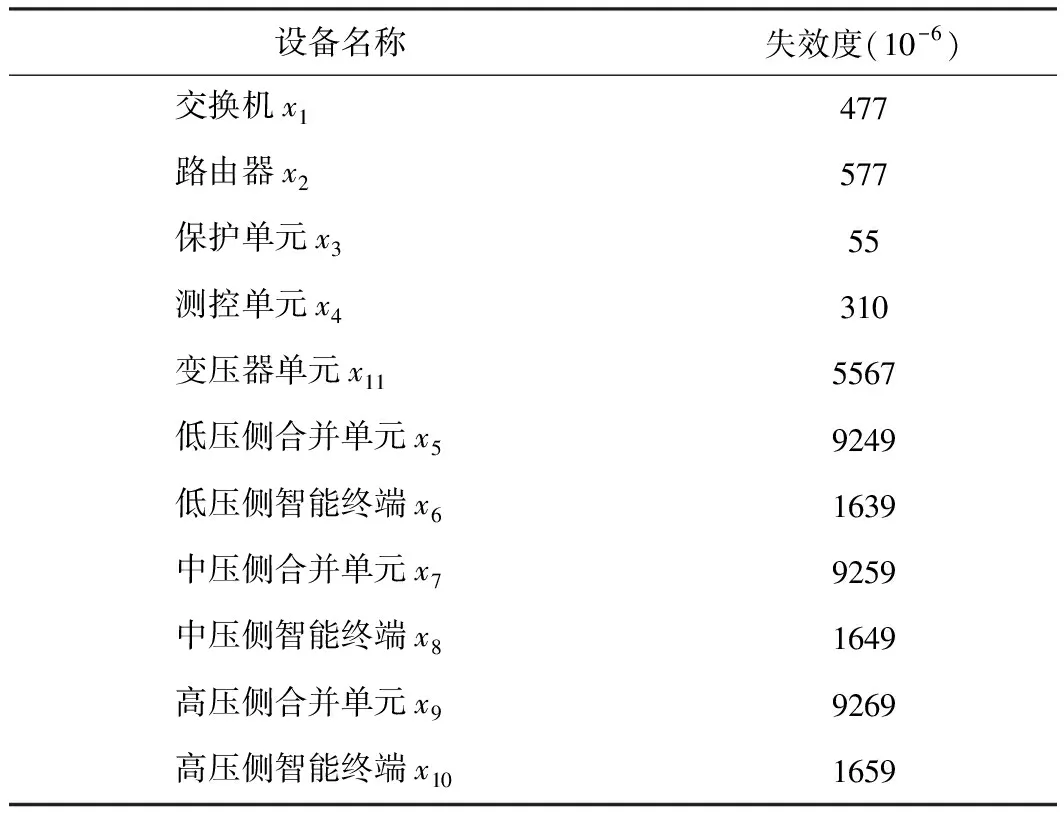
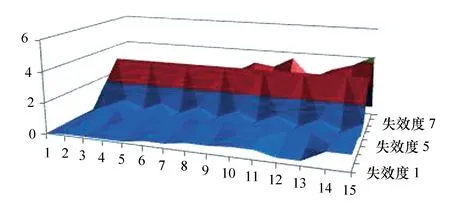
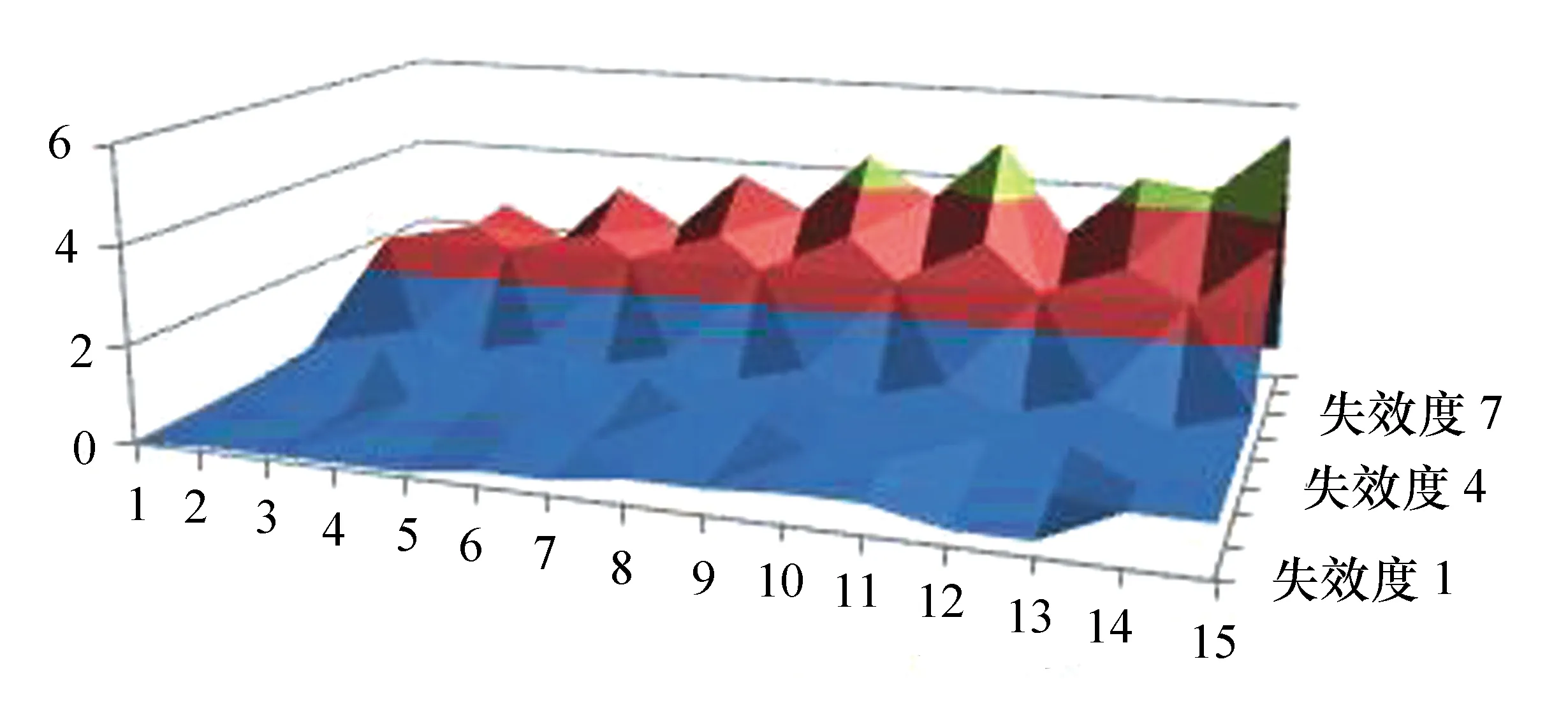
步骤4:设器件的失效记为A=Vk·ak,其中ak(第k个失效事件)是失效特征集P上的模糊集合,ak对于P的隶属失效函数ak={v1k,v2k,…,vmk},k=1,2,…,l,此vjk表示ak对特征失效属性pj的占有程度。确定优选系统失效阀值增量Q,0.5 步骤5:设矩阵S=(vjk)为m×1阶矩阵,称 (14) 为失效记录值γi记录对被测器件失效度的相近度,亦是γi与ak按定义所给的失效贴近度,表示记录值γi对系统ak的符合程度。令M=maxβik,m=minβik;其中 1≤i≤n,1≤k≤l,记δ=m+0.618(M-m)为优选值,η=m+0.618(M-m)Q为扩选值,变换βik,得: (15) 以某220 kV智能变电站为例。该智能变电站的远动站、工作站、交换机、路由器、保护单元、测控单元、变压器单元、合并单元、智能终端构成系统的失效因素合集。各部件故障程度不同,系统整体发生故障也具有不确定性。根据多尺度分支理论,将远动站作为顶层事件,则智能变电站失效性故障图如图1所示。 图1 智能变电站失效性故障图 先分别进行多尺度几何分析方法正变换,得到多尺度融合变换关系图,针对这些变换的系数,采用不同的融合策略进行融合处理,形成新的融合的多尺度方向;再对这些融合后的变换系数进行多尺度几何分析方法的逆变换。给出了变换后的多尺度融合关系图如图2所示,它有6个层次,即远动层、控制层、工作层、运行层、压层和设备层。 图2 多尺度融合变换关系图 进行控制系统自适应测试,首先确定测试参数。要准确计算控制系统器件工作值和失效信息值,需要完成区分度、难度、模糊度3个参数比较准确的计算。根据反应矩阵,对m个器件的能力值θj(1≤j≤m)、n个测试的区分度Ai、难度Bi、模糊度Ci(1≤i≤n)。 计算所得测试的均方差B: 其中 (16) 能力初值: (17) 第i项测试的通过率: (18) 第i项测试得分与测试总分间的点二列相关(当测验变量的一个为连续变量,另一个为二分变量时,可用点二列相关或二列相关来计算): (19) 式中mi为第i项测试通过数。校正后的第i测试通过率: (20) (21) 第i项测试的区分度值 (22) 第i项测试难度值 Bi=Zi/Ri (23) 第i项测试模糊度值 (24) 以L(ui|θ)表示能力为θ的被测器件对测试i的反应为ui(若测试通过,ui= 1;若测试不通过,ui= 0)的概率。 本系统采用项目反应理论的三参数模型: (25) 给定了θ,a,b,c参数后的条件概率为: (26) 可以理解为,具有水平θ的被测器件,对于第1,2,…,n项测试的通过的概率,对每一个反应向量(u1,u2,…,un)求出相应的θ值,使似然函数的值为最大。对式(26)两边取对数: (27) 令l=log[P(u|θ,a,b,c)],式两边求导: (28) 首先对数似然函数对θ的一阶偏导: (29) 其次对数似然函数对θ的二阶偏导: (30) 最后求出迭代公式: (31) 测验中各个测试事件的难度必须与测验的性质、目的相协调。尽管失效难度适中的测验以难度指数0.5为宜,但并不是一个失效测验每一测试事件的难度都为0.5。因为这会使测验分数的分布呈双峰状态,50%的器件将所有测试事件都通过,另外50%的器件将所有测试事件都不通过。失效难度应有合理的分布,如分布在0.30~0.70,这样可使测验的数值接近正态分布,并使测验的难度适中。 根据实例中控制系统的结构和多尺度融合变换的相关理论,以及表2中的数据,可以得到x1—x11失效程度为1时的可靠性数据。 表2 变电站控制系统各部件数据 不断抽取与受测器件运行能力相适应的测试,是失效测试的基本原则。通常利用测试库中测试目的最大信息函数来确定所选择的测试。用测试目的信息函数I(θ)来表示测试参数与受测器件能力的关系: (32) 式中θ为受测器件运行能力估计值,ai,bi,ci分别是第i项测试的区分度、难度和模糊系数,信息量具有可加性,可以随时估计一组测试施测的信息量的总和。对于不同能力的受测器件,测试项有不同的信息量,当信息量取最大值时,它所对应的运行能力值即是最适合于采用此项测试的器件的能力值。在系统测试中,根据前面推测的能力值,系统搜寻相应信息量最大的器件进行测试。以能力估计值达到预定的精度要求作为终止条件,即当受测器件的能力估计值逐渐稳定下来时,便可以结束测试。 用Matlab语言编程对表中的数据处理,得到工作站y5、远动站y6的失效度如图3、图4所示。 图3 工作站y5失效度图 图4 工作站y6失效度图 作为输入的低压侧合并单元x5、低压侧智能终端x6、保护单元x3和测控单元x4等,对系统的输出失效度是受输入失效度的影响的,且随着输入失效度的增加而增大。计算结果表明,当被测器件出现较为严重的故障时,被控系统有很大可能性出现严重故障,与实际相符。利用多尺度预测分析智能变电站系统失效的模糊可能性,为智能变电站整体运行、状态监测和定期检修提供了有力的理论证据。 针对智能变电站结构复杂,传统控制方法难以取得较好控制效果,本文提出了智能变电站控制系统多尺度失效性预测方法,采用多尺度几何分析方法对智能变电站失效性故障进行处理,经过变换系数、融合处理后进行状态区间的划分。采用高维系统信息表示和分析,省去了参数辨识这一步,在智能变电站预测控制中,大大减少了系统的计算负担,实现对系统的失效性的预测控制。仿真算例证实了该算法的有效性。2 智能变电站实验仿真测试


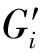


3 结语

