公路边坡预应力锚索锚固段长度探讨

蔡建伟 王艳丽

（1.云南武倘寻高速公路有限责任公司，云南 昆明 651500）

（2.云南交投公路建设第二工程有限公司，云南 昆明 650000）

根据锚固方式的不同，岩土锚固可以分为三个大类：第一类是机械式锚固，如涨壳式、倒楔式；第二类是摩擦型锚固，如缝管式锚、胀管式；第三类是注浆式锚固，该类又分为水泥注浆和树脂注浆两种。前两类锚固主要用于临时性支护工程，后一类锚固在永久性锚固工程中较为常见。注浆式锚索（杆）加固设计的一个参数就是内锚固段长度的合理确定，它的确定应该做到既安全又经济。因此，内锚固段长度临界值是锚固支护设计的关键参数，会影响整个的锚固系统的有效性。

1 理想弹塑性荷载传递模型

根据学者的研究成果[1]，基于荷载传递法研究锚索（杆）P－S 曲线特性是常用的思路。可基于P－S 曲线特性确定极限承载力与长度的关系，研究临界锚固长度的确定方法。内锚固段荷载传递模型采用理想弹塑性模型[2]，如图1所示。

图1 理想弹塑性荷载传递模型

λ为侧摩阻刚度系数，表示摩阻力发挥的强弱。侧摩阻刚度系数与锚筋表面的粗糙程度、灌浆压力、灌浆次数等有关[3]。实际工程应用中，由于无法直接测量侧摩阻刚度系数，一般是依靠拉拔试验获取锚固的P－S关系来计算得到λ参数值。

图2 处于弹性阶段的锚固地体

2 临界锚固长度计算

临界锚固长度是与极限承载力无关的锚筋长度。下图（图2）是岩土锚固分析的示意图。

图2 处于弹性阶段的锚固地体

式中，la为锚固段，lf为自由段，P 为拉拔荷载。B 为锚固体前端截面，C 为锚固体末端截面。

锚固体采用理想弹塑性模型，当锚固体前端B 截面处达到极限摩阻力时，锚索（杆）达到极限承载力；在达到极限承载力之前，锚固体处于弹性工作状态[4]。此时，在轴向抗拔力P 作用下锚固体的锚筋注浆体粘结界面的位移u(x)应满足如下方程和边界条件[2]：

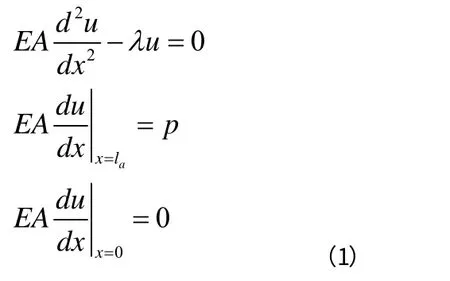
求解方程可得筋注浆体粘结界面的位移u(x)为：

摩阻力τ分布为：

B 点摩阻力τB为：

当B 点达到极限摩阻力时，锚索（杆）达到极限承载力Pu，可得：

由式5，当kla＝4 时，tanh(kla) = 0.999 ≈ 1，此时Pu达到最大值，记做Pumax；Pumax与内锚固段长度la无关，即：

根据前面的定义，临界锚固长度为：

由上式可知，临界锚固长度与侧摩阻系数的平方根成反比，与锚筋弹性模量的平方根成正比，与锚筋的横截面面积的平方根成正比。

设图2中D 点坐标为y，则CD 区域提供的抗拔力为：

根据有关研究，摩阻力主要集中与锚固段前2/3 段，因此后1/3 段锚固体提供的摩阻力大小可以用来表征摩阻力分布的不均匀性[5]。图3是图形化的计算成果，展示了不同锚固长度下后1/3 段锚固体提供摩阻力占总摩阻力的比重。其中横轴为l a/lc，表示实际锚固长度与临界锚固长度的比率；纵轴为Py/P，表示图2中CD 段分担的荷载比重，反映摩阻力分布不均的情况。

图3 不同锚固长度下摩阻力分布

3 设计临界锚固长度

通过以上分析可见，锚固长度不应小于0.5l c[6]。定义0.5lc为设计临界锚固长度，并记为。为区别起见，称lc为理论临界锚固长度。

云南某高速公路五合同段K541+540～+760 左侧第二级边坡上的锚索，有关参数如下，锚索：4Φ15.24mm，自由段长度：7m，锚固段长度：10m，为水泥砂浆预应力锚索，锚孔直径：110mm，钢绞线弹性模量E：195GPa，钢绞线横截面积A：560mm2。实测P-S 曲线如图4所示。

图4 锚索抗拔试验的P－S 曲线

根据实测P－S 曲线反演，得λ=10.16。则理论临界锚固长度为13.11m，设计临界锚固长度为6.56m。在该实际工程中，锚索的内锚固段长度超过工程临界锚固长度而小于理论临界锚固长度。

4 结语

目前，锚索结构呈现出多元化和复杂性，但是在实际应用中最多的还是拉力集中型锚索。国内目前公路边坡预应力锚索的内锚固段长度大多在8m 以上。由此看来，在实际工程中，由于盲目追求工程的安全可靠度，忽略了岩锚的荷载传递机理，设计都偏于保守。因此，为提高锚筋的利用效率，获得良好的经济效果，且保证锚固工程的安全可靠，建议内锚固段设计长度宜介于0.5lc～lc之间。