简支钢-混凝土组合箱梁的剪力滞效应分析

史子鹏

（中铁第一勘察设计院集团有限公司 710043）

0 引言

钢-混凝土组合箱梁合理地结合了两种材料的力学性能优势，上部混凝土板受拉，下部钢梁受压，已发展了多种组合截面形式且应用到各种桥梁体系。在外荷载作用下，沿混凝土上翼板和底部钢板宽度方向的应力不均匀分布称为剪滞效应。初等梁理论下的均布应力与剪滞效应应力存在明显差异，顶部与腹板连接处应力集中可达到10%～30%。为确保结构安全，必须对剪力滞效应加以研究明确，本文尝试采用三次型翘曲位移函数来给出简支组合箱梁的剪力滞效应解析解。

1 控制微分方程

本文研究模型为混凝土板与钢箱梁组合的等截面，计算模型如图1所示[1]。梁长方向为x轴方向，Z上、Z下分别为上、下翼板的中平面与换算截面轴之间的距离，ξ是混凝土悬臂板的宽度系数。模型采用以下基本假定[1]：①钢和混凝土被视为各向同性材料，组合截面符合平截面变形的假设；②组合截面的中性轴是根据基本初等梁理论计算得出的中性轴；③假设翼板纵向翘曲位移是沿横向的三次抛物线函数。

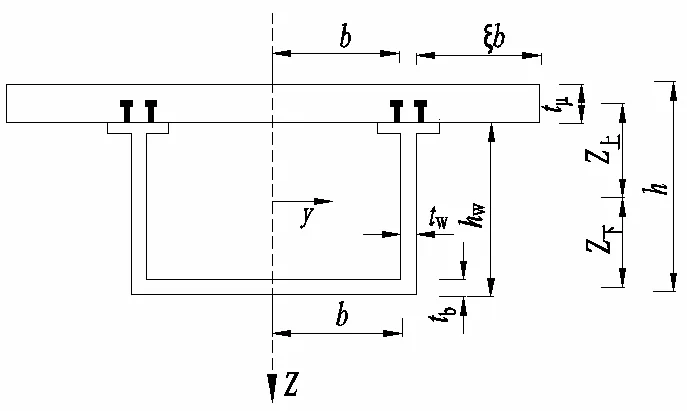
图1 钢-混凝土组合箱梁截面

引入两个广义位移概念[2]，w(x)表示梁的竖向挠度，u(x,y)描述梁的纵向位移，u1(x,y)、u2(x,y)、u3(x,y)为混凝土顶板、悬臂板、钢底板的剪力滞后位移翘曲函数，有

系统的总势能包括外荷载势能和形变势能，基于最小势能原理，在外荷载作用下处于平衡状态，对任意虚位移，系统总势能的一阶变分为0。基于最小势能原理，δΠ=0，在用分部积分法变分后，就有：

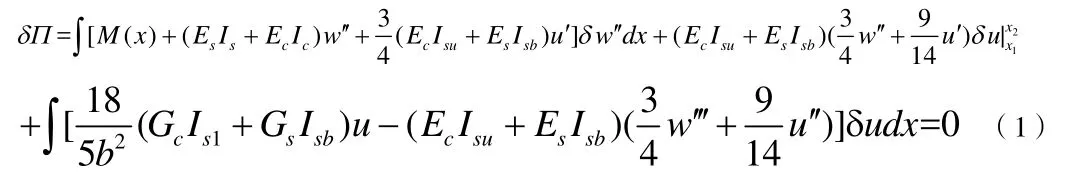
等式（1）由 δw′′和δu的任意性，得到基本微分方程和边界条件如下：

式（3）中前两式是用变分法得到的具有剪力滞效应的基本微分方程，后两式是变分所要求的边界条件。将第一个微分方程与第二个微分方程合并，消去w′，整理得：

（3）式即为剪力滞效应位移函数控制微分方程，基于能量变分原理推导得到。

2 简支边界条件下解析解

本文只选取典型的简支组合梁在承受均布荷载下的工况加以分析，简支均布荷载下，任意截面弯矩与剪力可以表示为代入（3）式后，得到剪力滞效应的控制微分方程为[3]

根据简支组合箱梁的边界条件[3]（在支点处弯矩为0），可解得

带回式（4）后得到

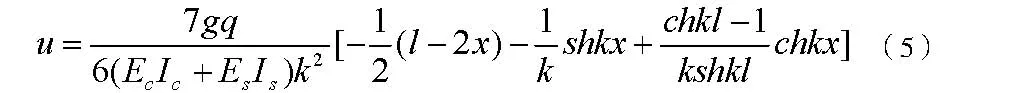
式进一步计算可得到简支均布荷载条件下，剪力滞效应影响下各部分的应力解[3]。

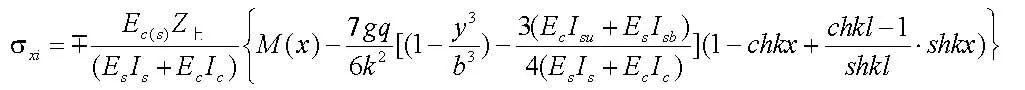
其它典型边界条件下的剪力滞解析解也基于（3）式控制微分方程，用相同的推导过程得到。

3 结论

（1）本文基于最小势能和原理能量变分法，推导了简支钢-混组合箱梁剪力滞效应的解析解，在理论上是完整的，参考均一材料的钢箱梁或混凝土箱梁理论，三次抛物线的翘曲位移函数是合理准确的。

（2）本文得出的剪力滞效应计算公式，较为明确和简单，可应用于工程实际分析。