培养学生数学运算素养案例举隅

张海强陈 刚

一、引言

解析几何强调用代数方法解决几何问题，因此，数学运算是解析几何的一项重要内容。在实际教学中，学生的数学运算能力不强是一个不争的事实。其原因可能是多方面的，比如初高中的衔接不畅，教师指导不力，学生重视不足等。由此，如何有效提高学生的运算能力，培养学生的数学运算素养是一个亟待解决的问题。

二、概念界定

数学运算是数学学科六大核心素养之一，《普通高中数学课程标准（2017年版）》（以下简称“2017年版课标”）中指出，数学运算素养是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养。主要包括：理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果；数学运算是解决数学问题的基本手段，数学运算是演绎推理，是计算机解决问题的基础；数学运算主要表现为理解运算对象，掌握运算法则，探究运算思路，求得运算结果。

江苏省2019年版考试说明中关于“运算求解能力”的考查要求是：能够根据法则、公式进行正确运算、变形和数据处理；能够根据问题的条件寻找与设计合理、简捷的运算途径；能够根据要求对数据进行估计和近似计算。

我们看到，数学运算是演绎推理，数学运算的培养必须和演绎推理相融合。关于数学运算素养的培养要结合具体内容做具体分析，不宜用大而化之的“题海战术”。以高中解析几何为例，由于高中解析几何的主体是二次曲线，因此运算对象主要是“二次三项式”，运算法则主要是多项式运算法则和分式运算法则，在运算中尤其要重视对简化和转化策略的运用。

三、案例设计

案例1 如图1设F1，F2分别为椭圆y2=1的左，右焦点，点A，B在椭圆上。若则点A的坐标是_______。

本题是想让学生明晰处理方程组是解决解析几何试题的基本技能，消元则是处理方程组的基本方法。学生在初中阶段较为系统地学习了一元一次方程、二元一次方程组、一元二次方程的解法，而对三元（多元）一次方程组和高次方程的解法涉及较少。因此，在高三复习时，教师要有意识地对方程组的处理作适当的强化，以突出消元法的地位，彰显化归思想。

（1）求该椭圆的标准方程；

本案例设计旨在强化学生“整体消元”的意识。在教学过程中，教师应引导学生根据几何条件和向量条件列出方程组，即

案例3 如图2在平面直角坐标系xOy中，曲线y=x2-6x+1与坐标轴的交点都在圆C上，则圆C的方程为_______。

学生在解决本题时常采用的有如下两种解题思路：

（图2）

思路一是选择圆的标准方程，可设圆 C的标准方程为（x-3）2+（y-b）2=r2（r＞0），利用题干求得点A，B，D的坐标，进而得到答案。

思路二是选择圆的一般方程，设圆C的一般方程为x2+y2+Dx+Ey+F=0，同样由点A，B，D的坐标求得答案。

但以上两种思路都还没有达到最简，思路三是利用整体处理的方式，设圆C的一般方程为 x2+y2+Dx+Ey+F=0，令y=0，方程 x2-6x+1=0与方程x2+Dx+F=0均表示点A，B的横坐标，故这两个方程同解，所以D=-6，F=1。同理E=-2，所以圆C的方程为x2+y2-6x-2y+1=0。

教师在教学时要详细呈现上述三种思路，引导学生在运算思路和运算方法的选取方面进行对比分析。教师要向学生讲明：（1）运算方法的选择首先体现在圆的方程的选择上，思路一是选择圆的标准方程，并利用几何条件优先得出圆心的横坐标，有效简化了计算；（2）运算方法的选择还体现在局部和整体的选择上，思路一和思路二均从局部入手，计算出曲线y=x2-6x+1与坐标轴的交点的坐标，而思路三则引导学生从曲线与方程的关系入手，从整体着眼，有效避开了无效计算，减少了步骤，极大地简化了数学运算。有了不同解题思路的对比和详细讲解，才有利于学生数学运算素养的提升。

案例4 如图3，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2+y2-12x-14y+60=0及其上一点A（2，4）。设点 T（t，0）满足：存在圆M上的两点 P 和 Q，使得求实数 t的取值范围。

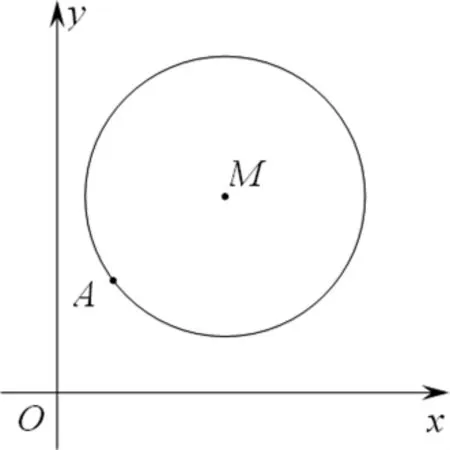
（图3）

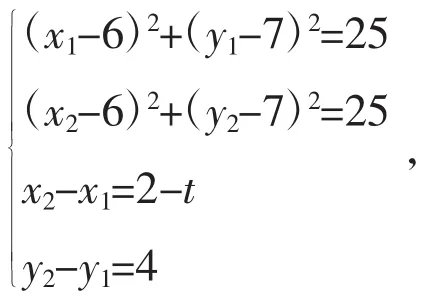
综上，我们对学生数学核心素养的培养应该精于一点，对教学资源进行充分分析。具体到学生的数学运算素养，一方面应该对部分重点内容做教学上的强化处理，另一方面则要精选例题，教会学生简化与转化的运算技巧。