基于BP-频谱扩展的多基星载SAR高分辨二维成像

肖志斌, 王鹏飞, 王树文, 郑 鑫, 张志俊

(1.海装驻上海地区第六军事代表室,上海201109;2.上海无线电设备研究所,上海201109;3.上海航天技术研究院,上海201109)

0 引言

多基星载合成孔径雷达(Synthetic Aperture Radar,SAR)由两颗及以上的小卫星SAR协同工作,以一定的基线排列在特定的轨道上,完成单星SAR所难以胜任的工作[1-5]。近年来分布式SAR发展迅速,其空间结构越发复杂,所以多基星载SAR的概念逐渐提出[6-8]。该种星载SAR系统往往具有方位、距离、高程三个维度的基线,可以同时实现合成孔径雷达二维成像、地面运动目标检测、干涉测高三大功能。

本文主要研究多基星载SAR联合二维成像算法。与传统单站SAR二维成像不同,多基星载SAR具有复杂的三维基线结构,所以在联合二维成像方面面临很多亟待解决的技术难题。首先是成像算法方面,目前主流的单站SAR成像算法,如距离多普勒(Range Doppler,RD)、频率变标(Chirp Scaling,CS)算法[9-11],习惯选择雷达波束的视线方向作为其距离向坐标轴,雷达平台运动的方向作为其方位向坐标轴,得到成像空间(即斜距坐标系)之后再进行二维傅里叶变换成像处理,但是这些算法只适用于单个雷达自发自收的成像体制,不能充分发挥多基SAR的联合成像优势。其次是成像分辨率方面,众所周知,SAR二维分辨率的提高主要依靠提高雷达发射带宽和增加合成孔径成像时间。其中,提高雷达带宽会给雷达系统的设计带来压力,并且较大的带宽会增加成像的模糊度,而增加合成孔径时间会牺牲雷达的测绘范围(如聚束成像模式和滑动聚束成像模式)。所以研究高分辨联合二维成像算法对多基星载SAR技术的发展具有重要意义。

后向投影 (Back Projection,BP)成像算法作为一种时域成像算法,相比传统的基于傅里叶变换的成像算法能够实现更高的分辨率,而且BP算法可以自主选择成像空间,这就为多基星载SAR成像带来了一定优势。比如,现有的多平台成像往往是单站SAR成像后再进行多平台图像融合处理,这个时候由于卫星对于相同目标的视角可能不同,所以需要对多幅图像进行配准[12]。而BP算法自主选择成像空间的特性使得其在一定程度下具备图像配准的能力,能够极大地简化成像的步骤。基于此,本文研究基于BP-频谱扩展的多基星载SAR高分辨二维成像算法。首先,将多基星载SAR系统中各个雷达的成像空间设为一致,并根据设定的成像空间,利用BP算法将每个雷达的回波反演到同一平面内,获得多幅单站SAR图像;然后对多幅单站复图像进行联合频谱扩展处理[13],得到相比于单站SAR具有更高分辨率的二维图像。

1 多基星载SAR回波模型

为获得多基星载SAR的高分辨联合二维图像,首先分析多基星载SAR与地面目标之间的几何位置关系,并建立其回波信号观测模型。具有N个雷达的一发多收模式多基星载SAR,可看作是共用一个发射平台的N-1组双基SAR的组合,多基星载SAR系统的观测几何如图1所示。图中P为点目标,其在坐标系中的位置为(x0,y0,z0);Rc为多基星载SAR到场景中心的最短距离;θ为雷达下视角;θBW为波束宽度。

小卫星群沿航向速度为va,假设第m(m=1,2,…,M;M为卫星的个数)颗接收卫星相对主星的基线坐标为(Brm,Bam,Bvm)。其中Brm、Bam、Bvm分别表示第m颗卫星沿航向、切航向、垂直向的基线分量。主星发射线性调频脉冲信号,信号形式为

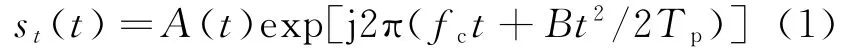
其中

式中：fc为载频;B为发射脉冲的带宽;Tp为脉冲宽度;A(t)是发射脉冲幅度的矩形包络函数;n为方位向脉冲个数;T为脉冲重复周期。

第m颗卫星接收到的位于(x0,y0,z0)的目标P的回波信号经历了双程的延时,回波的传播距离表达式为

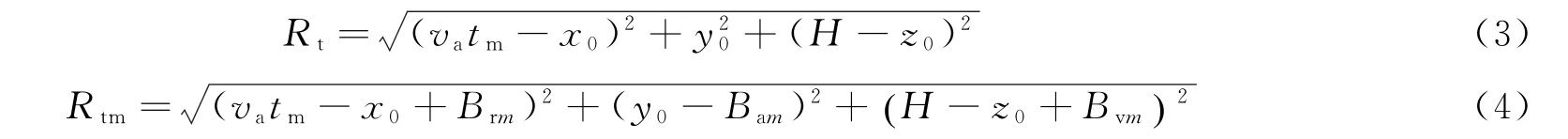
式中：Rt为发射距离;Rtm为接收距离;tm为慢时间;H为发射雷达的高度。则多基星载SAR接收到的地面目标回波信号经混频处理后可以表示为

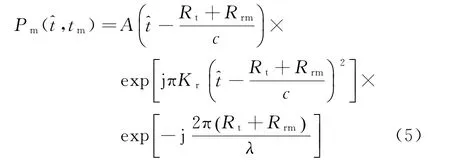
式中：为距离像快时间;Kr为发射的调频率;c表示光速;λ为发射信号波长。

2 BP-频谱扩展高分辨成像算法

2.1 BP二维成像算法

BP算法是一种时域成像算法,成像的基本原理是通过计算各个方位时刻的雷达位置与地面目标点的双程时延,找出雷达不同方位时刻所对应的回波信号,然后进行相干累加,最后得出该目标点的目标函数的过程[14-15]。该算法的优点在于,其在成像的过程中避免了不必要的近似,进而能够适应任意基线构型的多基星载SAR二维成像。并且由于其成像平面网格是自主划分的,所以在多基成像时能够将各个雷达的图像矫正到同一坐标网格中,具有图像配准能力,可以简化不同SAR图像的联合处理步骤,避免图像配准引入的相位误差。

设场景中有N个目标,经地面目标散射后雷达接收的回波信号为

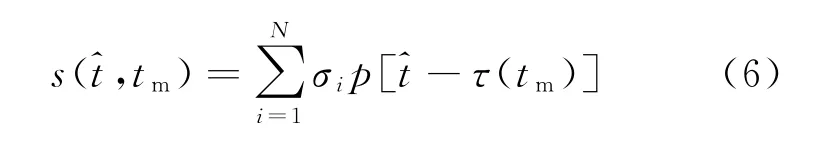
式中：σi为第i个目标的后向散射系数;τ(tm)=(Rt+Rrm)/c为回波的双程延时;p(·)表示发射的线性调频信号。第i个目标的回波信号可写为

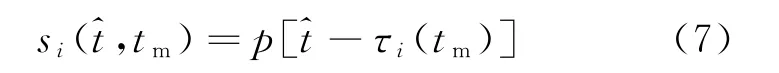
将第i个目标的回波信号与的它的复共轭进行二维相关,得到第i个目标点的散射系数,表示为

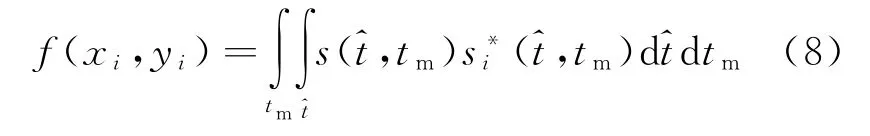
结合式(6)和式(7),式(8)可写为

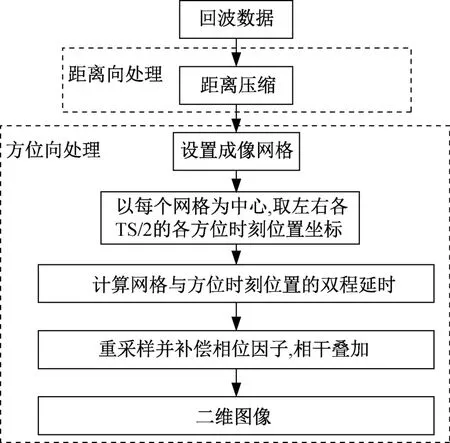
图2 BP算法流程

对卫星平台中的观测场景的某一个特定目标点(xm,ym,zm),先得出所对应的其中一个孔径中的各个方位时刻的位置与该特定像素点的双程时延τ(tm)=(Rt+Rrm)/c,再从距离压缩之后所得到的回波数据域中寻找出相对应的累积曲线,沿此曲线将所有得到的信号进行一次相干叠加,最后得出该特定像素点的能量之和,即为该点位置的成像结果。BP成像算法的成像流程如图2所示。首先对回波数据作距离向匹配滤波完成距离压缩;然后按照设定的成像网格对每一方位信号进行后向投影;最后对投影图像作重采样并补偿相位因子完成二维聚焦。

2.2 频谱扩展

多基星载SAR能够实现远超单站SAR分辨率的二维成像,归功于其空间基线的配置,即多个雷达所得到的二维复图像在距离向和方位向具有不同的频率带宽范围,通过频谱扩展技术能够获得一幅分辨率远优于单站SAR成像的图像。

多基星载SAR从不同的视角观测地面相同的成像区域,所获得的多组回波信号之间存在一定量的频偏。在估计出多基星载SAR信号间频偏的基础上,将接收辅星的频偏移动到中心发射主星的频谱之上,然后将数颗卫星的信号分别在频域进行叠加,能够实现信号二维带宽的展宽,提高成像的距离向以及方位向的分辨率。为达到这一目标,多基星载SAR系统需要满足两个条件：其一,卫星之间的方位/距离向的基线足够长,因为基线越长,相应的距离向/方位向分辨率改善越大;其二,参与频谱合成的两颗卫星所得图像具有一定相关性,故距离向/方位向基线长度不能超过极限基线。

(1)频偏估计

实现多幅SAR图像的频谱扩展,首先要估计各图像之间的频谱偏移量。以两幅图像为例,卫星A和卫星B的回波信号经BP成像处理之后的单视复图像信号表达式为

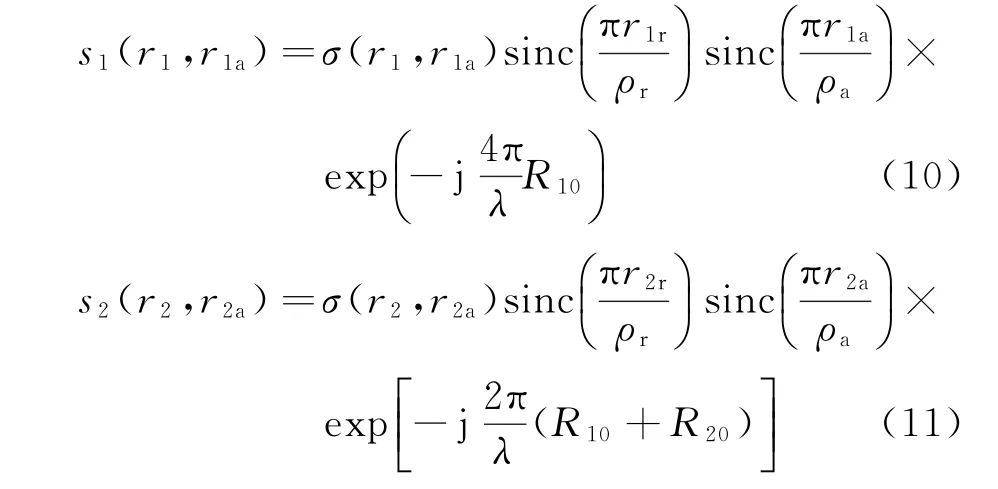
式中：σ(r1,r1a)、σ(r2,r2a)为同一个散射点在两颗卫星上的后向散射系数;ρr、ρa分别表示距离向和方位向分辨率;R10、R20分别表示卫星A和卫星B到目标的距离。从式(10)和式(11)可以看出,若采用传统的频域成像算法,由于存在空间基线的原因,卫星A、B对地面目标观测的角度有所不同,所以两幅SAR单独成像后的图像像素点不能很好地对应,而且像素单元大小也有差异,因此在图像进行频偏估计前需要对卫星A、B的图像进行图像配准。而BP成像算法,由于两颗卫星成像时划分的成像网格相同,可以实现不同平台回波信号相干累加的像素点准确对应,省去了图像配准的计算步骤。

以方位向频偏估计为例,首先对卫星A和卫星B的复图像进行相干处理,然后对获得的干涉条纹相位对慢时间求导,得出其慢时间瞬时频率为

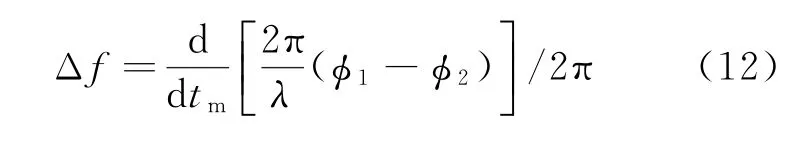
其中

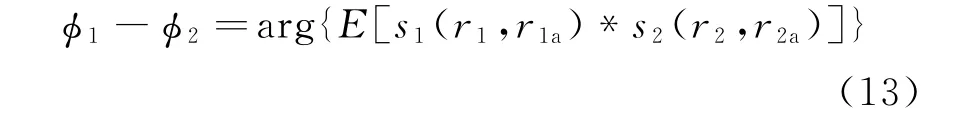
式中：ϕ1-ϕ2为互相关法估计的表示两幅复图像的相位差;arg(·)为取相位函数;E(·)表示期望。由于干涉复图像的慢时间瞬时频率就是多基SAR回波信号间的多普勒频率偏移,因此,只要估计出干涉复图像沿方位向的瞬时频率,就可以估计出方位向的多普勒频偏。其主要操作步骤如下：

a)各卫星的回波信号通过BP成像算法单独成像;

b)将接收卫星所获得的二维复图像与主卫星图像进行相干处理;

c)获取图像相干处理后的干涉条纹,利用式(13)估计两幅图像的相位差;

d)利用式(12)估计瞬时频率,获得图像的频谱偏移量。

距离向的频偏估计与方位向类似,区别在于在式(12)中将慢时间的求导改为快时间,这里不再赘述。

(2)频谱扩展

将主星与接收卫星的复二维频谱在距离向或方位向进行频谱扩展,频谱合成之后的信号为

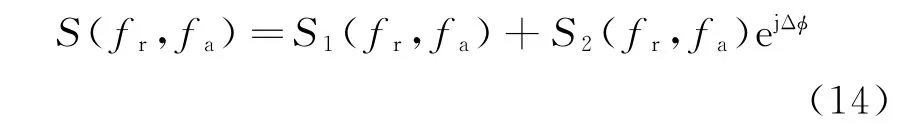
其中

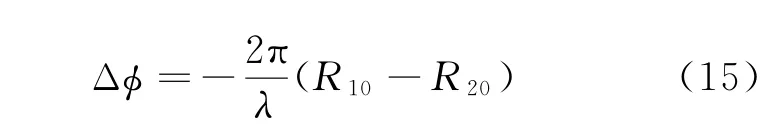
式中：Δϕ为卫星A与卫星B复图像的相位差;fr为距离向频率;fa为方位向频率。

对式(10)和式(11)进行逆傅里叶变换,并代入式(14)可得

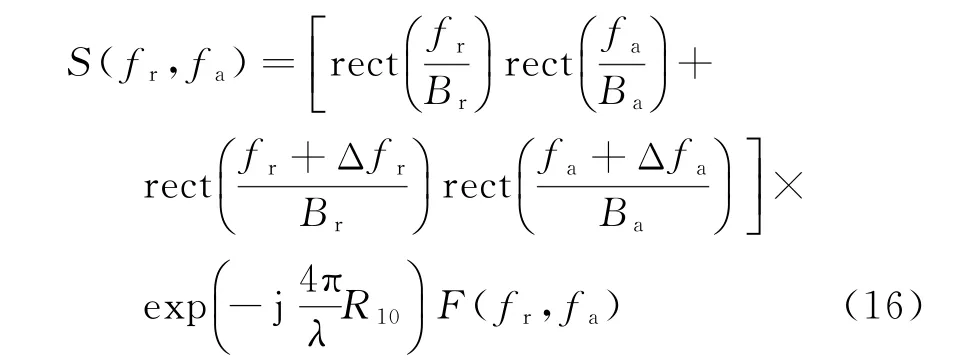
式中：rect(·)为矩形函数;Br为距离向信号带宽;Ba为方位向信号的带宽;Δfr是卫星A和B之间距离向频率偏移;Δfa表示卫星A和B之间方位向的频率偏移;F(fr,fa)为耦合频率。

当卫星A和卫星B的信号的频宽达到最大值时,频谱合成之后的频宽能够达到最大,此时经过频谱合成后的信号为

对式(17)做离散傅里叶变换,可以得到进行频谱扩展后的信号的方位向以及距离向的分辨率,其表达式为

不难发现,频谱扩展技术能够提升多基星载SAR成像的分辨率。

通过分析可以得出,多基星载SAR的斜视角、基线分布、下视角、成像模式都会对信号的频率偏移产生一定的影响。SAR信号间的频率偏移越大则通过频谱合成所增加的带宽也就越多,从而分辨率的改善也就更大[3]。但事实证明,实际背景下多基星载SAR图像间过大的频率偏移会使得信号之间的相干性降低,进而降低了干涉相位的精度,会导致频谱扩展的极大误差。所以,成功应用频谱合成方法,需要合适的基线长度来保持信号之间的相干性。

3 仿真实验

为验证本文成像方法的有效性,以某多基星载SAR系统为例,分别进行单星BP算法及双星BP-频谱扩展算法的二维成像仿真实验。

3.1 单星BP算法二维成像

单星成像仿真实验中,星载多基SAR系统主星参数如表1所示。

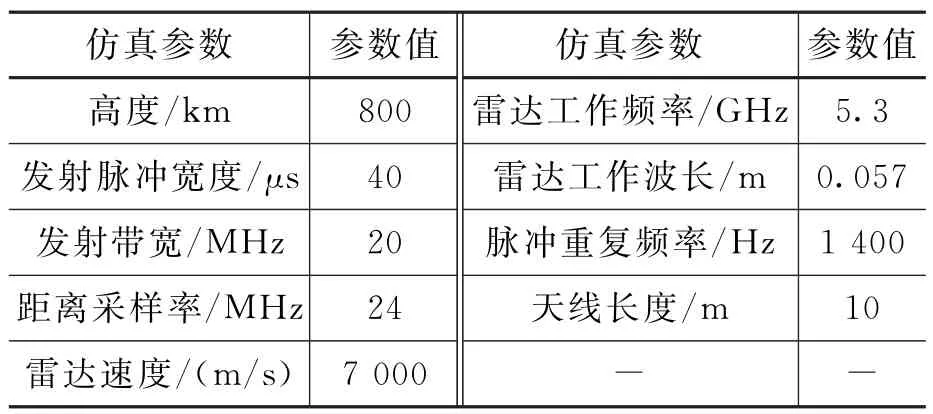
表1 星载多基SAR系统主星参数设置

根据卫星参数,选取1 024×1 024点的成像场景,设置地面点目标位于场景中心点,主星的BP成像结果如图3所示。

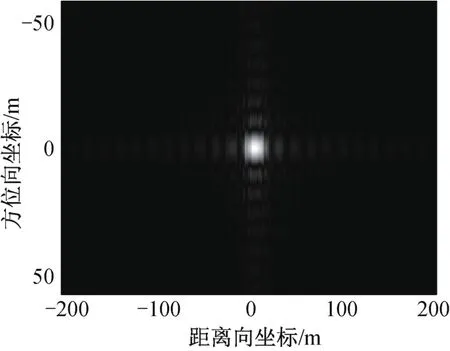
图3 主星点目标BP成像

距离向以及方位向的归一化幅度切面如图4所示。

通过距离向和方位向的归一化幅度切面图可以计算出各方向的成像质量指标,如表2所示。

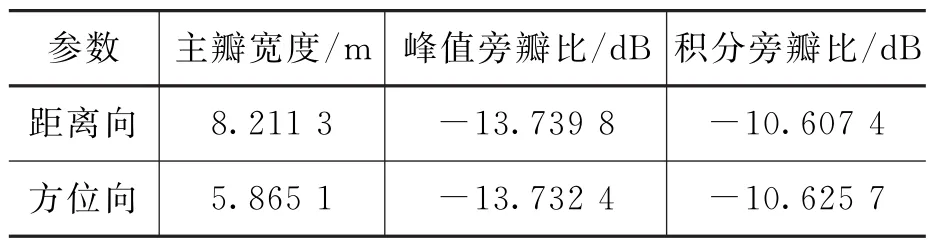
表2 主星BP成像结果指标

由表2可知,BP成像算法具有较好的峰值旁瓣比以及主瓣宽度。其分辨率也与理论值接近。

3.2 双星BP-频谱扩展算法二维成像

双星成像仿真实验分方位向和距离向两组进行,利用本文提出的BP-频谱扩展算法,分辨出单星在方位向以及距离向无法区分的目标,证明算法的有效性。

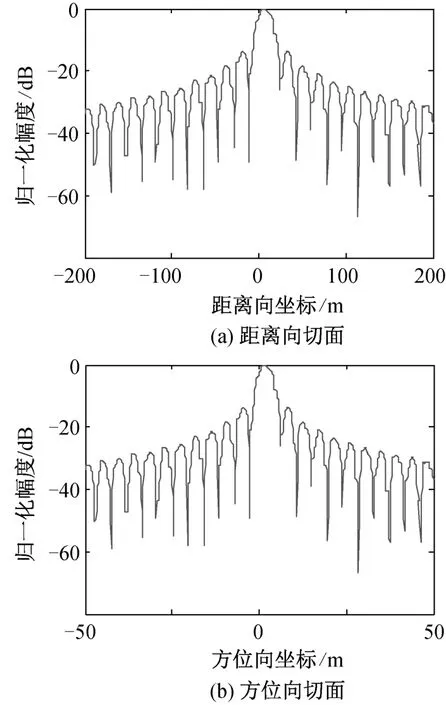
图4 主星点目标BP成像归一化幅度

图5 两颗卫星距离向分布多目标单独BP成像

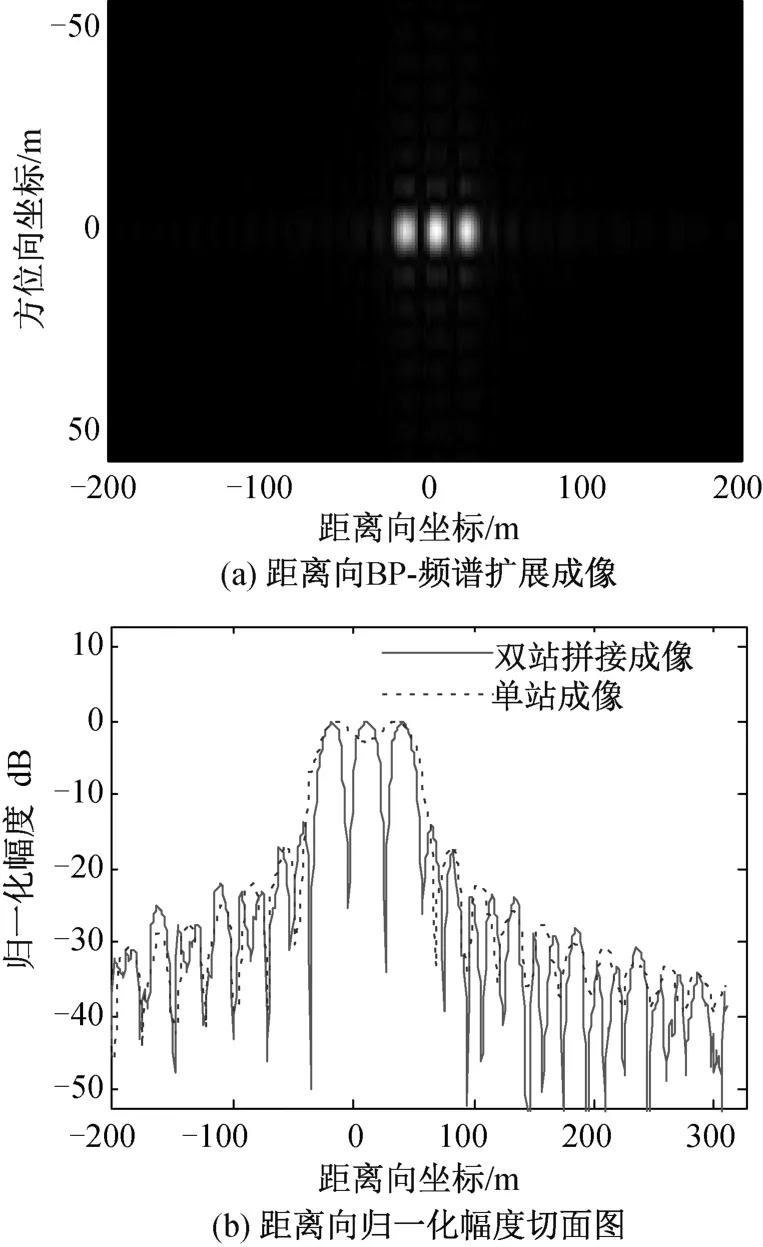
图6 两颗卫星多目标距离向BP-频谱扩展成像

首先,设置三个沿距离向分布的、位于场景中心线上的点目标,间隔取略大于主瓣宽度的10 m。多基星载SAR系统包括两个成像雷达,以主星为参考卫星,接收卫星的基线分布为(Br2,Ba2,Bv2)=(2 000 m,2 000 m,300 m),接收卫星的其他参数见表1。两颗卫星单独成像的结果如图5所示。

由图5可知,因为目标沿距离向相距太近,主星和接收卫星的单独成像均不能很好地分辨出3个目标。然而,因两颗卫星具有距离向分布的基线,所以利用本文所提算法联合成像,能够提升距离向分辨率。对两幅单视复图像进行距离向BP-频谱扩展成像,成像结果如图6所示。

由图6可知,原先单星成像不能有效区分出来的三个点目标,经过多基星载SAR BP-频谱扩展成像算法进行距离向频谱拼接之后,能够清晰地分辨出来。距离向归一化幅度切面图也说明了这点,单星已经混淆的波瓣,经过频谱扩展后分离出了三个清晰的波瓣,说明了本文算法在距离维高分辨成像上的有效性。

设置三个沿方位向分布的、位于场景中心线上的点目标,其间距取10 m,大于单星的方位分辨率。接收卫星的基线与上一个实验相同,因其具有方位向的基线,所以经过频谱扩展后能够提升方位向分辨率。两颗卫星单独成像的结果如图7所示。

图7 两颗卫星方位向分布多目标单独BP成像

由图7可知,沿方位向排列的三个点目标单星SAR成像无法完全区分出来。方位向BP-频谱扩展成像结果如图8所示。

由图8可知,原先单星成像不能区分出来的三个点目标,经过多基星载SAR方位向BP-频谱扩展成像之后,能够清晰地分辨出来。方位向切面图也说明了这点,单星已经混淆的波瓣经过合成后分离出了三个清晰的波瓣,说明了在方位维上BP-频谱扩展算法的有效性。

经过以上实验可知,本文提出的基于BP-频谱扩展的二维成像方法,能够突破传统单星SAR成像分辨率的限制,充分利用多基星载SAR空间三维基线的优势,从而提高二维成像的分辨率。

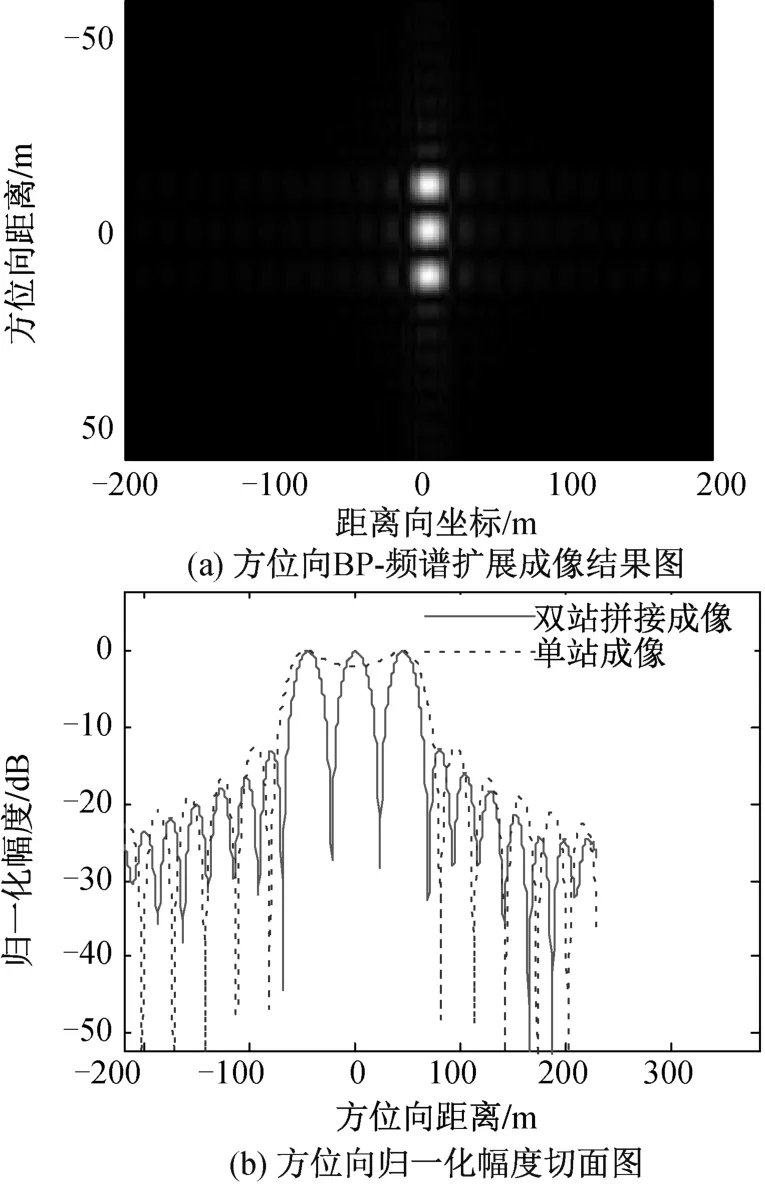
图8 两颗卫星多目标方位向BP-频谱扩展成像

4 结论

本文针对多基星载SAR这种新兴构型体制雷达,提出了基于BP-频谱扩展的高分辨联合二维成像方法。该方法在多基星载SAR背景下有以下优点：

a)对多个雷达回波信号自主划分同一成像网格,在多基星载SAR联合成像中省去了图像配准的步骤,降低了算法流程的复杂程度;

b)突破了单星SAR成像分辨率的限制条件,充分利用了多基星载SAR的三维基线信息,能够实现优于单站SAR的高分辨二维成像。