一种抑制超低频振荡的水电机组调速器参数协调优化方法研究

(1.四川大学电气信息学院，四川 成都 610065； 2.国网四川省电力公司，四川 成都 610041；3.南京南瑞继保电气有限公司，江苏 南京 211102)

0 引 言

近年来在水电机组占比较高的直流送出系统中出现了振荡频率低于0.1 Hz的超低频率振荡现象，其振荡频率显著低于低频振荡范围[1-2]。2016年3月，南方电网在进行云南异步联网试验时，出现持续时间25 min，周期为20 s的超低频率振荡[3-6]。同时研究发现当渝鄂背靠背柔性直流工程投入运行后，川渝电网也与主网实现异步联网，与云南电网情况类似，川渝电网也存在发生超低频振荡的风险。

文献[7]指出超低频振荡发生后，系统中所有发电机转速同调变化，系统频率整体振荡，可将多机系统等值为单机带负荷系统进行分析。文献[8-10]针对水电外送孤岛系统进行小干扰分析，指出水轮机调速器PI控制器的积分系数KP、比例系数KI、水锤效应时间常数Tw是影响超低频振荡的关键因素。文献[11-12]针对云南异步联网验证性试验过程中出现的超低频振荡现象，重新整定了云南水电机组的调速器参数，即将所有水电机组调速器KP减小为原来的二分之一，KI减小为原来的十分之一；但该方法没有对引发超低频振荡的振荡源进行定位，需要重新整定参数的水电机组范围过大，同时整定后调速器采用较小的PI参数将使得机组响应速度变慢，调节性能变差。文献[13-16]分析了传统直流附加频率控制器，通过其快速调节直流输送功率增强送端系统抑制频率振荡的能力；但增设直流附加频率控制器后，将导致直流输送功率随系统频率变化频繁变化，对直流系统的运行及直流受端交流系统稳定性均会造成影响。文献[17-19]采用PSS作用于发电机励磁系统，利用相位补偿原理产生纯阻尼力矩，起到抑制频率振荡的作用；但PSS主要用来抑制低频振荡，对超低频振荡没有抑制效果。文献[20]提出一种基于能量流在线评估发电机阻尼特性的方法，但能量流法没有考虑发电机动能和势能的变化，对发电机阻尼特性的评估不够准确。文献[21]为定位低频振荡源研究了发电机电磁转矩阻尼系数的辨识方法，但该方法对超低频振荡源机组的定位不够准确。

在出现超低频振荡的电网中，存在水电机组多、机组容量分散的特点。采用逐一调整水电机组调速器PI参数抑制超低频振荡的方法工作量大，并将影响电网的调频性能。因此有必要将水电机组对超低频振荡的贡献度进行评估，通过对贡献度大的水电机组调速器PI参数优化，抑制超低频振荡。

下面提出一种超低频振荡抑制方法。该方法基于子空间辨识算法和改进粒子群算法实现了对超低频振荡贡献度大的机组调速器PI参数的协调优化，相较于文献[11-12]缩小了待整定调速器PI参数的机组范围，减小了对机组调节性能的影响。仿真结果表明采用所提方法可有效抑制超低频振荡。

1 四川电网超低频振荡机理分析

渝鄂背靠背柔性直流工程投运后，西南电网与西北、华中、华东3个区域电网异步互联，四川电网稳定特性由多机系统下的暂态功角稳定问题转化为单机带负荷下的频率稳定问题。同时由于四川电网内水电机组装机容量高，水锤效应明显，使得四川电网存在发生超低频振荡的风险。

仿真结果表明，当超低频振荡发生时，四川电网内所有发电机组发生同步振荡，可将网内机组等值为单机系统。建立异步联网后的四川电网超低频振荡简化分析模型如图1所示。

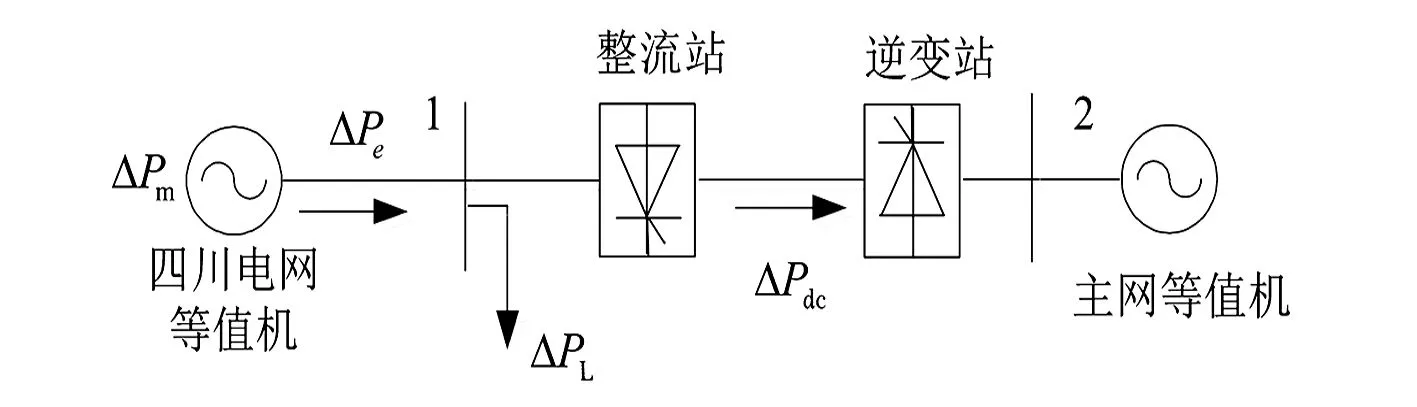
图1 单机系统模型

图1中：左侧机组为超低频振荡下四川电网发电机等值模型，经直流输电系统与主网异步互联；ΔPm为发电机机械功率变化量；ΔPe为发电机电磁功率变化量；ΔPL为本地负荷功率变化量；ΔPdc为直流输送功率变化量。列写图1中四川电网等值机转子运动方程为

(1)

式中：TJ为惯性时间常数；ΔTm表示发电机机械转矩；ΔTe为发电机电磁转矩。电磁转矩和机械转矩均可以写成阻尼转矩分量和同步转矩分量矢量和的形式。

(2)

式中：ΔTDm为机械转矩阻尼分量；ΔTSm为机械转矩同步分量；ΔTDe为电磁转矩阻尼分量；ΔTSe为电磁转矩同步分量。将式(2)代入式(1)可得

(3)

由式(3)可得发电机阻尼转矩ΔTD为

ΔTD=(-ΔTDm+ΔTDe+DΔω)

(4)

当ΔTD为负时，将导致超低频振荡发生。发电机阻尼系数D>0，始终提供正阻尼。当忽略网损时，电磁转矩可认为由本地负荷和直流共同提供，始终为系统提供正阻尼转矩。发电机机械转矩由调速器提供，当机械转矩阻尼分量为负时，将导致发电机阻尼转矩ΔTD为负，引发超低频振荡。

2 机组超低频振荡贡献度评估

当发生超低频振荡时，四川电网第i台发电机的机械转矩为

ΔTmi=KDi(-Δω)+KSiΔδ

(5)

当KDi>0时，发电机机械转矩为系统提供正阻尼，机组对超低频振荡的贡献度小；当KDi<0时，发电机机械转矩为系统提供负阻尼，机组对超低频振荡的贡献度大。

考虑多机系统下，对第i台发电机机械转矩阻尼系数在线拟合，首选对式(5)进行离散化处理得到

(6)

式中：N为采样点个数；T为采样周期；ε为线性估值的误差。发电机调速器机械转矩阻尼系数的在线辨识可以转化为线性估值问题。

ΔTmi=[ΔωΔδ]Ki+ε
=AKi+ε

(7)

定义代价函数H(x)：

H(x)=[ΔTmi-AKi]T·[ΔTmi-AKi]

(8)

当H(x)达到最小值时，Ki的估计值为

Ki=[AT·A]-1·AT·ΔTmi

(9)

当ATA可逆存在时，由式(9)即可求得发电机机械转矩阻尼系数KDi。对四川电网机组超低频振荡贡献度评估的具体步骤如下：

1)获取扰动后时段t内各机组机械功率、角速度、功角的离散时序数据；

2)计算各机组时段t每个周期T内的机械功率、角速度、功角的变化量；

3)将各机组的机械功率、角速度、功角的变化量数据带入式(9)，得到各台发电机机械转矩阻尼系数KDi；

4)根据第i台发电机机械转矩阻尼系数KDi的拟合值，评估该机组对超低频振荡的贡献度。

3 系统状态子空间辨识

考虑多输入多输出的高阶电力系统，其状态空间模型可描述为

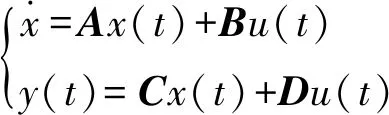
(10)

式中：u(t)、y(t)、x(t)分别为系统的输入、输出、可观测状态量；A是系统矩阵；B是输入矩阵；C是输出矩阵；D是输入直接作用于输出的矩阵。假定输入输出数据分别为uk、yk(k=1,2,3,…N)，引入分块Hankel矩阵：

(11)

(12)

式中，α为自定分块行数，为保证低秩性，α必须大于系统的阶次n。从状态方程可推导出如下矩阵方程：

Y=ΓαX+HαU+N

(13)

(14)

(15)

H、Γα分别表示广义可观测矩阵和下三角Toeplitz矩阵。当已知Γα和X时可得到系统状态空间矩阵A、B、C、D。因此在已知系统输入uk和输出yk时，辨识系统状态空间模型的方法如下：1)根据输入输出建立Hankel矩阵，并进行QR分解得到Hankel矩阵的行空间投影；2)对该投影进行奇异值分解，得到可观测矩阵Γα和状态矩阵X；3)由可观测矩阵Γα和状态矩阵X确定系统状态空间矩阵A、B、C、D。

4 超低频振荡水电机组调速器参数整定方法

超低频振荡水电机组调速器参数协调优化方法如图2所示，具体步骤如下：

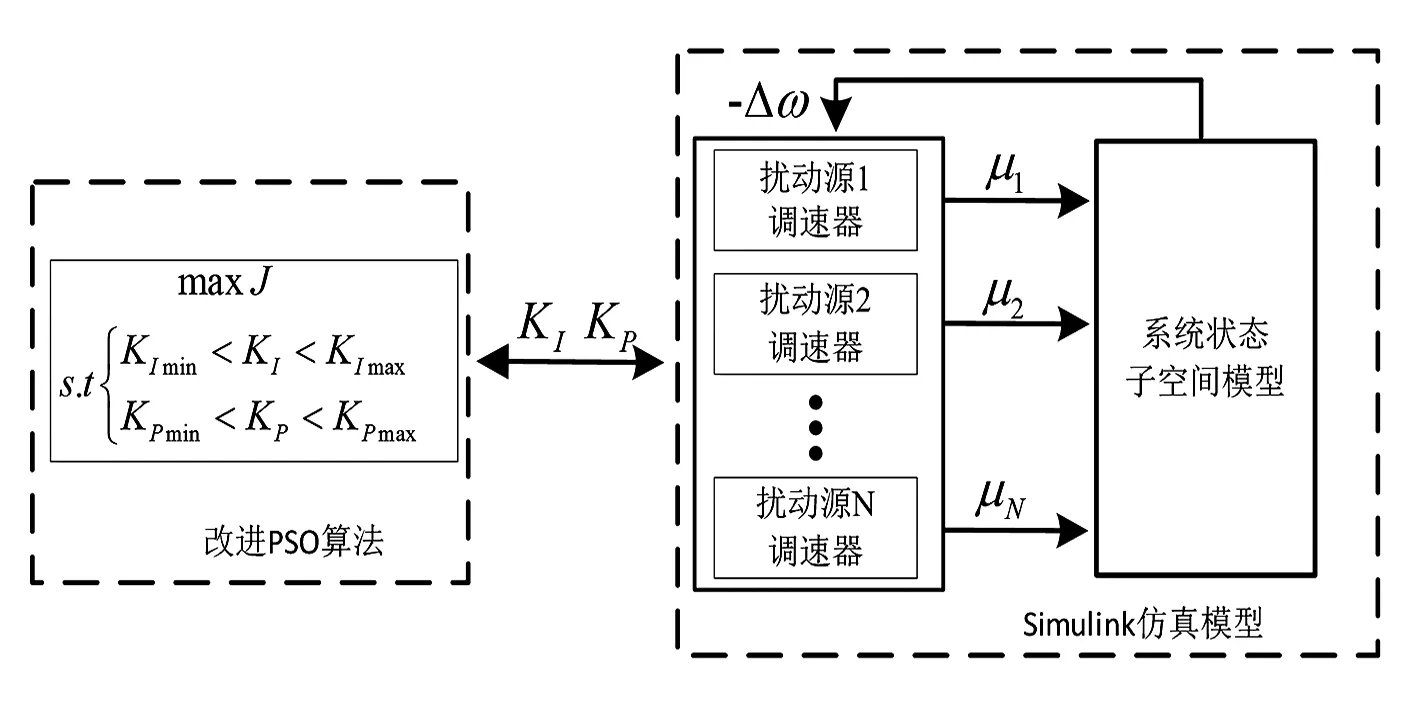
图2 水电机组调速器参数协调优化

1)在线拟合发电机机械转矩阻尼系数，筛选出阻尼系数为负，即对超低频振荡贡献度大的机组，得到待优化机组群；

2)利用状态子空间辨识算法，辨识待优化机组群的机组开Δμ到频率-Δw的系统状态子空间模型；

3)在Simulink中建立含待优化机组群调速器和系统状态子空间模型的仿真模型，结合改进粒子群算法优化机组群调速器PI参数。

5 仿真分析

针对PSASP软件EPRI 36节点标准仿真模型进行改进，删除BUS30-BUS31交流线，将BUS34-BUS33交流线替换为直流输电系统。改进后的模型含AREA1、AREA2两区域，分别代表渝鄂柔性直流投运后的四川电网和主网。

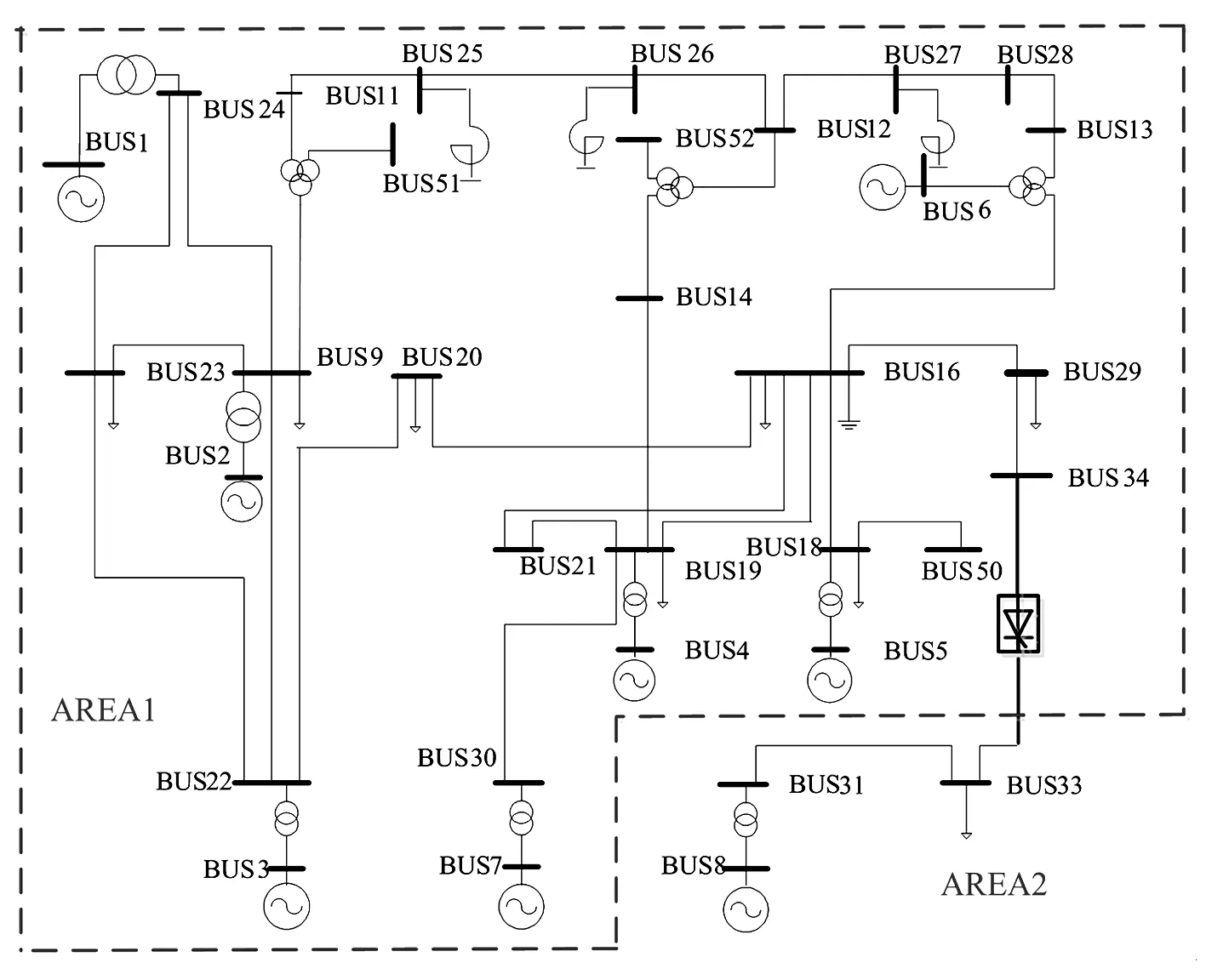
图3 EPRI 36节点系统

基于改进的EPRI 36节点仿真模型，验证所提水电机组调速器PI参数优化方法的有效性。其中AREA1含7台发电机(G1至G7)，采用PSASP软件中8型调速器模型，参数套用四川电网典型水电机组调速器参数。

5.1 负荷扰动

模拟负荷扰动，在1 s时刻，损失100 MW负荷，系统频率曲线如图4所示。

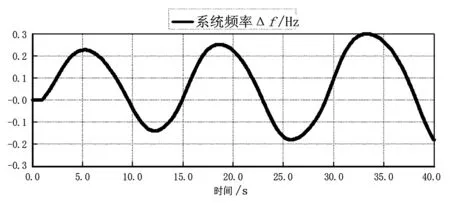
图4 负荷扰动频率曲线

负荷扰动后，频率出现超低频振荡现象，振荡频率为0.056 Hz，阻尼比为-0.12，频率振荡逐渐发散。为抑制振荡，需先对超低频振荡贡献度较大的机组进行筛选，得到待优化机组群；并以待优化机组群开度作为输入、系统频率作为输出辨识系统状态子空间模型，利用改进粒子群算法协调优化超低频振荡贡献度较大的机组调速器PI参数。

1)机组超低频振荡贡献度评估

超低频振荡发生后，拟合G1至G7发电机机械转矩阻尼系数，如表1所示。

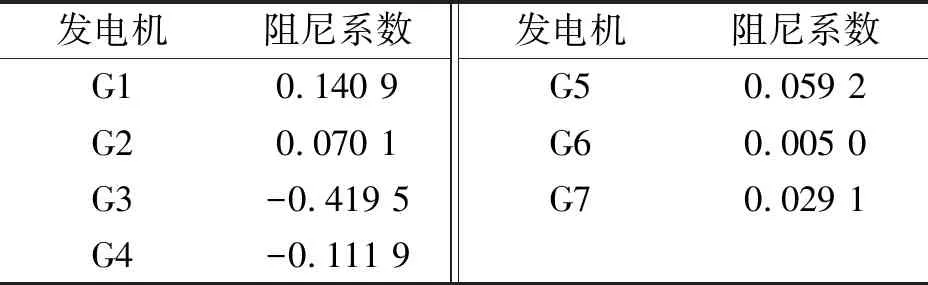
表1 G1-G7阻尼系数

由表1可知：G3、G4发电机机械转矩阻尼系数小于0，向系统提供负阻尼转矩，对超低频振荡的贡献度大；其余发电机机械转矩阻尼系数均大于0，向系统提供正阻尼转矩，对超低频振荡的贡献度小。为抑制超低频振荡，需协调优化G3、G4发电机调速器PI参数。

2)机组调速器PI参数协调优化

模拟G3、G4发电机开度阶跃扰动，辨识系统状态子空间模型。在1 s时刻，在G3、G4发电机调速器出口处施加5%阶跃扰动作为输入信号，选取系统频率变化量作为输出信号。辨识得到系统状态子空间模型矩阵A、B、C、D如下：

其中，A矩阵特征向量为-0.034 2±0.316 5i，辨识得到的系统模型自然振荡频率为0.05 Hz，与超低频振荡频率近似相同，验证了系统状态子空间模型的准确性。

结合G3、G4发电机调速器模型和系统状态子空间模型在Simulink中搭建闭环仿真系统，并利用改进粒子群算法协调优化调速器PI参数。设置惯性权重wmin、wmax、γ，粒子群规模取50，迭代次数为30次。优化前后G3、G4发电机调速器PI参数见表2。

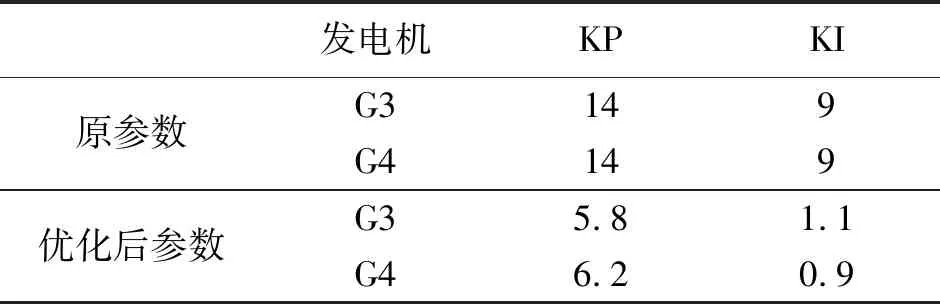
表2 机组调速器参数

G3、G4发电机调速器采用优化后的PI参数，其他条件不变，模拟相同负荷阶跃扰动，系统频率曲线如图5所示。

图5 参数优化后负荷扰动频率曲线

当G3、G4发电机调速器采用优化后的PI参数，相同负荷扰动下系统频率振荡模态几乎不变，阻尼比从-0.12提高到0.13，超低频振荡得到了有效抑制，系统小干扰稳定性提升。

5.2 接地短路故障

仿真EPRI 36节点系统BUS20至BUS22交流线1 s时刻发生三相接地短路故障，1.1 s时刻切除故障线路。

G3、G4发电机调速器分别采用原PI参数和优化后PI参数的系统频率曲线如图6所示。从中可以看出，三相接地短路故障时，G3、G4发电机调速器采用原PI参数时，发生超低频振荡；采用优化后PI参数，超低频振荡得到有效抑制。

由表3可知，G3、G4发电机调速器采用优化后的PI参数可有效提升系统阻尼比，同时说明所提出的水电机组调速器PI参数协调优化方法针对不同扰动类型引发的超低频振荡均能够抑制，具有较强的鲁棒性。

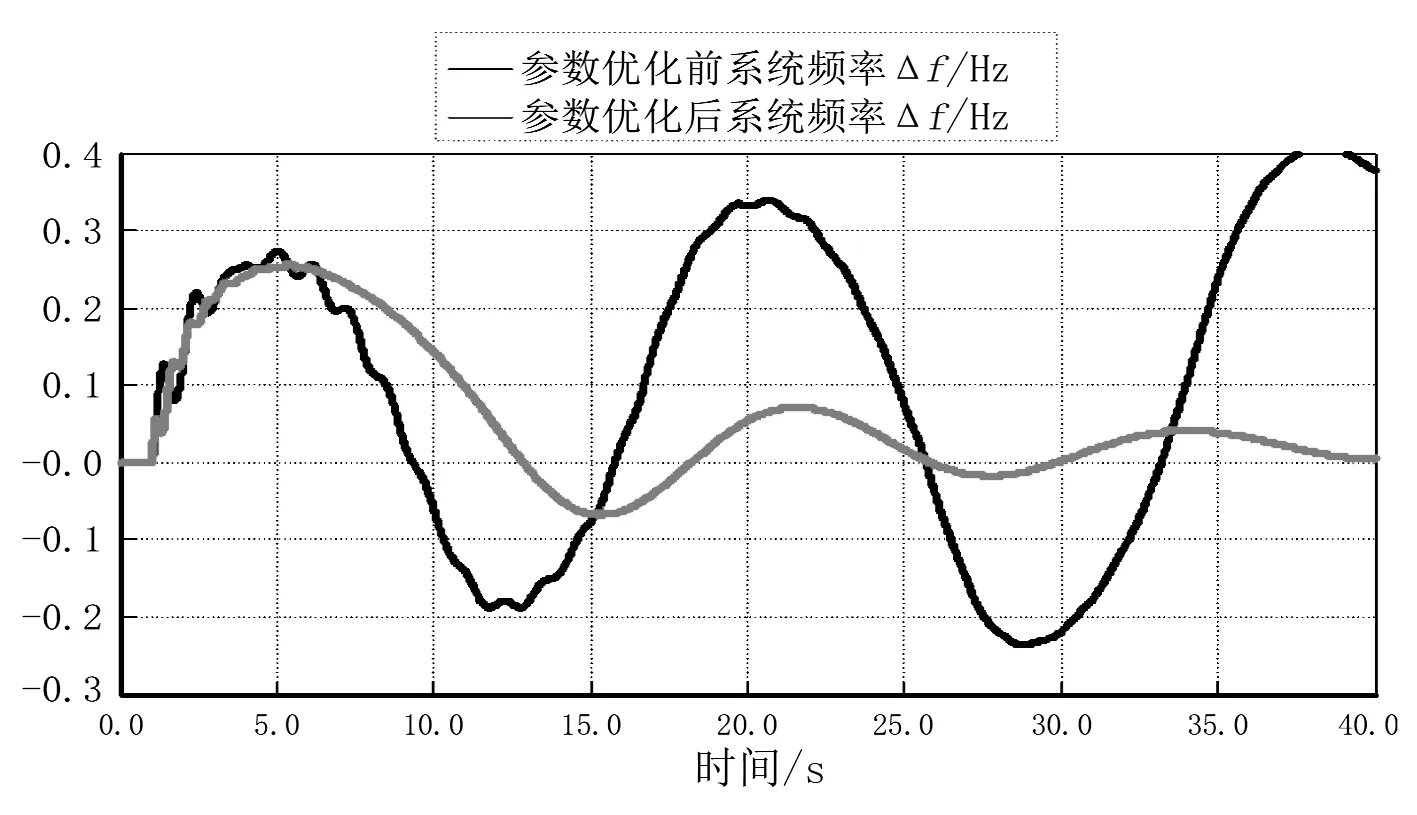
图6 三相接地短路故障时系统频率曲线

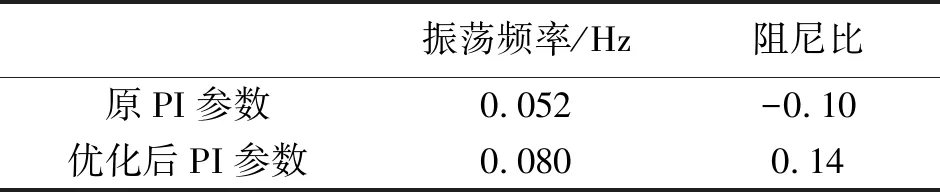
振荡频率/Hz阻尼比原PI参数0.052-0.10优化后PI参数0.0800.14

6 结 语

前面分析了四川电网超低频振荡产生机理，并基于最小二乘法实现了在线拟合发电机机械转矩阻尼系数。当拟合得到的发电机机械转矩阻尼系数为负时，该机组对超低频振荡的贡献度大，可认为是引发超低频振荡的振荡源。为抑制超低频振荡，提出一种水电机组调速PI参数协调优化方法，并将状态子空间辨识算法和改进粒子群算法用于参数优化设计。采用所提方法可准确评估机组对超低频振荡的贡献度，有效抑制超低频振荡。