基于增强CNN模型的手写字体图像识别*

李忠海，王崇瑶，宋智钦，徐 蕾

（1.沈阳航空航天大学自动化学院，沈阳 110136；2.武警工程大学，西安 710000）

0 引言

手写汉字的识别问题一直是图像处理与模式识别研究领域的难点之一。传统的识别方法如最近邻算法［1］、支持向量机、神经网络［2］等，解决复杂分类问题及数学函数表示能力和网络的泛化能力有限，不能达到高识别精度的需求，随着科技的发展和研究，CNN的出现解决了这个问题。它最初由美国学者Cun［3］等提出，是一种层与层之间局部连接的神经网络。文献［4］通过降低C5层的特征图改进了卷积神经网络模型，提高了识别速度；文献［5］提出通过改进激活函数来改变卷积神经网络的性能，提高了识别率。文献［6］提出了基于频度统计生成相似子集，提取训练样本中的梯度特征，改进了识别率和速度。

在此基础上，本文先将原有的图像用高阶差分法进行增强处理，增加汉字的全局特征，然后在原始的LeNet-5结构的基础上，将前两层的激活函数改为ReLu函数，并且去掉C5层以及F6层，通过增加输出层的神经元数来增加汉字的识别率。

1 原始的LeNet-5识别网络

最初LeNet-5是用于手写数字识别的，输出的类别数目为10，但是手写汉字的识别与手写数字识别相比，需分类的类别数目要多很多。除了10个数字外，大约还有3 000多个常见的汉字。原有的LeNet-5网络已经不能满足汉字识别需要了，因此对识别数字的LeNet-5网络进行了改进。

卷积神经网络LeNet-5的结构如图1所示。输入数字的图像要经过大小归一化，神经网络的每一个神经元的输入均来自于前一层的一个局部邻域，并被加上由一组权值决定的权重。提取的这些特征在下一层结合形成更高一级的特征。同一特征图的神经元共享相同的一组权值，次抽样层对上一层进行平均。

图1 LeNet-5结构

卷积神经网络LeNet-5不包括输入，由7层组成，每一层都包括可训练的参数（权值）。该网络的输入是32*32的图像，其中C层是由卷积层神经元组成的网络层，S层是由次抽样层神经元组成的网络层。网络层F6，包括84个神经元，与网络层C5进行全连接。最后，输出层有10个神经元，是由径向基函数单元（RBF）组成，输出层的每个神经元对应一个字符类别。RBF单元的输出Y的计算方法如式（1）所示:

2 增强CNN网络模型

由于原始的LetNet-5网络识别类数少，不能满足识别手写汉字的需要；加上手写汉字存在书写不规范，扫描图像不清晰且存在较大的噪声，难以识别。基于此本文提出了增强CNN网络模型来增加手写汉字的识别率。现对原始的LeNet-5网络进行了改进:

1）由于汉字识别的种类多，训练样本集数据量大，用原始LeNet5网络中的激励函数会出现过拟合现象，现将ReLu函数作为网络前两层的激励函数，能够有效防止训练数据出现过拟合现象，输出层的激活函数仍用softmax。

2）为了得到较高的识别率，则需要更多的特征信息。现将CNN网络的C5层以及F6层去掉，与输出层的神经元进行全连接，来保留汉字的局部和全局特征，增加汉字的识别率。

增强CNN网络模型如图2所示:

图2 增强CNN网络模型

由图2可知，增强CNN网络模型只有5层，模型的层数减少了，这样训练时间也会相应地缩短，同时由于改进后的网络依旧是卷积层和采样层交替出现，所以改进的网络仍保留了图像对位移、缩放和扭曲的不变性和良好鲁棒性的优点。

3 汉字图像的增强处理

在此对输入的汉字图像进行增强处理，以减少特征提取的干扰。本文摒弃了传统的增强算法，引进了五阶滤波模板，提出高阶差分增强算法，用于对输入汉字图像进行增强。

3.1 五阶差分滤波器模板系数的推导

依据偏微分理论在图像处理中的原理［9］，将图像进行离散化，图像微分可用差分近似实现，即用离散差分方程近似代替导数方程。

假设滤波器模板大小为五阶，取为5×5的方阵，滤波系数用Y（i，j）表示，像素的系数根据位置记录，中心点的滤波器系数值记为Y（0，0），5×5滤波器模板表示如下:

四阶差分滤波实现方法是利用五阶滤波器与图像进行卷积运算，一般来说对大小为M×N的图像f（x，y）使用m×n滤波器实现图像滤波的计算公式为:

其中，a=（M-1）/2，b=（N-1）/2，Y （i，j） 是滤波器系数，f（x，y）是图像像素值。随着滤波器在图像f（x，y）中的移动，将计算出新的图像像素值f（x，y）。

由于离散差分方程来近似代替导数方程，可知有如下公式:

进一步可知:

由于二维离散图像进行差分运算时，要确定运算方向。本文采用先前向差分后后项差分，即对图像f（x，y）先做前向差分，当下一次前向差分没有离散像素点时做后项差分。因此，本文只需研究水平（0°和 180°）、45°（225°） 对角、垂直（90°和 270°）、135°（315°）对角4个方向的滤波器模板系数。定义Δnkαf（x，y）为图像f（x，y）在kα方向上的n阶差分，其中 α=45°，k=0，1，2，3。

3.1.1 水平方向的滤波器模板系数推导

当k=0，n=4时，f（x，y）的四阶差分表达式为:

由式（10）可知:差分方程的系数依次为1、-4、6、-4、1。将这5个系数分别作为滤波器系数值，记Y（-2，0）=1，Y（-1，0）=-4，Y（0，0）=6，Y（1，0）=-4，Y（2，0）=1。

3.1.2 45°对角方向的滤波器模板系数推导

由式（11）可知:差分方程的系数依次为1、-4、6、-4、1。将这5个系数分别作为滤波器系数值，记Y（-2，-2）=1，Y（-1，-1）=-4，Y（0，0）=6，Y（1，1）=-4，Y（2，2）=1。

3.1.3 垂直方向的滤波器模板系数推导

当k=2，n=4时，即f（x，y）的差分表达式为:

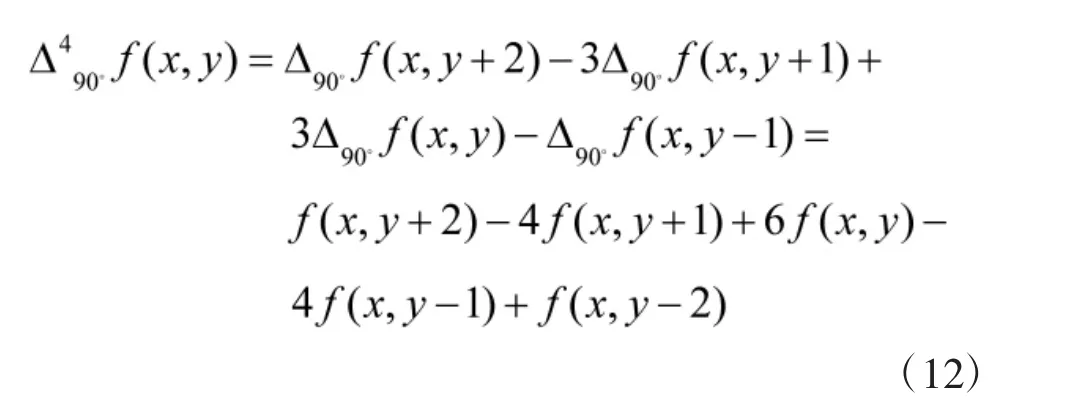
由式（12）可知:差分方程的系数依次为1、-4、6、-4、1。将这5个系数分别作为滤波器系数值，记Y（0，-2）=1，Y（0，-1）=-4，Y（0，0）=6，Y（0，1）=-4，Y（0，2）=1。

3.1.4 135°对角方向的滤波器模板系数推导

当k=3，n=4时，即f（x，y）的差分表达式为:

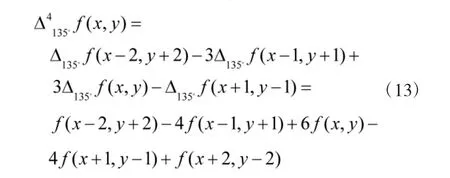
由式（13）可知:差分方程的系数依次为1、-4、6、-4、1。将这5个系数分别作为滤波器系数值，记Y（-2，2）=1，Y（-1，1）=-4，Y（0，0）=6，Y（1，-1）=-4，Y（2，-2）=1。

陪同亲属从柳絮、杨絮纷飞的城市一路开车到达肿瘤医院，路上甚至得知亲人生病后很长时间都沉浸在担心与焦虑里，偶然抬头看到流苏花的那一刻，心里觉得松了一口气，之后留意到每个角落里都热烈生长的植物，心里也愉快了些，寻味到一种“人间四月芳菲尽，山寺桃花始盛开”的意境。再观看每一位穿梭在我身边的人，虽然行色匆匆不曾驻足，却也是面目如素，没有预设中的“悲戚”。在CT室外看到大家都在讨论显影水多么难喝时，我觉得自己此前“谈癌色变”的紧张都显得多余，紧张兮兮、一直面有难色的我在人群里才是最不正常的存在。

综上所述:四阶差分方程4个方向的滤波器模板系数已经分别求出。

将上述4个方向的模板进行线性组合，可得出4个方向的五阶滤波器模板如图3所示:

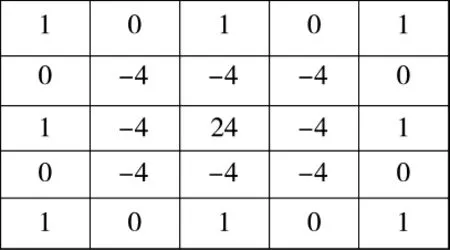
图3 五阶滤波器模板

将4个五阶滤波器模板进行线性组合，则图像边缘增强后的新图像表达式为:

4 实验结果及分析

为了获取较真实的实验数据，增加算法的说服性，本文采用中科院自动化研究所和模式识别国家重点实验室联合建立的手写字体数据集CASIA-HWDB1.1进行实验验证。它包括3 755个一级手写汉字以及171个数字和符号，其中手写汉字的总样本容量为1 121 749个。在本文中实验数据集从中选择了306个汉字所对应的30 600个样本，每个手写汉字包括300个手写体样本。本文将每个汉字的290个样本拿来训练，剩下的10个样本拿来测试。训练样本图片的大小为69*69。部分手写汉字的训练样本如图4所示。

图4 训练样本

4.1 迭代次数与训练样本正确率的关系

表1 迭代次数与训练样本正确率的关系

如表1所示，随着训练样本的迭代次数增多，训练样本的正确率也在提升。但是，当迭代次数达到一定的数目时，训练样本的正确率达到100%，继续训练，测试样本的错误率在下降，并且趋近平稳，基本上没有过训练的情况。这说明ReLu激活函数很好地补救了训练数据出现过拟合的现象，同时也体现了改进后的CNN网络良好的性能。

4.2 增强处理与误识别率的关系

为了分析经过图像增强处理后，手写汉字误识别率的大小和本文算法的优越性，将本文算法与目前几种常用的识别方法进行对比，对比数据如表2所示:

从表2中可以看出，早期的识别方法误识别率较大，高达15%；而CNN识别方法效果较好，误识别率为0.98%。通过CNN算法与本文增强CNN算法对比，可以看出经过高阶差分增强处理的CNN算法误识别率更低，仅为0.5%。相比较而言，本文算法比未增强处理的CNN算法识别率提高了0.48%。进一步表明本文算法在手写汉字识别方面占据一定的优势。

4.3 手写汉字识别效果测试

实验识别所用卷积神经网络模型参数的设定:

1）输入图像为69*69大小，图像增强模板用的是五阶滤波器模板如图3所示。

2）卷积层为6个20*20的模板，池化层采用2*2的模板。

识别效果如图5所示:

从测试的汉字来看，本文算法的识别度比较高，效果比较好。

5 结论

本文将输入图像用高阶差分法进行图像增强处理，然后在原始的LeNet-5结构的基础上，将前两层的激活函数改为ReLu函数，并且通过增加输出神经元的个数，来增加字体的识别率。经过数据分析，ReLu激活函数很好地补救了训练数据出现过拟合的现象；增强处理比未增强处理的CNN算法识别率提高了0.48%。实验证明，手写汉字随着训练样本数据的增大，识别率也在逐渐增加，高达99.5%。可见，本文算法在手写汉字识别方面有一定的优势。但是，如何能够在军事领域应用识别，准确识别出被遮挡或者未写完的汉字将是下一步研究的课题和方向。