气固绝缘系统电场模型的建立与求解方法

李乃一,彭宗仁

(1.国网浙江省电力有限公司电力科学研究院,310014,杭州;2.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安)

针对气体绝缘开关/输电线路(GIS/L)、套管等电力设备进行绝缘结构设计的先决条件是合理计算各种电压形式下气固绝缘系统的电场分布。文献及工程设计中,一般通过求解电流场获得直流电场分布[1-2],除电流连续性方程外,如何合理地给出另一个电流密度与场强的单独对应关系(如欧姆定律)是计算结果准确与否的关键。在很多情况下,电流密度很难通过这种简单的对应关系来表征,事实上电流密度与载流子类型、来源以及动态变化方式都有一定关系。气体电流密度与场强呈现出类似于欧姆定律的变化仅在极小场强下存在,随后电流密度将达到饱和并在一定场强范围内保持不变,仅当场强超过某一限值后,电极发射电子(正离子碰撞阴极、光电效应等)在强电场作用下加速冲击分子,使其进一步电离,电流密度才又再度随场强的增加而上升,如图1所示。

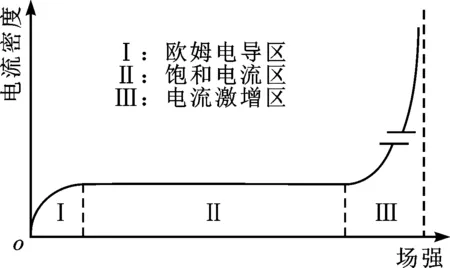
图1 气体电流密度与场强的关系

对于弱电离气体,气体电流是正、负离子在库仑力作用下的漂移运动形成的。Weigart等对SF6气体的自然电离率以及离子的迁移率、扩散系数、复合系数进行了较为全面的测量,并给出了相应的运动方程[3]。Volpov建议将文献[3]运动方程应用到气固绝缘系统的电场建模中以提高直流电场计算的准确性[1];文献[4-5]建立了直流电压下气固绝缘系统的电场模型,计算得到的柱式绝缘子表面电位分布与测量结果吻合较好;文献[6]在进行类似工作时利用电力线将绝缘子表面划分为若干微单元来计算电流密度,但该方法要求对求解域进行分区迭代,实现过程比较繁琐。文献[7]实测了空气中的正、负离子浓度,并据此对空气等效电导率进行了估算。尽管固体介质内部自由电荷的运动方式与气体介质中类似,但由于载流子来源涉及电极注入、电荷脱陷、杂质离子解离等过程,因此相应的边界条件更为复杂[8-9]。文献[10]的测试结果表明,弱电场下,气体绝缘电力设备中常用的双酚A二缩水甘油醚型环氧树脂的电导电流密度与场强近似呈线性关系。

目前,普遍采用恒定电流场方法计算气固绝缘系统的直流电场。尽管已经认识到该方法在某些情况下计算误差很大,并提出了一些符合实际物理过程的计算方案,但仍然缺少系统性的建模、求解及测量验证工作。

本文基于气固绝缘系统中的电荷驰豫过程,建立了复合绝缘系统的电场模型和弱电离气体的电导模型,给出了模型的求解方法,并进行了算例验证。本文研究结果可为直流气体绝缘设备结构设计及直流电压下绝缘子表面电荷积聚特性研究提供电场仿真方法。

1 模型的建立

1.1 复合绝缘系统的电场模型

1.1.1 静电场基本方程 根据麦克斯韦方程组,在变化的电磁场中引入矢量(磁失)位函数A和标量(电)位函数φ后,电场强度E可表示为

(1)

式中:t为时间。

由于交流电力设备不同电极间的电位差随时间的变化较为缓慢,同时电极间的距离远小于相应电磁场的特征波长,因此任一瞬间的电场可以近似看作静电场,于是有

E=-φ

(2)

根据高斯定律,场强与体电荷密度ρ的关系为

·(εE)=ρ

(3)

式中:ε为介电常数。

将式(3)用于两种介质的分界面,即可建立场强与界面电荷密度σ的关系

n·(ε1E1-ε2E2)=σ

(4)

式中:n为介质2指向介质1的法向单位向量;ε1为介质1的介电常数;ε2为介质2的介电常数;E1为介质1侧的场强;E2为介质2侧的场强。

固体绝缘材料的本征时间常数(介电常数与体积电导率之比)通常可达103s以上。根据界面极化理论,工频电压下缓慢的界面极化过程使得复合绝缘系统内部的电荷量几乎为0,于是有

·(εE)=0

(5)

由式(2)(5)可计算工频电场分布。由于忽略感应电场后,冲击电压波形有效频率远大于50 Hz,因此冲击电压下任意时刻的电场分布也可近似采用与工频电压下相同的方法进行计算。

1.1.2 电流场的基本方程 电流密度J与体电荷密度的关系满足电流连续性方程

(6)

将式(3)代入式(6)后,可建立电流密度与场强的关系如下

(7)

若电流密度符合欧姆定律

J=γE

(8)

式中:γ为体积电导率。结合式(7)(8),有

(9)

由式(2)(9)即可求解直流电场分布。

1.1.3 固体介质内部的体电荷密度方程 结合式(3)(8),有

J··J=ρ

(10)

将式(6)代入式(10)后,即可建立体电荷密度的暂态方程

(11)

式(11)反映了电流与电荷的关系,即电流在ε/γ梯度方向上存在分量时将产生电荷。需要指出的是,自由电荷的存在会使介质内部各个位置上载流子的浓度以及迁移率发生变化,严格来说此时体积电导率的概念已不再适用于表征介质的导电性(或者说电导率无法测量),而一般所采用的电导(阻)率只是一种宏观上的平均值。

工程绝缘材料的介电常数在电力设备常见的温度和场强范围内通常变化较小,故可近似看作常数。体积电导率受温度和场强的影响相对较大,且影响程度对绝缘材料本身及填料的特性均十分敏感。例如,双酚A二缩水甘油醚型环氧树脂/Al2O3复合材料的工频介电常数在0～120 ℃内的变化一般不超过10%,体积电导率在0～100 ℃内会出现2个数量级左右的变化,而场强则需要超过104V/mm后才会对体积电导率的数量级产生影响[11]。对于添加ZnO压敏材料或SiC等非氧化物填料的聚合物复合材料来说,体积电导率在100～1 000 V/mm内便会出现2～3个数量级的变化[12]。

忽略介电常数的变化,将式(11)中的梯度算子展开

γ

(12)

将式(8)(11)(12)相结合,即得到与场强有关的体电荷密度的暂态方程

(13)

1.1.4 气固界面上的电荷密度方程 气体绝缘设备涉及到的介质分界面主要为气固界面,另外还有少量固固界面,这两类分界面上的电荷交换方式一致。下面以气固界面为例,给出表面电荷密度方程。

研究表明,工程绝缘材料表面存在本征导电层或由表面状态(如水分吸收、化学反应等)引起的导电层,厚度为亚微米级,即使是在表面积污或涂覆防污、防雨闪涂料的情况下,厚度通常也只有几百微米[13-14]。尺度远小于材料本身的表面导电层给绝缘子电场建模(网格剖分)及求解造成了一定困难。

Volpov从电流连续性方程出发,推导了忽略导电层厚度的表面电荷密度的暂态方程[1]

(14)

式中:J1n为固体侧(气体侧)的法向电流密度;J2n为气体侧(固体侧)的法向电流密度;Jτ为切向线电流源;n为固体侧(气体侧)指向气体侧(固体侧)的法向方向;τ为表面切向方向。

若切向电流同样符合欧姆定律,于是有

(15)

式中:Eτ为表面切向场强;χ为表面电导率

χ=γd

(16)

其中d为导电层厚度。

式(15)建立了表面电荷密度与分界面两侧的电流密度、表面切向场强的关系。据此利用式(6)计算表面电荷密度,并通过式(4)将其作为电场模型的一个边界条件,从而简化绝缘子表面的建模和求解。需要特别说明的是,若导电层仅在绝缘子表面部分覆盖或体积电导率不连续,则需在相邻导电层间添加点电荷密度方程,或者将各个部分的导电层分别建模,以反映分界面上的电荷积聚效应。

表面电荷在工频和冲击电压下的积聚方式较为特殊,根据全电流定律,切向线电流源可表示为

Jτ=χEτ+idωεEτ

(17)

式中:ω为外部电场随时间变化的角频率;χEτ为阻性电流项;dωεEτ为容性电流项。

当绝缘子表面干燥、清洁,表面电导率较小时,式(17)的阻性电流远小于容性电流,建立界面极化时长远大于电场变化周期,因此表面几乎不发生电荷积聚,电场为纯容性;当表面积污、积水,表面电导率较大时,阻性电流接近或超过容性电流,此时会在短时间内部分或完全建立界面极化,产生随时间周期变化的表面电荷。

值得注意的是,上述规律对于固、固界面来说同样存在:工程绝缘材料一般为容性材料添加半导电填料的聚合物,复合材料体积电导率随场强的变化幅度很大(γ∝Eα,α为系数),据此可在套管、电缆附件等电力设备的局部强电场区域内应用该类材料,以起到利用界面电荷均匀电场的作用。

1.1.5 边界条件 电极表面电位满足Dirichlet条件,表达式为

φ=u(t)

(18)

式中:u(t)为电压。

悬浮电位电极的表面净电荷为0,于是有

(19)

式中:n为悬浮电位电极表面的法向单位矢量;S为悬浮电位电极表面。

1.1.6 直流电场的求解方法 直流电场的建立过程是电场由容性分布转变为阻性(电流)分布的过程,完成的标志是介质分界面两侧电流密度的法向分量相等,且介质内部电流密度的散度为0。一方面,由电流连续性方程建立场强与电流密度的关系后,若可将电流密度表示为另一个场强的单变量函数,联立两者即可求得电流密度分布以及相应的电场分布,即恒定电流场的求解过程。

另一方面,从电荷变化的角度来说,直流电场的建立过程也是场域内电荷积聚逐渐饱和的过程,因此电场可以看作是由外施电压瞬时建立的电场(包括几何电场和极化电荷建立的感应电场,后者的建立时间忽略不计)与自由电荷缓慢建立的电场在空间中的叠加。在已知自由电荷分布的情况下,任一瞬间的电场均可由泊松方程建立场强与电荷密度的关系进行求解。

可见,直流电场的正向求解方法应是构建自由电荷密度方程并实时计算电荷所产生的泊松场分布。与求解电流场相比,该方法可直接获得体电荷和界面电荷密度分布的暂态变化过程,无需对计算结果进行后处理(电流场计算完毕后,可分别根据式(10)(4)间接获得体电荷和界面电荷的密度分布),同时还可将各种电压形式下的计算统一起来,即采用同一微分方程组求解各种电压形式下的电场分布,从而简化电场建模。

1.2 弱电离气体的电导模型

1.2.1 基本方程 当气体中存在离子、电子以及其他带电粒子时,本身会具有导电性。这些载流子通常是由气体分子在强电场下通过碰撞电离或高能宇宙射线等辐射电离产生。本文在建立气体电导模型时,忽略阴极电子发射等其他与暗电流形成有关的电离因素,仅考虑气体分子的自然电离,相应的载流子类型为成对出现的正、负离子。

在电场建立过程中,正、负离子在库仑力作用下沿电力线作迁移运动,其中一部分在运动过程中发生复合形成分子,另一部分最终抵达电极表面,在与电极发生碰撞后捕获或释放电子形成分子并重新返回气体中。这部分抵达电极表面的离子在气体间隙中的运动形成了弱电离气体中的电流,此外离子在局部浓度差作用下的热扩散运动也会产生电流。

气体中正、负离子迁移、扩散运动形成的离子流密度I±的表达式为

I±=±μ±ρ±E-D±ρ±

(20)

式中:μ±为正、负离子迁移率;D±为正、负离子扩散系数,在弱电场下可由Einstein方程求得

(21)

其中,kB为玻耳兹曼常数,kB=1.38×10-23J/K,T为温度,e为元电荷,e=16×10-19C。

正、负离子流密度之差即为气体电流密度

J=I+-I-=

(μ+ρ++μ-ρ-)E-(D+ρ+-D-ρ-)

(22)

正、负电荷密度与离子流密度满足电荷连续性方程

(23)

式中:dN/dt为气体电离率;k为离子复合系数,Langevin类型的k可表示为

(24)

对于空气,式(24)仅当气压大于0.3 MPa时适用。

将式(20)代入式(23),有

(25)

根据式(3),电荷密度满足

·(εE)=ρ+-ρ-

(26)

联立式(2)(25)(26),即可求得气体介质中的电位、场强以及正、负离子浓度的分布。

1.2.2 气体电流密度与场强的关系 正、负离子的来源与去向可表示为

(27)

式中:Ns、Nf、Nd分别为生成、复合和抵达电极的离子数。

式(27)表明,新生成离子对气体电导的贡献取决于其单独存在于气体中的时间。对于一对充气无限大平板电极来说,当平均电场较小时,绝大多数的正、负离子在抵达电极前已发生复合,两者均为离子平衡态浓度

(28)

忽略离子的扩散运动,根据式(22),气隙中部的电流密度可表示为

(29)

式(29)表明,弱电场下J与E的关系符合欧姆定律。

当E较大时,大部分正、负离子都已抵达相应的电极,故电流密度只与电极距离和电离率有关

(30)

将式(29)(30)中的dN/dt分别作为单位时间内发生复合和抵达电极离子的浓度代入式(27),有

(31)

根据式(22),计算不同场强下间距1 m的平板电极间空气和SF6气体时的电流密度,并与式(31)的计算结果进行对比,结果如图2所示。

0.1 MPa,空气:dN/dt=10 (cm3·s)-1,μ±=1.6 cm2/(V·s),k=2×10-6 cm3/s,T=20 ℃;0.1 MPa,SF6:dN/dt=10 (cm3·s)-1,μ±=0.36 cm2/(V·s),k=1.7×10-6 cm3/s,T=20 ℃;0.4 MPa,SF6:dN/dt=32 (cm3·s)-1,μ±=0.13 cm2/(V·s),k=6×10-7 cm3/s,T=20 ℃图2 平板电极间气体电流密度随场强的变化情况

从图2可以看到:气体电流密度随场强的增加先快速增加,随后增加速度逐渐减小,并最终达到饱和;饱和电流密度随气体电离率的增大而增大,饱和所需的外部场强也随之增大。两组结果的趋势基本吻合,但数值存在一定的偏差,原因是,式(31)的推导过程假设了电极间的均匀电场保持不变,同时忽略了离子热扩散所形成的电流,而式(25)和(26)的计算结果则包含空间电荷分布以及离子扩散运动对电场分布的影响。

由此可见,基于欧姆定律并采用恒定电阻率线性描述气体介质中电流密度与场强的关系显然不够准确。电流密度饱和后不再随场强增大而进一步增大的现象说明,在一定范围内,电场本身不能使气体发生电离,增大场强只能让更多的离子抵达电极表面参与电导过程。

1.2.3 边界条件 气、固界面上的电荷密度采用开放边界条件,即离子流(式(20))流入边界上电荷密度为0,流出边界上离子流密度扩散项的法向分量为0

(32)

1.2.4 基本参数 文献[3,7,15-21]给出的空气和SF6气体的dN/dt、μ±、k的测量结果汇总于表1。

从表1可见,dN/dt与辐射强度和气压成正比、与腔体大小成反比,这主要是由于有效电离受宇宙射线能影响及腔体壁二次辐射效应所引起的。SF6气体中的μ±、k与气压成反比,这与高气压下簇离子的形成有关。

2 模型的求解

2.1 对流扩散方程的使用限制

电场模型中的对流扩散方程(式(25))存在一些数值计算方面的限制。

(1)采用Galerkin法(COMSOL Multiphysics的内置场域离散方法)对求解域进行离散时,若对流扩散方程包含非常数的源项或其数值解在Dirichlet边界上的梯度较大时,一旦Péclet数大于1(扩散项数值较小),方程的数值解便会在局部出现不同程度的振荡。由于式(25)包含了非常数的离子复合项,同时空间电荷密度在电极附近梯度较大,且对于气体而言,D/μ一般远小于1 V,故式(20)等号右侧的迁移项(第1项)远大于扩散项(第2项),因此上述现象极有可能发生。一般来说,当存在扩散项时,方程的数值稳定性便主要取决于单元分辨率,因此在相应区域内增加单元密度可显著改善数值振荡现象,但该方法同时也会导致单元数的大幅增加,使其可行性相对较差。另外,从Péclet数出发,可通过添加数值扩散项提高方程数值稳定性。Comsol内部可添加的数值扩散项有各项同性扩散项、流线扩散项和侧风扩散项,采用的有限元计算方法包括上流Petrov-Galerkin法和Galerkin最小二乘法。

表1 文献中空气和SF6气体dN/dt、μ±、k的测量结果

(2)如果对流扩散方程中的各个变量在数量级上差别过大(对于式(25),当外施电压较高且电荷密度(10-15～10-14)和场强(106～107)的数量级差别较大)时,方程在求解过程中会产生病态矩阵,导致计算收敛缓慢或者难以收敛。若事先已知各个变量的数量级,可在求解前对其进行缩放处理来提高方程的收敛性。在求解非线性问题时,变量的缩放比例需在每次迭代后根据当前结果重新计算得到。当变量本身在求解域内变化较大时,该方法的收效会大大降低。

(3)对于结构复杂、场域较大(开放空间)、单元数较多的仿真模型来说,对流扩散方程的收敛性较差。

2.2 电场模型在COMSOL Multiphysics中的求解

电场计算所需的全套微分方程可采用多物理场有限元软件COMSOL Multiphysics(v4.3a)构建并求解,在Comsol中模块化的实现方法如表2所示,具体说明如下。

(1)“静电”模块用于建立介质内部的场强方程。若介质内部自由电荷密度为0(固体介质内部恒温,气体介质采用饱和电流密度),则在子模块“电荷守恒”中添加相应的介质区域,反之应将其添加到子模块“空间电荷密度”中,并耦合相应的电荷密度。采用子模块“电位”设置高压和接地电极的表面电位,采用子模块“悬浮电位”设置悬浮电位电极的表面电位。初始时刻求解域内所有位置上的场强均为0。

(2)“域常微分方程和微分代数方程”模块用于建立固体介质内部的体电荷密度方程。通过自定义随温度变化的固体介质体积电导率耦合相应的温度场分布。初始时刻求解域内所有位置上的电荷密度及随时间的变化均为0。

(3)“稀物质传递”模块用于建立气体介质内部正、负离子的电荷密度方程。采用子模块“开放边界”设置气体介质边界上的电荷密度。初始时刻求解域内所有位置上的电荷密度均为气体平衡态浓度,随时间的变化同样为0。

(4)“边界常微分方程和微分代数方程”模块用于建立介质分界面上的界面电荷密度方程。在“静电”的子模块“表面电荷密度”中添加相应的分界面,并耦合界面电荷密度。初始时刻分界面所有位置上的电荷密度及随时间的变化均为0。

此外,工频电场和恒定电流场可以分别使用“静电”和“电流”模块进行求解。

其他相关的说明包括下面内容。①建模与剖分。采用SolidWorks软件建模并导入Comsol中进行网格划分,其中2维模型采用三角形单元,3维模型采用四面体单元,对局部关注区域(如电极附近、绝缘子表面等)的网格进行加密处理。当采用弱电离气体电导模型时,需对整个气体介质区域进行网格加密来抑制数值振荡。②求解模式。工频电场采用稳态求解,直流电场既可求稳态解也可求暂态解。通常情况下,时域求解的收敛性好于稳态求解,前者在求解时需要添加一个误差终止条件作为结束判据。③求解器。非线性算法为阻尼牛顿法,时域算法根据情况选用向后差分法(BDF)或广义α法。

表2 电场模型在COMSOL Multiphysics中的构建方法

3 模型的验证

制作了常用于GIS/L的柱式绝缘子实验模型,测量了直流电压下绝缘子表面的电位分布,并与数值计算结果进行了对比。

3.1 实验模型及其制作

实验采用的柱式绝缘子模型的几何尺寸:环氧浇注试品为直径40 mm、高90 mm的圆柱;嵌件为直径20 mm、高35 mm的铝块,端部为半径5 mm的圆角;铝电极为直径80 mm、厚10 mm的圆盘,边缘为180°的圆弧。嵌件和电极均经过抛光处理以减少表面微放电的发生。环氧浇注试品由双酚A二缩水甘油醚型环氧树脂与固化剂(甲基六氢邻苯二甲酸酐)和促进剂(N,N-二甲基苄胺)混合搅拌均匀并进行真空脱气处理后,倒入事先用丙酮清洗并涂有脱模剂的不锈钢模具中(嵌件同样已提前用丙酮擦拭并固定在模具两端),通过阶梯升温固化而成。试品制备完毕后,用细砂纸打磨以除去表面残留的脱模剂,将两个电极通过螺栓分别固定在试品两端。最后,将绝缘子模型浸没在无水乙醇中进行超声波清洗,以清除制作过程中表面吸附的污染物。柱式绝缘子模型如图3所示。

(a)示意图 (b)实物图图3 柱式绝缘子实验模型

3.2 表面电位测量系统与方法

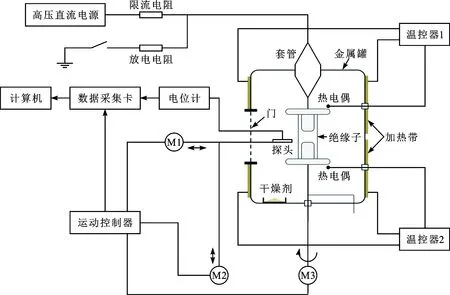
图4 表面电位测试系统示意图

(1)测量系统。表面电位测量在一个直径25 cm、高40 cm的金属罐内进行。将固定有绝缘子模型的粗铝棒由罐底伸出,并连接在一个电动旋转台上来控制绝缘子旋转,如图4所示。直流电源由多波形信号发生器(RIGOL,DG3101A)输入到高压功率放大器(Trek,40/15-H-CE,输出电压0～40 kV DC/AC)后,通过一体式套管进入罐体内部。上电极通过顶部带滚珠的铝棒伸入进线套管内部与其内芯接触(在不影响绝缘子旋转的前提下保证电位传递),下电极通过铝棒与接地罐体相连。

采用两个电动滑台控制固定在PTFE支架上的Kelvin探头(Trek,3455ET,最高工作温度为100 ℃,响应速度小于200 μs,噪声小于20 mV)穿过罐体侧门靠近绝缘子模型(探头端部距试品表面约3 mm)并反复做纵向运动,配合底部旋转台可对试品表面进行探测,该过程由可编程运动控制器控制完成。电压信号经静电电位计(Trek,341B,测量范围为0～20 kV DC/AC)除以1 000后输出,并接入计算机数据采集系统记录其随时间的变化。

罐内温度由两截分别均匀缠绕在罐体上部和下部外壁上的加热带进行调控,外部由隔热棉包裹,加热过程采用PID控制来抑制温度过冲。与上、下加热带相连的两个热电偶被置于与上、下电极相同高度处,以标定相应水平位置上的温度。采用饱和LiCl溶液(干燥剂)将罐内湿度控制在10%～15%。

(2)测量步骤。在常压空气中进行测量,具体步骤为:①将绝缘子模型的上、下电极接地,并置于65 ℃的烘箱中真空干燥约12 h,缓慢降温后取出;②将模型装入实验腔内,上电极经由放电电阻接地后测量,确认试品表面各处无残余电荷存在(电位幅值不超过3 V);③打开温控器加热4 h;④加压2 h后关闭电源,上电极接地后测量。

因探头外壳(其电位与被测信号相等)不能与电极接触,测量无法完全覆盖整个纵向范围,实际探测高度为70 cm。为尽量消除探头运动中加速、减速过程在测量结果位置对应上产生的误差,选取同一运动方向上的测试结果,一次测量共获得736个有效数据。测试时,探头平均移动速度为17.5 cm/s,采样频率为10 Hz,模型旋转间隔为22.5°。

(3)计算方案与参数。建立与实验布置相同的2维轴对称模型,采用本文方法进行计算,将得到的自由电荷密度在试品表面的感应电位值与测量结果进行对比。计算时,环氧浇注材料的相对介电常数根据样片测试结果(测试设备Novocontrol,Concept80)选取20～80 ℃、50 Hz下的平均值4.5,40 ℃(测量温度)时体积电导率为2.2×10-16S/m(测试设备Megger,IDX-300,测试场强2.5 kV/mm),忽略干燥环境下本征表面电导率的影响;空气电离率为20～30 (cm3·s)-1,离子迁移率为1.6 cm2/(V·s),离子复合系数为2×10-6cm3/s;进线套管相对介电常数为6,电导率为10-14S/m。所有的建模及解算工作均在一台Xeon 8×3.30 GHz处理器、192 GB内存的工作站上完成。

3.3 实验及计算结果与讨论

绝缘子模型在40 ℃恒温、不同直流电压下的测量结果与计算结果如图5所示。从中可以看到,计算得到的表面电位分布的整体变化趋势以及各电位峰位置均与测量结果吻合较好。从电荷分布角度看,试品下部始终积聚与下电极符号相同的电荷;试品中上部在电压较低时积聚与上电极符号相反的电荷,电荷量随电压的升高而减小,随后开始积聚同号电荷;在1～20 kV范围内,试品上部异极性电荷峰始终存在,但对整体电位分布的影响程度随着电压的升高逐渐减弱。从图5中可以观察到一个较不规则的实验现象,即试品中、上部的测量结果在正、负极性电压下并不都呈严格的镜像分布:当电压为1 kV时,上部异极性电位峰在正极性电压下的峰值略小于负极性电压;在5 kV时,不对称分布表现的更加明显,负极性电压下的异极性电位峰峰值约为正极性电压下的1.5倍;在10 kV下,负极性电压下原本极性应为负的异极性电位峰极性却为正;正、负极性电压下的感应电位分布在20 kV下基本为镜像分布。上述“异常”现象已通过若干次的复测实验得到了进一步确认。

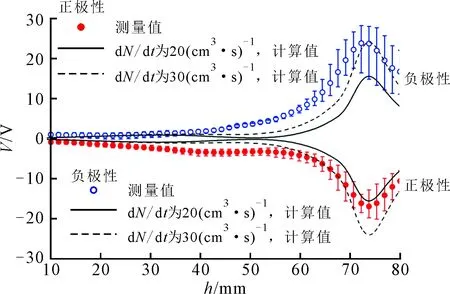
(a)1 kV

(b)5 kV

(c)10 kV

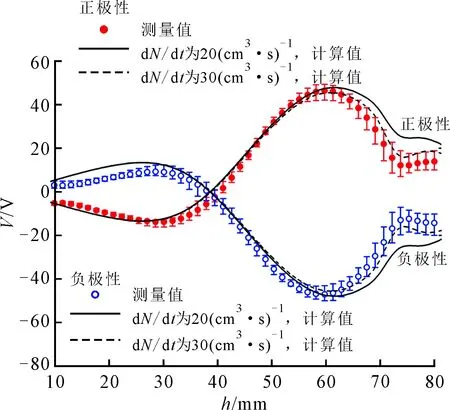
(d)20 kV图5 绝缘子模型表面电位分布随外施电压的变化

关于测量结果在正、负极性电压下不完全对称的现象,从理论计算的角度看(本文忽略了试品表面电导率以及正、负离子迁移率间所可能存在的差异):首先,由于式(17)中的表面电导项·(χEτ)与场强有关,因此该现象不会在试品表面泄漏电流相同(即χ不随电压极性发生变化)的情况下发生,若试品表面电导率与切向场强Eτ成指数关系,面电荷密度σ∝Eτ∂Eτ/∂τ,故表面电导率的影响程度应随宏观场强(电压幅值)的增大而增大,而这与测量结果恰好相反;其次,由于实验腔大部分区域内的气体电流密度在1 kV下便已达到饱和,因此其不应受到离子迁移率的影响;最后,根据式(22),正、负离子扩散系数间的差异会造成正、负极性电压下电荷分布的不同,但该影响对于气体介质来说通常较小。

对比计算结果与测量结果,气体电离率的变化主要影响试品中、上部的计算结果,这与实验现象一致。测量结果在正极性电压下与小电离率下的计算结果较为吻合,在负极性电压下则更接近大电离率下的计算结果。因此,一种可能性较大的原因是,尽管场强较小(本文实验模型上电极表面场强最大值为0.1～2.3 kV/mm(1～20 kV)),但负极性电压下仍存在阴极发射电子的过程。

在绝缘子配置嵌件的情况下,根据上文分析,气体侧电流密度将有所增大。文献[22]在类似实验布置下观察到的0.5 MPa SF6气体中的现象则不明显,这可能是因为SF6气体中电子由于较强的亲和性几乎都附着于气体分子形成负离子的缘故。在配置屏蔽罩(由屏蔽罩表面发出的电力线直接穿过绝缘子表面)的情况下,负离子增多会增加气体侧电流密度,Okabe等测量了0.5 MPa SF6气体中接地屏蔽罩附近的绝缘子表面电位,感应电位在正极性电压(屏蔽罩为阴极,表面最大场强4 kV/mm)下的幅值约为负极性电压下的1/2,该结果佐证了上述观点[23]。另外,文献[24]发现同轴圆柱电极间的0.45 MPa SF6气体在0.3～0.7 kV/mm负极性场强范围内的电流密度较背景电离所形成的电流密度增大了2～3倍,且增大倍数与电极粗糙度无关。文献[25]在PTFE绝缘子模型电极附近布置了针尖作为额外的电离源(电荷来源为强电场下的碰撞电离)后发现,试品表面除电荷迁移区域外,其附近区域的感应电位也有所增大,并认为某些扩散作用会改变电荷的运动方向,但该文没有对测量结果进行反演计算来进一步验证该观点。

4 结 论

(1)建立了基于介质内部和分界面上电荷驰豫过程的复合绝缘系统电场模型。该模型通过构建自由电荷密度方程并实时计算电荷产生的泊松场分布,可获得体电荷和界面电荷密度分布的暂态变化过程,并实现利用同一微分方程组求解各种电压形式下的电场分布。

(2)建立了基于气体自然电离和离子迁移、扩散运动的弱电离气体电导模型,对比柱式绝缘子表面电位测量结果,该模型可表征气体电流密度与场强的非线性关系。

(3)直流电压下,柱式绝缘子配置嵌件时表面主要积聚同号电荷,强电场下则正好相反。负极性电压下的阴极发射电子过程将增大空气侧电流密度,但该现象在SF6气体中不明显。