采用非相关字典学习的滚动轴承故障诊断方法
张志强,孙若斌,徐冠基,杨志勃,陈雪峰
(1.中车青岛四方机车车辆股份有限公司,266000,山东青岛;2.西安交通大学机械工程学院,710049,西安)
滚动轴承是旋转机械重要的支撑部件,也是易损部件,广泛应用于各种大型工业装备中,如风力发电机、航空发动机、高铁动车组等。滚动轴承故障轻则造成装备停机影响运行生产,重则机毁人亡造成灾难性事故。因此,进行滚动轴承早期故障监测诊断是减少运行维护损失、保证设备运行安全的有效途径,具有重要的工程意义[1]。
振动监测是轴承故障诊断最有效的途径之一[2-3]。稀疏表示将振动信号在冗余的波形函数集合(称为过完备字典)中展开,增强了信号的表示能力,具有自适应、对噪声鲁棒性强的优点,适合轴承早期微弱故障特征提取。近几年来,越来越多的研究采用稀疏表示方法分析机械振动信号,并取得了一定的研究成果。如文献[4-5]利用小波字典稀疏表示齿轮箱振动信号,成功匹配出瞬态故障特征成分;文献[6]在压缩感知框架下,从信号集合中学习冗余字典,提取了轴承振动的冲击成分;文献[7]采用K均值奇异值分解训练字典,成功诊断了行星轮系中齿轮的局部和均布式故障。
一个适合于提取故障特征的字典需要满足两个条件:首先字典中原子要与待提取的特征相匹配;另外字典要满足低相关度要求。字典的相关度μ定义为原子间内积绝对值中的最大值。Tropp等证明了只有μ小于某个特定值时,稀疏系数才能由算法成功恢复[8]。从以上研究中可见,固定的参数化解析字典和字典学习方法构造的字典中,原子都与故障特征具有较高的匹配度,但不能满足低相关度要求。传统字典学习方法,如最大似然法[9]、最优方法(MOD)[10]、K-SVD算法[11]等,训练出的字典原子之间具有很强的相关性,不能够表现出信号不同的结构特性,不能确保信号准确稀疏重构,影响了故障特征提取精度。
因而,本文利用文献[12]提出的非相关字典学习算法(INK-SVD)训练低相关性字典,稀疏提取轴承微弱故障特征信号。该方法在K-SVD算法的基础上,加入了解相关的步骤,迭代地选择出字典中的高相关性原子组,并把它们解相关,直到达到给定的相关性,训练出一个具有低相关性的自适应字典。通过仿真分析及故障模拟实验表明,与传统字典学习算法相比,该方法更有利于在强噪声中提取微弱冲击特征,更适合滚动轴承早期的故障诊断。
1 稀疏表示理论
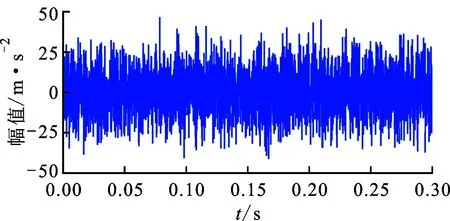
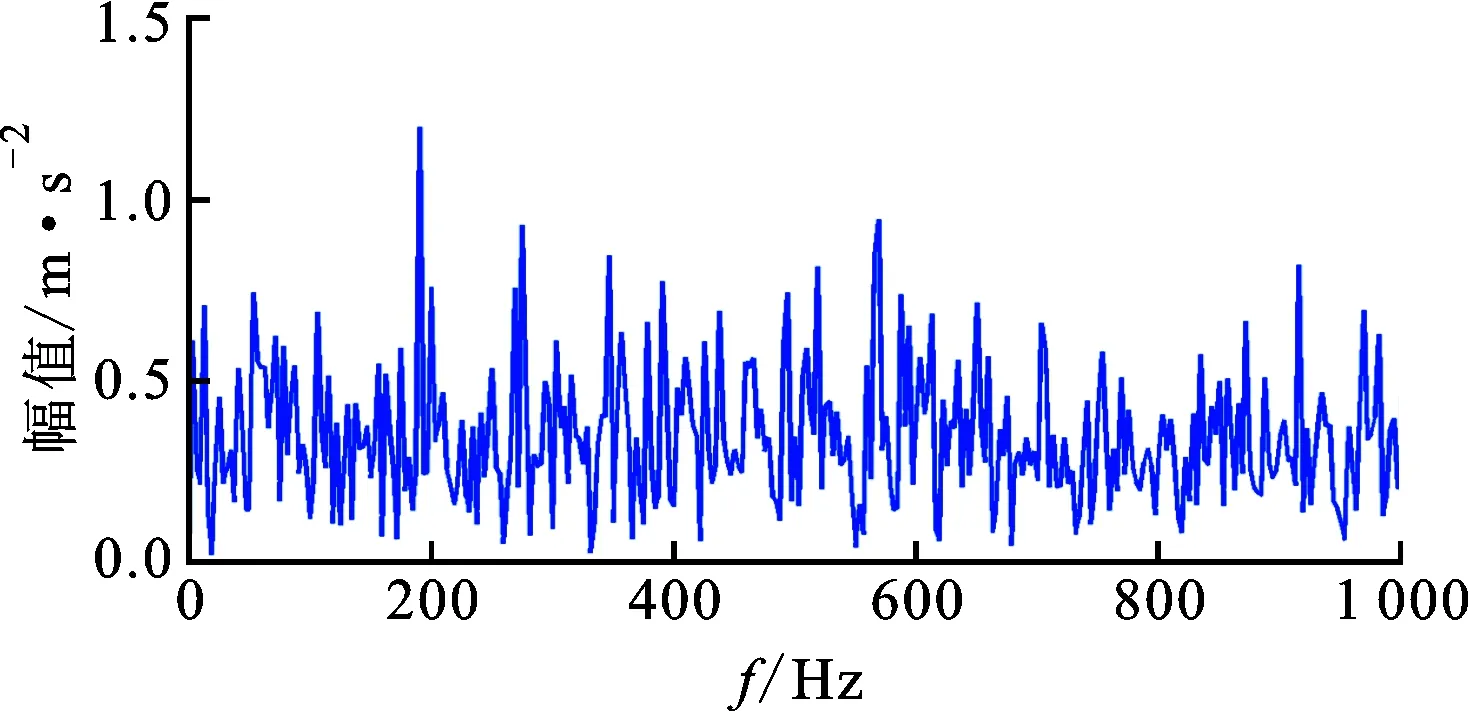
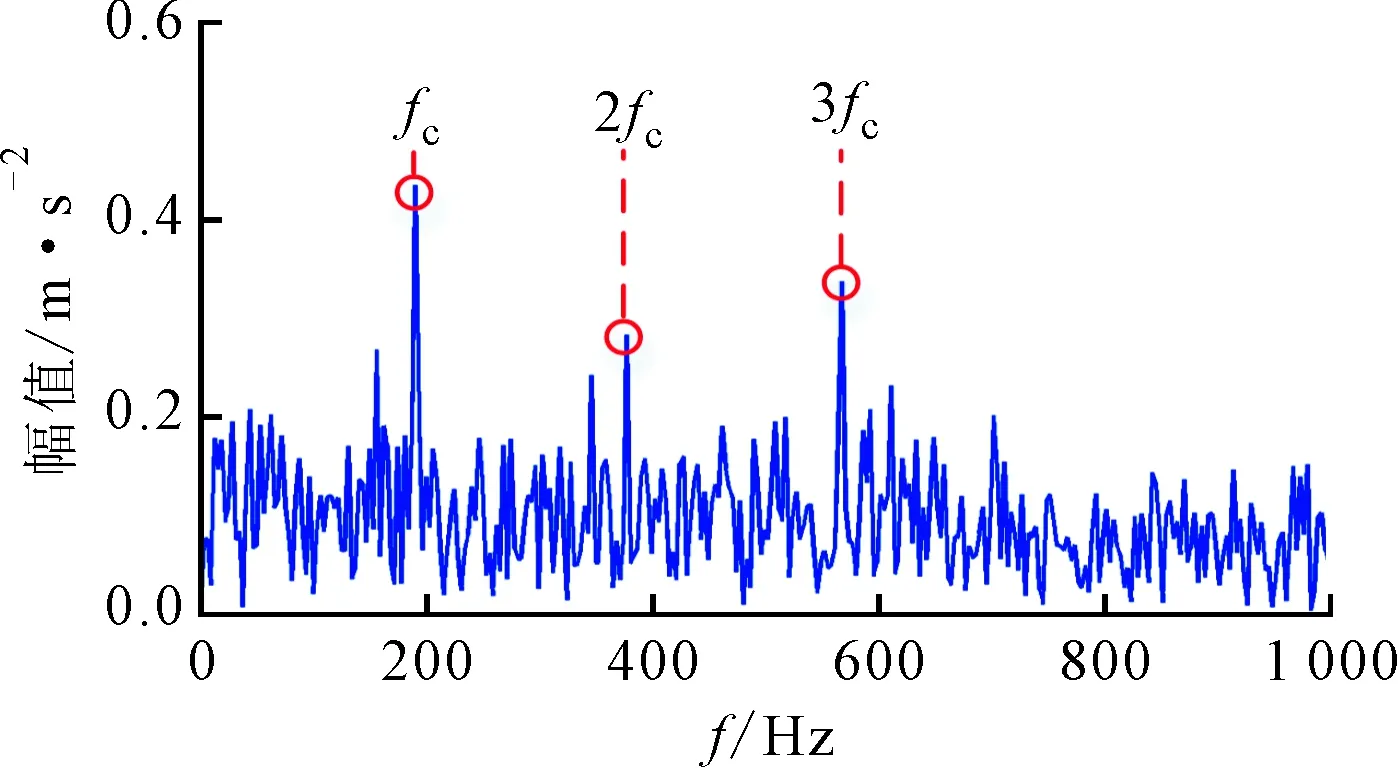
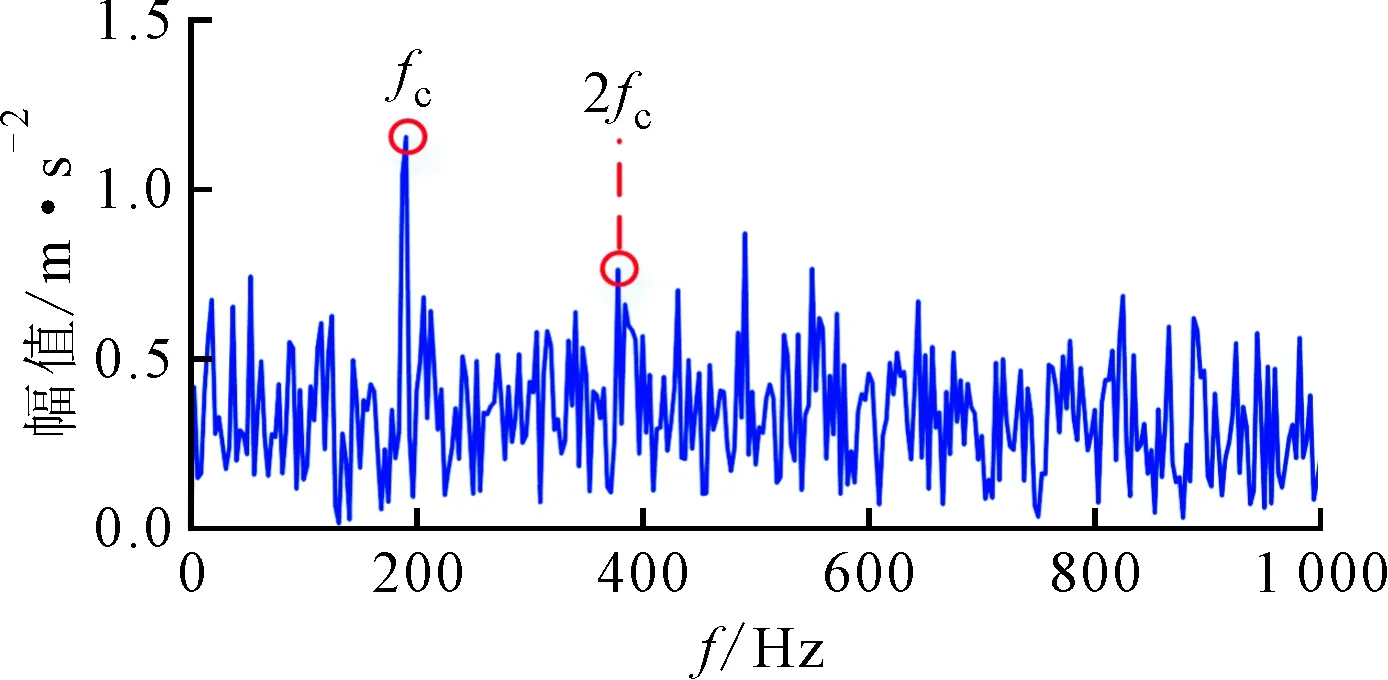
与在正交基上分析重构信号的方法不同,稀疏表示是将信号在一组冗余的基函数下展开,这组基函数叫做字典,记为矩阵A∈Rn×m(n (1) 式中:xγ是对应于αγ的表示系数;Γ是原子索引的参数集合。 由于字典是过完备的,也就是说原子集合是线性相关的,对y的分解是无穷多的。为了得到唯一解,稀疏模型假设信号是由少数几个原子表示的,即对解引入了稀疏正则化约束,这个问题可以表示为如下优化问题 (2) 式中:x∈Rm表示系数向量,x的l0范数表示其中的非零项的个数;ε是分解允许的误差。这个优化问题是非确定性多项式问题,可以采用如匹配追踪(MP)[13-14]、正交匹配追踪(OMP)[15-16]等贪婪算法求解;或者采用凸松弛方法,用l1范数替换l0范数,将问题转化为凸优化问题来求解,即基追踪去噪(BPDN)[17]方法。 在振动信号的稀疏表示中,字典A的选择是另一个重要问题。解析字典拥有快速算法,但只局限于表示某类振动信号。为了能根据信号原本的结构特征,构建出自适应字典,需要采用字典学习方法。字典学习的本质是在稀疏约束下,最小化信号表示误差,也就是如下优化问题 (3) K-SVD字典学习算法采用交替系数X和字典A的策略,在以下步骤中迭代。 (1)稀疏编码阶段。已知Y和A,用贪婪追踪算法如OMP估计表示系数矩阵X; 用贪婪算法求解稀疏表示系数时,低相关性的字典是获得最优表示的保障[18]。低相关性字典使原子能够表现出信号不同的结构特性,从而覆盖大部分信号集空间,利于用信号稀疏表示[19]。INK-SVD算法就是在K-SVD算法的基础上,加入了原子解相关的步骤。字典的相关性定义为不同归一化原子的内积绝对值中的最大值,公式如下 (4) 相关性μ的取值在0到1之间。当字典是正交时,μ取得最小值0;当字典中包含有两个原子共线时,μ取得最大值1。 要获得低相关性的字典,可以求解如下优化问题 (5) E←∅ (i,j)=arg max|AHA-I| A←A{ai,aj} E←E∪{ai,aj} end while 图1 两个原子解相关示意图 原子在标准正交基下的向量表示分别为 (6) (7) 可以推导出问题(5)的目标函数和约束分别为 (8) (9) 迭代地进行(1)(2)两步,就可以获得低相关性的字典,具体算法如下。 for ∀(ai,aj)∈Edo (ai,aj)解相关 end for end while 考虑到字典学习算法的计算量较大,原子的长度不能过长。在提取轴承冲击故障特征时,首先将测得的信号按步长Δn,分解成k列长度为n的信号段,组成样本矩阵Y。原子的长度需要满足包含一个完整故障冲击衰减波形的长度,但是过长的原子会带来过大的计算量,影响算法的使用性。因此,实际中通常原子的长度选择略大于一个完整故障冲击衰减的长度。 图2 基于INK-SVD的滚动轴承故障特征提取算法流程 在故障初期,滚动轴承的振动信号常常表现为周期性的冲击振荡和其他振动成分的叠加。因此,通过叠加周期冲击成分和高斯白噪声,构建轴承故障仿真信号,具体数学表达式如下 (10) 式中:yi(t)是单边衰减的冲击响应信号。为了更好模拟实际信号中的不确定性,冲击衰减信号的波形参数取为服从均匀分布的随机量:冲击幅值Ai服从区间[0.5,1]m/s2的均匀分布,阻尼比ζi服从区间[0.1,0.15]的均匀分布,无阻尼固有频率ωn服从区间[4 000π,6 000π]rad·s-1的均匀分布,冲击周期T=0.01 s,n(t)是独立同分布的零均值标准差σ=0.1的高斯随机信号。数据的采样频率是20 kHz,采样点数为1 024,仿真信号的波形如图3所示。 (a)周期冲击成分 (b)冲击和白噪声的合成信号图3 仿真信号的波形 图4 两种算法提取特征信号的信噪比对比 为了进一步验证方法在提取滚动轴承早期微弱故障特征时的有效性,进行了如下电机轴承故障模拟实验。实验台由一个2.2 kW的电机连接的转子系统以及拖动的负载组成。在电机的轴承外圈内置了一个微弱故障,如图5所示。轴承的型号是SKF6203,外圈故障特征频率计算公式如下 fc=0.5Zfa(1-(d/D)cosα) (11) 式中:Z是滚动体个数;d是滚动体的直径;D是节圆直接;α是滚动体的接触角。当输入轴转频1 Hz时,特征频率为4.932 Hz。 振动信号是由一个粘贴在电机轴承座上的加速度传感器采集,经由Sony数据采集系统,最终在电脑上处理并显示。采样频率为12.8 kHz。振动信号测试系统如图6所示。 (a)实验台 (b)外圈预制微弱故障图5 故障模拟实验 图6 故障模拟实验振动测试系统 对信号进行希尔伯特变换,再对得到复数信号的模值进行快速傅里叶变换,得到信号的包络解调谱。原始信号的时域波形以及包络解调谱如图7所示。从时域波形中,没有发现明显的冲击成分,在包络解调谱中,也没有突出的故障特征频率,因此不能直接诊断出轴承的故障。 (a)原始信号时域波形 (b)包络解调谱图7 原始信号波形及包络解调谱 (a)本文算法 (b)K-SVD算法 (c)MOD算法图8 几种算法提取特征的包络解调谱比较 采用本文提出方法处理该信号,参数选择如下:训练信号段的长度为128,样本为500,字典冗余度为2,最大相关性取为0.5。由提取的故障特征波形得到的包络解调谱如图8a所示。在该电机转速下,对应的fc是188.8 Hz,从中可以明显看到故障特征频率,及其2、3倍频成分,说明本文算法成功地诊断出滚动轴承的早期微弱故障。作为对比,用原始的K-SVD算法与MOD算法处理该段信号,得到的故障特征波形包络解调谱如图8b、8c所示,从中只能看出故障特征频率及其2倍频,不能看到明显的3倍频,表明其故障特征提取效果不如本文算法。 采用INK-SVD算法可以得到低相关性的字典,保证了稀疏表示的求解精度,提高了原子与故障特征信号的匹配程度。通过合理设定相关性、训练样本长度等参数,基于非相关字典学习可以有效提取滚动轴承故障稀疏特征。仿真分析及实验分析表明,与传统字典学习方法相比,本文算法可以更加精确地恢复稀疏系数,在重构信号的包络解调谱中更有利于故障特征的辨识。2 滚动轴承故障诊断
2.1 字典学习问题与K-SVD算法

2.2 INK-SVD算法
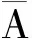
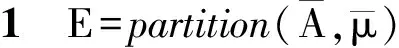

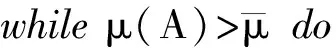
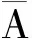

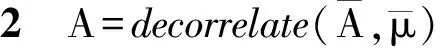

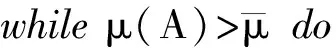
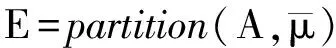
2.3 故障特征提取
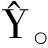
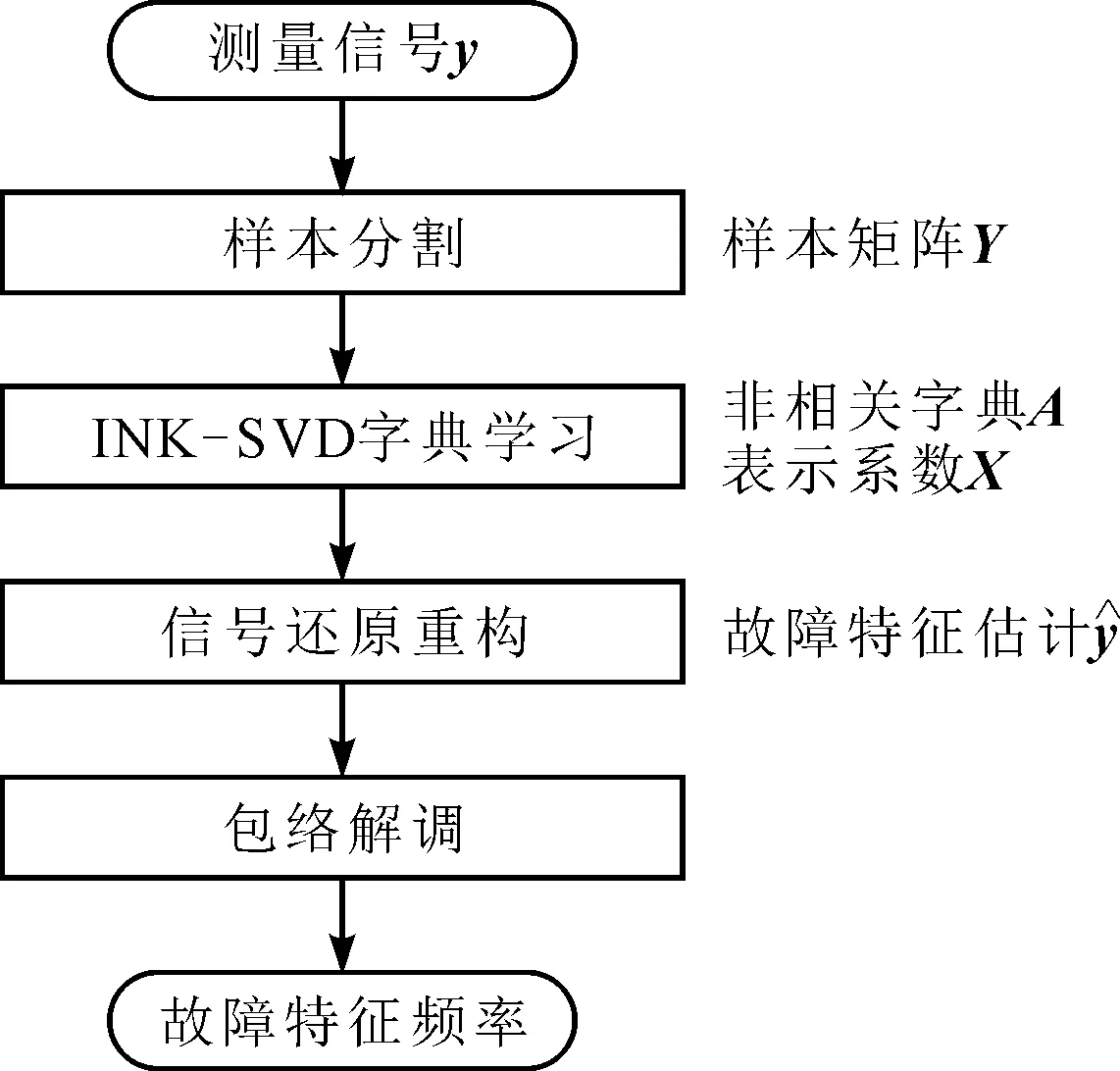
3 仿真分析
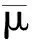



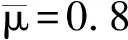
4 故障模拟实验



5 结 论

