面向多品种小批量生产的贝叶斯动态质量控制方法
陈鑫,陈富民
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
随着经济的发展,用户需求日益多样化,多品种小批量生产已逐渐成为了制造业的主导模式[1]。然而,由于该种模式数据量少、产品参数多变等特点,传统的统计过程控制(SPC)方法的应用收效甚微。因此,如何有效解决多品种小批量生产的质量控制问题成为当前研究的热点[2]。
近年来,国内外学者在此方面进行了大量研究。部分学者将扩充数据量作为研究重点,如余忠华等提出了基于相似元的工序相似性分析方法,并应用于SPC技术中[3];吴小勇引入了直觉模糊集理论来解决成组工序构建中的相似性评判问题,将相似工序分类成组进行分析[4];WIEDERHOLD等通过识别相似生产过程并将它们的数据进行聚类从而增加样本量[5]。还有一些学者致力于质量控制方法研究,如牛占文等针对多品种小批量生产模式下SPC应用效果不佳的问题,提出结合应用通用控制图、累计和控制图、指数加权移动平均值控制图的解决方法[6];GU等分析了各种质量控制方法的不足之处,提出了一种新型的t控制图来监测产品质量[7]。
现有大部分研究只关注于历史生产数据或当前生产数据之一,产生了很大的信息浪费。贝叶斯理论从历史数据等先验知识中提取所需信息,结合现有数据就能有效解决多品种小批量生产模式下数据量少的问题。目前,已有一些学者将贝叶斯理论应用于中小批量生产的质量控制中,取得了一定的成果[8-10]。然而,此类研究大多只利用单一产品的质量数据,不太适用于多品种小批量生产模式。
针对新模式下的工序质量控制问题,本文基于贝叶斯理论,提出了一种动态质量控制方法。首先根据成组技术和统计变换从历史生产批次中扩充数据量作为先验信息;然后融合指数加权思想,应用共轭贝叶斯方法建模,计算相应的工序能力指数,随着生产过程的进行实时计算控制限,实现动态质量控制;最后通过仿真比较本文方法与现有常用方法的优劣,结果表明,本文方法在生产的各个阶段都有更好的控制效果和异常检出力,可为多品种小批量生产模式提供一种有效的质量控制方法。
1 选取先验信息
在开始质量控制之前,应该分析企业生产状况,以确定需要进行质量控制的关键质量特性等信息。针对关键质量特性,根据成组技术收集过去一定时间段内满足要求的历史质量特征数据,通过统计变换方法,使各批次历史数据满足“独立同分布”的要求,然后以变换后数据作为贝叶斯建模的先验信息。
1.1 成组技术
按照一定的相似性准则将产品分类成组是成组技术的核心[11]。将成组技术应用到多品种小批量质量控制,企业应该侧重于对产品质量影响较大的关键工序来制定相似性分类标准。
目前,相似工序的分类方法主要有4种:目测分类、生产流程分析[12]、编码分类[13]、聚类分析[14]。企业应根据实际情况选择适合的方法,然后从人、设备、物料、方法、环境、测量6个方面[15]制定分类准则,将相似工序分类成组。对关键质量特性进行质量控制前,收集相关关键工序同组内的历史批次质量数据,作为备选先验信息。
1.2 数据变换
由于各批次历史数据来自不同品种的产品,不满足“独立同分布”要求中关于“服从同一个分布”的条件,所以需要对这些数据进行变换,使各批次数据具有相同的分布。
进行数据变换的准则有两点:①消除不同过程均值所带来的影响;②消除不同的公差带来的影响。基于变换准则,可以确定数据变换方式为
(1)
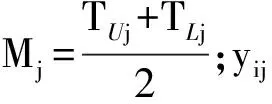
2 贝叶斯建模
2.1 制作控制图
随着生产的进行,产生了n个质量特征数据,经过数据变换后为{y1,y2,…,yn}=Y,假设Y的总体分布为正态分布N(μ,σ2),则控制图控制限为
(2)
由式(2)可知,对质量控制的效果主要取决于对超参数μ、σ估计的准确程度。利用贝叶斯方法进行动态建模能够充分利用先验信息,随着生产过程的进行,逐渐提高对μ、σ估计的准确度,从而达到更好的质量控制效果。
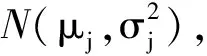
(3)
式中:nj为第j批历史数据样本容量。
由于多品种小批量生产条件多变,加工时间更接近当前生产的历史批次应当更能反映当前的生产状况,所以根据时间序列对各批次历史数据进行指数加权。
由于多品种小批量生产的特性,各企业所采取的检验方式(全检或抽样检验)和抽样方法不同,各批次数据量也可能不相同,故求取组间均值和组间方差时使用变样本容量的计算公式。
上述两方面相结合,可得历史数据的组间均值与组间方差为
(4)
式中:k为加权系数,一般取为(N+14)/14,N为平均各批次的生产天数;m为先验信息的历史数据总批次。
(2)求μ、σ2估计值。由于μ、σ2为正态分布的超参数,根据共轭贝叶斯理论[16],可设σ2的先验分布为逆Gamma分布,记为IGa(α,β),μ的先验分布为正态分布,考虑到μ和σ2间有相互影响,故其共轭先验分布有乘积形式π(μ|σ2)π(σ2),其中
μ|σ2~N(a,b2);σ2~IGa(α,β)
①估算σ2。对于σ2~IGa(α,β),根据逆Gamma分布的性质,其期望和方差分别为
(5)
(6)
联立(5)(6)两式,可得
在得到当前批数据Y后,根据共轭分布性质可知,后验分布形式与先验分布相同,故可设
(7)
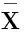
因此,可得σ2的贝叶斯估计为
(8)
②估算μ。对于μ|σ2~N(a,b2),由正态分布的性质,可得期望为
在得到当前批数据Y后,根据共轭分布性质可知
μ|σ2,Y~N(a′,b′2)
由共轭贝叶斯,可得(μ,σ2)的联合先验密度函数为
π(μ,σ2)∝
因此,μ的边缘后验密度

这是自由度为(2α+n)的t分布,其中
则可得μ的贝叶斯估计为
μB=E(μ|Y;μ1,μ2,…,μm)=a′=
(9)
(3)计算控制限。由于多品种小批量生产的数据量小,选用单值-移动极差(X-MR)控制图,结合实时生产数据,使用式(8)(9),计算σ、μ的贝叶斯估计值,求单值图的控制限
移动极差的控制限为
(10)
(11)
2.2 工序能力分析
若当前生产批次处于受控状态,应该计算工序能力指数,来判断工序能力是否满足要求。常用(双边公差)的工序能力指数计算公式如下
(12)
(13)
式中:Cp为分布中心与公差中心重合时的无偏移工序能力指数;Cpk为有偏移工序能力指数;μx、σx分别为原始数据的均值和标准差。根据数据变换式(1),可知
(14)
将μ=μB,σ=σB代入式(14),然后结合式(13)可得工序能力指数计算式如下
然后,根据工序能力评价标准[17]进行评判。
3 仿 真
以某柴油机加工车间的镗喷油器孔工序为例,利用仿真生成数据,比较本文方法与现有常用方法的优劣。

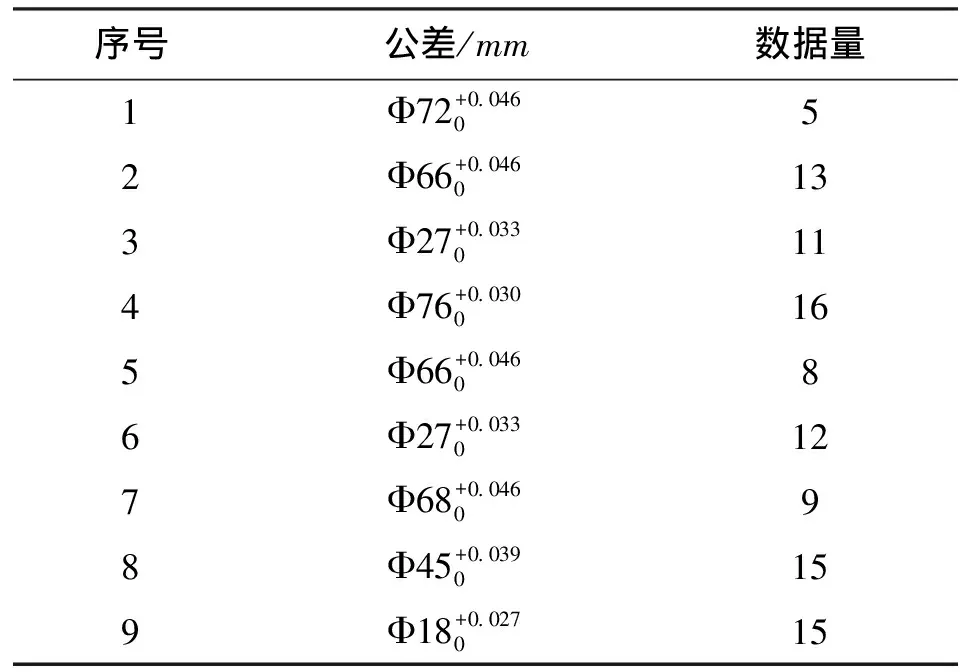
表1 历史质量特征数据
3.1 分布参数估计误差分析
应用休哈特控制图进行质量控制的效果主要取决于对分布参数估计的准确程度,故通过仿真比较本文方法与两种现有常用方法对参数μ、σ的估计情况,说明本文方法的可行性。
针对上述柴油机加工车间的质量控制问题,两种现有常用方法的处理过程如下。
方法1:通过成组技术、数据变换和假设检验方法,利用多品种的历史批次扩充数据量,每批历史数据取5个,计算各批次历史数据均值及标准差的平均值作为参数μ、σ的估计值,然后计算控制限,使用此固定控制限对工序质量进行控制。
方法2:利用当前生产数据的均值与平均移动极差,计算μ、σ的估计值,随着生产的进行实时计算控制限。
具体仿真过程如下:
(2)根据表1,从母体取9批数据作为历史数据;
(3)根据历史数据,按照方法1计算均值和标准差的估计值μm1、σm1,求估计误差的绝对值(如均值估计误差eμ,m1=|μm1-0|);
(4)根据当前批数据,以方法2计算均值和标准差估计值μm2、σm2,然后求估计误差的绝对值;
(5)根据历史数据和当前批数据,以本文方法计算μB、σB,求估计误差的绝对值;
(6)从步骤(1)至(5)记为完成一次仿真,一共进行1 000次仿真,求当前批样本容量为n时的平均参数估计误差;
(7)令当前批样本容量n=n+1,返回步骤(1)。
随着当前批样本容量的增加,3种方法对参数μ、σ的估计值平均误差的变化见图1。从图1可以看出:方法1在生产初期误差较小,在当前批样本容量较大时适用性较差;方法2只适用于当前批样本容量较大的情况;本文方法在整个生产阶段都有更好表现,并且随着当前批样本容量的增加,估计误差逐渐减小,较两种现有常用方法有明显优势。

(a)均值误差

(b)标准差误差图1 分布参数估计平均误差
由于方法1的准确性依赖于历史数据的可靠程度,当历史批次数据量减少或波动加剧时,方法1的控制效果显著下降。由于多品种小批量生产的复杂特性可以预期,在实际生产中,本文方法的优越性会更加明显。
3.2 平均运行链长
平均运行链长(ARL)是评价控制图性能的重要指标[18]。生产过程处于稳态时的平均运行链长记为LARL,0,生产过程发生异常波动时的平均运行链长记为LARL,1。LARL,0越大表示控制图误报率越低,LARL,1越小表示控制图的漏报率越低,即异常检出力越强。
据研究表明[19],当累积和(CUSUM)控制图的参数k=0.5、h=4.77时,其受控平均运行链长LARL,0与常用的休哈特控制图相当。因此,在该参数情况下,比较累积和控制图方法与其他休哈特控制图相关方法的LARL,1,以比较各方法的异常检出力。
方法3(累积和控制图):通过成组技术、数据变换和假设检验方法,利用多品种的历史批次扩充数据量,每批历史数据取5个,计算各批次历史数据标准差的平均值作为分布参数σ的估计值σC,作累积和控制图,其中参数K=0.5σC,H=4.77σC。
利用仿真方法估计从不同位置开始发生波动时本文方法及其他3种现有常用方法的LARL,1。仿真过程如下:
(3)分别应用3种常用方法和本文方法进行控制,计算从开始发生波动到控制图报警之间的运行链长;
(4)从步骤(1)至(3)记为完成一次仿真,一共进行1 000次仿真;
(5)计算各方法的LARL,1;
(6)令p=p+1,返回步骤(1)。
表2列出了随着发生波动位置的变化,各种方法LARL,1的变化。
从表2可以看出,当受控生产数据较少时,方法1的LARL,1与本文方法接近,均小于方法2与方法3。随着受控生产数据的增加,本文方法的优势渐渐呈现,LARL,1明显小于其他3种方法。因此,当标准差发生波动时,本文方法有更强的异常检出力。
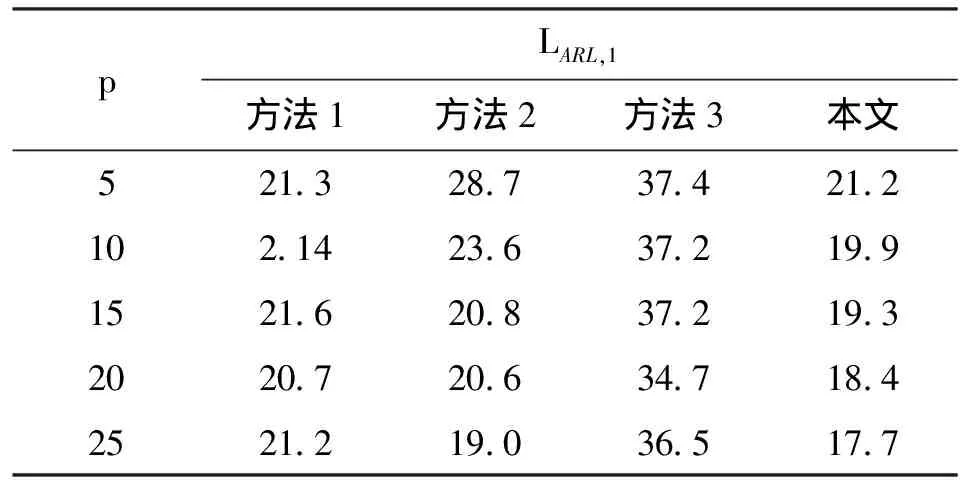
表2 几种方法平均运行链长LARL,1的比较
4 结 论
结合成组技术、指数加权及贝叶斯理论的优点,提出了一种动态质量控制方法。首先使用成组技术和数据变换方法扩充数据量作为先验信息;然后结合指数加权思想及贝叶斯理论建模,并计算工序能力指数;最后通过仿真验证了该方法的有效性。与现有常用方法相比,本文方法在适用范围、控制效果、异常检出力等方面均有提高,一定程度上解决了多品种小批量生产模式下的质量控制问题。在后期工作中,可以进一步研究抽样方法和分组准则等因素对质量控制的具体影响,进一步提高多品种小批量生产的质量控制效果。

