投资者情绪会引发黑天鹅吗？

杨青 周文龙

（复旦大学经济学院，上海 200433）

一、引言

金融市场中的极端价格波动具备发生概率小、难以预期及破坏性大的特征，受到学术界、业界及监管层极大的关注。全球金融市场范围内，1929年10月24日和29日美国股市遭遇“黑色星期四”和“黑色星期二”的大崩盘，1987年10月19日道·琼斯指数狂跌22.6%，史称“黑色星期一”，1997年亚洲金融危机，1998年美国长期资本管理公司(LTCM)破产倒闭事件，2008年全球金融危机，这些极端金融事件都对相关国家和地区的金融体系造成了巨大的冲击，金融稳定和安全受到极大挑战。

近年来，中国资本市场持续深化改革，市场机制和制度日益趋于完善，但“黑天鹅”事件依然时常对金融稳定和安全构成威胁。2013年6月20日的“钱荒”事件，SHIBOR隔夜拆借利率飙升至13.44%的纪录高点；2013年8月16日的“光大乌龙指”事件，大盘一分钟内涨幅超过5%；2015年股灾期间，多次上演千股跌停的异常景象；2016年1月4日至7 日，4次触发熔断机制；2018年中美贸易战持续推进，股市再次频繁剧烈地波动。在可预期的未来，国际国内经济环境异常复杂，金融市场面临极端风险的冲击和考验，如何有效防范和化解系统性金融风险，维护金融安全和稳定显得尤为重要。针对中国金融市场极端风险事件以及对市场潜在系统性风险前瞻性预防的考虑，2017年7月，《人民日报》密集发表评论员文章讨论如何有效防范中国金融市场风险问题，可见中国政府对金融市场稳定发展这一国家经济金融战略的重视。

与之同时，中国经济总体运行平稳，经济基本面从未发生根本性变化，根据投资者情绪相关理论如DSSW模型(De Long et al.，1990)，BSV模型(Barberis et al.，1998)，DHS模型(Daniel et al.，1998)，噪声交易者在中国资本市场的剧烈震荡中扮演了重要角色，投资者情绪和市场波动有很强的关联性。所谓投资者情绪，是指投资者关于市场的态度和看法，一般表现为悲观或者乐观的状态。金融市场本质上是众多投资者构成的市场，投资者依据金融市场上的各类信息做出决策，进而影响资产的收益及波动性。投资者悲观或乐观的心理会影响其对各类信息的解读从而影响其投资决策。当众多投资者趋同性地表现出极度悲观或极度乐观的时候，即投资者情绪极度高涨或极度低落的时候，市场极易发生极端的价格波动。

目前有关投资者情绪的研究往往聚焦于投资者情绪和资产收益及其波动的关系，较少从投资者情绪和极端市场风险之间关系的角度进行研究。基于此，本文从实证方面研究投资者情绪和极端市场风险之间的关联性。研究发现，投资者情绪和极端市场风险之间存在双向的溢出关系；相对于小盘股，大盘股的极端市场风险更能影响投资者情绪，而投资者情绪对小盘股的极端市场风险影响最大；相对于高市净率股票，投资者情绪对低市净率股票的极端市场风险影响较小，而高市净率股票的极端市场风险对整体市场投资者情绪的影响力较小。

本文的边际贡献在于进一步拓展了对极端市场风险生成机理的研究视角。通过将投资者情绪和极端市场风险相关联，本文得以更深入探讨投资者心理层面的变化对极端市场风险的影响及极端市场风险对投资者心理层面的反馈效应，不仅有助于更好认识极端市场风险的生成机理，而且对防范市场风险、维护金融安全和稳定有一定的启示。

本文的结构如下：第二部分回顾投资者情绪和极端市场风险这两个研究领域的相关文献；第三部分说明本文的研究方法和数据来源；第四部分实证检验投资者情绪与极端市场风险的关联性；第五部分为研究结论。

二、文献综述

本文的研究主题是投资者情绪与极端市场风险之间的关联性。与本文密切相关的文献来自投资者情绪与极端市场风险这两个研究领域。

(一)投资者情绪相关文献回顾

传统金融理论认为，资产价格的波动主要源于基本面的波动。行为金融理论不仅承认基本面波动对资产价格的影响，同时重视投资者情绪对资产价格的扰动。投资者情绪能对资产价格波动产生作用的原因在于套利的有限性(Shleifer and Vishny，1997)。De Long et al.(1990)构建了一个迭代的“DSSW模型”，假定市场中同时存在理性套利者和噪音交易者，其交易行为共同影响资产均衡价格。在基本面未发生波动的情况下，噪声交易者的存在也会导致资产价格大幅偏离资产内在价值。基于心理学中的两大证据，即投资者的保守性和代表性偏差，Barberis et al.(1998)提出描述投资者信念形成过程的“BSV模型”，并用以解释股票价格对新信息的过度反应(overreaction)和反应不足(underreaction)现象。对于过度反应和反应不足现象的解释，DHS模型(Daniel et al.，1998)引入了两大心理学中的偏差，即过度自信(overconfidence)和自我归因偏差(biased self-attribution)。Lee et al.(1991)研究了个人投资者情绪对封闭式基金折价波动的驱动。实证方面，投资者情绪对资产定价的系统性影响得到了进一步证实(Brown and Cliff，2005；Baker and Wurgler，2006；Yu and Yuan，2011；Stambaugh et al.，2012)。例如，Baker and Wurgler(2006)研究了投资者情绪对股票收益的横截面效应，发现投资者情绪对估值高度主观和不易进行套利交易的股票能够产生更大的效应。Stambaugh et al.(2012)研究了投资者情绪对11个资产定价异象的解释作用。

国内学者以DSSW模型为基础，结合中国金融市场及参与者的特征，对这一模型进行了相应的拓展和改进，认为投资者情绪能显著影响资产的均衡价格(王美今和孙建军，2004；张宗新和王海亮，2013)。其中，王美今和孙建军(2004)在 DSSW 模型基础上，将噪声交易者细分为情绪型噪声交易者和其他交易者，通过理论模型和实证检验得出以上结论。而张宗新和王海亮(2013)综合 DSSW 模型与贝叶斯学习过程，并在模型中引入主观信念调整，探讨其在处理信息和影响情绪过程中的作用。胡昌生和池阳春(2013)研究了市场不同估值阶段投资者情绪与市场波动性之间关联的差异性。文凤华等(2014)探讨了投资者情绪特征对股票价格行为的影响，发现正面情绪和向上的情绪波动对股票收益率存在显著的正向影响。段江娇等(2017)从海量的互联网文本信息中挖掘投资者情绪成分，研究发现帖子情绪对股票收益率、波动性及交易量存在显著影响。部慧等(2018)发现基于股评的投资者情绪无法预测股票收益率、波动性及交易量，但对收益率和交易量存在当期影响。

(二)极端市场风险相关文献回顾

一般而言，金融资产收益具有尖峰厚尾的特征，而广泛应用的正态分布并不能描述实际金融资产收益的这种特征。极值理论仅考虑尾部分布，不用对整个分布进行假设，能够很好处理风险度量中的厚尾问题。Pickands(1975)对经典的极限定理进行了证明，指出可以运用广义帕累托分布(Generalized Pareto Distribution，GPD)对超额数分布函数进行拟合，为以后的风险建模做出了突出贡献。Longin(1996)以美国股票市场1885年至1990年的日度数据为样本，运用极值理论对极端市场波动进行建模，开创了将极值理论运用于风险管理的先例。之后，Longin(2000)又全面系统地介绍了运用极值理论计算在险价值(Value at Risk，VaR)的方法。基于这种方法，Ho et al.(2000)分析了6个陷于金融危机的亚洲国家和地区的股票市场。尽管VaR是度量风险的有效手段，但其本身主要存在两方面的缺陷：一是没有测度高于VaR值的极端损失发生的概率，即没有充分考虑尾部风险；二是VaR不满足次可加性，违背了分散化投资降低投资组合风险的原则，因而不是一致的风险度量工具。针对VaR这两方面的缺陷，Artzner et al.(1997，1999)提出了期望损失(Expected Shortfall，ES)模型，该模型从VaR衍生而来，弥补了VaR不满足次可加性及没有考虑尾部风险等缺陷，其测度了高于VaR值损失的条件期望值。

借鉴国外有关极值理论的研究成果，国内学者将其应用于金融市场风险度量的实证分析中。陈学华和杨辉耀(2004)研究发现基于广义极值分布的VaR模型很适合刻画高频时间序列的尖峰后尾特征及杠杆效应，ES模型则很好地弥补了VaR模型的缺陷。陈守东等(2007)以上证指数日对数收益率数据为样本，采用极值理论中的广义Pareto分布进行建模，得到度量风险的VaR和ES值，研究发现在置信水平较高的条件下，运用极值方法测度风险效果更好。魏宇(2008)认为条件极值分布在度量极端市场风险方面存在优势。杨青等(2010)研究发现极值理论是分析金融市场极端风险的有效手段，且A股市场极端风险高于港股和美股。陈新春等(2017)研究了基金信息网络对极端风险的影响机制，发现机构投资者之间的信息联系和传递容易引起黑天鹅事件。

以上研究成果对于理解投资者情绪对市场波动的影响及测度极端市场风险都具有积极作用，但缺乏对投资者情绪和极端市场风险之间关联性的研究。基于此，本文将投资者情绪与极端市场风险相联系，研究投资者情绪在极端市场风险生成过程中的作用及极端市场风险对投资者情绪的反馈效应。

三、研究方法与数据来源

(一)研究思路和方法

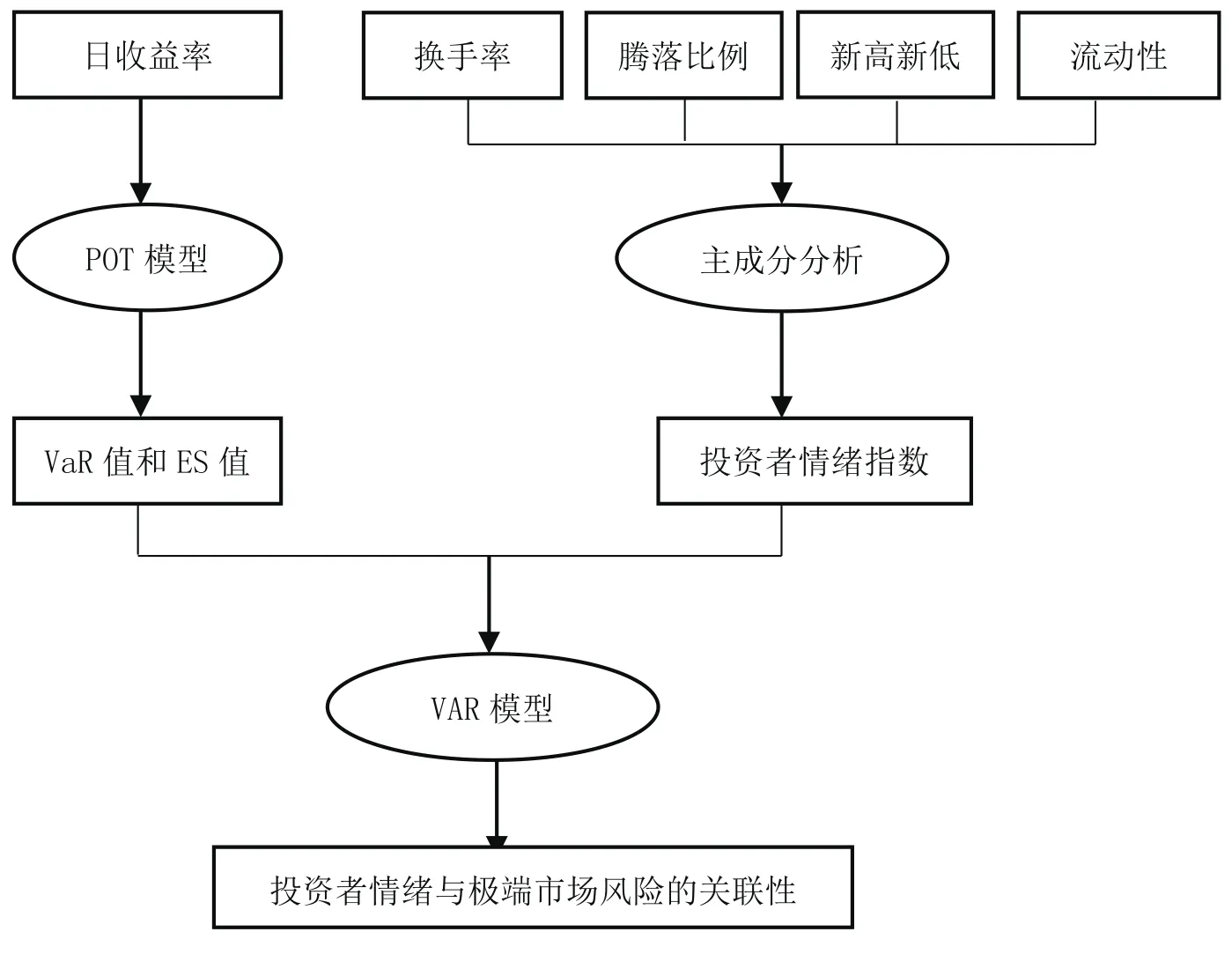
图1 研究思路和方法

基于以上研究目标，本文确定的研究思路如图1所示：首先，参照Baker and Wurgler(2006)的做法，选取中国股市流动性、换手率、腾落比例及新高新低指标作为投资者情绪代理指标，采用主成分分析法提取共同的投资者情绪成分，构建投资者情绪指数。然后，运用超阈值(Peak Over Threshhold，POT)模型来度量极端市场风险，分别计算测度极端市场风险的VaR值和ES值。最后，本文使用向量自回归(Vector Autoregressive，VAR)模型研究投资者情绪和极端市场风险之间的关系。因此，本文使用的研究方法主要涉及主成分分析法、超阈值模型及向量自回归模型。

1.主成分分析法。

主成分分析法是通过一组变量的少数几个线性组合来解释该组变量的方差和协方差结构，从而实现降维处理的目的的一种多元统计方法。本文选取中国股市流动性、换手率、腾落比例及新高新低指标作为投资者情绪代理指标，利用主成分分析法从中提取共同的投资者情绪成分，剔除其他的非情绪成分，构建投资者情绪指数st。

2.超阈值模型。

POT模型对观测值中所有超过某一较大阈值的数据建模。假设x为资产收益率，F(x)为资产收益率分布函数，u为给定的阈值，x-u表示超额数值，则其分布函数定义如下：

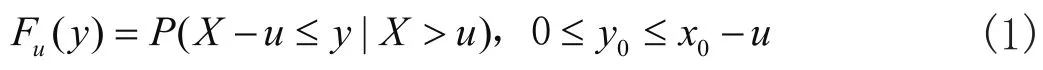
易得，

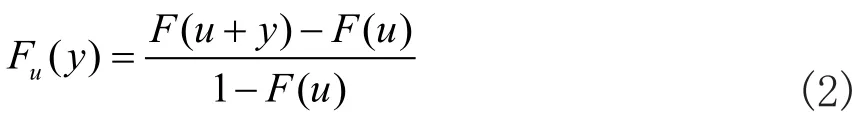
当阈值u充分大时，超额数值的分布函数Fu可以用GPD分布近似。对于x＞u，由式(2)可知，F(x)的尾部估计表达式可以构造如下：

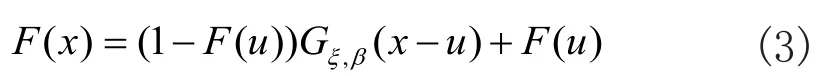
总而言之，对F(x)的估计可按如下步骤进行：首先，选定适合的阈值u；其次，运用极大似然估计法估计GPD分布的形状参数ξ及尺度参数β；然后，对F(u)进行估计；最后，对尾部分位数进行估计。将所有估计量代入式(3)，得到F(x)的尾部估计表达式：

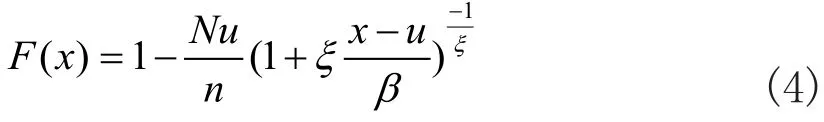
进一步，可以定义极端风险VaRc在不同概率水平c下的在险价值，得到VaRc的表达式：

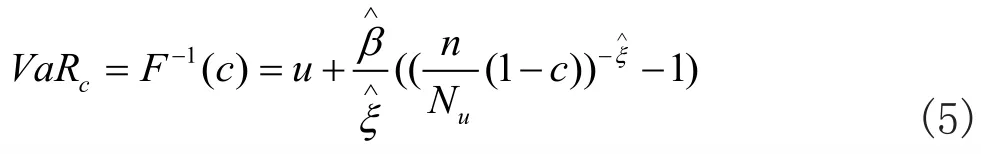
ES度量了损失超过VaR水平的条件期望值，其表达式为：

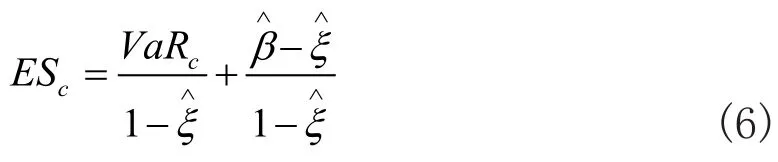
为了从动态角度对VaR和ES值进行估计，本文将广义自回归条件异方差(Generalized AutoRegressive Conditional Heteroskedasticity，GARCH)模型与POT模型结合，基本步骤如下：首先，运用GARCH模型拟合日收益率数据，采用极大似然估计法进行估计，得到拟合后的残差；然后，利用POT模型分析拟合后的残差，求出残差的VaR和ES值；最后，依据残差与日收益率的关系求得日收益率的VaR和ES值。

3.向量自回归模型。

为了实证研究投资者情绪和极端市场风险之间的关联性，本文构建如下的VAR模型：

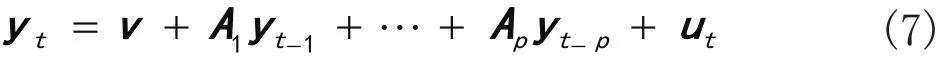
(二)数据来源

本文所使用的中国股市换手率、腾落比例及新高新低指标数据来自国泰安(CSMAR)数据库，沪市流动性、深市流动性及日收益率数据来源于万得(WIND)金融数据库。本文中用到的指标名及含义或计算公式如表1所示。本文的研究样本期间为1995年12月20日至2017年12月29日，共5342组数据。

表1 指标名及含义或计算公式说明

四、实证结果与分析

(一)投资者情绪指数的构建

本文选取了5个投资者情绪代理指标，其描述性统计及相关性如表2所示。表2列出了沪市流动性(Hiliq)、深市流动性(Siliq)、市场换手率(Turn)、腾落比例(ADR)及新高新低(NetNum)5个投资者情绪代理指标的均值、标准差、最小值、最大值以及这五个指标间的相关系数。从中可以看出，它们之间的相关性均在1%的水平下显著。

单个投资者情绪代理指标中都隐含了情绪成分和与情绪不相关的异质成分。为了构造投资者情绪指数，对这五个指标进行主成分分析，剔除代理指标中的异质成分，提取共同的投资者情绪成分。前两个主成分的累计方差解释率达到了66.97%，且仅有前两个主成分的特征值大于1。因此，本文选取前两个主成分按照各自方差解释率进行加权来构造投资者情绪指数。经构造得到的投资者情绪指数具有良好的性质，与5个投资者情绪代理指标均在1%的水平下显著相关。

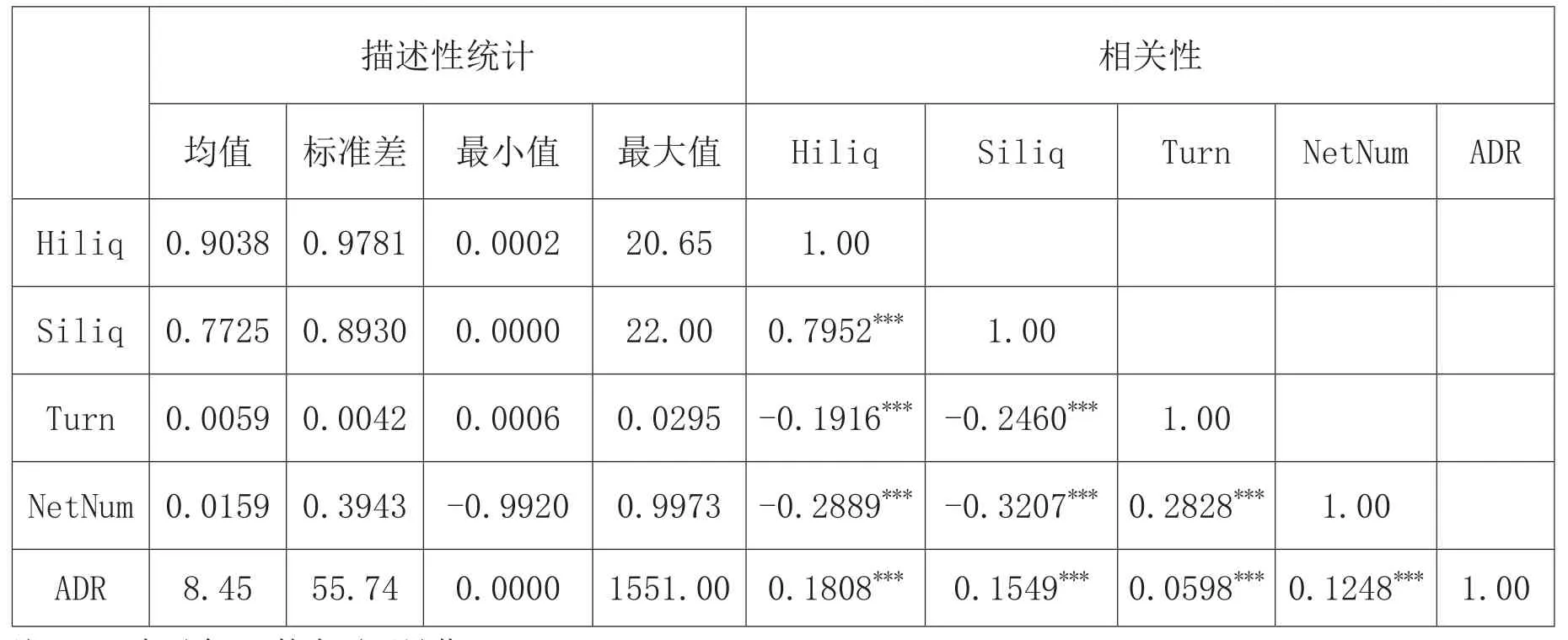
表2 投资者情绪代理指标描述性统计及相关性

(二)极端市场风险的测度

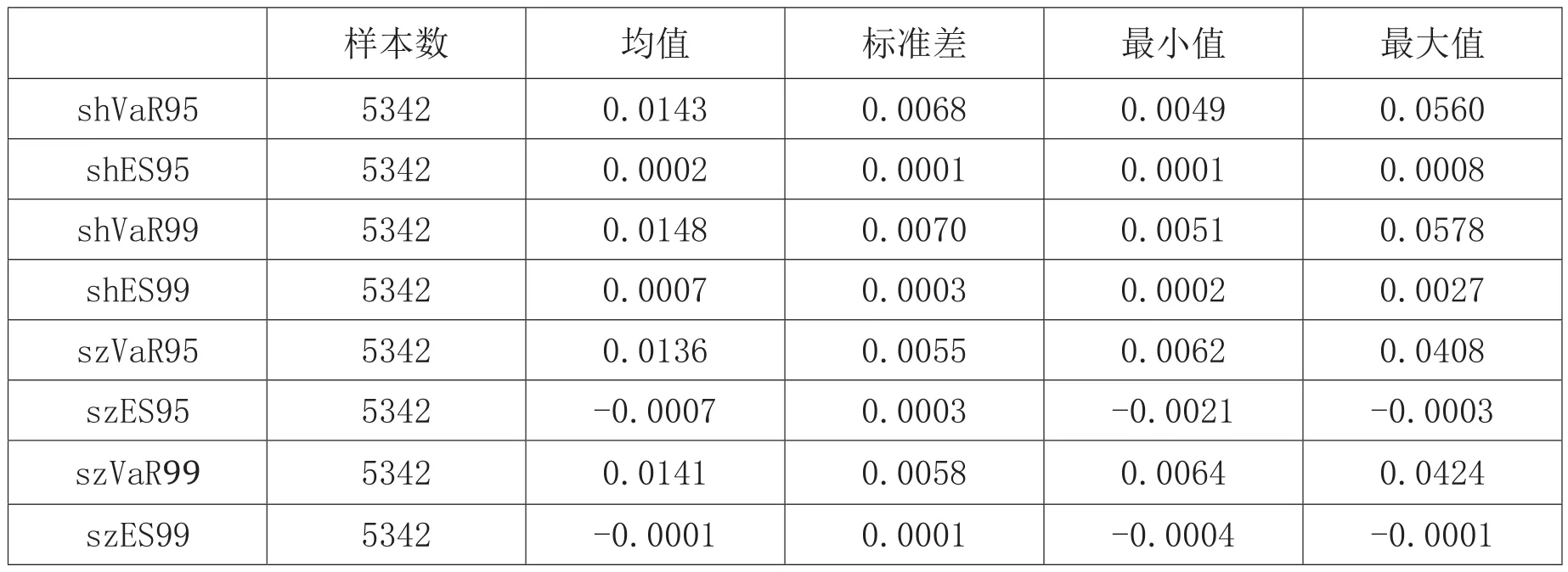
表3 极端市场风险测度值描述性统计

基于稳健性的考虑，本文分别计算了上证综指和深证成指在95%和99%分位数下的VaR和ES值。在计算极端下跌市场风险的VaR和ES值时，本文首先对日收益率数据取负号，运用极值方法计算得到的分位数再取负号，最终得到测度极端下跌市场风险的VaR和ES值。本文总共计算了8个测度极端市场风险的序列，其描述性统计见表3。

(三)投资者情绪与极端市场风险

为了避免伪回归问题，本文在模型回归之前对时间序列数据的平稳性进行检验。本文运用ADF法检验极端市场风险的测度值和投资者情绪指数是否存在单位根，检验结果如表4所示。

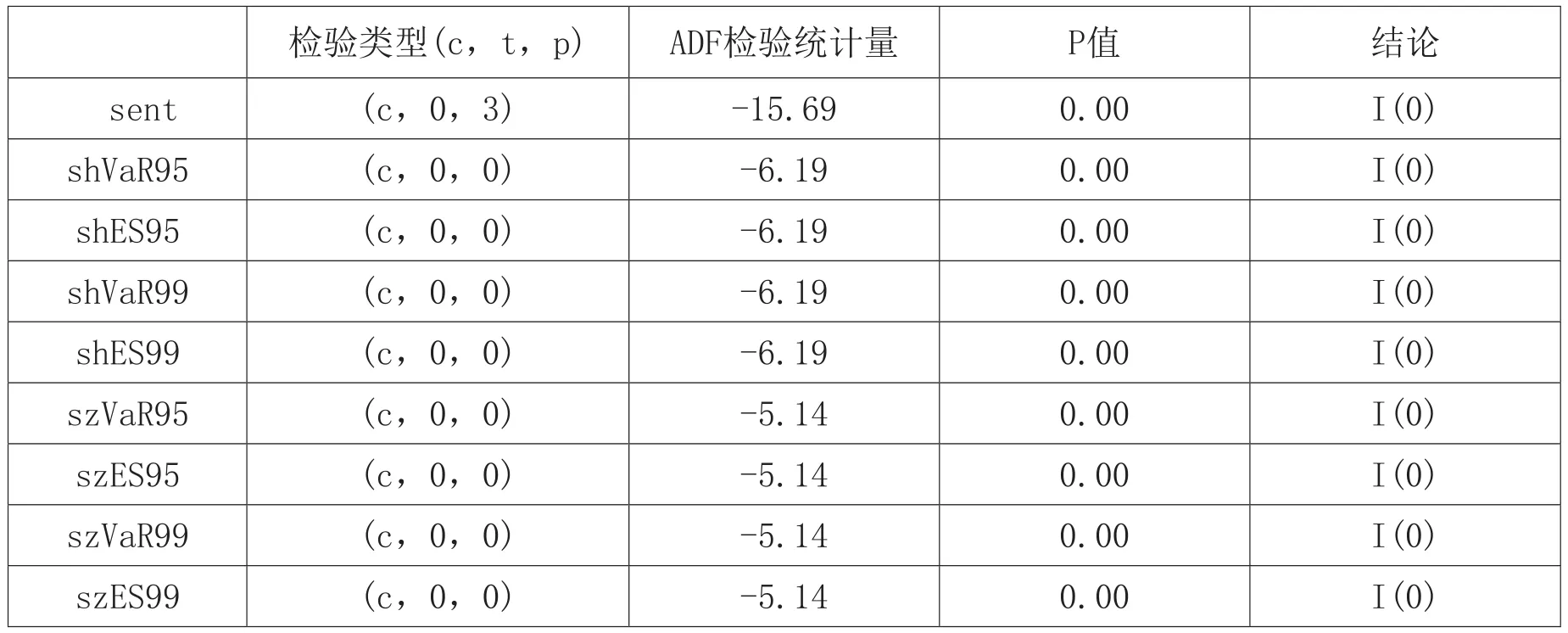
表4 投资者情绪指数与极端市场风险测度值单位根检验结果

由表4可知，投资者情绪指数序列和8个极端市场风险测度值序列均是平稳序列，符合零阶单整I(0)。

表5报告了投资者情绪指数和上证综指极端下跌市场风险VaR值之间的VAR模型的估计结果。在VAR模型中，本文根据AIC和BIC信息准则得到VAR模型的最优滞后阶数均为2阶。

对于投资者情绪指数和上证综指极端下跌市场风险95%分位数VaR值之间的VAR模型，可以发现投资者情绪指数的滞后项对自身的当期项有影响，且均在1%的水平下显著，说明投资者情绪指数具有序列相关性1关于投资者情绪指数的序列相关性，在后续的VAR模型中均能得到一致的结论，后文不再赘述。；上证综指极端下跌市场风险95%分位数VaR值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和上证综指极端下跌市场风险95%分位数VaR值之间存在双向的溢出关系，即投资者情绪指数对上证综指极端下跌市场风险95%分位数VaR值存在显著影响，上证综指极端下跌市场风险95%分位数VaR值对投资者情绪指数也存在显著影响。

对于投资者情绪指数和上证综指极端下跌市场风险99%分位数VaR值之间的VAR模型，可以发现上证综指极端下跌市场风险99%分位数VaR值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和上证综指极端下跌市场风险99%分位数VaR值之间存在双向的溢出关系，即投资者情绪指数对上证综指极端下跌市场风险99%分位数VaR值存在显著影响，上证综指极端下跌市场风险99%分位数VaR值对投资者情绪指数也存在显著影响。

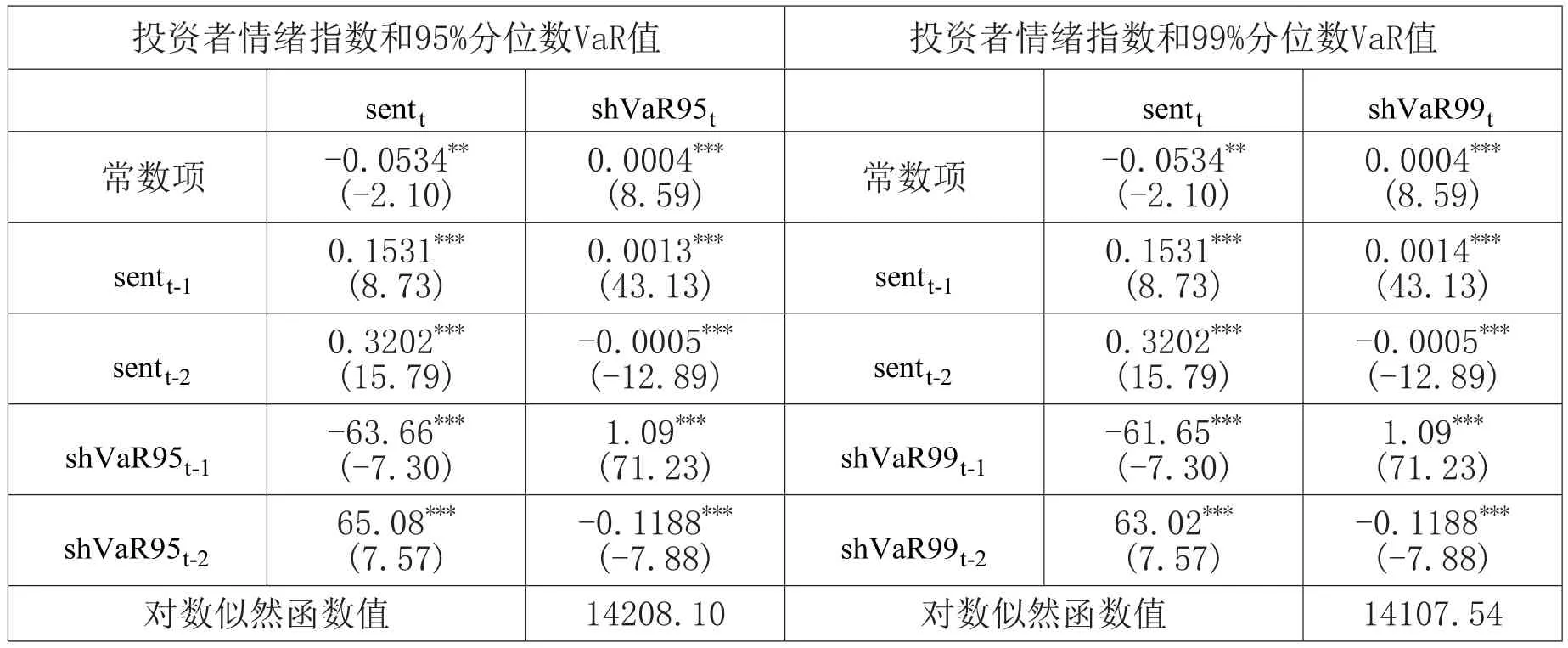
表5 投资者情绪指数与上证综指极端下跌市场风险VaR值之间的VAR模型

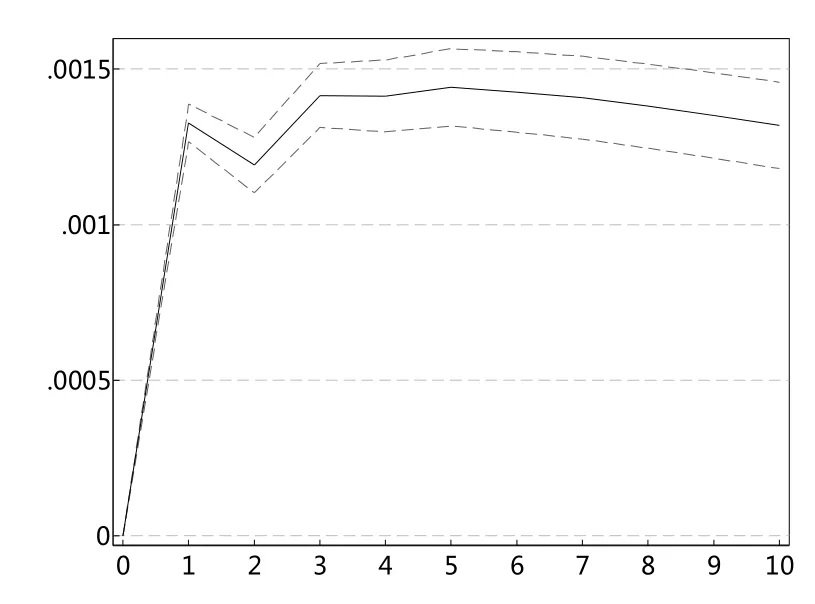
图2 sent对shVaR95冲击图

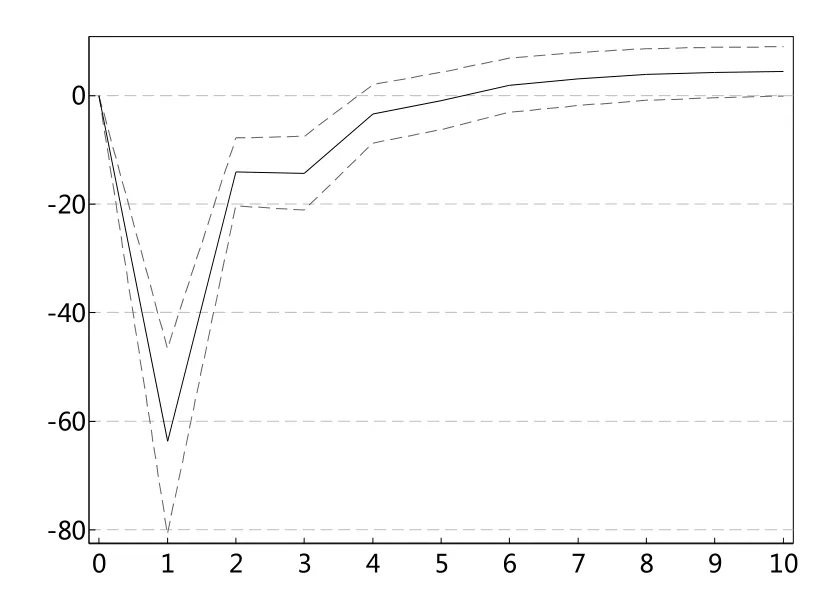
图3 shVaR95对sent冲击图

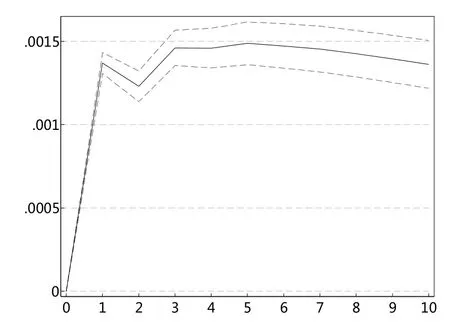
图4 sent对shVaR99冲击图

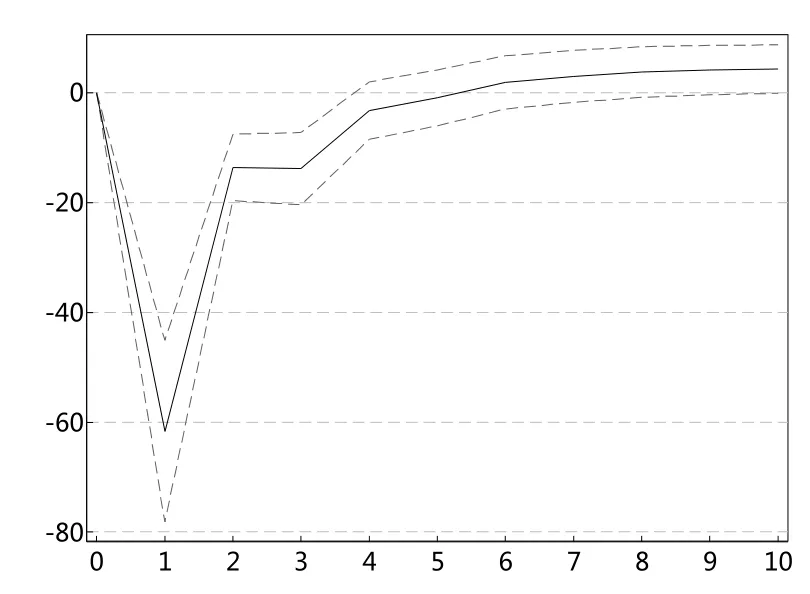
图5 shVaR99对sent冲击图

根据以上的VAR模型结果，本文进一步进行脉冲响应分析。图2和图4一致显示，投资者情绪指数对上证综指极端下跌市场风险VaR值存在显著的冲击，冲击持续扩大至1期，之后趋于稳定。图3和图5表明，上证综指极端下跌市场风险VaR值对投资者情绪指数的冲击在滞后一期达到最大，之后趋于减弱。

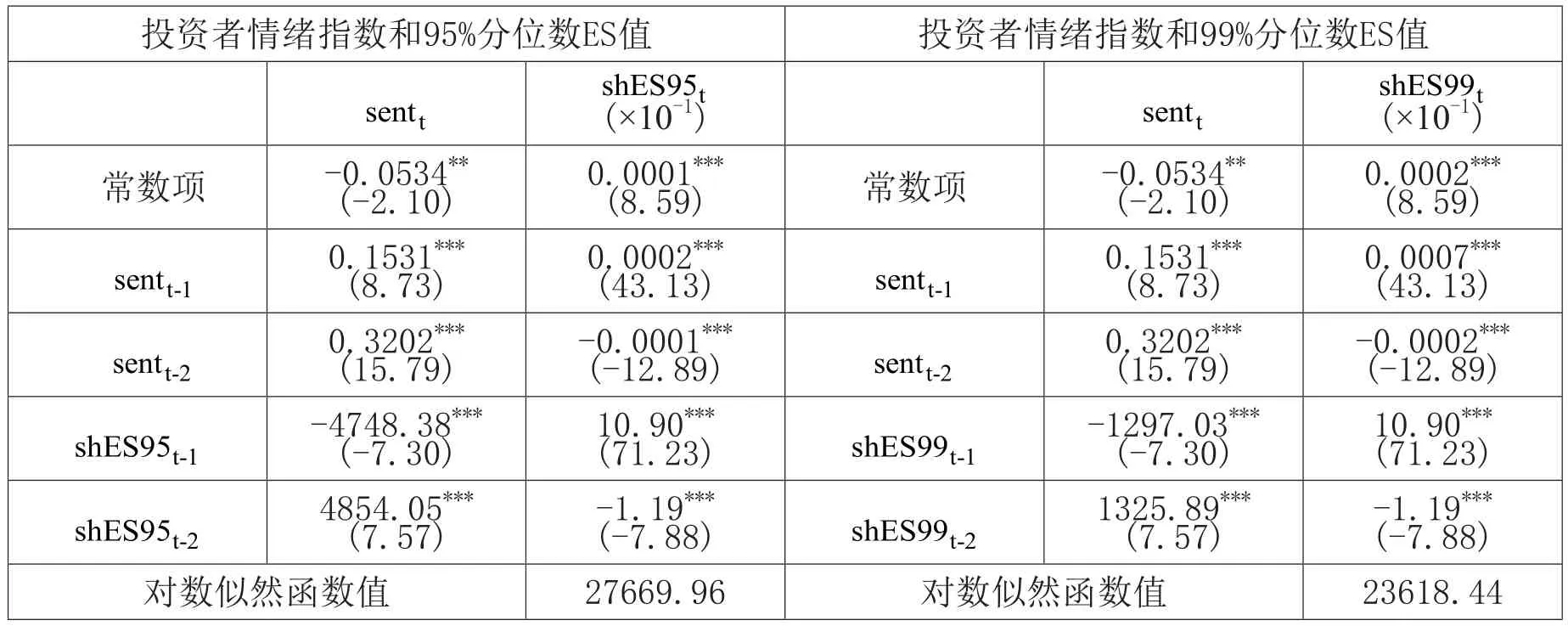
表6 投资者情绪指数与上证综指极端下跌市场风险ES值之间的VAR模型

表6报告了投资者情绪指数和上证综指极端下跌市场风险ES值之间的VAR模型的估计结果。在VAR模型中，本文根据AIC和BIC信息准则得到VAR模型的最优滞后阶数均为2阶。

对于投资者情绪指数和上证综指极端下跌市场风险95%分位数ES值之间的VAR模型，可以发现上证综指极端下跌市场风险95%分位数ES值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和上证综指极端下跌市场风险95%分位数ES值之间存在双向的溢出关系，即投资者情绪指数对上证综指极端下跌市场风险95%分位数ES值存在显著影响，上证综指极端下跌市场风险95%分位数ES值对投资者情绪指数也存在显著影响。

对于投资者情绪指数和上证综指极端下跌市场风险99%分位数ES值之间的VAR模型，可以发现上证综指极端下跌市场风险99%分位数ES值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和上证综指极端下跌市场风险99%分位数ES值之间存在双向的溢出关系，即投资者情绪指数对上证综指极端下跌市场风险99%分位数ES值存在显著影响，上证综指极端下跌市场风险99%分位数ES值对投资者情绪指数也存在显著影响。

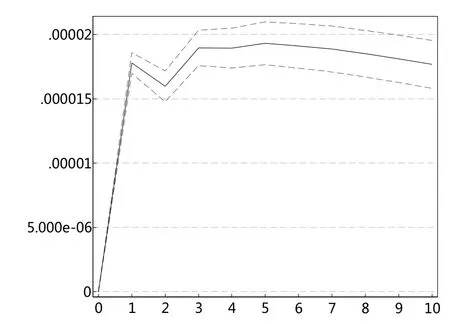
图6 sent对shES95冲击图

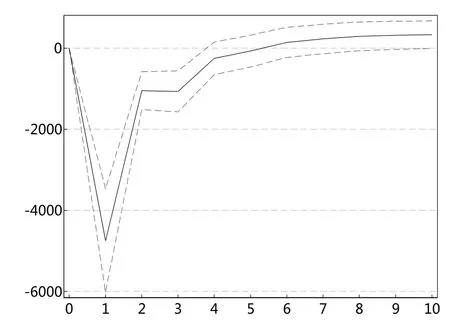
图7 shES95对sent冲击图

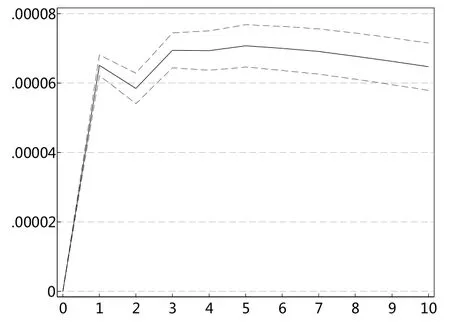
图8 sent对shES99冲击图

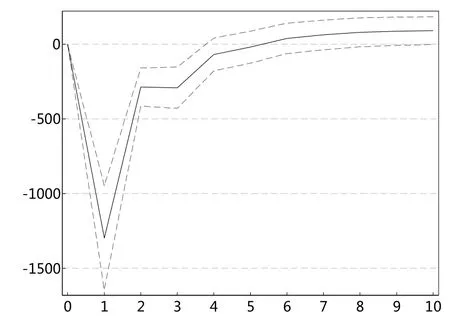
图9 shES99对sent冲击图

根据以上的VAR模型结果，本文进一步进行脉冲响应分析。图6和图8一致显示，投资者情绪指数对上证综指极端下跌市场风险ES值存在显著的冲击，冲击持续扩大至1期，之后趋于稳定。图7和图9表明，上证综指极端下跌市场风险ES值对投资者情绪指数的冲击在滞后一期达到最大，之后趋于减弱。

表7报告了投资者情绪指数和深证成指极端下跌市场风险VaR值之间的VAR模型的估计结果。在VAR模型中，本文根据AIC和BIC信息准则得到VAR模型的最优滞后阶数均为2阶。

对于投资者情绪指数和深证成指极端下跌市场风险95%分位数VaR值之间的VAR模型，可以发现深证成指极端下跌市场风险95%分位数VaR值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和深证成指极端下跌市场风险95%分位数VaR值之间存在双向的溢出关系，即投资者情绪指数对深证成指极端下跌市场风险95%分位数VaR值存在显著影响，深证成指极端下跌市场风险95%分位数VaR值对投资者情绪指数也存在显著影响。

对于投资者情绪指数和深证成指极端下跌市场风险99%分位数VaR值之间的VAR模型，可以发现深证成指极端下跌市场风险99%分位数VaR值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和深证成指极端下跌市场风险99%分位数VaR值之间存在双向的溢出关系，即投资者情绪指数对深证成指极端下跌市场风险99%分位数VaR值存在显著影响，深证成指极端下跌市场风险99%分位数VaR值对投资者情绪指数也存在显著影响。

根据以上的VAR模型结果，本文进一步进行脉冲响应分析。图10和图12一致显示，投资者情绪指数对深证成指极端下跌市场风险VaR值存在显著的冲击，冲击持续扩大至1期，之后趋于稳定。图11和图13表明，深证成指极端下跌市场风险VaR值对投资者情绪指数的冲击在滞后一期达到最大，之后趋于减弱。

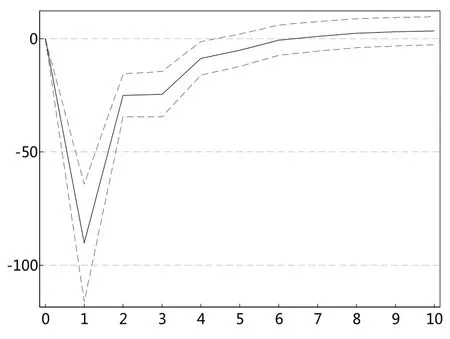
图11 szVaR95对sent冲击图

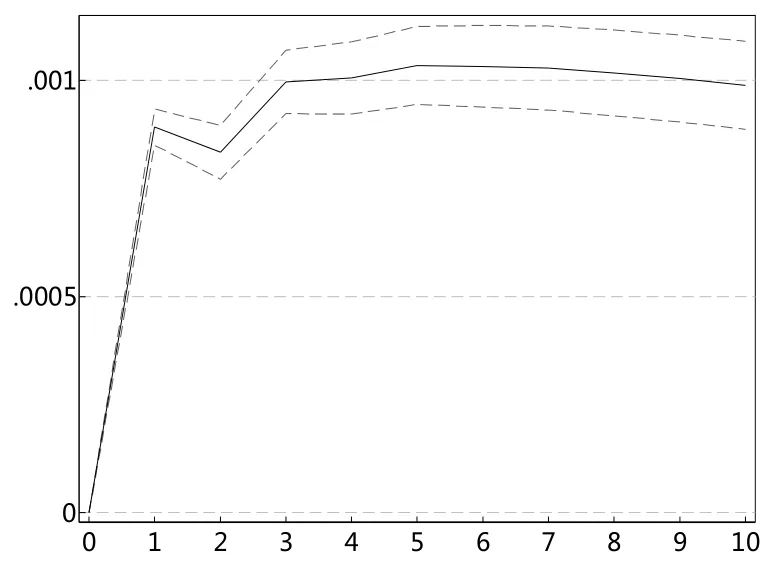
图12 sent对szVaR99冲击图

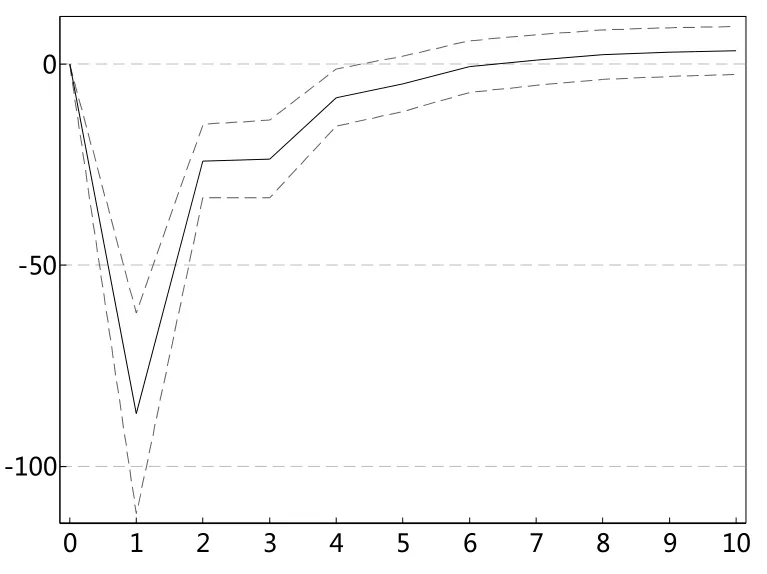
图13 szVaR99对sent冲击图

表8报告了投资者情绪指数和深证成指极端下跌市场风险ES值之间的VAR模型的估计结果。在VAR模型中，本文根据AIC和BIC信息准则得到VAR模型的最优滞后阶数均为2阶。

对于投资者情绪指数和深证成指极端下跌市场风险95%分位数ES值之间的VAR模型，可以发现深证成指极端下跌市场风险95%分位数ES值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和深证成指极端下跌市场风险95%分位数ES值之间存在双向的溢出关系，即投资者情绪指数对深证成指极端下跌市场风险95%分位数ES值存在显著影响，深证成指极端下跌市场风险95%分位数ES值对投资者情绪指数也存在显著影响。

对于投资者情绪指数和深证成指极端下跌市场风险99%分位数ES值之间的VAR模型，可以发现深证成指极端下跌市场风险99%分位数ES值的滞后项对当期项有影响，且均在1%的水平下显著，说明其具有序列相关性；在两个回归方程中，交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和深证成指极端下跌市场风险99%分位数ES值之间存在双向的溢出关系，即投资者情绪指数对深证成指极端下跌市场风险99%分位数ES值存在显著影响，深证成指极端下跌市场风险99%分位数ES值对投资者情绪指数也存在显著影响。

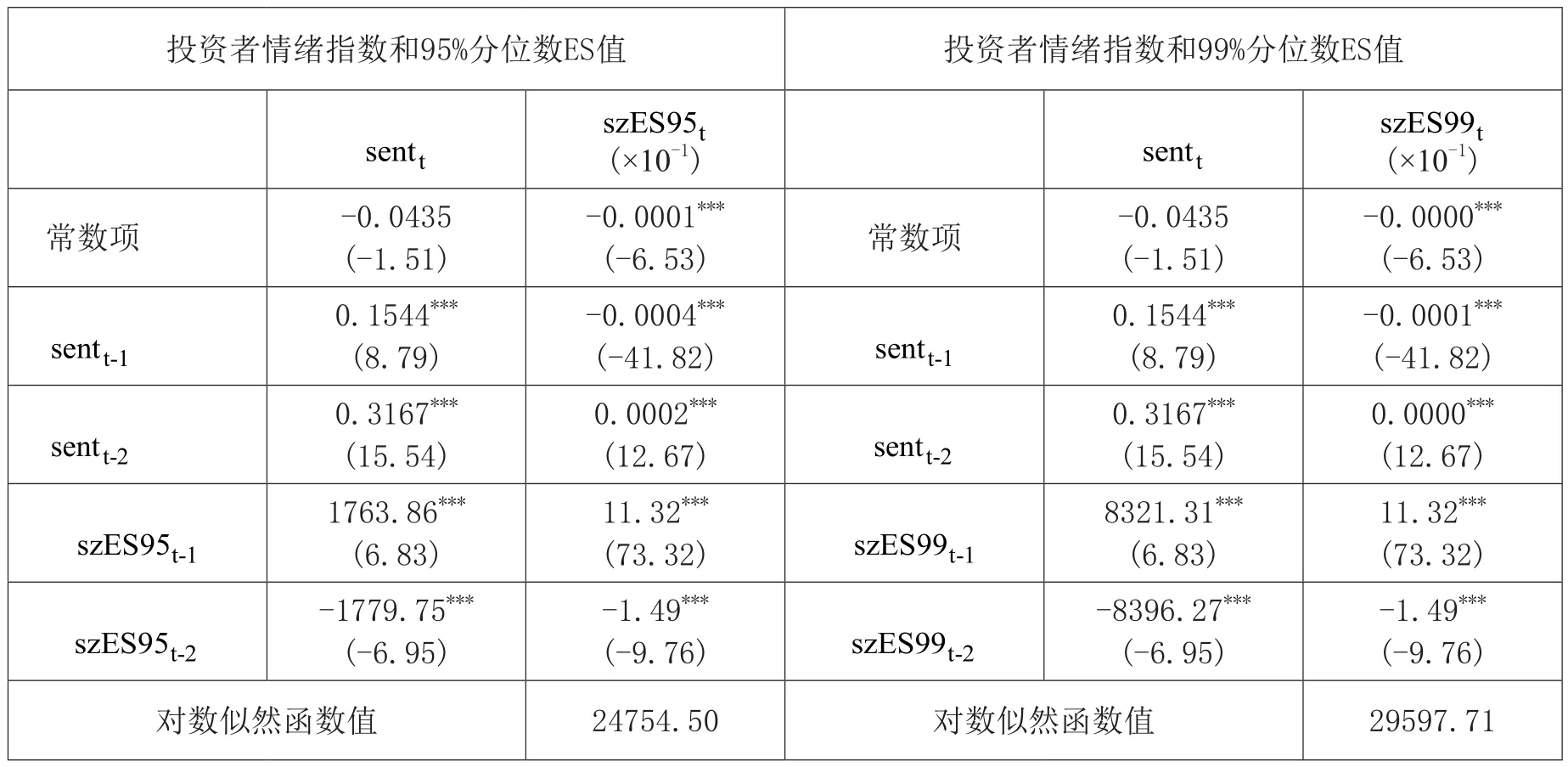
表8 投资者情绪指数与深证成指极端下跌市场风险ES值之间的VAR模型

根据以上的VAR模型结果，本文进一步进行脉冲响应分析。图14和图16一致显示，投资者情绪指数对深证成指极端下跌市场风险ES值存在显著的冲击，冲击持续扩大至1期，之后趋于稳定。图15和图17表明，深证成指极端下跌市场风险ES值对投资者情绪指数的冲击在滞后一期达到最大，之后趋于减弱。

(四)投资者情绪与不同风格资产的极端下跌市场风险

依据申万风格指数分类，本文测度了大盘股、中盘股、小盘股与高市净率股、中市净率股、低市净率股95%分位数极端下跌市场风险的VaR值和ES值，再基于VAR模型对投资者情绪与不同风格资产的极端下跌市场风险之间的关联进行分析。在VAR模型回归之前，本文对相关变量进行了ADF检验，发现它们均是平稳序列。根据AIC和BIC信息准则，得到VAR模型的最优滞后阶数均为2阶。

表9和表10报告了投资者情绪指数与不同市值股票极端下跌市场风险VaR值和ES值的VAR模型回归结果。从中可以看出，投资者情绪指数和极端下跌市场风险的滞后项对当期项有影响，且均在1%的水平下显著，说明它们均具有序列相关性。

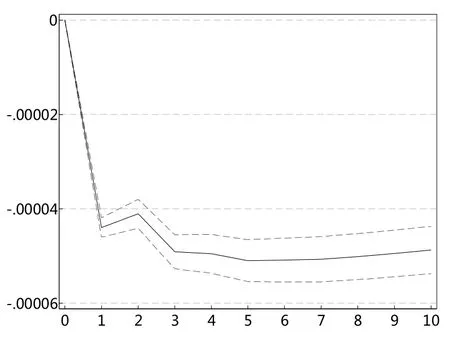
图14 sent对szES95冲击图

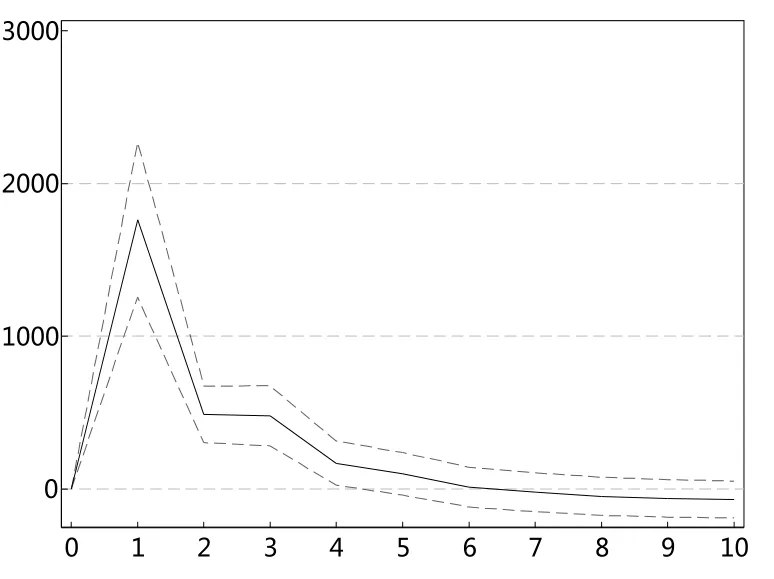
图15 szES95对sent冲击图

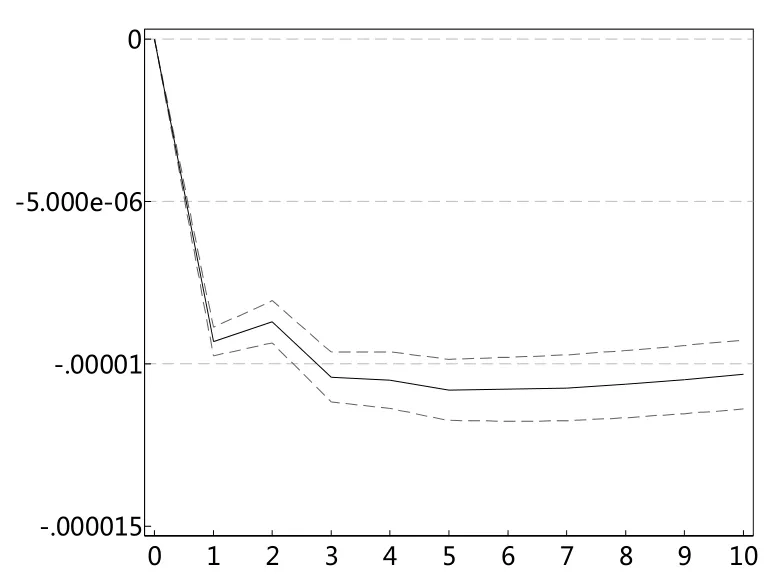
图16 sent对szES99冲击图

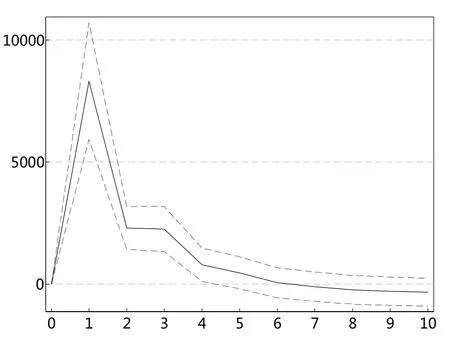
图17 szES99对sent冲击图

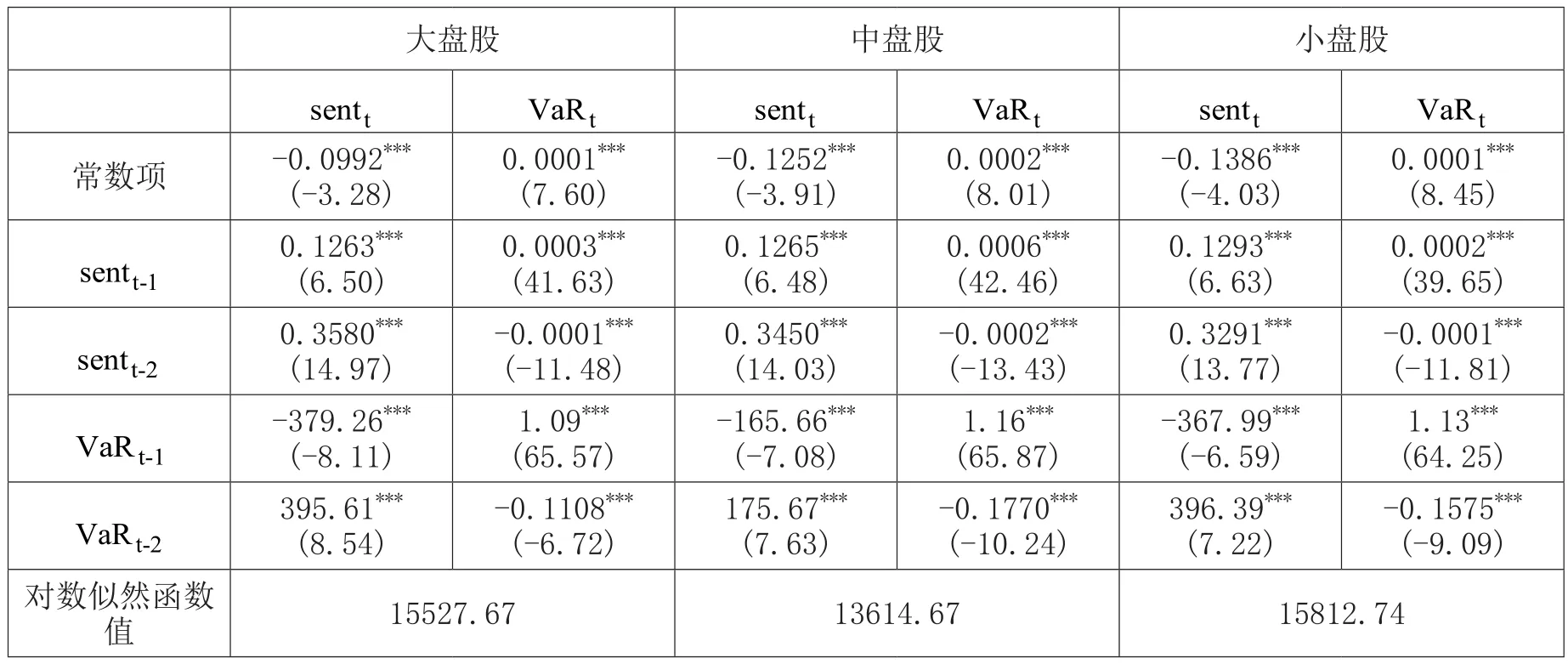
表9 投资者情绪指数与不同市值股票极端下跌市场风险VaR值之间的VAR模型

表10 投资者情绪指数与不同市值股票极端下跌市场风险ES值之间的VAR模型

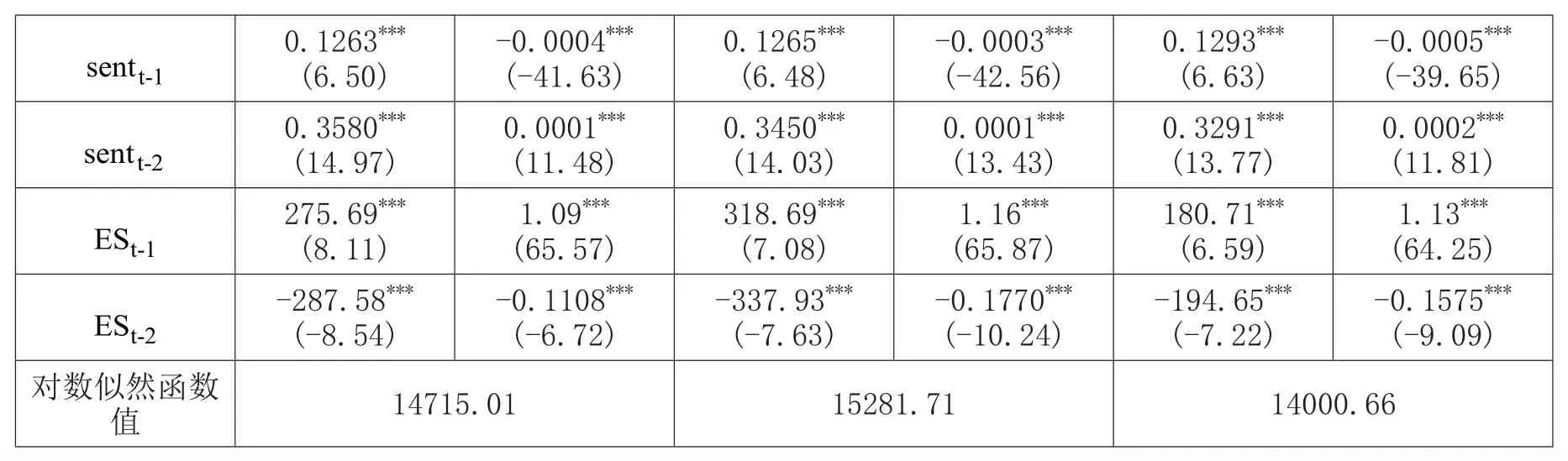
注：括号中数字为估计系数的t值；*、**、***分别表示在 10%、5%和 1%的水平上显著。

交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和极端下跌市场风险之间存在双向的溢出关系。不同市值股票之间，大盘股的极端下跌市场风险VaR值对投资者情绪的影响最大，小盘股的极端下跌市场风险ES值对投资者情绪的影响最小，说明大盘股相对于小盘股，其极端市场风险更能影响投资者情绪；投资者情绪对小盘股的极端下跌市场风险VaR值影响最小，而投资者情绪对小盘股的极端下跌市场风险ES值影响最大，造成这种差异的原因可能在于ES值在度量极端风险方面优于VaR值。

表11和表12报告了投资者情绪指数与不同市净率股票极端下跌市场风险VaR值和ES值的VAR模型回归结果。从中可以看出，投资者情绪指数和极端下跌市场风险的滞后项对当期项有影响，且均在1%的水平下显著，说明它们均具有序列相关性。交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和极端下跌市场风险之间存在双向的溢出关系。不同市净率股票之间，高市净率股票的极端下跌市场风险VaR值和ES值对投资者情绪的影响相对较小，说明高市净率股票的极端市场风险对整体市场投资者情绪的影响力较小；相对于高市净率股票，投资者情绪对低市净率股票的极端下跌市场风险影响较小。

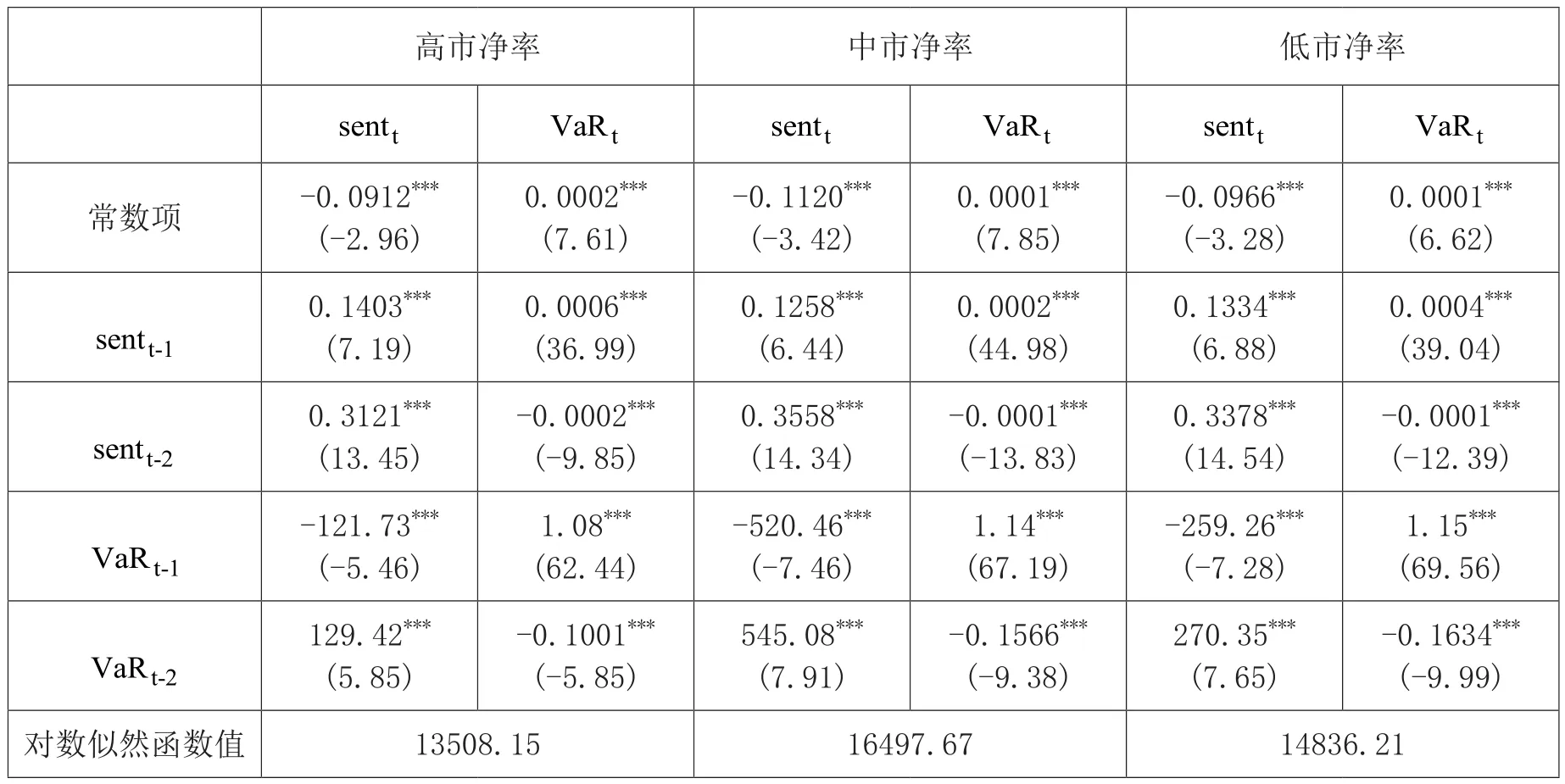
表11 投资者情绪指数与不同市净率股票极端下跌市场风险VaR值之间的VAR模型

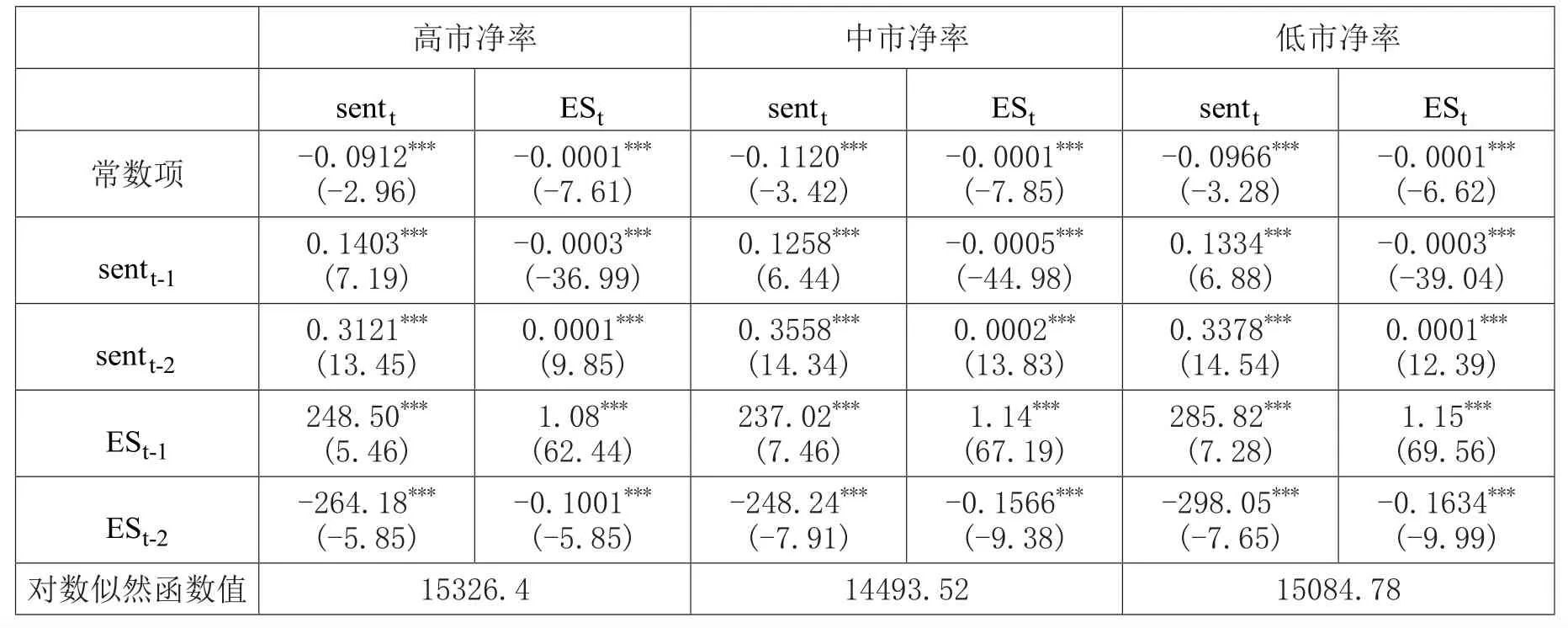
表12 投资者情绪指数与不同市净率股票极端下跌市场风险ES值之间的VAR模型

五、结论

本文选取中国股市流动性、换手率、腾落比例及新高新低指标作为投资者情绪代理指标，采用主成分分析法提取共同的投资者情绪成分，构建投资者情绪指数。然后，运用POT模型来度量极端市场风险，分别计算极端风险测度的VaR值和ES值。最后，本文使用VAR模型研究投资者情绪和极端市场风险之间的关系。研究得到以下结论：

第一，投资者情绪指数和极端市场风险的滞后项对当期项有影响，且均在1%的水平下显著，说明它们均具有序列相关性。

第二，投资者情绪指数和极端市场风险的交叉滞后项的系数均在1%的水平下显著，说明投资者情绪指数和极端市场风险之间存在双向的溢出关系。

第三，相对于小盘股，大盘股的极端市场风险更能影响投资者情绪，而投资者情绪对小盘股的极端市场风险影响最大；相对于高市净率股票，投资者情绪对低市净率股票的极端下跌市场风险影响较小，而高市净率股票的极端市场风险对整体市场投资者情绪的影响力较小。

本文不仅有助于更好认识极端市场风险的生成机理，而且对防范市场风险、维护金融安全和稳定有一定的启示。