SPH-FEM耦合方法在弹丸膛内运动中的应用

孙玉杰，崔青春，丁宏民，徐 坚，郭俊行

(西北机电工程研究所，陕西 咸阳 712099)

由于火炮发射时间短，载荷脉冲峰值大，且弹丸在密闭的身管空间内运动，参数不易测量，试验又难以复现火炮发射环境，发射动力学成为一种可能的分析方法，用物理模型去复现火炮发射过程中各物理参量的变化情况。文献[1]采用自适应网格技术(Arbitrary Lagrangian-Eulerian，ALE)，解决挤进过程中弹丸网格因大变形而发生的网格畸变问题，通过仿真获得了弹丸挤进过程中变形及残余应力变化。文献[2]对某大口径榴弹炮发射条件下弹带挤进过程中的弹带动态挤进阻力、挤进压力、弹带大变形和弹丸运动规律进行了数值模拟研究。文献[3]建立航空自动炮的热力耦合有限元模型，采用Fortran子程序结合显式有限元方法对弹带挤进及内弹道过程进行了研究，获得了次要功系数随时间变化并存在极值，弹带表层受热软化对内弹道过程有显著影响等结论。文献[4-5]采用显式动力学的方法对弹带挤进过程进行了分析，分析了坡膛结构变化对内弹道性能和坡膛受力状态的影响。文献[6-7]采用显式动力学建立弹带挤进的热力耦合模型，将挤进时期的内弹道方程作为力学边界条件，并采用改进库伦摩擦模型，得到了挤进过程中挤进阻力、弹丸速度、膛压和弹丸摆角的变化规律。文献[8]采用光滑粒子与有限元耦合的方法对某大口径火炮弹丸挤进过程进行数值模拟，获得了挤进过程中弹带材料的塑性流动及应力应变变化。文献[9]建立了将内弹道计算与弹头发射过程有限元计算相耦合的模型，并考虑了枪管的弯曲，获得了弹头受力及枪口振动情况。文献[10]建立了预制刻槽弹带与身管的弹炮耦合火炮发射动力学模型，模型中实现了火药燃气压力随弹丸运动而动态变化的分布。上述弹炮耦合研究中：有仅对弹丸挤进过程进行了研究；有弹带预制刻槽，忽略挤进过程；有对小口径弹丸全膛运动进行了研究。一方面挤进和直膛运动是个连续过程；另一方面大口径火炮与小口径火炮在身管内膛和弹丸结构等方面差异较大，上述研究不能直接应用于大口径火炮全膛运动分析。

大口径火炮弹丸全膛运动过程中，弹带经历侵彻、挤压，发生大的塑性变形和材料失效。对该问题的模拟，传统的基于网格的有限元存在单元畸变，导致计算精度和效率下降，甚至无法完成有效的计算。针对传统FEM(Finite Element Method)的局限性，SPH(Smoothed Particle Hydrodynamics)等无网格技术应运而生，SPH法以一种拉格朗日形式的无网格粒子代替网格单元，粒子携带着物质的材料特性和力学量信息，具有良好的自适应性，克服了FEM由于产生大变形畸变而终止计算这一难题，在处理侵彻、穿甲等大变形问题上极具优势。但SPH算法相比传统有限元方法，存在计算效率低，且不易施加边界条件。大口径火炮弹丸全膛运动过程中，只有弹带发生大的塑性变形和材料失效。而整个发射系统其它部分发生刚体运动和小的弹性变形。故对大变形的弹带采用SPH粒子模拟，发射系统的其它结构采用FEM建模，通过FEM-SPH耦合算法实现结构相互间的力学行为传递，该方法结合了SPH方法处理大变形能力和FEM的计算效率高的互补优势。

本文采用有限元和光滑粒子耦合方法，研究某大口径火炮弹丸全膛运动过程，获得弹带温度变化、影响炮口振动因素和弹丸运动姿态的变化，并与试验数据进行对比，验证SPH-FEM模型的有效性。该研究为大口径火炮弹炮匹配设计及精度设计提供了参考。

1 大口径火炮非线性有限元动力学模型

以某大口径履带式自行火炮为研究对象，采用SPH-FEM耦合方法建立了弹炮耦合的大口径火炮非线性有限元动力学模型，分析其在水平地面上静止状态下射击时动力响应。

1.1 各部件拓扑关系

动力学模型中包含弹带、弹丸、身管、炮口制退器、炮尾、摇架、前后铜套、定向栓、炮塔、座圈、底盘、悬挂和履带等。模型中各部件拓扑关系如图1所示。hi(i=1～38)为部件间的连接关系。其中：弹丸与弹带为绑定连接(h1)；弹丸定心部、弹带与身管内膛间为接触作用(h2，h3)；炮口制退器、抽气装置、炮尾闩体与身管间为绑定连接(h4，h5，h7)；身管与前后铜套间为接触作用(h6，h8)；复进机和制退机的后坐部分与炮尾闩体为绑定连接(h9，h10)；炮尾闩体与定向栓间为绑定连接(h11)；前、后铜套与摇架间为绑定连接(h12，h16)；定向栓与摇架定向栓室间为接触作用(h14)；复进机和制退机的非后坐部分与摇架为绑定连接(h13，h15)；高低机主齿轮与摇架齿弧间为接触作用(h17)；摇架和炮塔间为耦合约束关系(h18)，即只释放摇架绕耳轴轴线方向的旋转自由度；平衡机、高低机、上座圈、方向机和炮塔，下座圈和底盘为绑定连接(h20～h22，h26)；上座圈和滚珠、下座圈和滚珠、方向机主齿轮与下座圈内齿圈为接触作用(h23～h25)。扭力轴一端与车体固结，一端与平衡肘通过花键连接(h27，h28)；平衡肘与负重轮、诱导轮与底盘、拖带轮与底盘、主动轮与底盘为耦合约束关系(h29～h32)，即只释放其绕转动中心方向的旋转自由度；负重轮、诱导轮、拖带轮和主动轮与履带内表面为接触作用(h33～h36)；履带外表面与地面为接触作用(h37)。

图1 某大口径履带式自行火炮拓扑关系图Fig.1 Topology relationships of large-caliber artillery

1.2 网格模型

某大口径火炮有限元模型如图2所示。模型中含有粒子单元、实体单元、壳单元、质量单元和连接单元等。总的单元数为1 950 346，总的节点数为2 338 318。坐标原点O位于座圈上平面圆心处，x轴沿水平方向指向炮口，y轴垂直方向向上，z轴根据右手法则确定。

身管膛线为空间曲线，且膛线断面尺寸与身管长度尺寸存在量级差异，利用专业前处理软件的强大网格划分功能，除膛线起始部有楔形单元外，身管其余采用六面体单元，为准确刻画挤进段弹带与身管内膛的相互作用，对膛线起始部进行了网格加密，整个身管包含543 264个单元。身管局部有限元模型如图3所示。

图2 大口径履带式自行火炮有限元模型Fig.2 Finite element model of large-caliber artillery

弹带采用光滑粒子进行离散。有两种方法进行建模，一种为自适应算法，先建立弹带的有限元网格，并定义单元转变粒子准则，当某个单元满足转换准则，该单元转换为粒子；第二种是分析一开始就建立弹带的SPH粒子。由于Abaqus软件对第一种方式的并行有限制要求[11]，为提高计算效率，本文采用第二种方式。所建立的弹带SPH模型如图4所示，弹带粒子单元数为746 916。

图3 身管局部网格模型Fig.3 Partial mesh model of gun barrel

图4 弹带SPH模型Fig.4 SPH model of rotating bands

1.3 材料模型

Johnson-Cook材料模型作为一种理想刚塑性强化模型既可以反映材料在高应变速率下应变硬化、应变速率硬化，又可以反映热软化效应[12]。Johnson-Cook材料模型中屈服应力是塑性应变、应变率以及温度的函数

(1)

T*=(T-Tr)/(Tm-Tr)

(2)

(3)

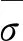
为了获得更加精确的材料参数，开展弹带材料在较宽应变速率和温度范围内力学性能测试，采用Gleeble3500热模拟试验机进行准静态及低应变率下弹带材料压缩试验；采用带温度控制装置的分离式霍普金森压杆装置进行弹带材料高应变率下压缩试验。通过对试验数据处理，回归得到Johnson-Cook方程的各个材料参数为：A=133 MPa，B=324 MPa，C=0.043，m=1.21和n=0.48。图5为黄铜材料在3 000 s-1应变速率下应力-应变关系试验测量值与Johnson-Cook模型预测值对比，从图中可以看出，预测结果均与试验值吻合较好。

图5 3 000 s-1应变率下应力-应变关系试验值与预测值对比Fig.5 Comparison of stress-strain curves between experimental measurements and predictions under 3 000 s-1 strain rate

(4)

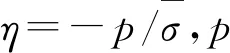
身管为炮钢材料，前后铜套为铸造铝青铜，其它部件材料为合金钢，靶场地面为混凝土，对应的材料参数如表1所示。

表1 动力学模型中材料参数Tab.1 Material parameters of dynamical model

1.4 弹带与身管内膛摩擦界面特性

弹带与身管内膛的摩擦界面特性对于弹丸启动压力、弹丸膛内运动，身管内膛损伤有重要影响。借鉴在高速切削以及摩擦搅拌焊接研究中，切向摩擦行为多采用修正的库伦摩擦模型来表征接触面之间高速重载的摩擦特性。切接触面的切向应力由式(5)决定

(5)

式中：f为切向应力，MPa；μ为静摩擦因数，取为0.13；σn为正压力，MPa；τs为弹带材料的随温度变化的剪切极限，MPa，取为

(6)

弹丸弹带和弹丸定心部与膛线的接触和碰撞状态，通过平衡主控—从属搜索算法进行计算。

1.5 载荷、边界条件处理

火炮发射时，作用于发射系统的载荷有膛底压力、弹底压力、波尔登力、制退机力、复进机力和平衡机力等。动力学模型中采用电子测压弹获得实弹射击时的膛底压力，并由文献[14]第“3～5”节所述内弹道计算中应用的压力换算关系，换算得到弹底压力。由于温度分布不均匀和重力的作用，身管在发射前向下弯曲。火炮发射时，膛内高压火药气体的作用必然使弯曲的身管产生波尔登效应，即弯曲的身管在发射时受到波尔登力的作用。随着现代火炮身管长度的增加，波尔登载荷对弹丸膛内运动和炮口振动的影响不可忽略。通过子程序VDLOAD在弹后空间施加拉格朗日分布的压力来模拟波尔登力的影响。复进机力通过在复进机与炮尾和摇架的连接点上施加一对共线且反向的随时间变化的集中力来模拟[15]。制退机力和平衡机力也采用相同的方法。其随时间变化通过相应的计算书获得。火炮静止状态下射击，主动轮制动，约束其转动自由度。

2 火炮发射动力学模型仿真分析

弯曲身管将改变弹丸在膛内的运动状态，为准确获得火炮发射过程中的动态响应，采用隐式、显式联合求解的方法，充分利用两种求解器的优势。先采用隐式求解器获得火炮发射动力学模型在重力载荷作用下的静变形及等效应力，起落部分垂直方向最大变形量发生在炮口制退器处，大小约为10.6 mm，最大等效应力位置位于平衡机处，大小约为320 MPa，如图6所示。然后将此状态作为火炮发射动力学模型的初始构型，重新设定约束状态、载荷等，利用显式求解器对发射过程的动态响应进行求解。分别在引信质心和弹丸质心处设置两个参考点，分别与少数单元设置刚体约束。定义两参考点的连线与弹丸质心处的速度矢量之间的夹角为弹丸章动角，其单位为 °。

图6 动力学模型在重力载荷作用下的响应Fig.6 Response of dynamics model under the gravity load

2.1 火炮发射动力学模型验证

通过高速摄影的标记点与动力学模型中的对应位置的位移进行比较，来验证所建立动力学模型的准确性。从图7(a)可以得出：计算值与测量值变化趋势相同，膛内时期处于加速后坐过程，后坐速度逐渐增大，故后坐位移曲线外凸。出炮口时刻后坐位移约为115 mm。从图7(b)可以得出：垂直于身管方向位移的计算值与测量值变化趋势相同，4 ms前，由于弹丸处于挤进过程，此时身管扭转刚度很大，加上弹丸转速低，弹炮作用不强烈，垂直于身管方向位移几乎为零。随着弹丸向前运动，身管扭转刚度减小，加上弹炮相互作用强烈，垂直于身管方向位移逐渐增大，一直到弹带出炮口前，达到最大值。当弹带出炮口后，由于弹带对身管扭转作用消失，身管有一定的回复。

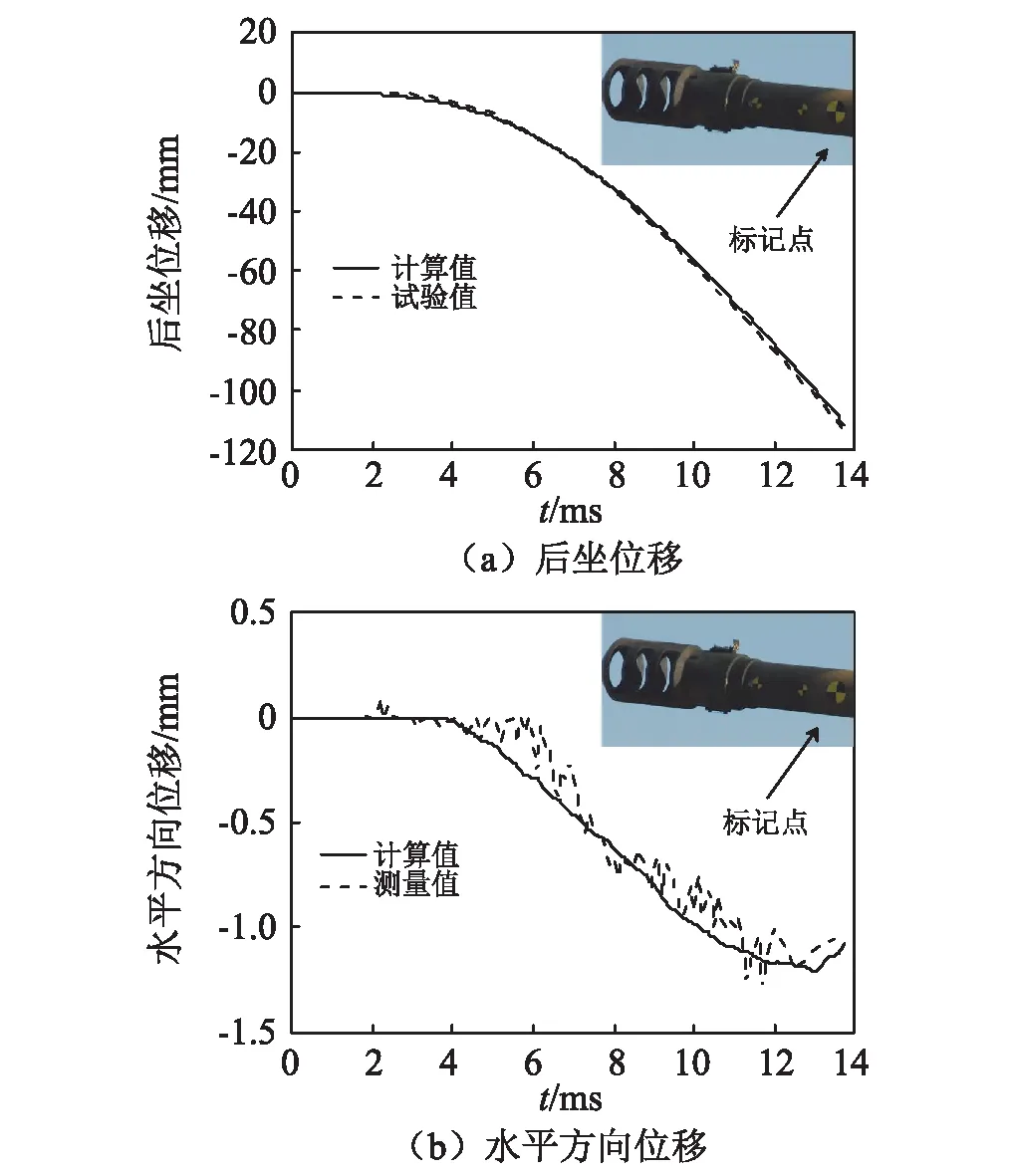
图7 动力学模型计算结果与高速摄影测量值对比Fig.7 Comparisons between simulation results and high-speed video measurements

2.2 火炮发射动力学模型结果分析与讨论

2.2.1 计算效率分析

显式时间积分的稳定步长近似估计为

(7)

式中：Δtmin为稳定步长，s；lmin为单元最小边长，mm；E为弹性模量，MPa；ρ为密度，kg/m3；ν为泊松比。

弹带采用ALE时，由于弹带在挤进过程中和随后的直膛运动过程中，发生大变形，造成单元畸变，特征长度减小，造成稳定步长变小，从而大大增加求解时间。而弹带采用SPH时，稳定步长随弹带发生变形而减小的程度较小，从而保证了较高的计算效率。图8为显式动力学模型中稳定步长随时间变化。从图中可以看出，采用SPH时稳定步长在4.4×10-8～4.64×10-8s。

图3列出了连续神经网络算法在空手道俱乐部网络上的仿真结果。从实验结果发现，特征向量算法、连续算法对空手道俱乐部网络的分类结果与特征向量算法的分类结果（Q=0.3715）相同，表明本文中的算法也是合理的。

图8 稳定步长随时间变化曲线Fig.8 Curve of stable time increment with time

2.2.2 膛内运动弹带温度

获得弹丸在膛内不同时期弹带温度变化，如图9所示。挤进过程中，弹带发生大的塑性变形，塑性功占主导，塑性功转变为内能，弹带温度升高。挤进完成后，随着弹丸速度增加，摩擦阻力做功占主导，摩擦阻力做功转变为内能，使得弹带与膛线紧密贴合部位温度继续升高。挤进初期弹带温度云图如图9(a)所示，最高温度为102 ℃。前弹带挤进完成时，弹带温度云图如图9(b)所示，最高温度为457 ℃。挤进完成时，弹带温度云图如图9(c)所示，最高温度约为585 ℃，这与文献[16]研究相符，挤进完成，弹带表面温度超过再结晶温度280 ℃，但未达到熔点。最大膛压点时，弹带温度云图如图9(d)所示，最高温度为636 ℃。弹丸行程一半时，弹带温度云图如图9(e)所示，最高温度为846 ℃。弹丸进入半约束期时，弹带温度云图如图9(f)所示，最高温度为1 033 ℃。由图9还可以得出：弹丸膛内运动，弹带表层温度逐渐升高，弹带表层甚至达到材料的熔点，弹带与身管间建立了熔融润滑，滑动机理变为流体动力润滑滑动[17]，由于作用时间短，热量来不及向弹带内部传导，弹带内部仍然为初始温度，弹带形成软硬结合的结构，造成摩擦因数减小。

图9 弹丸运动不同位置弹带温度分布云图Fig.9 Contour of rotating band temperature distribution at different locations

2.2.3 影响炮口运动因素分析

火炮发射过程中，受力复杂，各种因素对炮口运动相互影响，且同时发生，采用试验测试很难区分其单独的影响，发射动力学成为一种可能的方法去区分各个因素对炮口点运动的影响。采用所建立的模型分别计算后坐运动、后坐运动中计及波尔登力、后坐运动中计及弹炮耦合和后坐运动中计及波尔登力和弹炮耦合四种工况。为描述炮口振动，定义炮口中心点与炮口制退器前端面耦合，输出其在整个发射过程中的位移变化，耦合示意图如图10所示。各工况下炮口点的运动如图11所示，图11(a)为炮口点垂直方向位移，图11(b)为炮口点水平方向位移。

图10 炮口点耦合示意图Fig.10 The illustration of the coupling between reference point and muzzle

垂直方向：该火炮后坐部分质心在炮膛轴线下方，膛内期，由于动力偶臂的作用，起落部分发生俯仰运动，炮口点位移向上；由于重力作用，身管初始构型向下弯曲，则波尔登力有使身管变直的趋势，后坐运动也使垂直方向位移向上，两者综合作用使得炮口点位移向上。曲线的振荡是由于膛压移动导致；9 ms之前由于弹丸与身管的作用不强烈，和后坐运动计算结果基本相同。此后弹丸定心部与身管内膛的接触碰撞加剧，影响炮口点的振动。11.6 ms前，计及波尔登力和弹炮耦合与考虑波尔登力时两者变化一致，此后由于弹丸前定心部与身管内膛的碰撞加剧，影响炮口位移。波尔登力和弹炮作用对垂直方向位移影响显著。

图11 不同因素对炮口点位移影响Fig.11 The effect of different factors on muzzle displacement

垂直方向：由于身管初始构型在水平方向变形量很小，波尔登力作用不如垂直方向显著，引起的位移很小；4 ms之前，位移为零，此后由于弹丸和身管的相互作用引起位移在零点附近跳动，随着弹丸前定心部与身管内膛的碰撞加剧，水平方向位移变化增大。水平方向位移主要受弹炮作用影响，且水平方向位移小于垂直方向位移。

2.2.4 弹丸不平衡因素的影响

由第“2.2.3”节分析可知，弹炮作用对于炮口点垂直方向和水平方向位移都有显著影响。膛内期，弹丸约逆时针旋转2.2圈(从炮口看向炮尾)，出炮口时弹丸质量偏心方位与卡膛时质量偏心方位恒相差约72°。当卡膛时质量偏心方位位于象限点1上，出炮口时质量偏心方位位于左上方1*处，箭头所示方向为弹丸旋转方向，如图12所示。炮口点在Y-Z面的位移轨迹分布在第一、二象限内，膛内运动前期，弹丸转速较低，弹炮作用不强烈，曲线重合，随着转速增大，质量偏心大的，惯性离心力也大，曲线分离。图13为膛内弹丸章动角随时间变化，膛内运动前期，章动角幅值较小，但变化较快，随后的直膛内运动，章动角幅值变大，出炮口时达到最大值，质量偏心影响明显，零偏心时0.068 37 °增大至偏心0.2 mm时0.138 33 °，章动角几乎增大两倍。

弹丸装填时，质量偏心方位在整个圆周范围内随机分布。分析弹丸质量偏心为0.2 mm，质量偏心分别位于四个象限点上时炮口点振动和章动角的变化。从图15可以看出：弹丸质量偏心方位相位差为90°，则弹炮作用的方位也相差90°，出炮口时位移也基本上相差90°，质量偏心方位对炮口点的振动影响显著，如图14所示。当质量偏心方位位于2位置时，弹丸膛内时期章动角幅值最大，质量偏心方位位于4位置时，弹丸膛内时期章动角幅值最小，如图15所示。

2.2.5 初始装填姿态的影响

上述模型中，弹丸几何轴线与身管轴线平行。由于装填误差等原因，装填到位后，弹丸轴线与身管轴线不完全重合，也就是两者之间有一定的夹角。分析质量偏心为0.1 mm，卡膛时质量偏心位于象限点1上，卡膛角取为仰4′、仰2′、0′、俯2′和俯4′(仰为铅垂面内，弹轴在身管轴线上方，并与之相交；反之定义为俯)。由于铅垂面内，身管向下弯曲，身管内膛约束弹丸沿其轴线运动，当卡膛角为仰时，炮口点的振动变化相同，当卡膛角为俯时，也有相似变化，如图16所示。随着装填角度的增大，弹丸的章动角波动范围变大，出炮口时，仰4′相对于0′，章动角增大2.08倍。当卡膛角为俯时，出炮口时，仰4′相对于0′，章动角增大1.7倍。相同卡膛角时，卡膛角为俯时，无论章动角的最大值还是出炮口时相应值都大于卡膛角为仰时，如图17所示。

图12 相同偏心方位不同质量偏心对炮口点振动的影响Fig.12 The effect of mass eccentricity on the vibration of muzzle under the same orientation of mass eccentricity

图13 相同偏心方位不同质量偏心对章动角的影响Fig.13 The effect of mass eccentricity on the nutation angle of projectile under the same orientation of mass eccentricity

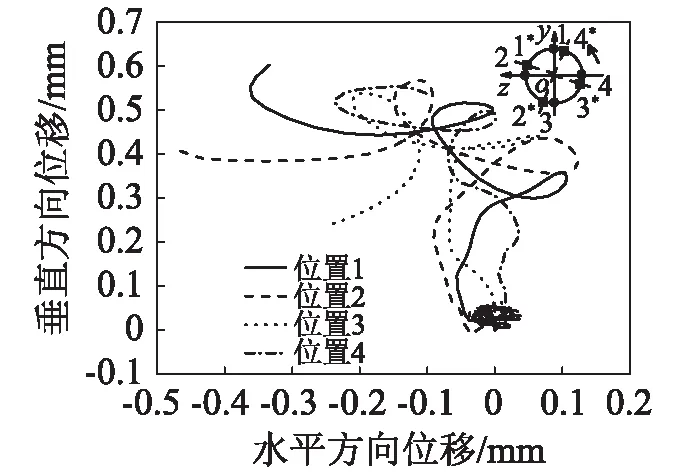
图14 相同质量偏心不同质量偏心方位对炮口点振动的影响Fig.14 The effect of the orientation of mass eccentricity on the vibration of muzzle under the same mass eccentricity

图15 相同质量偏心不同质量偏心方位对章动角的影响Fig.15 The effect of the orientation of mass eccentricity on the nutation angle of projectile under the same mass eccentricity

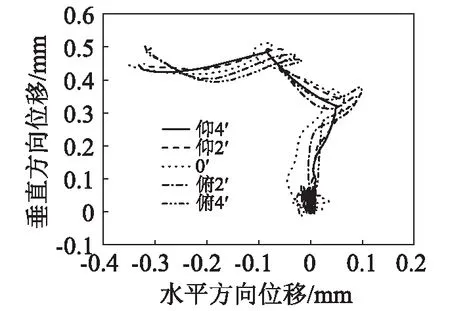
图16 不同初始装填姿态对炮口点振动的影响Fig.16 The effect of the initial loading posture on the vibration of muzzle

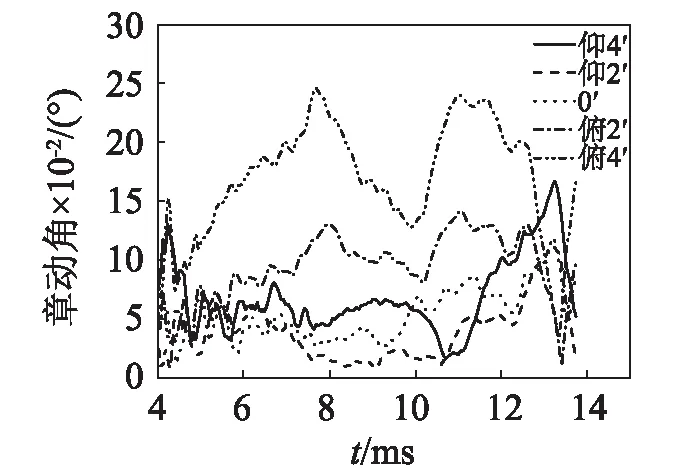
图17 不同初始装填姿态对章动角的影响Fig.18 The effect of the initial loading posture on the nutation angle of projectile

3 结 论

(1)针对大口径火炮弹丸全膛运动过程中因为弹带高速侵彻和挤压导致网格畸变而使计算效率低的问题，弹带采用SPH模拟，火炮其它结构采用FEM模拟，通过FEM-SPH耦合的方法实现结构相互间的力学行为传递。即利用了SPH处理大变形优势，又充分利用了FEM计算精度高的特性。

(2)弹丸膛内运动过程中，由于弹带发生塑性变形和摩擦力做功，挤进完成后弹带表面超过再结晶温度；随后的膛内运动中，弹带表面温度接近熔点。

(3)波尔登力和弹炮作用对炮口点垂直方向位移影响显著；水平方向位移主要受弹炮作用影响，且水平方向位移小于垂直方向位移。

(4)质量偏心和质量偏心方位对于炮口点运动影响显著，装填姿态对炮口点振动有一定的影响；装填姿态对章动角影响最大，质量偏心影响次之，质量偏心方位影响最小。