基于多传感器与多维空间的故障分类方法

何 永，文成林

（杭州电子科技大学 自动化学院，杭州310018）

从旋转机械系统中采集到最常见的是一维振动信号，通常采用小波变换和神经网络等方法进行时域频域分析。小波变换只是对信号的低频部分进行处理，这对于频域分析来说是不均衡的。BP 神经网络存在着学习速度慢且易陷入局部极小值等不足。

对于多维信号，常用多元统计方法对其进行分析。在多维信号每一维向量中，每个分量在时间上是常相关的，但对于同一时刻，由于各分量之间对应不同的物理量，相关性有强有弱，具有不确定性，多数表现为弱相关。振动信号采样存在固有的周期性， 因此适合利用多变量统计方法来处理这类信号。同一个周期内每一个采样点对应着对象相对位置的物理特性，因此同一个周期内的每个采样点仅与相邻的少数几个采样点有较强的相关性，而与距离较远的采样点相关性会逐渐减弱。而不同周期内的相同采样点之间因对应着同一物理位置的采样，其在时间上具有长时间相关性。因此，若把单个周期改为多维变量， 进而用多变量统计分析的方法，将会取得更好的故障诊断结果[1-4]。故在此建立一种基于多维空间时域特征值向量的故障分类方法。

1 算法描述

1.1 方法概述

在此所提出的基于时域振动信号在多维空间中的故障分类方法，一方面能够利用一维信号的周期特性，借助于成熟的基于多元统计分析的故障诊断方法。另一方面还可以将不同传感器采集的数据的特征进行组合得到多维向量，利用数学中的多维空间进行处理。多维向量在对应的多维空间中代表一个点，此处定义多维向量所在的多维空间为特征空间。

首先，将不同传感器采集的振动信号按照旋转机械的周期改写为矩阵形式，并求出该矩阵协方差阵的特征值，再将通过不同传感器计算的特征值组合，得到整个原始数据的特征值向量。其次，利用多维空间中不同向量代表不同的点也即代表不同的数据，对点进行划分以识别点对应的数据是属于哪一类故障。

1.2 信号预处理

对于一类源于旋转机械系统的振动信号序列组，如柴油机和轴承系统等

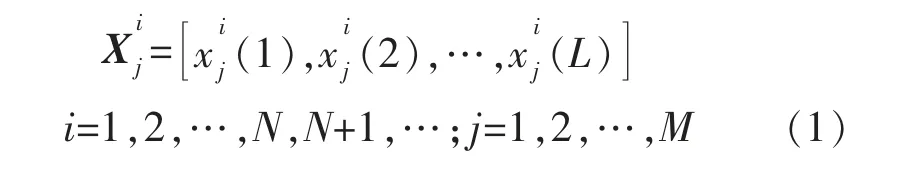
将旋转机械在第j 个传感器一个周期内的采样信号表示为向量，如其中r 为一个周期内的采样点个数。则多个周期内采样信号的矩阵形式为

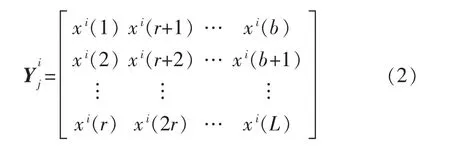
其中

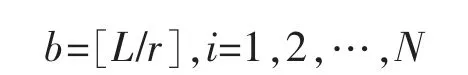
通常情况下，总的样本点数L 为r 的整数倍，否则可以对其进行截断或者补位处理。

令

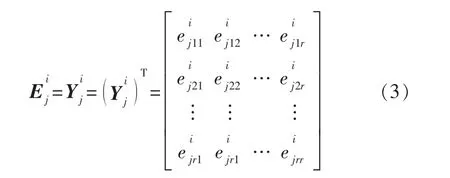
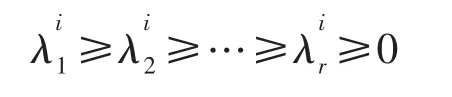
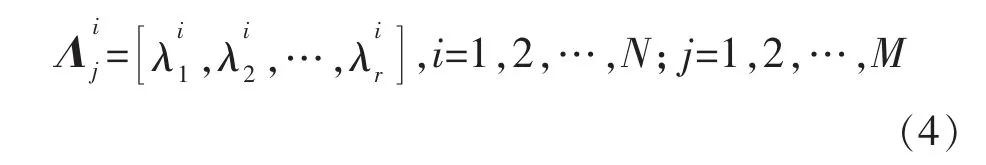
则将多个传感器采样得到的原始数据特征值记为

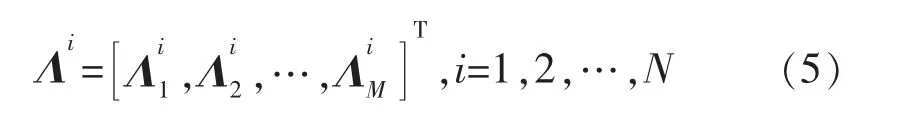
1.3 故障特征范围的确定

记特征值矩阵为D，即

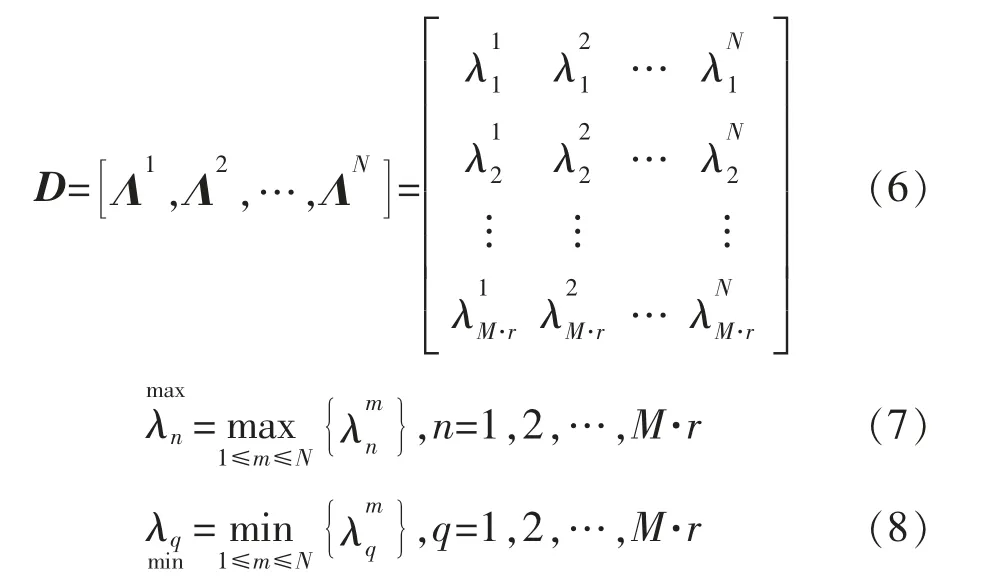
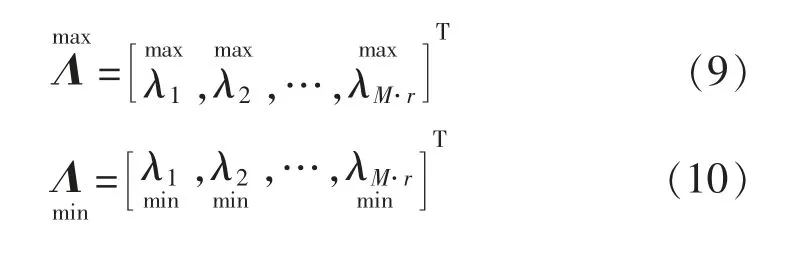
1.4 多维空间中的算法描述

在经典的三维空间中，2 个立体范围有无重叠，可以通过2 个立体边界有无重叠进行判断。比如，在三维空间中有2 个立方体，可以确定这2 个立方体各个顶点的坐标，并按纬度确定不同维度上的最大值和最小值，分别得到2 个立方体的2 个向量也即空间里的2 个点，此时立方体必然包含在对应的2 个空间点组合得到的空间里面。因此，就可以通过2 个空间点组合得到的空间来近似地表示该立方体，进而再确定2 个立方体是否重叠。如果是在多维空间，也可以通过类似的方法进行判断。具体的算法如下：

上述已经求得故障特征向量所在特征空间，并且对于训练数据来说，已经求得了特征空间中的范围。在此必需认识到，特征值向量上界和下界只是取前组数据对应特征向量同维度下的最大值和最小值，因为同纬度下的最大值和最小值已经具有一定的冗余，不必再进行加权。当有新的故障数据时，计算新数据的特征向量记为

将Λ 与各个训练数据计算得到的特征值向量上界和下界进行比较，判断Λ 代表的点属于哪一类故障。记

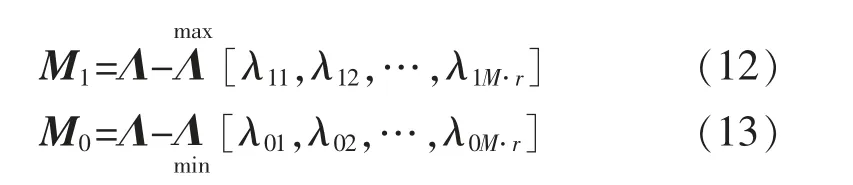
对M1和M0的不同纬度值进行以下处理：

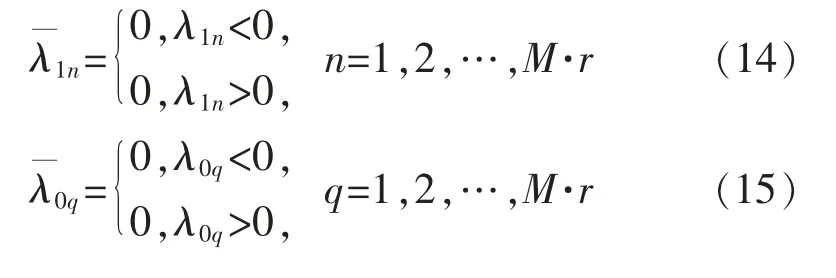
记

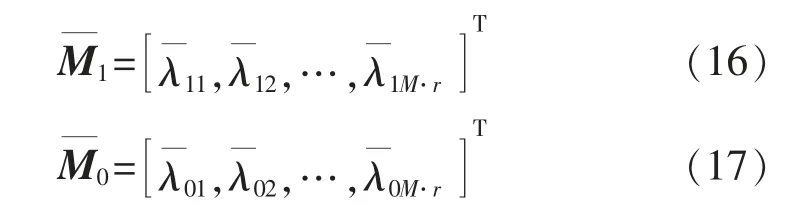
为尽可能减少误报，在此考虑用故障类型范围外的确定纬度所占总纬度的比例，而在数据处理初期就已经确定了特征空间，也即确定了总的纬度数，所以只需要计算故障类型范围外的确定纬度数。新数据的特征值向量与训练得到的所有类型故障的特征值向量的上下界进行比较，计算确定纬度数。最终找出确定纬度数最小的那一类，即测试数据属于该类故障。

2 仿真试验

试验在ZHS-2 型多功能电机柔性转子试验台上进行，试验台如图1所示。使用8 个安装在转子支撑座的水平和垂直方向传感器采集转子时域振动信号，经HG8902 采集箱将信号传输至上位机。

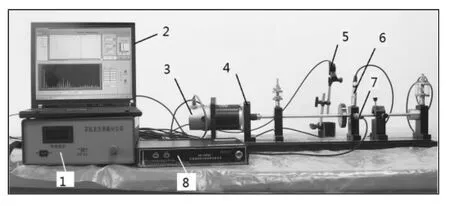
图1 ZHS-2 试验台Fig.1 ZHS-2 experiment platform

在试验台上模拟5 类情形：2 组转子不平衡，分别模拟发动机安装轴心存在偏差 （bph1，bph2）；基座松动 （jzsd） 用以模拟发动机固定出现松旷的现象；风机断叶（fjdy）模拟发动机内部散热部分故障；还有正常（zc）情况。

在该电机转子系统中，因故障引发的异常振动均可以通过传感器采集的振动信号反映出来，但其振动幅值与正常情况下相比， 会发生一定的变化。电机转子转速为1500 r/min，传感器的系统误差根据其生产厂商提供的精度设定为±1%。在每一类模拟的状态下， 每8 s 采集1 次， 连续采集300 组样本， 每组样本包含8 个传感器大约每隔0.0008 s 测得的10240 组数据。

对5 类模式分别采集300 组样本， 共1500 组样本， 每组样本又包含8 个传感器在8 s 内采集的10240 个数据。

MatLab 仿真流程如下：

步骤1对采集到的5 类模拟状态的信号进行改写。由于每一组数据都包含8 个采样器采集到的信号，所以将每一个传感器采集到的信号都改写为矩阵形式，并求其协方差矩阵的特征值。之后，将这8 个采样器信号得到的特征值进行组合， 得到该组数据的特征值。其余的数据也都经过上述过程的处理。由此，可以得到5 类模拟状态信号的特征值信息共1500 组，每一类特征值信息300 组。

步骤2在多维空间中求每类故障信号的范围。从1500 组数据中，取出1200 组即每一类取出240 组数据作为训练集；剩余的数据作为测试集，对该算法进行检验。

在ZHS-2 型多功能电机柔性转子试验台的参数设置中，电极转速1500 r/min，传感器的采样频率为1250 Hz。在此，将每一类故障中每组数据的每一维按照8 个一列进行改写，求其协方差矩阵的特征值得到8×1 的列向量；对剩余数据进行改写并求得特征值，将这些特征值组合就得到64×1 的特征值向量。

采用训练数据集，求得每类故障的特征值向量上界、下界，具体如下：（在此仅列出zc 数据组的特征值向量的上界和下界）

——zc 下界

［0.100154267 0.134582489 0.166101508 0.177042959 0.228974162 0.384610576 1.116704969 1.319367845 0.00318868 0.004038795 0.007728744 0.020103555 0.041809797 0.109435261 0.54029 0.835868629 0.017141043 0.01978346 0.049357662 0.062530949 0.100212005 0.131221285 0.146126738 0.156507026 0.153723893 0.294725829 0.403403747 0.436137097 0.474712989 0.590664575 0.974235777 1.07381792 0.195547269 0.226667017 0.282622982 0.324774592 0.355757965 0.387167798 0.457753782 0.499536213 0.040886284 0.05371101 0.093297683 0.107692576 0.181744494 0.381511166 1.250583917 1.430294285 0.047673472 0.049508868 0.055514249 0.058357037 0.078694955 0.110201999 0.192621773 0.219105292 0.188939802 0.210286684 0.227462086 0.252252902 0.29915077 0.318562574 0.412347111 0.459199602］

——zc 上界

［0.143413726 0.186103212 0.246980944 0.26012841 0.322606346 0.485243975 1.616306057 1.76071132 0.005461577 0.006311695 0.01080902 0.026212013 0.063021279 0.151904669 0.78067465 1.060943405 0.031386872 0.036323337 0.075249216 0.081445697 0.138489132 0.173517795 0.219050625 0.229191164 0.242194784 0.377493858 0.535144882 0.561925464 0.755551398 0.873865535 2.079954023 2.460502343 0.259552593 0.283669439 0.416612664 0.441123654 0.518314572 0.630062593 0.799752266 0.847673147 0.076274089 0.090765358 0.127444601 0.169640085 0.256782017 0.531581301 1.64080054 1.771292796 0.06857132 0.072658588 0.102733276 0.110148081 0.117376754 0.155194337 0.247138493 0.293334353 0.247402307 0.274133138 0.318106126 0.382089258 0.514013708 0.548489507 0.608847299 0.689615508］

将测试数据的特征值与训练数据得到的特征值的上下界进行比较， 并按照算法确定出纬度数，得到300 组测试 （每一类模式60 组测试数据），其结果见表1。

表1 试验结果统计Tab.1 Experimental result statistics

由表可知，在所有300 组测试数据中，误报率为1.33%，正确识别率为98.67%，能够较好地识别各类故障。

3 结语

所提出的基于多传感器采集数据在多维空间中的故障分类算法，仿真结果表明该算法能够较好地识别分类故障。然而，该方法尚有不足之处，该算法中通过最小确定纬度数进行分类，但是每一个纬度对于每一组数据属于哪一类故障的重要性，有待进一步研究。