热定型过程弹力针织物热塑性应变模型研究

周丽春，刘顺菁，金福江，楚贝贝

(华侨大学 机电及自动化学院，福建 厦门，361021)

幅宽与面密度是弹力针织物热定型加工过程中的2个重要质量指标。建立幅宽、面密度与热定型过程中的工艺参数的模型包括时间、温度、拉幅量和超喂量等是弹力针织物热定型研究的重点[1]，为精确设计热定型工艺参数提供依据，该模型是热定型过程的关键模型，在预测产品质量和设计工艺参数方面发挥着重要作用。目前国内外对于热定型生产过程的模型研究大部分是以实验和生产数据为基础的拟合模型。齐鲁等[2-3]利用动态黏弹谱仪通过改变温度来研究织物经向和纬向的动力学性能，在此基础上对温度与弹性针织物中纤维的松弛模量进行建模；钟丽莹等[4]以实验为依据阐释了织物经纬向伸缩率、热定型加热时间、温度与生产效率之间的关系，建立了可以预测面密度与幅宽的模型；郜琳琳[5]以误差最小为原则，选取多个优化目标，建立热定型温度、时间等工艺参数与织物幅宽、面密度间的模型；赵迪[6]根据前人的研究，为了提高质量指标面密度、幅宽预测模型的准确性采取了改进工艺参数与输出变量方案的方法，取得良好效果。但是，这些模型是在小样实验数据的基础上建立的，在实验数据的采样区间发生变化或数据有误差的条件下，模型对实际生产的作用会大大降低，因此这种模型局限性较大且缺乏普遍性。对于弹力针织物在热定型过程应变的理论模型研究，生产产品的热塑性在热定型工序中会受到影响，本文作者通过对热塑性的机理分析建立弹力针织物在热定型过程中的幅宽与面密度机理模型，并运用实际生产中的实验数据验证该模型的准确性与有效性。

1 热定型弹力织物经向和纬向变化分析

热处理过程是利用弹性纤维的热塑性，将织物加热到一定温度，消除其内应力，同时施加恒定张力将织物幅宽缓慢拉伸至生产指定规格后撤除外力并迅速冷却降温至织物的外形与尺寸处于平稳状态而不再发生改变。热定型织物经历了常温及升温拉伸和冷却收缩3个过程，其经向和纬向发生变化。

1.1 纬向变化量

上机后针织物首先固定布边在室温下进行拉伸，调整拉幅装置而产生恒力作用于织物，对织物起到纬向拉伸的作用。其次，升温过程是通过将织物放入烘箱，对烘箱设置温度，当烘箱的温度不断升高时，织物的应力会随之降低，由于织物受到张力，其纬向将被拉伸。最后，冷却过程即织物从烘箱取出后快速降温，该过程引起织物收缩。织物的纬向在这3个过程中都会发生一定的变化，其状态如图1(a)表示。由图1(a)可知：针织物纬向发生改变过程中存在4个状态，包括上机幅宽Wi、定前幅宽和定后幅宽以及下机幅宽Wo。状态间的变量包括由拉幅装置引起的拉伸形变量ΔW'、在烘箱中升温时产生的热塑性形变量ΔW+和冷却时的收缩变化量 ΔW-。故纬向变化量ΔW为

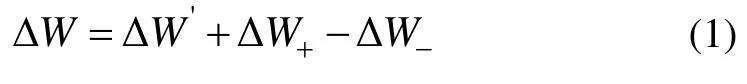
式中：ΔW为纬向变化量，cm；'ΔW为室温下由拉幅装置引起的拉伸形变量，cm。下机幅宽Wo为

1.2 经向变化量

经向变化过程与纬向变化过程类似，其区别在于纬向伸长的初始物理作用是通过拉幅装置提供而经向变化是由超喂装置实现。具体表现为超喂装置通过对喂布量进行控制从而在经向产生恒定张力。织物的经向伸缩变化在整个过程中的情况如图1(b)所示。故经向变化量ΔL为

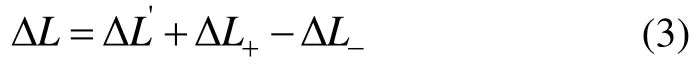
式中：ΔL为经向变化量，cm；'ΔL为室温下由超喂装置引起的拉伸形变量，cm；ΔL+为升温产生的热塑性经向形变量，cm；ΔL-为冷却时经向收缩形变量，cm。下机布长Lo为

式中：Li为织物的上机布长，cm。

综上所述，经向在热定型中的变化与纬向近似，其变化趋势相同，因此，为了简化计算，只需要选择经向或者纬向一种变化建立伸缩率模型即可，以经向变化量 ΔL为例进行研究。弹力针织物是由大量弹性纤维构成的，为了使问题简单化，假设忽略纤维与纤维之间的作用力，则可以对单根纤维的伸缩率建立模型。

据上述分析可知机械拉伸量(常温)Δ'L、热塑性形变(升温)ΔL+和收缩形变(冷却)ΔL-这 3 个因素是弹性纤维在热定型工序必不可少的部分。因此，弹性纤维伸缩率模型可以分解为3部分进行探讨，以下重点研究热塑性形变与收缩形变。

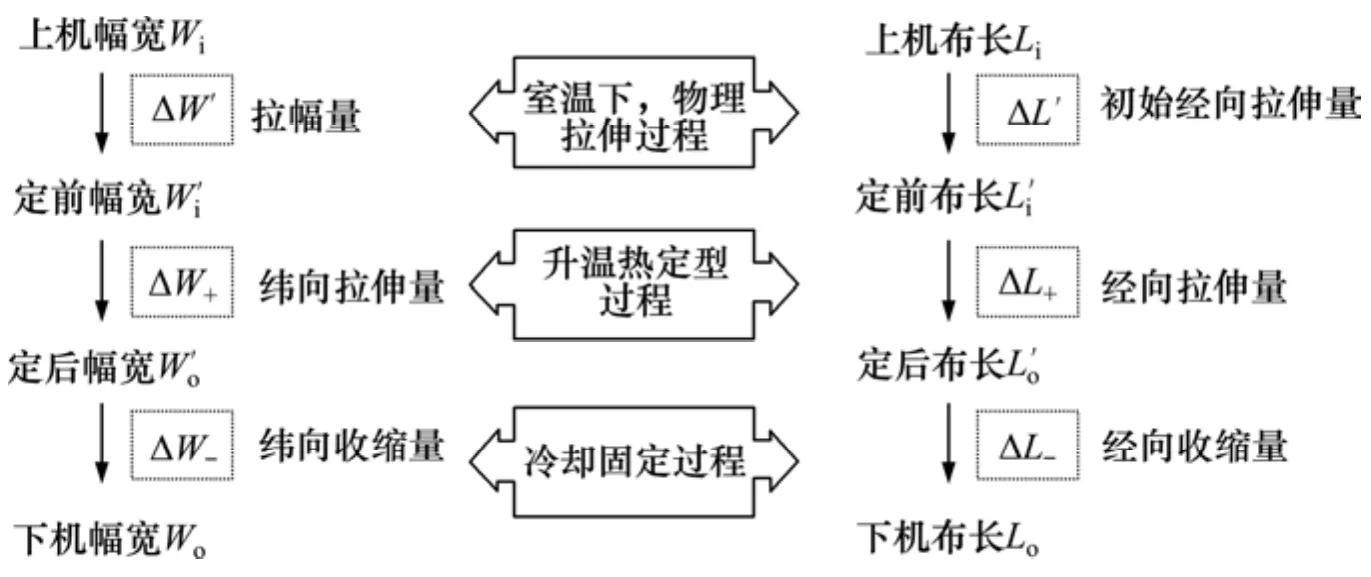
图1 形变量变化过程Fig.1 Shape variable change processes

2 弹性纤维热塑性形变模型

2.1 常温拉伸受力分析

1)应变与应力。应变定义为在有外力作用于物体却没有产生位移时，此外力使物体表现为局部形变。应力是物体单位截面的反作用力，它是在物体发生相对变形的情况下为了抵消外力作用而产生的[7]。应力为矢量，可分解为法线方向和切线方向2部分，分别以正应力σ和剪应力τ来表示。

2)应力与张力。弹性纤维在热定型过程中张力的方向与横截面相垂直，大小保持不变，纤维单位横截面积的拉伸正应力σ为

式中：σ为拉伸正应力，N/cm2；A为张力为F时纤维的横截面积，cm2。

3)应力与形变。纤维受到力的作用在拉伸过程中，根据V=AI⋅LI=AII⋅LII(其中，A表示横截面积，L表示纤维长度)。假定纤维体积V保持不变，横截面积和长度发生改变，即面积AI变化成AII，长度LI变化成LII时，截面积与拉伸长度成反比。根据Fl=σI⋅AI=σII⋅AII可知当应力σ由σI变化成σII时，截面积与应力成反比。综上分析，应力与拉伸长度成正比，关系可以表示为

在应力表达式(5)中，当A表示热定型过程中受到张力作用下的实时横截面积，此时应力σ被称作真实应力。当Ai表示弹性纤维的初始截面积时，应力σa则被称为许用应力[8]。

由式(6)可得

式中：L为瞬时布长，cm；σa为许用应力，N/cm2。故有

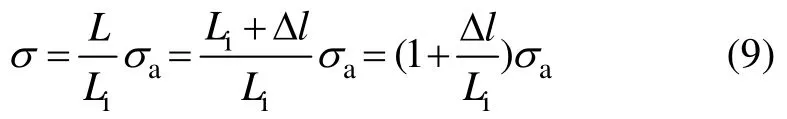
式中：Δl为实时布长变化值，cm。

4)应变与形变。假设纤维的应变不大，那么由式(10)来描述拉伸应变即拉伸后纤维的变化量与初始长度的比值[9]。

式中：ε为工程应变。

5)高弹应变。其特点是弹性模量Eg小，应变大且随时间发生变化，应变相对滞后于应力[9]。高弹应变发生的的条件是常温下实际应力足够大或正常拉伸状态时的温度高于玻璃化温度。

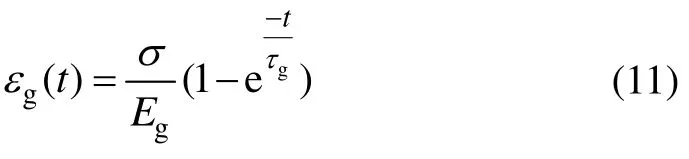
式中：τg为高弹形变松弛时间，s。

6)塑性应变。塑性应变的特点是应力较小的状态下产生的应变巨大，而且应变量在外力消失后无法复原[9]。塑性应变产生的条件是常温下实际应力较大且足以克服屈服应力或者正常拉伸时的温度高于黏流温度。

式中：ηs为黏度，Pa·s。

2.2 定张力加热应变模型

1)定张力加热应变。定张力热定型过程中在纤维伸长这个宏观的状态下发生新的高弹形变。因此，其应变表达式为

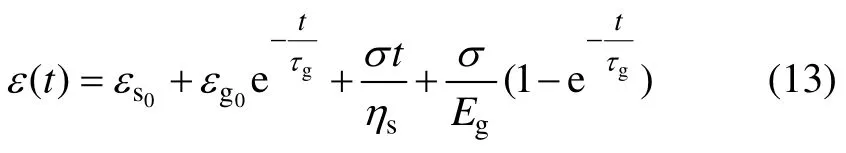
式中：Eg为实时高弹模量；εs0为原塑性应变；εg0为原高弹应变；为松弛回复后剩余的高弹应变；σt/ηs为在应力σ作用下新塑性应变；为在σ作用下新高弹应变[10]。

2)恒拉力F作用下的原应变量。弹力织物在常温下其拉伸瞬间状态满足胡克定律，拉力F可由式(7)和(10)计算。在t0时间内织物被持续拉伸，当其大于拉伸负荷时，将产生原高弹应变：

式中：εg0为恒拉力下提供的原应变量；Eg0为初始弹性模量；σ0为原高弹应力，N/cm2；t0为持续拉伸时长，s；τg0为初始松弛时间，s。

原塑性应变为

式中：εs0为原塑性应变量；σ0为原高弹应力，N/cm2；ηs0为初始黏度，Pa·s。

3)加热应变高弹形变松弛时间、弹性模量及黏度。式(13)中，应变ε和应力σ的计算公式已推导，见式(8)和(9)。下面计算其余3个量即松弛时间τg、高弹态下的弹性模量Eg以及黏度ηs。

① 高弹形变松弛时间τg。τg的一般公式为[10]

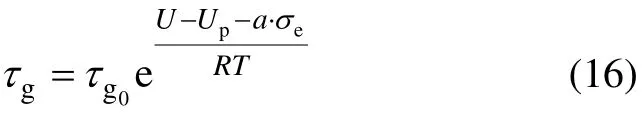
式中：U为摩尔高弹活化能，J；Up为因增塑而导致高弹活化能的降低，J；a·σe为应力所导致高弹活化能的降低，J；R为气体常数，R=8.307 6 J/(mol·K)；T为热力学温度，K。

令Ea=U-Up-a⋅σe为系统下降的总活化能，则式(16)变为

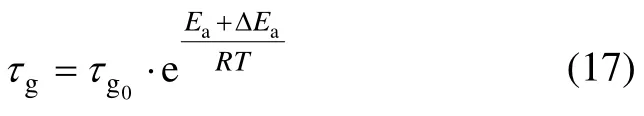
当温度波动较小时，Ea可视为常数，一般对于固体高聚物有Ra=1.6×102J/mol[10]。

热定型过程中由于织物受到张力作用，纤维分子的运动受到限制，因此，需要克服能量增加。故此过程中的松弛时间τg为

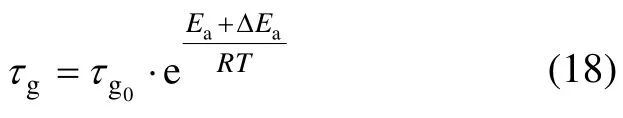
式中：ΔEa为松弛阶段需增加的能量，J。

将初始温度T0与总活化能Ea的数值代入式(18)中，可求得 ΔEa≈ 0.1RT0-Ea= 83.41 J/mol。因此，将理想气体常数R，总活化能Ea及增加的活化能ΔEa数值代入式(18)中可得紧张热定型过程τg的表达式为

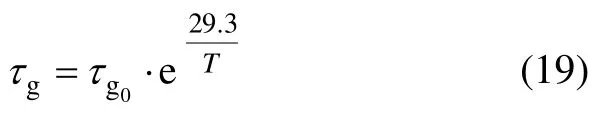
② 弹性模量。高弹形变是指在高弹状态下物质发生的形变，当弹性针织物由普弹态变为高弹态时，其弹性模量受温度影响，存在松弛现象，因此，也发生相应的转变。引入弹性模量E，在室温T0时，

通过单位体积内网链构象熵的改变计算应力σ有[11]

当式(22)中温度T为室温T0时，与式(20)相等，故可求得

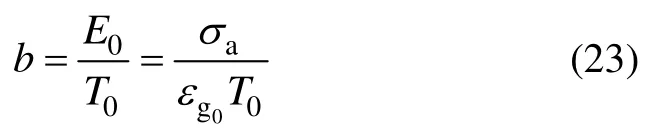
温度保持不变的条件下拉伸弹性纤维，并维持其应变ε=εg0不变，应力松弛现象可以表示成线性黏弹性的Maxwell模型[11]。该模型由1个弹簧和1个液体黏壶组成的，其表达式为

式中：τm为应力松弛时间，τm=η/E，s；η为液体黏度，Pa·s；E为弹簧弹性模量；σ0为模型受力形变时的初始应力，这里初始应力为σa，N/cm2；σ(t)为t时刻模型的内应力，N/cm2。时间为t时弹性纤维的弹性模量E(t)为

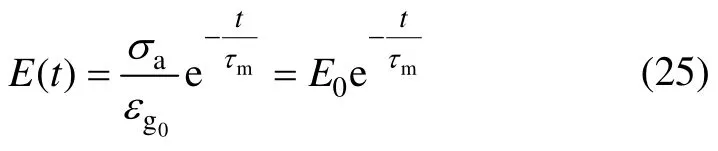
式中：E(t)为应力松弛模量；E0为起始弹性模量；τm为应力松弛时间。

由于纤维满足时温等效理论[12]，结合式(22)和(25)可得高弹模量的最终表达式为

式中：系数c=ηg/b；ηg为弹性纤维高弹态下的黏度，Pa·s；b为弹性纤维的温模系数。

③黏度ηs。在高弹态条件下纤维由玻璃态转变成黏流态其黏弹性保持恒定，可视为常数[13]。计算高弹黏度ηg和黏流黏度ηs可研究黏流态。此状态的黏度与时间的关系具有以下形式：

式中：Eη为流动活化能，J。当T在一定范围内时，ηs与T成反比。

弹性纤维处于黏流态条件下，其分子网络相互交联时的黏度ηs为常数可以表示成ηs=ηs(Ttrans_s)，其中Ttrans_s为分子从高弹态过度到黏流态的温度。且此状态的黏度ηs与高弹态黏度ηg相等[14]。

因此，可以分析高弹态黏度ηg在平稳状态下的求解。已知黏流态下弹性纤维的黏度ηs(T)为 103～104Pa·s[13]，由于转折温度Ttrans_s取温度范围内的最小值，根据黏度与温度成反比的关系故其黏度应取范围的最大值，有

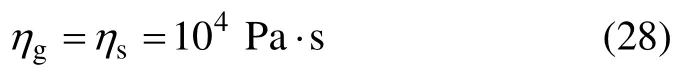
2.3 加热形变模型综合

弹性织物初始应变量的累积是从上机后到室温下的拉伸直到热定型前的拉伸过程，此过程中的布长由Li拉伸到，初始拉伸量为。

在拉伸过程中织物的高弹应变量较小，有

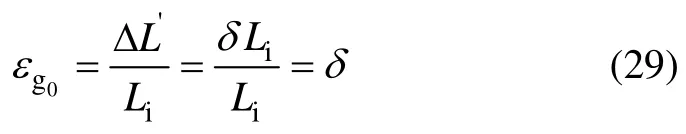
由式(7)可以计算出许用应力σa，由式(9)可求出原高弹应力σ0为

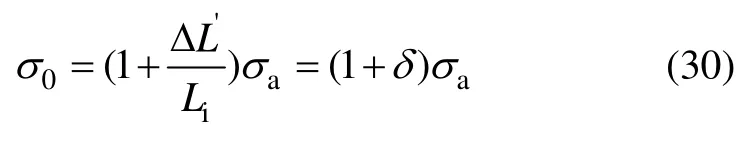
令从布匹上机后到布匹置入烘箱前的距离为s0，若车速v1保持不变，则拉伸时间t0为

由式(20)和(29)可求得弹性纤维正常状态下的弹性模量，结合式(31)可得弹性纤维的初始高弹模量Eg0为

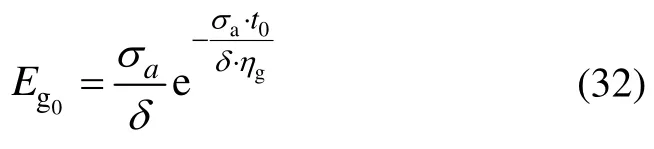
将式(30)～(32)代入式(21)可得初始高弹形变松弛时间τg0为

此时，在拉伸力Fl的作用下，实际应力小于屈服应力，因此，初始的塑性应变为零，即

综上所述，将式(14)，(15)，(18)，(19)，(26)，(27)，(33)和(34)代入(19)可推导出升温过程中的热塑性形变量公式：

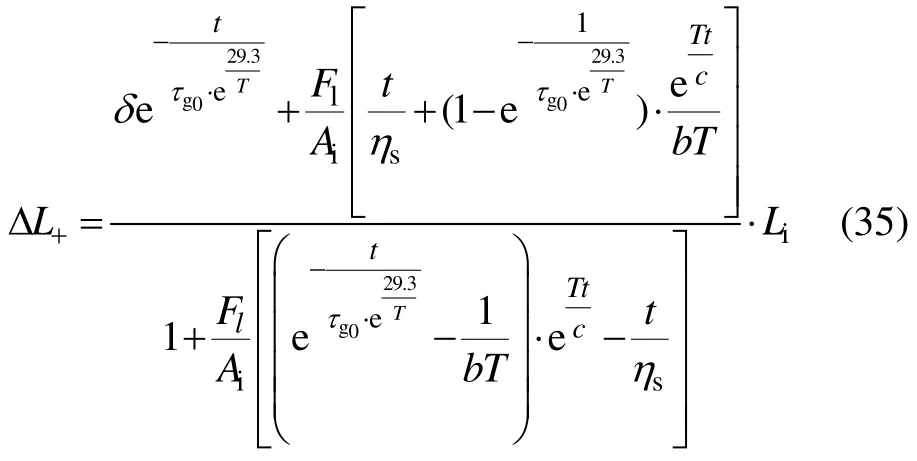
式中：t为纤维热塑性阶段定型时间，t=st/v1；st为热定型过程中烘箱的长度。

2.4 冷却收缩形变模型

假设冷却过程的温度为Tc(单位为 K)，使其保持恒定，故收缩过程温差 ΔT=T-Tc，T为定型温度。弹性纤维收缩率为C=ΔL-/Li。在松弛状态下，纤维的收缩率与定型温度和收缩时间有关，温度增高或者时间增长都会使收缩率变大，因此，纤维的收缩率如下式所示[15]：

式中：tc为冷却收缩时间，tc=sc/v1，s；sc为冷却过程中的部分热定型机的长度，m；K为玻尔兹曼常数；h为普朗克常数；ΔEs为冷却收缩活化能，与冷却温度有关。在冷却过程中，当温度设置为 70℃时，ΔEs=39.04 kJ/mol；当温度设置为 95℃时，ΔEs=14.9 kJ/mol[16]。

综上可知冷却收缩布长ΔL-为

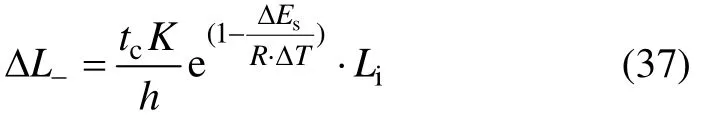
3 弹性纤维伸缩率模型

将式(9)，(35)和(37)代入式(3)可得弹性纤维伸缩率模型。

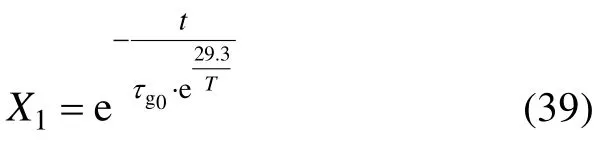
其中：

4 热定型幅宽和面密度模型

弹力针织物伸缩率模型体现为ΔWf=f1(T,VL,t,C)以及ΔGf=f2(T,VL,t,C)，其中，ΔW为门幅，ΔG为面密度。工艺参数包括温度T，拉幅量VL，时间t，超喂量C。忽略织物中各纤维之间的相互作用，织物的拉伸量可以用纤维的拉伸量来表示，其模型如下[17]。

4.1 幅宽模型

由织物的经向模型公式(38)可以推出纬向的伸缩率为

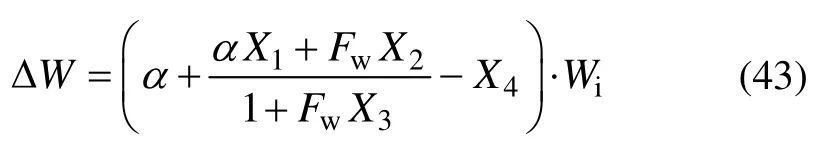
式中：X1，X2，X3和X4见式(39)～(42)。

由式(2)可得下机幅宽Wo为

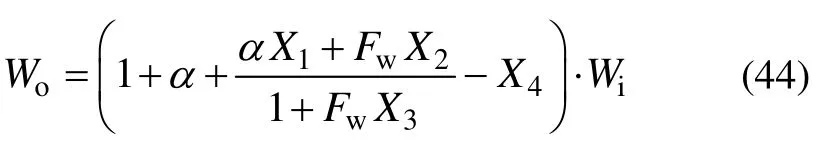
4.2 面密度模型

面密度模型中包含上机变量和下机变量，其中上机时的变量是可测的[18]，而下机变量可由公式求得。下机幅宽Wo由式(44)计算得到。

另外，由式(4)和(44)求得下机布长Lo为

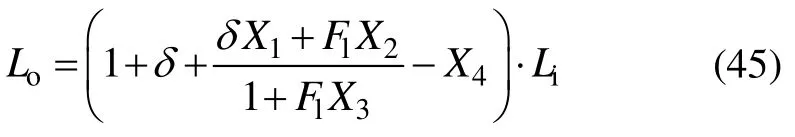
假设织物面密度分布均匀，且进、出布时织物总重量GA维持恒定，因此有GA=Gi⋅WiLi=Go⋅WoLo，故可求得面密度Go为

将式(43)和(44)代入式(45)得出下机面密度Go为

5 模型实验验证

以JC14.76T+2.22T的弹力针织物为实验对象，从数据表中随机抽取10组数据，分析真实值与计算值的误差来验证该伸缩率模型的准确性。生产数据表如表1所示。

5.1 幅宽伸缩率模型验证

测得纤维的拉伸弹性系数kw=0.417 7 cN/mm以及初始截面积Ai=1.931 tex。通过式(44)可计算出织物下机幅宽并与真实值对比，结果如表2所示。

由表2可知：幅宽计算值与真实值间相对误差最大值为 0.85%，处于允许误差范围内。求得模型中残差平方和数值较小为7.583，拟合优度R2为0.984，因此，计算值与真实值的拟合效果好且精确度高。

5.2 面密度伸缩率模型验证

测得纤维拉伸弹性系数kl=1.526 cN/mm，根据式(47)计算出织物的下机面密度，并与生产真实值进行对比，结果如表3所示。

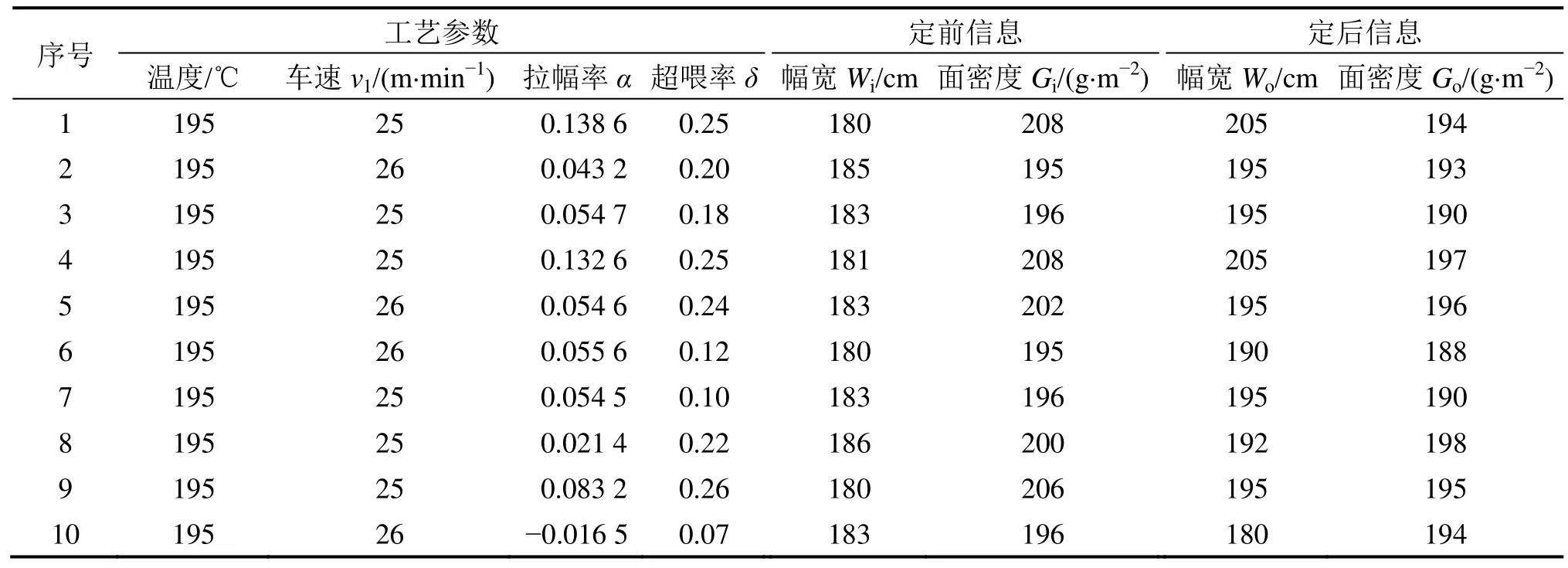
表1 生产数据表Table 1 Production data table

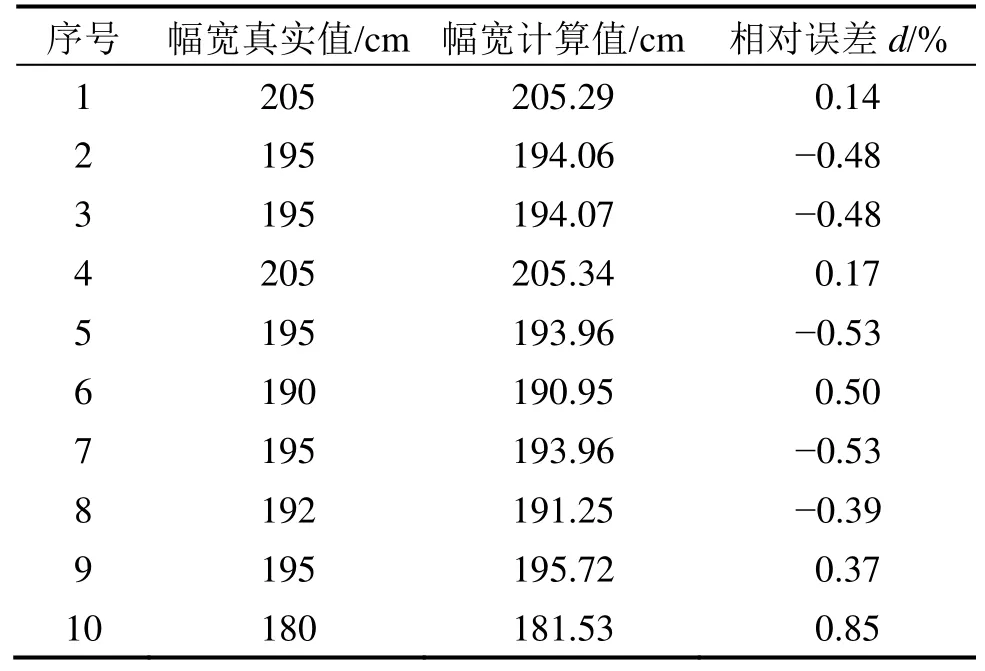
表2 织物幅宽伸缩率模型有效性验证Table 2 Validation of fabric width expansion ratio model

由表3可知：面密度计算值与真实值间的相对误差最大值为 0.89%，在允许误差范围内。求得模型中残差平方和数值较小为7.022，拟合优度R2为0.953，因此，计算值与真实值的拟合效果好且精确度高。

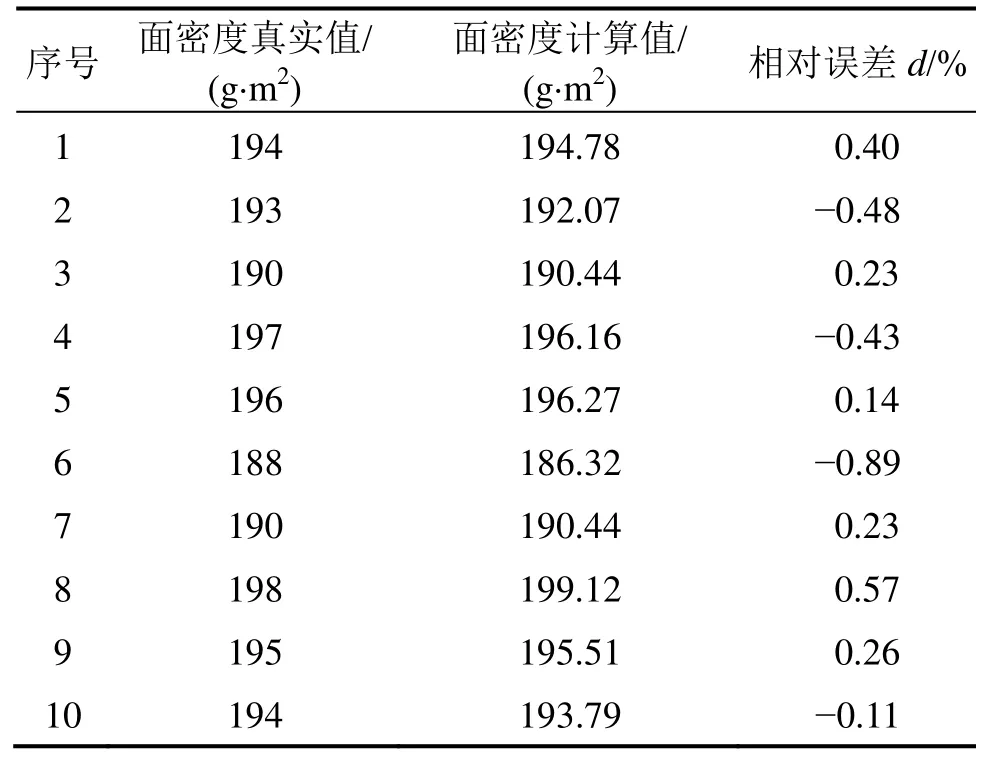
表3 织物面密度模型有效性验证Table 3 Validation of fabric gram weight expansion ratio model

6 结论

1)通过对热定型过程中弹力织物在常温拉伸、加热伸缩、冷却收缩这3个阶段经向和纬向受力分析，得到弹力织物经向和纬向综合应变模型，最终建立了烘箱温度、超喂、拉幅量等工艺参数与幅宽、面密度质量指标间的应变机理模型。

2)该机理模型的结构虽然复杂，但可以准确描述出热定型过程弹力织物面密度、幅宽与温度、车速、超喂和拉幅量的关系，并通过实际的热定型实验数据验证了该机理模型具有较高的准确性与有效性，为解决热定型工艺参数精确、定量设计提供了可靠的理论支持，对提高染整行业热定型生产技术水平具有重要作用。