轨道交通周期型声屏障带隙特性及其降噪性能

易强，王宇航，高鑫，赵才友，王平



轨道交通周期型声屏障带隙特性及其降噪性能

易强1, 2，王宇航1, 2，高鑫1, 2，赵才友1, 2，王平1, 2

(1. 西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都，610031；2. 西南交通大学 土木工程学院，四川 成都，610031)

基于声子晶体带隙理论提出气−固周期型声屏障，基于Bloch定理，采用传递矩阵法研究周期型声屏障声波带隙特性，同时建立有限元模型对带隙进行验证；分析固体材料密度、声速及填充率对周期型声屏障带隙的影响；输入实测轮轨噪声声源，分别研究直立式与全封闭周期型声屏障对轮轨噪声的控制效果。研究结果表明：气−固周期型声屏障中固体材料密度的增加可以显著降低带隙起始频率，同时使截止频率升高、带隙宽度增大；当固体材料填充率取为0.5时，带隙起始频率最低，而截止频率随填充率增大而升高；直立式周期型声屏障比同等质量单一材质声屏障的降噪效果提高2~3 dB，而引入带隙后的全封闭周期型声屏障降噪效果可提高3~5 dB。

轨道交通；声子晶体；声屏障；带隙；噪声控制

随着轨道交通的快速发展，列车运行引发的环境噪声问题愈发突出，并已成为沿线居民投诉的热点问题[1]。轨道交通噪声不仅会给人带来不适感，长期暴露于过大的噪声环境下，还会影响正常的生产和生活，因此，需要采取科学合理的降噪措施。在现有技术条件下，国内外研究人员大量采用声屏障来治理轨道交通沿线噪声污染问题[2]，但是，对于某些噪声敏感点，控制要求更加严格，因此，有必要开发降噪性能更加优越的声屏障结构。声子晶体定义为弹性常数或者密度周期分布的材料或结构，并具有重要的物理特性即弹性波带隙[3−4]。在带隙频率范围内弹性波无法自由传播，呈现明显的衰减特征。声子晶体带隙特性为噪声控制提供了全新的研究思路和方法，因此，可通过设计具有带隙特征的周期型声屏障，实现轨道交通环境噪声的进一步控制。人们基于声子晶体带隙理论，开展了大量的弹性波传播特性及控制研究。从带隙产生机理分类，目前主要有Bragg散射机理[5]和局域共振机理[6]。对于Bragg散射机理，带隙主要由周期变化材料与弹性波的相互耦合作用产生，而局域共振带隙主要取决于局域共振单元自身的谐振频率与基体中行波的相互作用。利用声子晶体Bragg带隙开展声学控制研究得到了广泛关注。PICHARD等[7]采用平面波展开法研究了二维周期排列方柱的声波带隙特征；KOUSSA等[8]通过在传统声屏障内侧附加声子晶体结构，发现附加声子晶体的声屏障可在中高频范围内有效控制道路交通噪声的传播。MORANDI等[9]建立周期性声屏障足尺模型(该结构由3层PVC管周期排列而成)，通过试验研究了周期性声屏障对声波的反射和透射特性，并在Bragg频率附近得到最大插入损失。此外，ELFORD[10]等利用竹、木、金属等材料作为散射体，同时附加吸声材料或空腔结构，形成新型周期性声屏障。但目前提出的周期型声屏障主要以二维声子晶体结构为主，其尺寸较大，难以应用于轨道交 通。另一方面，局域共振机理为低频弹性波控制提供可能。李硕[11]在均匀板上周期性嵌入局域共振结构实现了局域共振带隙频率范围内隔声性能的提升。张佳龙等[12]提出一种正八边形孔状局域共振型声子晶体结构，利用有限元方法分析了该结构的带隙机理和低频隔声特性。YUAN等[13]构造新型局域共振结构并使弹性基体与流体基体交替排列，利用多重散射理论分析了局域共振带隙与Bragg带隙的耦合效应并实现低频带隙的拓宽。但相对于Bragg带隙，局域共振带隙较窄且结构更加复杂。目前，基于声子晶体带隙理论的噪声控制研究已取得了重要进展[14]，但所涉及的结构尺寸较大或结构较复杂。VASSEUR等[15]研究了钨/铝和碳/环氧树脂声子晶体，发现相邻材料纵波波速与密度相差越大，越可能实现完全带隙。REINKE等[16]研究了弹性波在固/固型和气/固型周期结构中传播的带隙特性，认为阻抗匹配差异越大的材料组合更容易产生宽频带隙。因此，本文作者基于Bragg带隙机理提出气−固周期型声屏障结构，以期进一步控制轨道交通轮轨噪声的传播，为城市轨道交通环境噪声控制提供新的研究思路和方法。

1 理论模型

选取阻抗差异较大的材料构成周期结构可实现弹性波带隙频率范围的最大化，因此，本文采用固体和空气构成气−固周期型声屏障[17]，声阻抗分别为1=11和2=22(其中1和2为不同介质材料的密度；1和2为不同介质波速)，2种材料在声屏障厚度方向即方向上交替排列形成周期结构，在一个周期中2种材料的厚度分别为1和2，晶格常数=1+2，周期型声屏障示意图如图1所示。

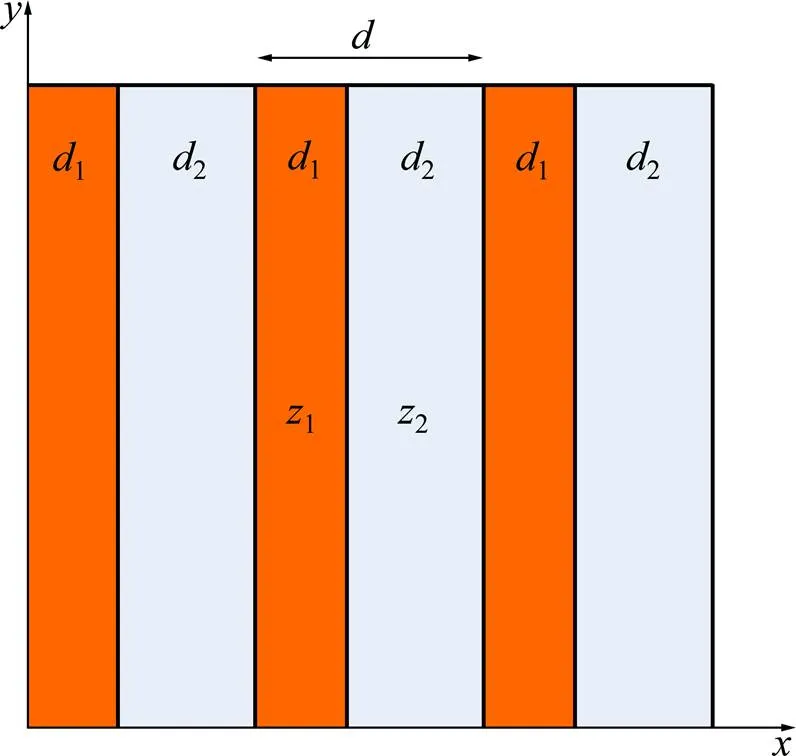
图1 周期型声屏障示意图

在一维周期结构声场中，声压p满足一维波动方程[18]：

式中：c为声波在介质中的波速，=1, 2;为时间。

式(1)的平面波解为

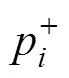
根据2种材料交界面处的声压连续性条件及法向速度连续条件可求得界面处的传递矩阵：

当声波经过厚度为d的介质时，声压1经传递矩阵作用变为2，介质中的传递矩阵为

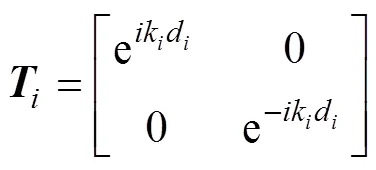
弹性波通过1个基本周期单元的传递矩阵为

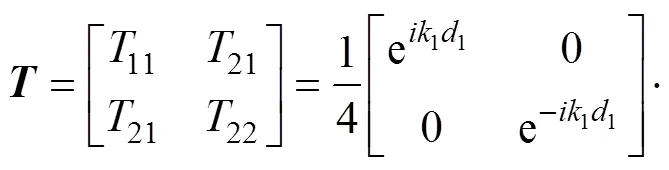
式中：1=2π/1；2=2π/2；为入射波频率。

根据Bloch定理，对于周期结构中的弹性波，其物理场与相邻周期相关[3]：

式中：为Bloch波数。结合传递矩阵，可得周期型声屏障结构弹性波传播特征方程为

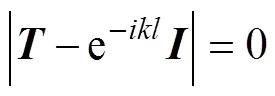
式中：为单位矩阵；Bloch波数实部表示弹性波相位改变，虚部表示弹性波的阻尼，即波的传播衰减系数。求解特征方程（8）可得波数与频率之间的关系，即频散特性。

011122(211122)−120(9)

01，20，12和21可由式(4)得出：1和2可由式(5)得到。

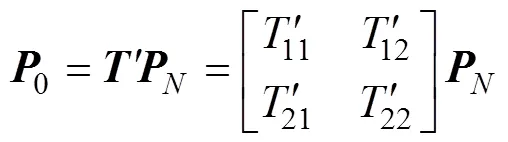
由此可得有限周期型声屏障的透射系数t和反射系数r为[19]：

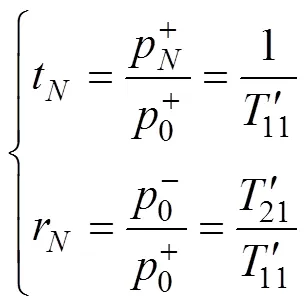
透射率T和反射率R为

透射率T和反射率R即可表征声波在气−固周期型声屏障中的传播特性。

2 计算结果及验证

以空气和聚碳酸酯材料组成的气−固周期型声屏障为例，设计3个周期的声屏障，晶格常数=60 mm。在一维周期结构的研究中，通常根据11=22的关系式‍[20](即1/1=2/2，声波在2种材料中通过的时间相同)确定合适的元胞厚度。本文分别取1个元胞中聚碳酸酯和空气的厚度分别为49.3和10.7 mm，材料参数如表1所示。

表1 材料参数

根据传递矩阵法计算得到周期型声屏障频散曲线，如图2所示。周期型声屏障第1阶带隙频率范围为123~ 15 670 Hz，在该频率范围内，声波将无法自由传播而呈现衰减特性。且此时带隙频率范围极宽，可用于抑制宽频范围内轮轨噪声的传播。为了分析声波在有限周期声屏障内的传播特性，采用式(12)计算3层气−固周期型声屏障透射率，并同时建立3层气−固周期型声屏障有限元模型，计算得到其声透射率曲线，如图3所示。由图3可知：在带隙频率范围内，声波传播存在明显的衰减，由此可验证理论计算的正确性。

图2 周期型声屏障频散曲线

1—理论计算结果；2—有限元结果。

3 带隙影响因素分析

气−固周期型声屏障由固体材料和空气交替排列组合而成，而固体材料选择范围广，因此，有必要分析固体材料填充率s、密度1和波速1这3个因素对带隙的影响规律，从而设计合理有效的轨道交通周期型声屏障。带隙影响因素及其水平见表2。

各因素对带隙频率的影响如图4所示。由于实际声屏障结构高度有限，因此，建立2 m高周期型声屏障有限元模型，分别采用传递矩阵法和有限元方法，计算得到其带隙频率范围(见图4)。

由图4可知：固体材料密度1对带隙起始频率的影响最显著，且随着密度增大，起始频率呈现逐渐降低的规律；固体材料填充率s对起始频率的影响较显著，随着s的增大，起始频率先减小再增大，在s=0.50左右时起始频率达到极小值；而固体材料声速1对起始频率的影响较弱。

表2 带隙影响因素及其水平

(a) 各因素对带隙起始频率的影响曲线；(b) 各因素对带隙截止频率的影响曲线

固体材料密度1对带隙截止频率的影响较显著，且随着密度1的增大，截止频率呈现先降后升的规律；超过一定水平后，固体材料密度1与固体材料声速1对截止频率的影响曲线相近；固体材料填充率s对截止频率的影响最为显著，随着s的增加，截止频率逐渐升高。

图5所示为在固体材料声速1和密度1不变，晶格常数分别为60，70和80 mm时，带隙频率随固体材料填充率s的变化。由图5可知：晶格常数减小能够同时提高带隙起始频率和截止频率，且对截止频率影响显著，使得带隙频率范围增大。在实际工程应用中，可以根据城市轨道交通噪声的频谱特性，设计带隙起始频率较低且带隙位置与噪声主频相符的周期型声屏障。

(a) 晶格常数；(b) 对截止频率的影响

4 周期型声屏障降噪效果研究

列车在运行过程中产生噪声主要包括轮轨噪声、结构二次噪声、空气动力噪声和电气设备噪声等[21]。其中，轮轨噪声作为主要声源向外界辐射噪声[22]，因此，可采用气−固周期型声屏障对其进一步控制。选取车速为100 km/h的城市轨道交通实测轮轨噪声作为噪声源，噪声频谱如图6所示。

图6 轮轨噪声声源频谱

4.1 直立式周期型声屏障降噪效果分析

为研究直立式气−固周期型声屏障对轮轨噪声的控制效果，建立直立式周期型声屏障模型，如图7所示。声屏障高为2 m，固体材料声速1为2 750 m/s，晶格常数为60 mm，填充率为0.5。以距桥梁中心线7.5 m，轨面高度位置为受声点，分析直立式周期型声屏障的降噪效果。当固体材料密度为1 000 kg/m3时，周期型声屏障弹性波带隙频率范围为130~5 600 Hz。在分别安装直立式单一材质声屏障和周期型声屏障情况下，受声点处噪声频谱如图8所示，其中单一材质厚度为90 mm。尽管部分轮轨噪声以绕射方式进行传播，但相对于同等质量的直立式普通声屏障，气−固周期型声屏障可进一步降低轮轨噪声2~3 dB。直立式周期型声屏障附加插入损失如图9所示。由图9可知：在带隙频率范围内周期型声屏障附加插入损失最大可达约12 dB，而在带隙边界处，周期型声屏障附加插入损失明显降低，此时，声波可通过声屏障进行传播。

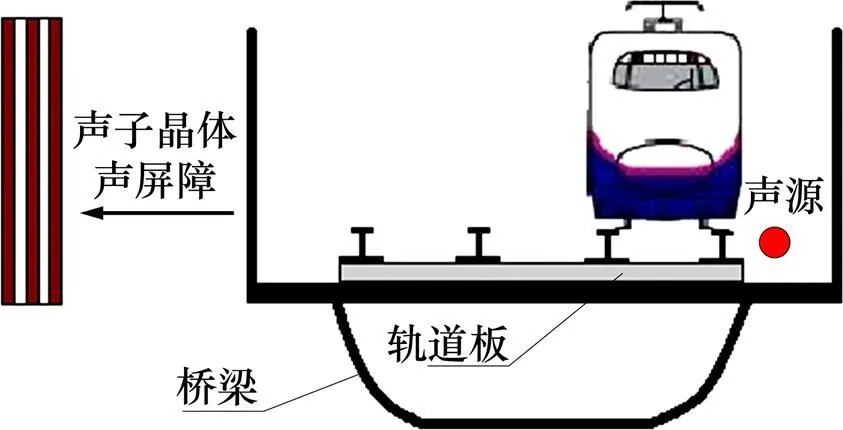
图7 直立式周期型声屏障模型示意图

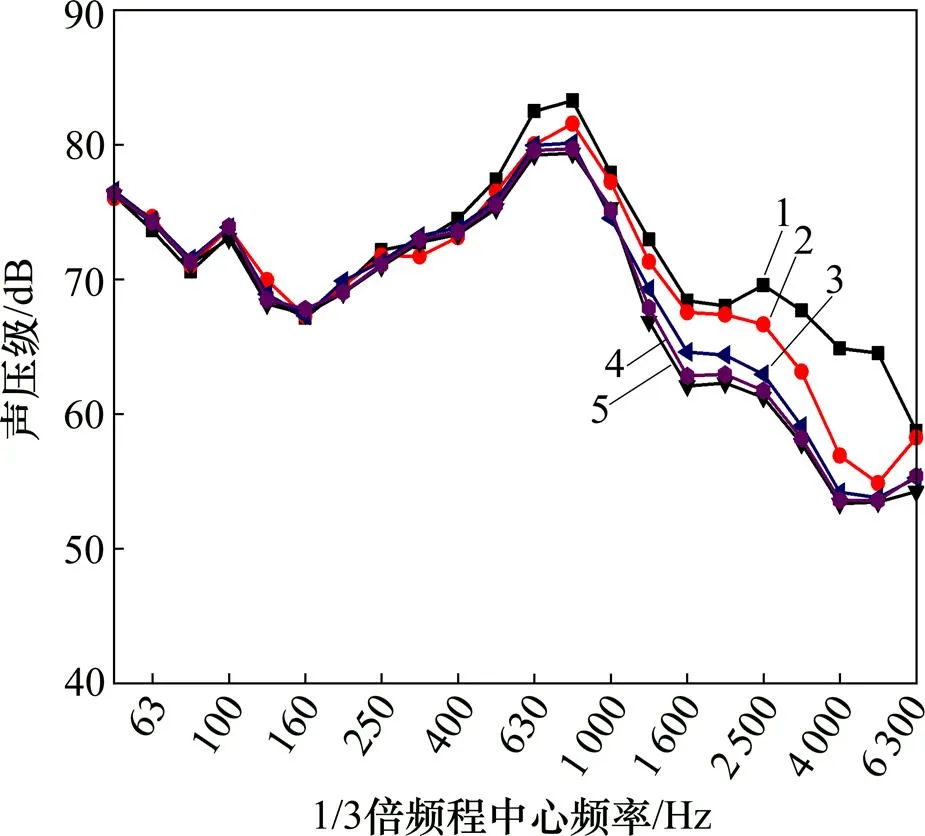
材料密度/(t∙m−3)：1—1(单一材质)；2—1(周期型)；3—3(周期型)；4—5(周期型)；5—7(周期型)。

材料密度/(t∙m−3)：1—1；2—3；3—5；4—7。

4.2 全封闭式周期型声屏障降噪效果分析

下面分析全封闭式周期型声屏障对轮轨噪声的控制效果，此时，轮轨噪声均以透射的方式向外界传 播[23]。图10和图11所示分别为全封闭周期型屏障受声点噪声频谱及其对轮轨噪声的控制效果。由图10和图11可知：相对于单一材料声屏障，周期型声屏障在带隙频率范围内能够进一步降低轮轨噪声的传播，降噪效果可提升3~5 dB。即使在相同厚度(150 mm)条件下，周期型声屏障的降噪效果亦优于单一材质的声屏障的降噪效果。

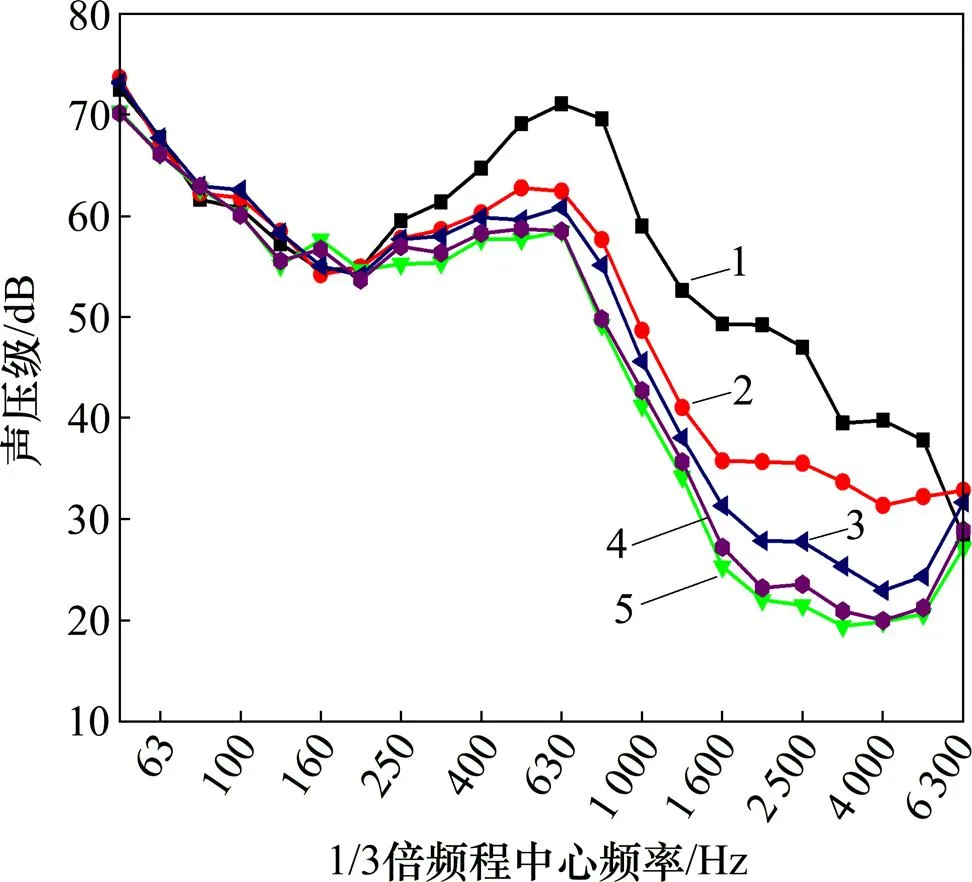
材料密度/(t∙m−3)：1—1(单一材质)；2—1(周期型)；3—3(周期型)；4—5(周期型)；5—7(周期型)。

1—声源；2—单一材质，厚度为90 mm；3—单一材质，厚度为150 mm；4—周期型声屏障。

5 结论

1) 固体材料密度及填充率对带隙起始频率的影响显著，密度的增加可以显著降低带隙的起始频率，当填充率为0.5时，带隙起始频率最低；而固体材料声速对于起始频率的影响则不明显。带隙截止频率受固体材料填充率的影响最显著，填充率的增加使得截止频率提高且带宽增大。带隙的起始和截止频率均随着晶格常数的增大而降低，通过增大晶格常数可以得到低频带隙。

2) 全封闭式周期型声屏障比同等质量的单一材质声屏障的降噪效果更佳，可以提高3~5 dB；由于部分轮轨噪声绕射，直立式周期型声屏障比同等质量的单一材质声屏障的降噪效果稍好，可以提高2~3 dB。

3) 由于固体材料与空气阻抗差异大，因此气−固周期型声屏障选材范围广，在进一步提高声屏障降噪效果的同时实现声屏障的轻质化。

[1] 易强, 王平, 赵才友, 等. 高架铁路环境噪声空间分布特性及控制措施效果研究[J]. 铁道学报, 2017, 39(3): 120−127.YI Qiang, WANG Ping, ZHAO Caiyou, et al. Spatial distribution characteristics and reduction measures of the environmental noise in elevated railway region[J]. Journal of the China Railway Society, 2017, 39(3): 120−127.

[2] 周信, 肖新标, 何宾, 等. 高速铁路声屏障插入损失影响因素及规律[J]. 西南交通大学学报, 2014, 49(6): 1024−1031. ZHOU Xin, XIAO Xinbiao, He Bin, et al. Influential factors and rules insertion loss of high-speed railway noise barriers[J]. Journal of Southwest Jiaotong University, 2014, 49(6): 1024− 1031.

[3] 温熙森. 人工周期结构中弹性波的传播: 振动与声学特征[M]. 北京: 科学出版社, 2015: 15−20. WEN Xisen. Propagation of elastic waves in artificial periodic structures: vibration and acoustic characteristics[M]. Beijing: Science Press, 2015: 15−20.

[4] DEYMIER P A. Acoustic metamaterials and phononic crystals [M]. Berlin, Germany: Springer, 2013: 201−215.

[5] JOSE S D, GARCIA V M, DANIEL T, et al. Noise control by sonic crystal barriers made of recycled materials[J]. Journal of the Acoustical Society of America, 2011, 129(3): 1173−83.

[6] LIU Zhengyou, ZHANG Xixiang, MAO Yiwei, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734− 1736.

[7] PICHARD H, RICHOUX O, GROBY J P. Experimental demonstrations in audible frequency range of band gap tunability and negative refraction in two-dimensional sonic crystal[J]. Journal of the Acoustical Society of America, 2012, 132(4): 2816−2822.

[8] KOUSSA F, DEFRANCE J, JEAN P, et al. Acoustical efficiency of a sonic crystal assisted noise barrier[J]. Acta Acustica United with Acustica, 2014, 99(3) : 399−409.

[9] MORANDI F, MINIACI M, MARZANI A, et al. Standardised acoustic characterisation of sonic crystals noise barriers: sound insulation and reflection properties[J]. Applied Acoustics, 2016, 114: 294−306.

[10] ELFORD D P. Band gap formation in acoustically resonant phononic crystals[D]. Loughborough, UK: Loughborough University. Faculty of Science, 2010: 8−20.

[11] 李硕. 声子晶体在减振降噪中的应用基础研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2012: 8−16.LI Shuo. Fundamental research of phononic crystal and application to vibration and noise reduction[D]. Harbin: Harbin Institute of Technology. School of Mechatronics Engineering, 2012: 8−16.

[12] 张佳龙, 姚宏, 杜军, 等. 基于局域共振型声子晶体在机舱内低频隔声特性[J]. 硅酸盐学报, 2016, 44(10): 1440−1445.ZHANG Jialong, YAO Hong, DU Jun, et al. Low Frequency sound insulation characteristics of the locally resonant phononic crystals in the large aircraft cabin[J]. Journal of the Chinese Ceramic Society, 2016, 44(10): 1440−1445.

[13] YUAN Bo, CHEN Yong, JIANG Min, et al. The interaction of resonance and bragg scattering effects for the locally resonant phononic crystal with alternating elastic and fluid matrices[J]. Archives of Acoustics, 2017, 42(4): 1−8.

[14] 吴九汇, 马富银, 张思文, 等. 声学超材料在低频减振降噪中的应用评述[J]. 机械工程学报, 2016, 52(13): 68−78.WU Jiuhui, MA Fuyin, ZHANG Siwen, et al. Application of acoustic metamaterials in low-frequency vibration and noise reduction[J]. Journal of Mechanical Engineering, 2016, 52(13): 68−78.

[15] VASSEUR J O, DJAFARIROUHANI B, DOBRZYNSKI L, et al. Complete acoustic band gaps in periodic fibre reinforced composite materials: the carbon/epoxy composite and some metallic systems[J]. Journal of Physics Condensed Matter, 1999, 6(42): 8759.

[16] REINKE C M, SU M F, OLSSON R H, et al. Realization of optimal bandgaps in solid-solid, solid-air, and hybrid solid-air- solid phononic crystal slabs[J]. Applied Physics Letters, 2011, 98(6): 055405.

[17] 杨鹏, 唐剑, 易强, 等. 新型一维气−固周期型隔声板的带隙特性研究[J]. 铁道建筑, 2017, 57(12): 141−145. YANG Peng, TANG Jian, YI Qiang, et al. Band gap characteristics of a new-type one-dimensional gas-solid periodic sound insulation board[J]. Railway Engineering, 2017, 57(12): 141−145.

[18] CHEN Zeguo, WU Ying. Tunable topological phononic crystals [J]. Physical Review Applied, 2016, 5(5): 054021-1−9.

[19] 朱晓辉, 李隆球, 张广玉, 等. 基于层状周期性结构的声波调控技术研究[J]. 机械工程学报, 2017, 53(6): 10−15.ZHU Xiaohui, LI Longqiu, ZHANG Guangyu. Investigation of acoustic manipulation by layered periodic composites[J]. Journal of Mechanical Engineering, 2017, 53(6): 10−15.

[20] 刘启能. 一维声子晶体中声波能带的解析研究[J]. 应用力学学报, 2011, 28(2): 185−188. LIU Qineng. Analytical method of studying the phononic bandgap in 1D phononic crystal[J]. Chinese Journal of Applied Mechanics, 2011, 28(2): 185−188.

[21] DENG Yongquan, XIAO Xinbiao, HE Bin, et al. Analysis of external noise spectrum of high-speed railway[J]. Journal of Central South University, 2014, 21(12): 4753−4761.

[22] 杨新文, 王金, 练松良. 轨道交通轮轨噪声研究进展[J]. 铁道学报, 2017, 39(9): 100−108.YANG Xinwen, WANG Jin, LIAN Songliang. Review on wheel/rail noise in rail transit[J]. Journal of the China Railway Society, 2017, 39(9): 100−108.

[23] 李小珍, 杨得旺, 高慰, 等. 高速铁路半、全封闭声屏障振动与降噪效果研究[J]. 噪声与振动控制, 2018, 38(Z1): 8−13.LI Xiaozhen, YANG Dewang, GAO Wei, et al. Study on vibration and noise reduction of semi- or fully-enclosed noise barriers of high speed railways[J]. Noise and Vibration Control, 2018, 38(Z1): 8−13.

Band gap properties and noise reduction performances of periodic noise barriers in rail transit

YI Qiang1, 2, WANG Yuhang1, 2, GAO Xin1, 2, ZHAO Caiyou1, 2, WANG Ping1, 2

(1. Key Laboratory of High-speed Railway Engineering of Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China;2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Based on the band gap theory of phononic crystal, the air-solid periodic noise barrier was proposed. The transfer matrix method was used to study the acoustic band gap characteristics of the periodic sound barrier according to the Bloch principle, and the band gap was verified by the finite element model. The effects of density, sound velocity and filling rate of solid material on band gap were studied. The performances of the erect and fully enclosed periodic sound barriers on wheel-rail noise control were analysed by inputting the measured wheel-rail noise. The results show that larger density of solid material can significantly reduce the starting frequency, increase the cut-off frequency and broaden the bandwidth. When the filling rate of solid material is 0.5, the minimum starting frequency can be obtained, and the cut-off frequency increases with the increase of the filling rate. Compared with ordinary erect sound barrier of the same mass, the noise reduction of periodic sound barrier increases by 2−3 dB, while noise reduction of the fully enclosed sound barrier increases by 3−5 dB after the band gap is introduced.

rail transit; phononic crystal; sound barrier; band gap; noise control

U211.3

A

1672−7207(2019)05−1263−08

10.11817/j.issn.1672−7207.2019.05.031

2018−06−16；

2018−08−16

国家重点研发计划项目(2016YFE0205200)；国家自然科学基金资助项目(51508479)；四川省重点研发项目(2017GZ0373) (Project(2016YFE0205200) supported by the National Key Research and Development Program of China;Project(51508479) supported by the National Natural Science Foundation of China;Project(2017GZ0373) supported by the Key Research and Development Program of Sichuan Province)

赵才友，博士，副教授，从事轨道交通减振降噪研究；E-mail: zcy848279@163.com

(编辑 伍锦花)