利用物理学佯谬 展现科学魅力①

王丽军 刘莎莎 卢慕稚

(1. 北京师范大学良乡附属中学，北京 102488；2. 首都师范大学教师教育学院,北京 100048)

1 认识物理学佯谬

1.1 物理学佯谬概述

佯谬通常是指人们从某种假说出发进行逻辑推理却得出了与事实不符的结论，但一时很难确定问题的所在。是作为出发点的假说有错误,还是推理过程不够正确，有缺陷？在物理学发展史中，物理学佯谬有着让人难以抗拒的吸引力，促使物理学家们用他们的智慧和毅力去破解，推动了物理学的发展，也使人们感受到物理学的魅力。

1.2 物理学佯谬对科学发展的促进作用

(1) 佯谬是科学发展的直接动因之一。佯谬所揭示的原有体系的逻辑矛盾正是孕育新思想、推进物理学发展的科学问题。这类科学问题所揭示的往往是科学原有体系的内在逻辑矛盾，问题会十分尖锐，甚至有可能使原有的科学体系发生动摇，而这正是物理学能够不断发展的积极推动力之一。

(2) 佯谬中蕴含的逻辑推理方式，起着反驳和证明的作用。在对佯谬的分析过程中，佯谬其实就可以作为一种推理方式，进而解决其中的矛盾点，从而起到反驳和证明的作用。

(3) 佯谬具有方法论的功能。佯谬的产生、解决过程展示了科学家独特的思维方式，他们能够敏锐地抓住现有理论中的逻辑矛盾，用富有逻辑的推理或理想实验去论证推导，得出自相矛盾的命题。通过对物理佯谬产生和消除过程的分析，我们可了解物理学家创造性的思维过程，如何寻找矛盾，找到佯谬，然后如何从疑难中找到出路，将错误转向正确，从失败获得成功，因此佯谬具有某种程度上的方法论功能。

2 物理学佯谬的教育价值

2.1 介绍科学家对佯谬的不懈探索，培养学生求真的科学态度

核心素养导向的教学要求关注学生科学态度和价值观的形成。结合科学史中佯谬问题的教学，既符合人类认识规律，又富有趣味性，会加深学生对知识的认识：没有任何一个概念、规律可以被视为终极真理，人们在有限时空范围内获得的物理知识只能是近似的、相对的真理，科学的大厦只能完善，却永远不会封顶。同时还有助于消除学生对概念来源的“神秘感”，让学生体会到物理学在其发展的过程中凝聚的丰富的人文精神——求真精神、审美追求等，这些珍贵的人文精神在科学史上闪耀着光芒。

(1) 鼓励学生独立思考

物理学佯谬矛盾点的存在及冲突，可能正是学生物理学习中在遇到问题时陷入迷茫之处，我们可以利用物理学佯谬中的矛盾及冲突让学生有独立思考的机会。

(2) 鼓励学生养成持之以恒的科学态度

每一个物理佯谬的解决都会经历一段非常曲折、艰难的过程，在对每一个佯谬的思考研究过程中，科学家不断追求真理，孜孜不倦的精神也会引导学生逐渐养成持之以恒的科学态度。

2.2 科学家解决佯谬之道对学生起了良好的示范作用

(1) 鼓励学生提出质疑

带领学生重演科学家们解决佯谬的历程，鼓励他们像科学家一样进行猜想，并对假设进行质疑，然后寻找证据支持自己的观点，最终理解佯谬的解决过程。

(2) 提升学生的科学思维能力

利用物理学佯谬进行教学，使学生能够提出问题，运用分析综合、推理论证等方法解决问题，提升学生的科学思维能力。

3 利用物理学佯谬开展科学教育的实践

3.1 有选择地介绍物理上的经典佯谬

爱因斯坦说过：“结论几乎总是以完成的形式出现在读者面前。读者体会不到探索和发现的喜悦，感觉不到思想形成的主动过程，也很难达到清楚地理解全部情况”。在教学中引入物理学佯谬，可以弥补上述的遗憾，同时也丰富了教学内容。在教学实践中利用佯谬有以下两个途径。

(1) 在课堂教学实践中穿插物理学经典佯谬，促进知识理解，开阔学生思路

现在高中物理所讲的大部分内容都是经典物理学，学生对现代物理学了解得很少。所以在高中物理教学中恰当地穿插物理学经典的佯谬，不仅可以促进学生对知识的理解，还可以开阔学生思路。比如在自由落体的教学中，可以介绍“落体佯谬”；讲究热力学第二定律后，可以穿插“麦克斯韦妖”和“热力学第二定律与时间箭头之谜”；在讲完光的波粒二象性后，可以介绍“波粒二象性佯谬”“薛定谔猫”等。

教学中要注意佯谬的选择要适度，要和所学知识有联系，并根据学生情况对其中难度较大的部分进行适当的删减。实施的方式可多样化，比如可以提供材料让学生去阅读、发现问题，让学生去讨论，或者设计系列问题引导学生尝试解决。总之要增加学生思维的参与度，不能仅仅是教师的简单介绍。

(2) 开设讲座或校本课程，让学生了解物理学佯谬，激发兴趣，发展思维

相对集中介绍物理学中的佯谬，让学生对于佯谬的产生及解决过程中蕴含的科学方法有比较系统的了解，而且所选内容比较多样，不受课堂知识所限。笔者曾经以“物理学佯谬”为题，为学生做了一次讲座，讲座中选取了比较通俗易懂而且比较有意思的经典佯谬，比如“奥伯斯佯谬(光度学佯谬)”“麦克斯韦妖”“薛定谔猫”等。讲座当天讲堂中座无虚席，同学们怀着对知识的渴求、对未知事物的好奇，随着教师一起进入科学的探秘之旅。

学生听完讲座后在学校的公众号上写道：“佯谬在科学史中，既体现了科学方法、科学思维的教育，也再现了历史上科学伟人科学态度的严谨和对真理追求的精神，更展示了科学伟人们人格上的伟大与平凡。”

这种教学实施方式也可以多样化，比如可以开设校本课程，充分发挥学生的积极性、主动性，多给学生时间，让学生不断探索，在解决问题的过程中发展学生思维，还可以让学生选择比较喜欢的内容做研究性学习。

3.2 学生在学习过程中出现的悖论是丰富的教学资源

学生在物理学习的过程中，也会出现一些悖论。这些悖论的产生原因很多，可能是对概念理解存在偏差，或没有明确定律的适用条件，或分析问题的逻辑混乱等。老师恰当地引导和释疑，对于学生深入理解概念、规律，提高思维能力，具有十分重要的意义。

比如，在讲解行星的变轨问题时，学生会出现类似例1的问题。

例1：如图1所示，发射地球同步卫星时，先将卫星发射至近地圆轨道1，然后经点火使其沿椭圆轨道2运行，最后再次点火，将卫星送入同步轨道3，轨道1、2相切于Q点，轨道2、3相切于P点，试判断：

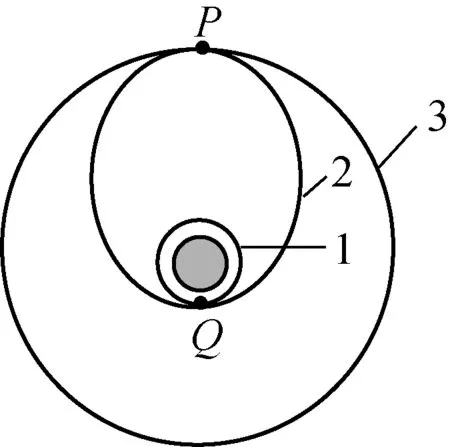
图1

(1) 卫星在轨道3上的速率与在轨道1上的速率关系；

(2) 卫星在轨道1上经过Q点时加速度与它在轨道2上经过Q点的加速度的大小关系。

解析：对第(1)问有两种分析思路：一是卫星从圆轨道1到轨道3经历了两次点火，卫星在轨道3上的速率应该比在轨道1上的速率大；二是根据圆周运动的规律分析卫星在轨道3上的速率反而比在轨道1上的速率要小。因此产生了悖论，造成这个悖论的原因为：(1) 在第二种分析方法中,学生对卫星全过程的分析缺少了椭圆部分的速度变化。卫星在椭圆轨道2上从Q点到P点速度是减小的，到达P点时，如果不加干预，卫星会沿着椭圆轨道回到Q点。整个过程是变速运动，满足开普勒第二定律。(2) 高中不要求推导卫星做椭圆运动的条件，学生不理解为什么在Q点加速之后会沿着椭圆轨道运动，为什么从P点又会回到Q点。(3) 高一讲解这部分内容时，还没有学习机械能守恒定律，对于动能和势能的转化关系学生还不太理解。不知道两次点火之后是总的机械能增加了，但势能的增加量大于机械能的增加量，动能反而是减小的。

对这个悖论的讨论会加深学生对椭圆运动的认识和对开普勒第二定律、能量守恒定律的理解。当然这个讨论可以对不同层次的学生有不同的要求，程度好一点的学生可以增加卫星做椭圆运动的条件及其引力势能等知识，从理论上更好地理解这个问题。

对第(2)问也有两种分析方法：一是根据牛顿第二定律，从受力的角度判断加速度大小关系。因为卫星无论是在哪个轨道上，只要在Q点，地球对卫星的万有引力不变，加速度大小相等；另一种分析方法是根据圆周运动的向心加速度公式来判断，因为卫星在Q点经加速进入轨道2，Q点离地心的距离不变，所以卫星在轨道1上经过Q点时加速度小于它在轨道2上经过Q点的加速度。

两种分析所依据的理论都是正确的，但是学生对向心加速度公式中r的理解存在偏差，当物体做椭圆运动时r应为曲率半径，而曲率半径此时不等于引力半径。轨道2上Q点处的曲率半径应大于引力半径，对其定量关系在高中阶段不作要求，只能用第一种分析方法去解释。造成这个悖论的原因在于学生对研究非圆周问题的一般曲线运动时的分析方法理解不深入，对公式中各字母的确切含义不清楚。

从上面例子可以看出，学生在学习过程中产生的“悖论”一般有下面的特点：对同一问题用不同的原理或分析方法往往会得出两种不同的结论，他们的推导似乎逻辑严密，论据充分，但结论又互不相容，或者根本就是对立的，由于在比较中必然会产生疑问，从而可以使学生产生迫切解决矛盾的求知动力。

4 结语

笔者在物理教学中通过多种方式利用物理学佯谬和学生学习过程中产生的“悖论”,效果很好。学生有解决问题的强烈渴望，跃跃欲试，而且对现代物理中的内容也非常感兴趣。因此在教学中恰当地运用佯谬，鼓励学生勇敢提出自己的困惑，并能够找出足够的证据来支持自己的观点，在解决疑惑的过程中不断探索尝试，可以培养学生的科学思维能力，提高学生的核心素养。