看历年《选修3—3》高考试题定2019年备考复习重点

■山东省博兴第二中学 田家富

一、近五年高考对《选修3—3》考查情况的统计

表1

二、命题特点

从近五年的高考试卷统计可以看出，分子动理论、气体压强的微观解释、晶体与非晶体的特点、液体的表面张力、饱和汽与饱和汽压、热力学第二定律的理解、理想气体各物理参量间的图像关系等考点，常常以五选三选择题的形式出现，评分标准采用的是选对1个得2分，选对2个得4分，选对3个得5分；每选错1个扣3分，最低得分为0分。气体实验定律和状态方程的应用常常以计算题的形式出现，往往涉及一部分气体或关联的两部分气体，依托活塞、液柱、图像等要求利用力的平衡条件计算气体的压强，利用活塞、液柱的移动现象，以及数学中的几何关系求解变化前后气体的体积，题目形式基本固定，侧重考查考生的综合分析推理能力和数学运算能力，但有时也会出现综合性较强、物理量较多、变化过程较复杂的题目，同学们在备考复习中应加以重视。

三、命题趋势和应对策略

预计2019年高考对本部分内容的考查仍会由热学基础知识组成选择题，由气体实验定律相关知识命制计算题，难点仍体现在气体压强的计算、体积的变化、过程的确定这几个方面上。另外，为了突出物理核心素养，还会出现以科技前沿、社会热点及与生产生活联系的问题为情境的题目，以考查考生提取物理信息，创建物理模型，利用气体实验定律和状态方程相关知识求解实际问题的能力。解答选择题，需要抓住本部分内容的基础，强化理解性记忆，明确选择题的得分方法，确保得到基础分5分。解答计算题，应该遵照该部分内容的解题步骤，养成善于画图（气体的状态图、几何图等）、确定状态参量、充分利用几何关系找体积、对关联物体（活塞、液柱等）正确进行受力分析、列共点力作用下物体平衡方程求压强等方法和策略，争取得到满分10分。

四、高频考点能力突破

1.考查分子动理论、内能及热力学定律等基础知识的保分类试题。

（1）估算问题：

③两种分子模型：

立方体模型：V=a3（适用于估算气体分子间距）。

（2）反映分子运动规律的两个实例：

表2

（3）对热力学定律的理解：

①改变物体内能的方式有两种，只叙述一种改变方式是无法确定内能变化的。

②热力学第一定律ΔU=Q+W中W和Q的符号可以这样确定：只要此项改变对内能增加有正贡献的即为正，反之为负。

③对热力学第二定律的理解：热量可以由低温物体传递到高温物体，也可以从单一热源吸收热量全部转化为功，但不引起其他变化是不可能的。

例1（2018·全国Ⅱ卷）对于实际的气体，下列说法中正确的是____。

A.气体内能包括气体分子的重力势能

B.气体内能包括分子之间相互作用的势能

C.气体内能包括气体整体运动的动能

D.气体体积变化时，其内能可能不变

E.气体内能包括气体分子热运动的动能

解析：气体的内能等于所有分子热运动的动能和分子之间势能的总和，故选项A、C错，B、E对。根据热力学第一定律ΔU=W+Q可知，改变内能的方式有做功和热传递，气体的体积发生变化时，其内能可能不变，选项D正确。

答案：BDE

例2（2017·全国Ⅰ卷）氧气分子在0℃和100℃温度下单位速率间隔的分子数占总分子数的百分比随气体分子速率的变化分别如图1中两条曲线所示。下列说法中正确的是____。

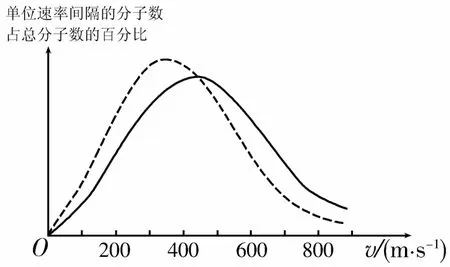
图1

A.图中两条曲线下面积相等

B.图中虚线对应于氧气分子平均动能较小的情形

C.图中实线对应于氧气分子在100℃时的情形

D.图中曲线给出了任意速率区间的氧气分子数目

E.与0℃时相比，100℃时氧气分子速率出现在0～400m/s区间内的分子数占总分子数的百分比较大

解析：温度是分子平均动能的标志，温度升高，分子的平均动能增加，不同温度下相同速率的分子所占比例不同，温度越高，速率大的分子所占比例越高，故虚线是0℃对应的曲线，实线是100℃对应的曲线，曲线下的面积都等于1。

答案：ABC

例3（2016·全国Ⅰ卷）关于热力学定律，下列说法中正确的是____。

A.气体吸热后温度一定升高

B.对气体做功可以改变其内能

C.理想气体等压膨胀过程一定放热

D.热量不可能自发地从低温物体传到高温物体

E.如果两个系统分别与状态确定的第三个系统达到热平衡，那么这两个系统彼此之间也必定达到热平衡

解析：气体吸热后，若再对外做功，则温度可能降低，选项A错误。改变气体内能的方式有两种，即做功和热传递，选项B正确。理想气体等压膨胀的过程是吸热过程，选项C错误。根据热力学第二定律可知，热量不可能自发地从低温物体传到高温物体，选项D正确。如果两个系统分别与状态确定的第三个系统达到热平衡，那么这两个系统彼此之间也必定达到热平衡，否则就不会与第三个系统达到热平衡，选项E正确。

答案：BDE

2.考查固体、液体、气体和物态变化等基础知识的保分类试题。

（1）晶体和非晶体：

表3

（2）液晶的性质：液晶是一种特殊的物质，既可以流动，又可以表现出单晶体的分子排列特点，在光学性质上表现出各向异性。

（3）液体的表面张力：使液体表面有收缩到球形的趋势，表面张力的方向跟液面相切。

（4）饱和汽压的特点：液体的饱和汽压与温度有关，温度越高，饱和汽压越大，且饱和汽压与饱和汽的体积无关。

（5）相对湿度：某温度时空气中水蒸气的实际压强与同温度水的饱和汽压的百分比。

（6）气体状态参量：

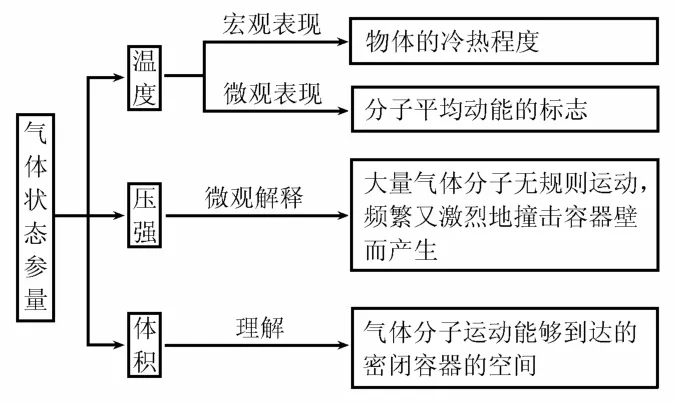
例4（2018·全国Ⅲ卷）如图2所示，一定质量的理想气体从状态a变化到状态b，其过程如p-V图中从a到b的直线所示。在此过程中____。

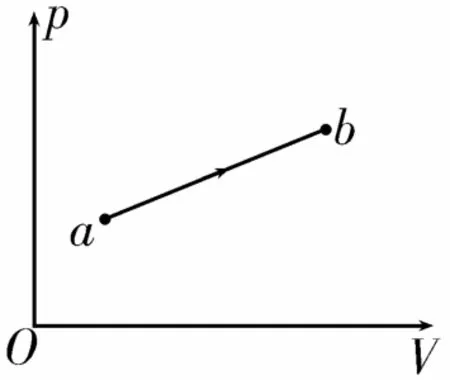
图2

A.气体温度一直降低

B.气体内能一直增加

C.气体一直对外做功

D.气体一直从外界吸热

E.气体吸收的热量一直全部用于对外做功

解析：一定质量的理想气体从状态a变化到状态b的过程中，由理想气体的状态方程可知，T＞T，即气体的温度ba一直升高，选项A错误。根据理想气体的内能只与温度有关可知，气体的内能一直增加，选项B正确。因为从状态a到状态b的过程中气体的体积增大，所以气体一直对外做功，选项C正确。根据热力学第一定律ΔU=W+Q可知，从状态a到状态b的过程中气体一直从外界吸热，选项D正确。气体吸收的热量一部分用于增加内能，一部分用于对外做功，选项E错误。

答案：BCD

3.考查气体实验定律和理想气体状态方程等多维探究类知识的试题。

（1）压强的计算：研究被活塞封闭在汽缸内的气体时，通常分析活塞或汽缸的受力情况，应用平衡条件求解；研究被液柱封闭在细管内的气体时，通常分析液柱的受力情况，应用平衡条件求解。

（2）强化记忆气体实验定律和状态方程：等温变化，玻意耳定律，公式为p1V1=p2V2；等容变化，查理定律，公式为；等压变化，盖-吕萨克定律，公式为；理想气体的状态方程，公式为。

（3）利用气体实验定律及状态方程解决问题的基本思路：

题型一：“活塞”模型

求被活塞封闭气体的压强时，一般以活塞为研究对象，分析它受到的气体压力及其他各力，列出力的平衡方程，求解压强。如图3所示，活塞静止于内壁光滑的汽缸中，活塞质量为m，横截面积为S，被封闭气体的压强为p，大气压强为p0，则活塞的受力情况如图所示，由平衡条件得pS=p0S+mg，解得p=p0+。

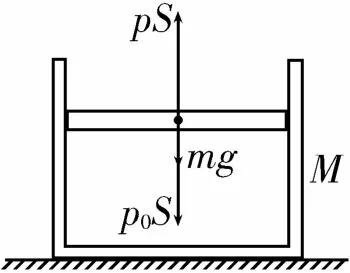
图3

例5（2018·全国Ⅱ卷）如图4所示，一竖直放置的汽缸上端开口，汽缸壁内有卡口a和b，a、b间距为h，a距缸底的高度为H；活塞只能在a、b间移动，其下方密封有一定质量的理想气体。已知活塞质量为m，面积为S，厚度可忽略；活塞和汽缸壁均绝热，不计它们之间的摩擦。开始时活塞处于静止状态，上、下方气体压强均为p0，温度均为T0。现用电热丝缓慢加热汽缸中的气体，直至活塞刚好到达b处。求此时汽缸内气体的温度及在此过程中气体对外所做的功。重力加速度为g。

图4

解析：因为活塞处于平衡状态，所以可以利用平衡条件求出封闭气体的压强，然后找到不同状态下气体参量，计算温度或体积。

开始时活塞位于a处，加热后，汽缸中的气体先经历等容过程，直至活塞开始运动。设活塞刚开始运动时汽缸中气体的温度为T1，压强为p1，根据查理定律得，根据力的平衡条件得p1S=p0S+mg，解得。此后，汽缸中的气体经历等压过程，直到活塞刚好到达b处，设此时汽缸中气体的温度为T2，活塞位于a处和b处时气体的体积分别为V1和V2，根据盖-吕萨克定律得，式中V=SH，V=S（H+12h），解得。从开始加热到活塞刚好到达b处的过程中，封闭气体对外做的功W=（p0S+mg）h。

题型二：“液柱”模型

求被液柱封闭气体的压强时，一般以液柱为研究对象进行分析受力，列平衡方程。注意：①液体因重力产生的压强大小p=ρgh（其中h为至液面的竖直高度）；②不要漏掉大气压强，同时又要尽可能平衡掉某些大气的压力；③有时可以直接应用连通器原理——连通器内静止的液体，同种液体在同一水平面上各处压强相等；④当液体为水银时，可灵活应用压强单位“cmHg”等，使计算过程简捷。

例6（2016·上海卷）如图5所示，两端封闭的直玻璃管竖直放置，一段水银将管内气体分隔为上下两部分A和B，上下两部分气体初始温度相等，且体积VA＞VB。

（1）若A、B两部分气体同时升高相同的温度，水银柱将如何移动?

某同学解答如下：

图5

上述解答是否正确?若正确，请写出完整的解答；若不正确，请说明理由并给出正确的解答。

（2）在上下两部分气体升高相同温度的过程中，水银柱位置发生变化，最后稳定在新的平衡位置，A、B两部分气体始末状态压强的变化量分别为ΔpA和ΔpB，分析并比较二者的大小关系。

解析：（1）不正确。水银柱移动的原因是升温后，压强变化造成受力平衡被破坏，因此应该假设气体体积不变，由压强变化判断移动方向。

（2）升温前有pB=pA+ph（ph为水银柱压强），升温后同样有pB′=pA′+ph，两式相减得ΔpA=ΔpB。

题型三：“两团气”模型

求解多个系统相互联系的定质量气体问题时，往往需要以压强建立起系统间的关系，确定各个系统的变化性质，分别应用相应的实验定律列式求解各个系统的压强、体积、温度等物理参量。

例7（2018·全国Ⅲ卷）如图6所示，在两端封闭、粗细均匀的U形细玻璃管内有一股水银柱，水银柱的两端各封闭有一段空气。当U形管两端竖直朝上时，左、右两边空气柱的长度分别为l1=18.0cm和l2=12.0cm，左边气体的压强为12.0cmHg。现将U形管缓慢平放在水平桌面上，没有气体从管的一边通过水银逸入另一边。求U形管平放时两边空气柱的长度。在整个过程中，气体温度不变。

图6

解析：设U形管两端竖直朝上时，左、右两边气体的压强分别为p1和p2，U形管水平放置时，两边气体压强相等，设为p，此时原左、右两边气体长度分别变为l1′和l2′，如图7所示。由平衡条件得p1=p2+ρg（l1-l2），式中ρ为水银密度，g为重力加速度。由玻意耳定律得p1l1=pl1′，p2l2=pl2′，l1′-l1=l2-l2′。联立以上各式解得l1′=22.5cm，l2′=7.5cm。

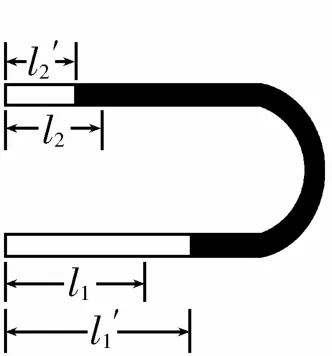
图7

题型四：异类题型

此类型试题涉及的知识、方法等综合性较强，求解时不能局限于常规的“气体实验定律和理想气体状态方程”的方法，思路要开阔，方法要灵活。

例8（2016·全国Ⅰ卷）在水下气泡内空气的压强大于气泡表面外侧水的压强，两压强差Δp与气泡半径r之间的关系为，其中σ=0.070N/m。现让水下10m处一半径为0.50cm的气泡缓慢上升。已知大气压强p0=1.0×105Pa，水的密度ρ=1.0×103kg/m3，重力加速度大小g=10m/s2。

（1）求在水下10m处气泡内外的压强差。

（2）忽略水温随水深的变化，在气泡上升到十分接近水面时，求气泡的半径与其原来半径之比的近似值。

解析：（1）当气泡在水下h=10m处时，设其半径为r1，气泡内外压强差为Δp1，则。

（2）设气泡在水下10m处时，气泡内空气的压强为p1，气泡体积为V1；气泡到达水面附近时，气泡内空气的压强为p2，气泡内外压强差为Δp2，气泡体积为V2，半径为r2。气泡在上升过程中温度不变，根据玻意耳定律得p1V1=p2V2，由平衡条件得p1=p0+ρgh+Δp1，p2=p0+Δp2，气泡的体积V1和V2分别为，解得。因为Δp≪p，i=i01，2，所以可略去上式中的Δpi项。代入数据解得。