逆断层作用下埋地管道局部屈曲行为研究
张 杰,陈小华,鲁 鑫,彭昀飞
1.西南石油大学机电工程学院,四川 成都 610500;2.石油天然气装备教育部重点实验室,四川 成都 610500;3.中国石油天然气股份有限公司西南管道分公司,四川 成都 610094
引 言
石油、天然气既是重要能源又是战略资源,油气安全直接关系着国民经济的发展和国家安全。作为油气资源最经济、快捷、可靠的输送方式,管道系统被称为生命线工程。管道的结构可靠性与安全问题逐渐受到广泛关注[1]。截至2017年底,全球石油与天然气管道的总里程已超过233.0×104km,其中,原油管道56.2×104km,成品油管道35.1×104km;天然气管道142.5×104km[2-3]。长输油气管道主要采用埋地敷设,因而地层对管道的影响较大,同时管道沿线的各种地质灾害极易影响其结构安全,特别是管道发生屈曲、断裂等失效行为,导致的油气泄露事故,不但造成环境污染,而且容易引发爆炸、火灾等安全事故,威胁人民生命与财产安全[4]。地层运动造成的地面永久变形是导致管道发生失效的主要原因之一,如1994年美国北岭地震导致大量油气管道破裂,引发了数百起火灾;1999年土耳其因伊兹米特7.8级地震,造成管道破裂,导致大量原油泄漏并引发火灾;1996年云南丽江发生7.0级地震,导致多处供水管道破裂、爆管;2002年阿拉斯加发生7.9级地震,造成输油管道支持系统出现10多处破坏[1]。因而,对跨断层油气管道的力学研究对管道敷设、检测评估、维修防护等具有重要意义和实践指导价值。
目前,断层作用下埋地管道的理论研究主要是基于弹性地基梁模型。Newmark和Hall于1975年首次提出应用静态土压力和静态摩擦力的小位移模型分析断层错动对地下管道影响的理论方法[5]。随后,Kennedy等考虑管土的相互作用,改进了Newmark-Hall方法,通过大位移理论对管道弯曲应变进行了计算[6]。Wang和Yeh考虑了管土作用与管道抗弯刚度,将其假定为弹性地基梁和大变形梁,应用管道钢三折线本构模型,分析了管道应变应力[7]。Chiou将变形管道简化为弹性体和半无限梁模型,建立理论模型[8]。Karamitros等基于弹性梁模型和弹性地基梁计算了断层两侧管道的变形[9]。随着计算机仿真技术的发展,有限元方法在管道力学研究中得到广泛应用。如侯忠良等基于弹性地基梁,采用有限元法和虚功原理建立了管道平衡方程并进行了求解[10];张进国等采用断层作用下管道有限元方程,求解了管道应力和位移[11];郭恩栋、Tohidi等采用梁单元和弹簧单元,研究了断层运动对管道力学的影响[12-13];刘爱文等采用边界有限元法计算了土耳其地层对供水管道的影响[14];Vazouras等基于接触模型研究管土相互作用,同时采用壳单元仿真研究了断层区管道力学响应[15-17];王滨建立了管道等效边界管壳单元有限元模型,研究了管道应力应变[1]。
国内外许多学者对不同断层作用下的管道理论模型进行了研究,但是理论模型和数值模型的研究大多集中在弹性阶段,而对埋地管道在断层作用下的塑性问题及发生局部屈曲失效模型的研究相对较少,且忽略了内压对管道局部屈曲的影响。为此,建立了跨断层区埋地管道的管土耦合数值计算模型,重点研究了埋地钢管发生局部屈曲以后的失效形貌,对管道出现压溃和起皱现象的原因进行了深入分析。
1 跨断层管道解析模型
1.1 Newmark-Hall方法
图1所示为Newmark-Hall方法计算模型(其中,Δ-断层错动的总位移,m;β-管道与断层之间夹角,(°),fs—直管道摩擦力,N;L-管道长度,m)。
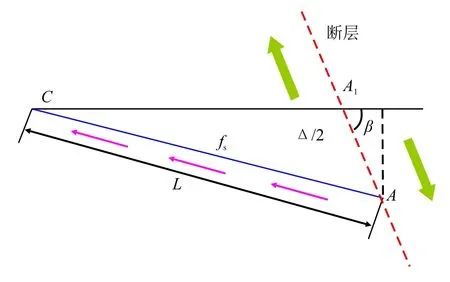
图1 Newmark-Hall方法计算模型Fig.1 Calculation model of Newmark-Hall method
管道采用三折线应力应变模型,其中,A点为断层与管道交点,C点为管道内应变为0的点。该方法忽略了围土横向作用力和管道弯曲变形,仅考虑轴向的管土摩擦力[5]。应用迭代法可对管道最大应变进行求解,并与管材的许用应变进行对比,进而对管道的破坏情况进行判断。
1.2 Kennedy方法
美国油气管道抗震设计规范(ASCE,1984)采用Kennedy方法来对管道应力进行计算,图2所示为计算模型(其中,fp—圆弧段管道所受的摩擦力,N;pp—圆弧段管道处的压力,N;Ls—直管道长度,m;Lc1—圆弧段管道的水平投影长度,m)。图2中,B为变形管道与初始管道相交的交点,其靠近断层面,AB管段为圆弧,BC管段为直线。该模型假定最大应变位置出现在与断层相交点。

图2 Kennedy方法计算模型Fig.2 Calculation model of Kennedy Method
1.3 Wang-wang及张素灵方法
1983年,Leon Ru-Liang Wang和Yaw-huei Yeh考虑管道刚度与弯曲应变,远离断层面位置采用弹性地基梁模型,断层附近假定为圆弧管段,进而提出了一种更为精细的求解方法,其计算模型如图3所示(其中,q直管道处的压力,N)。该方法认为管道的最大应力不一定在断层处,可能在其附近的某个点上。

图3 Wang-wang及张素灵分析模型Fig.3 Calculation model of Wang-wang and Zhang Method
基于Wang-Wang模型,2000年,张素灵采用Ramberg-Osgood管材钢模型,提出了一种可将Newmark-Hall和Kennedy模型作为特例的新方法[14]。假定变形管道为反对称结构,断层面两侧土质相同,可只对一侧建模分析。整个管段可分AB段和BC段。A点为断层面与管道交点;B点为两段分界点,但该点随夹角和位错量的变化而变化;C点为锚固点,且该处内应力为0。
虽然理论解析模型可对管道的应变、位移等进行预测,但其存在局限性。
(1)管道是一种薄壁壳结构,叠加原理不适用于管道大变形的求解,跨断层油气管道易发生局部屈曲失效,梁模型和索模型很难描述其屈曲形貌特征,且管道变形后产生的残余应力与应力集中也很难通过理论研究求解。
(2)理论解析模型只适用于管道受拉工况,而实际工程中埋地管道受力非常复杂,很难通过解析模型进行求解。
(3)许多管道模型研究未考虑介质内压作用[16],忽略了内压对跨断层埋地管道屈曲模式的影响,而数值仿真计算为研究油气管道局部屈曲提供一种较好的方法,可模拟管道屈曲特征。
目前,中国使用的《油气输送管道线路工程抗震技术规范》(GB 504702008),要求对于重要区段及位于强震区的管道应使用有限元方法进行抗震校核,其他情况下使用Newmark-Hall计算结果的2倍修正值进行校核。
2 断层区管道数值模型
2.1 数值计算模型
建立跨断层埋地管道三维计算模型如图4所示。

图4 计算模型示意图Fig.4 Schematic diagram of the numerical model
以逆断层为例,断层面倾角 30°;管道直径 813 mm,管材为 X80,壁厚 8 mm,屈服强度 596 MPa,管道承受最大内压(其中,σy—屈服极限,MPa;t—管道壁厚,m;D—管道直径,m)[16]。软土地层中假定地层土与回填土相同,均采用Mohr-Coulomb弹塑性本构模型描述岩土物理特性,参数为:泊松比0.44,弹性模量33 MPa,摩擦角 11.7°,黏聚力 24.6 kPa,密度 1 400 kg/m3;管道埋深2 m。
对地层与回填土采用实体单元划分网格,对管道采用壳单元划分网格,对管土接触部位网格进行细化。定义管土接触关系,设置接触表面之间的摩擦系数为0.3。
2.2 数值模型验证
台湾集集地区于1999-09-11发生了7.6级大地震,断层运动导致了地表局部破裂,许多燃气PE管发生破坏。该PE管的弹性模量200 MPa,泊松比为0.44,管材弹塑性屈服应变0.06,屈服应力12 MPa,塑性屈服应变0.2,塑性屈服应力19 MPa[18]。
建立相应的数值计算模型,以集集地震中由垂直逆冲断层引起的PE管破坏为例进行计算,计算得到管道最大轴向压缩应变为0.088 6,PE管的实际最大轴向压缩应变为0.091[18],本文数值模型结果与实测结果的误差仅为2.6%。因此,所采用的壳单元模型与数值建模方法较为可靠。
3 内压对管道局部屈曲影响
逆断层作用下,埋地管道最先发生弹性变形,而后出现塑性变形,随着断层位错量的进一步增加,管道出现局部屈曲。图5所示为埋地管道发生局部屈曲前后的管土变形情况。

图5 局部屈曲发生前后的管土变形Fig.5 Deformation of soil and pipe before and after buckling
由图5可知,管道出现局部屈曲以前,整个管道发生弯曲变形后仍为光滑曲线;而当局部屈曲发生后,整个管道变形曲线由S形变为Z形。管道形变过程中,并非与围土始终保持接触,特别是断层面附近的管段仅有一侧与围土接触,而另一侧与围土之间形成空隙;由于管道变形,围土与各部分管道之间接触力沿轴向并非均匀分布,因而埋地管道与围土之间的摩擦力并非均匀分布,在埋地管道大变形计算中采用理想管土摩擦力亦不再适宜。由于埋地管道上部回填土的厚度相对下部地层较薄,当地层发生逆断错动时,断层面两侧的管道变形并非呈对称或反对称分布;在管道作用下,下盘区地面出现了较为严重的隆起现象,而上盘区地面并未出现隆起;两个局部屈曲部位距离断层面的距离也不相同,上盘区管道局部屈曲部位距离断层较近,而下盘区的屈曲部位距离较远。
图6为断层位错量为3.5D时,不同介质内压作用下管道应力分布与局部屈曲模式。
整个管道出现了两处局部屈曲部位,这两处管段为应力集中区,而非屈曲部位管段的应力随着内压的增大而增大。由管道局部放大图可知,无压管道和低压管道在逆断层作用下的局部屈曲模式为压溃,而随着内压的增大,管壁屈曲模式由压溃变为起皱,且内压越大,管道的起皱幅度越大。因而,内压是影响管壁局部屈曲模式的最主要因素。通过对比可知,上盘区管道的局部屈曲幅度较下盘区更为严重,因而上盘区的管段更早发生失效。上盘区局部屈曲管段与断层面之间的距离随内压变化较小;而下盘区管道处于压溃模式下,该部位与断层面之间的距离随着内压的增大而减小;管壁局部起皱模式下,下盘区局部屈曲部位管段与断层面之间距离随着内压的增大而减小。当内压为8.4 MPa时,在上盘区管段局部屈曲部位的外侧,也出现了一处应力集中,但其出现在起皱部位的另一侧。
断层运动使得埋地管道承受较大的弯矩及轴向载荷,从而造成管壁出现局部屈曲。由分析结果可知,管道出现局部屈曲部位的轴向应变最大,而最大轴向应变集中在上盘区局部管壁屈曲部位,且最大压应变大于拉应变。图7所示为管道最大轴向应变随内压变化曲线(u—断层位错量,m)。
由图7可知,不同地层位错量下的管道轴向应变随内压变化规律不同。无论何种压力管道,地层位错量大于3D时,管道轴向应变迅速增大,说明该工况下管道出现了局部压溃或起皱。当管道内压小于 0.6pmax(pmax—最大内压,MPa)时,管道轴向应变随内压的增大而增大。当管道内压大于0.6pmax,地层位错量小于4D时,管道轴向应变随着内压的升高而增大;而当位错量大于4D时,管道轴向应变随着内压的升高而减小。这是由于地层位错量较大时,高压管道的局部屈曲部位的外侧又出现了应力集中,从而缓解了屈曲部位的起皱幅度,因而管道初始屈曲部位的最大轴向应变有所降低。

图6 不同内压管道的应力分布及局部屈曲模式Fig.6 Stress distribution and the local buckling mode of the pipe with different pressures
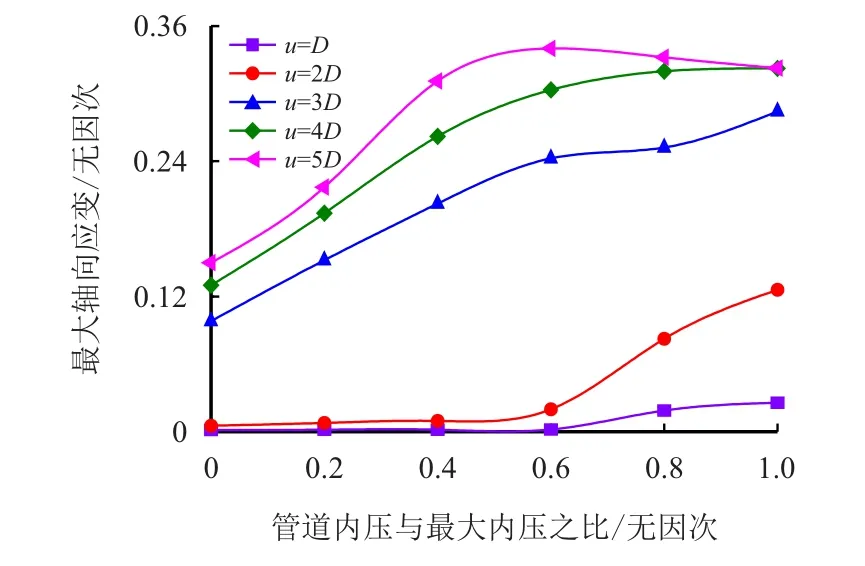
图7 管道最大轴向应变随内压变化曲线Fig.7 The maximal axial strain curve with internal pressure
4 位错量对管道局部屈曲影响
地层位错量越大,其对埋地管道产生的附加载荷就越大,管道的变形也越严重。图8为不同位错量下的无压管道应力分布及局部屈曲模式(图中管道上的标注为错位量)。随着位错量的增大,无压管道的应力集中越严重,而远离断层面的管段不受地层运动的影响,其应力为0;位错量小于管道直径D时,无压管道仅发生弹性变形,应力集中区域也较小。

图8 无压管道应力分布及局部屈曲模式Fig.8 Stress distribution and the local buckling mode of the non-pressure pipe
由图8可见,随着位错量的增大,在断层面两侧的管壁逐渐发生塑性变形,并出现压溃形貌,且压溃幅度随位错量的增大而越发严重;两个屈曲部位之间的管段逐渐被拉伸,但该段中间部位的应力却逐渐减小;两个部位管壁出现的压溃模式相同,但上盘区管段压溃形貌较下盘区更为严重。
当管道内压为0.6pmax时,管道应力分布及局部屈曲模式如图9所示。

图9 压力管道应力分布及局部屈曲模式Fig.9 Stress distribution and the local buckling mode of the pressure pipe
当位错量小于D时,整个管段均未出现应力集中现象,说明内压作用下管道的初始应力较大。随着位错量的增大,应力集中现象出现在断层面两侧的管段,当管道发生弯曲变形时,受压侧管段的应力集中范围大于受拉侧。随着断层位错量的逐渐增大,两处应力集中部位的管壁出现了起皱现象,且起皱幅度随着位错量的增加而逐渐增大,且上盘区管段的起皱幅度大于下盘区管段。压力管道的变形曲线由S形变为Z形,在两个局部屈曲部位出现了拐点。
图10所示为埋地无压和压力管道最大轴向应变随位错量的变化曲线。当位错量小于1.23D时,无压管道和压力管道均未发生塑性变形,因而管道的轴向应变变化非常小;随着位错量的增大,管道的轴向应变增长率逐渐增大,且压力管道的增长率大于无压管道。当位错量为1.97D时,压力管道轴向应变发生突变,而无压管道轴向应变发生突变的临界位错量为2.21D,说明这两种工况下的管道均出现了局部屈曲。随着位错量的进一步增大,管道的轴向应变先以较大的速率增大,而后变化率逐渐减小。由于内压的作用,压力管道的最大轴向应变大于无压管道。

图10 埋地管道最大轴向应变随位错量变化曲线Fig.10 The maximal axial strain curve with fault displacement
5 径厚比对管道局部屈曲影响
径厚比影响管道的抗变形能力,当内压为5.1 MPa,位错量为3.5D时,不同径厚比管道的应力分布如图11所示(其中,图中管道上的标注为径厚比)。

图11 不同径厚比管道应力分布Fig.11 Stress distribution and the pipe with different diameter-thick ratios
由图11可见,相同内压作用下,管道径厚比越大,管壁上的应力越大。随着管道径厚比的减小,埋地管道的局部屈曲现象逐渐消失,而呈现出两个范围较大的应力集中区域。上盘区管道的应力集中区位置随管道径厚比的变化较小,而下盘区管段的应力集中区随着径厚比的减小而逐渐远离断层面。因而,断层作用下的薄壁管道更容易出现局部屈曲,增加壁厚可降低管道的局部变形。
压力管道的最大轴向应变随其径厚比变化曲线如图12所示。不同地层位错量作用下,管道最大轴向应变随径厚比的变化规律不同。当断层量为D时,管道轴向应变随径厚比变化非常小;当断层量为2D,径厚比大于100时,管道的最大轴向应变随着径厚比的增大而迅速增大;当断层量为3D时,管道轴向应变随着径厚比的增大而增大,但变化率是先增大后减小;当断层量大于3D时,管道轴向应变随着径厚比的增大呈先增大后减小趋势变化,这是由于局部屈曲部位的外侧又出现了一处应力集中,缓解了屈曲部位的起皱幅度。因而,断层量越大,管道壁厚越薄越容易出现局部压溃或起皱。
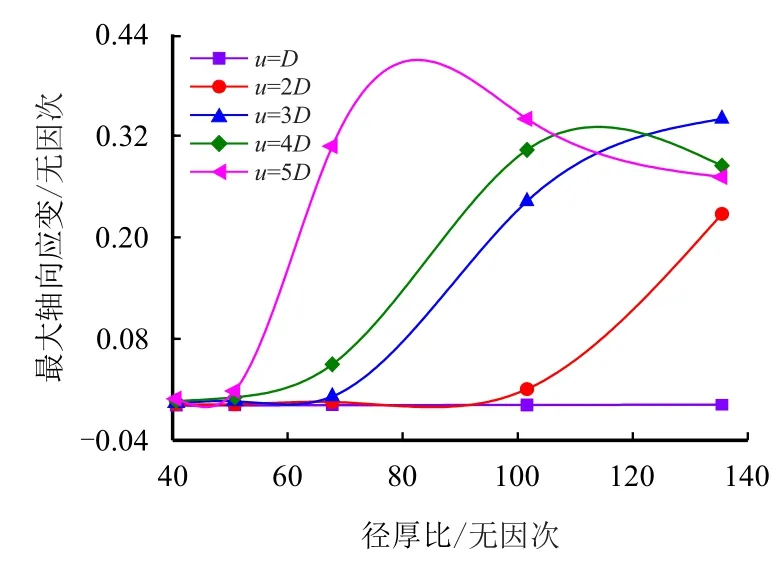
图12 埋地管道最大轴向应变随径厚比变化曲线Fig.12 The maximal axial strain curve with diameter-thick ratio
6 结 论
(1)逆断层作用下,埋地管道变形过程中其外表面并非与围土完全接触,断层面附近管段仅一侧与围土接触,而另一侧与围土之间形成空隙,且断层面两侧的管道变形并非呈对称或反对称分布,上盘区的管道屈曲现象较下盘区更为严重;断层面两侧的管段出现了两处应力集中,随着位错量的增大逐渐演化为局部屈曲,埋地管道变形曲线由S形变为Z形。
(2)逆断层作用下无压管道和低压管道的局部屈曲模式为压溃,而随着内压的增大,管壁屈曲模式由压溃变为起皱,且管道起皱幅度随着内压的增大而增大;压溃模式下,两个屈曲部位之间的距离随着内压的增大而减小;起皱模式下,二者之间的距离随着内压的增大而增大,但上盘区管段屈曲部位与断层面之间距离受内压、径厚比影响较小;随着径厚比的减小,管道屈曲幅度逐渐减小。

