注采不平衡与套损力学机理研究

罗泽利，练章华，李长平，3，林铁军，何 勇

（1中海石油（中国）有限公司深圳分公司2西南石油大学3大港油田公司采油三厂）

罗泽利等.注采不平衡与套损力学机理研究.钻采工艺，2019，42（5）：5-8

在油气开采过程中，若注采不平衡必然造成储层地层压力快速衰减，上部岩层的荷重部分转移到岩石骨架上，使得岩石骨架的有效应力增大，从而导致储层孔隙压实，地表沉降。储层压实、地表下沉对油气生产和套管造成了诸多不利的影响［1］。1992年，Bruno M［2］用有限元方法建模对因储层压实导致的套管失效进行了研究，指出地层的垂向变形会导致套管挤压和弯曲失效；地层的水平变形可能导致套管的剪切和弯曲失效；而水平变形的剪切和弯曲失效实际上比垂向变形造成的弯曲和挤压失效要平常和严重。经研究，地表下沉位移在开采的井筒附近最大，呈碗状、漏斗状下沉［3-4］。2002年，A Settari［5］对储层压实机理进行了分析，指出通过维持地层压力（保持孔隙度不变），可以防止储层压实，地面下沉，当被压实后，再恢复压力来补救是十分有限的。其次是通过注水维持地层压力也是预防储层压实的措施之一。李结实等［6］，张俊等［7］研究了油气开采合理的注采比，如果注采比不合理，必将引起地层的升降，可能导致套损，合理的注采比也是维持井筒完整性的措施之一。2003年，A Abou-Sayed等［8］建立了地质模型研究了储层压实和地表下沉，并分析了井眼附近的地层变化情况，为研究储层压实对套管的影响奠定了基础。张春会［9］，朱庆川等［10］利用不同的数学分析方法，如岩体力学方法一维固结理论和比奥三维固结理论，层次分析法等分析导致地面沉降的原因，从而找到地面下沉的影响因素。2005年，罗敏等［11］通过实际油田数据建立了空间地应力与地位移计算模型，通过有限元的模拟，得到了开采后不同孔隙流体压力作用下各储层的变形和地表沉降位移，结果表明，底水引起的地表沉降位移最大。2006年，C.Sayers等［12］用3D地质力学模型评估了因储层压实、地面沉降造成的套管变形，为地面沉降造成的套损研究提供了参考。2010年，穆伟刚等［13］对开采诱发地表沉降的预测方法进行了研究，并指出了每种预测方法的优缺点。为实际工程中预测地表移动和变形提供了参考。同年，包修瑞［14］建立了地表沉降检测模型，研究了岩石蠕变参数对沉降的影响，结果表明蠕变岩石对沉降有较大的影响。2015年，陈兴贤等［15］运用比奥固结理论，建立有限元数值模型，研究了地下水开采及高层建筑荷载叠加影响下的地面沉降特征。LY Chin等［16］用完全耦合和不完全耦合方法研究了地质和储层多相流体之间的相互作用，指出岩石浸水后容易引起储层压实和下沉。并指出上覆岩层压力时在储层压实因素方面扮演了重要的角色。专家学者们对储层压实、地面下沉的研究，为研究其对套管受力的影响奠定了方法和理论基础。在前人研究的基础上，建立套管-水泥环-地层三维有限元模型，研究因注采不平衡导致地层亏空，储层压实，地表下沉时套管的力学行为，为研究井筒完整性和防控因储层压实造成的套损措施提供理论依据。

一、注采不平衡地层套损的理论分析

在油气开采过程中，由于注采不平衡使得储层孔隙压力变化，导致储层压实，地表下沉。为计算储层压实量及地表变化量，首先假设压缩只发生在垂向上，假设储层垂直压缩量为Δh，则：

式中：h—储层原始的厚度；Cm—储层岩石的单轴压缩系数；Δp—储层压力改变量。

为研究因储层压实、地表下沉对套管的影响，假设套管与水泥环，水泥环与地层之间没有发生滑动，且大部分轴向应变发生在储层，地层压缩系数为常数，则轴向应变为：

套管的临界应变为0.3% ～0.7%，按最低临界应变来算，则使套管失效的临界储层压力变化量为：

而通常套管与水泥环、水泥环与地层之间界面会发生滑动，这样使得实际的套管垂向变形量会小于地层的垂向变形量。

当地表下沉时，因套管外水泥环或地层限制不足，套管就会在轴向载荷下产生弯曲变形。假设套管与水泥环、水泥环与地层之间没有发生滑动，而最小套管的弯曲载荷为：

式中：Ac—套管的横截面积；Ec—套管的弹性模量。

二、有限元分析

1.有限元模型

由于注采不平衡，开采过程储层地层压力和地应力的作用下，使套管发生屈曲变形，剪切或挤压破坏。该地质条件下不能简化为平面问题和轴对称问题，只能建立三维空间的有限元力学模型，有限元实体模型和网格模型见图1和图2所示。研究时采用外径为139.7 mm，壁厚为7.72 mm的N80钢级套管进行模拟，图1中压力p为上覆地层压力p1与注采不平衡引起的压力p2之和。如果采出较多，则地层亏空、向下沉陷，套管被压缩屈曲变形，p2与p1同方向；如果注入较多，则地层被上台或断层活动滑移，套管被剪切变形，p2与p1方向相反。官104油藏埋深2 606～2 799 m，储层段因注采不平衡，地层压力下降，储层压实，地表下沉，导致套管严重损坏。该油藏最大、最小水平地应力分别为51.3 MPa和42.39 MPa，上覆岩层压力为60.86 MPa。

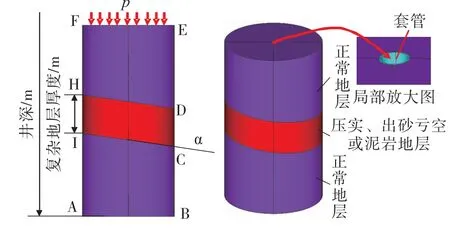
图1 有限元实体模型

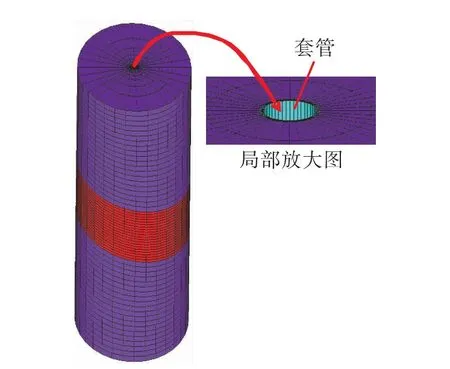
图2 有限元网格模型

2.注采不平衡引起套管损坏的有限元结果分析

研究注采不平衡（特指注少采多）的套损机理，根据本研究建立的有限元力学模型，用ANSYS有限元软件进行模拟计算，得到地层亏空、储层压实、地表下沉引起套管力学行为的模拟结果。

2.1 亏空段地层下沉位移

在实际开采中，储层的压实情况比较复杂，且不易测量，能测到的是地表下沉量，因此，通过所建立的模型，以地表下沉量为已知条件反算储层的压实量。

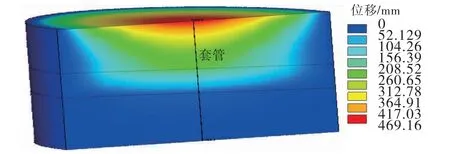
图3 地表下沉3 182.7 mm时储层段地层位移分布

图3为地表下沉3 182.7 mm时，储层段地层下沉位移分布云图，由图3可知，最大储层位移在井筒附近，最大位移达469.16 mm。地层的垂向位移将导致套管弯曲和挤压变形。

2.2 亏空段套管的侧向位移

图4是地表下沉不同的位移时，储层段套管的侧向位移等值线分布云图。由图4可知，当储层压实，地表下沉造成套管呈“S”型变形，并且随着地表下沉深度增加，最大侧向位移也增大，套管的弯曲变形更严重，当地表下沉为3 182.7 mm时，亏空段套管最大的侧向位移达到16.954 mm。而变形越大，套管承载能力减弱，在上覆岩层压力下，更易发生套损。

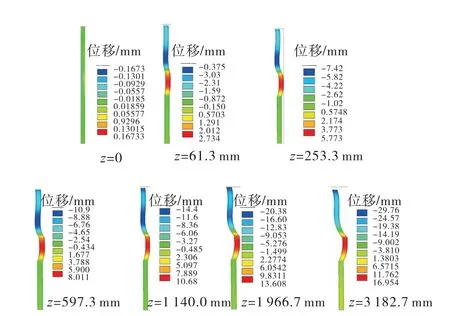
图4 地表下沉不同的位移时，亏空段地层套管的侧向位移等值线分布

2.3 亏空段套管内的应力

图5为地表下沉3 182.7 mm时，亏空段地层套管内Von Mises应力等值线分布云图，由图5可知，在储层段，由于上覆岩层压力的作用，地表下沉，p2与p1同方向，将储层孔隙压实，套管被压缩屈曲变形。从图5可见，在亏空段，套管内最大的Von Mises应力为563.63 MPa，超过了N80的屈服应力551 MPa，因此，在地层亏空，压实段套管已发生塑性破坏。

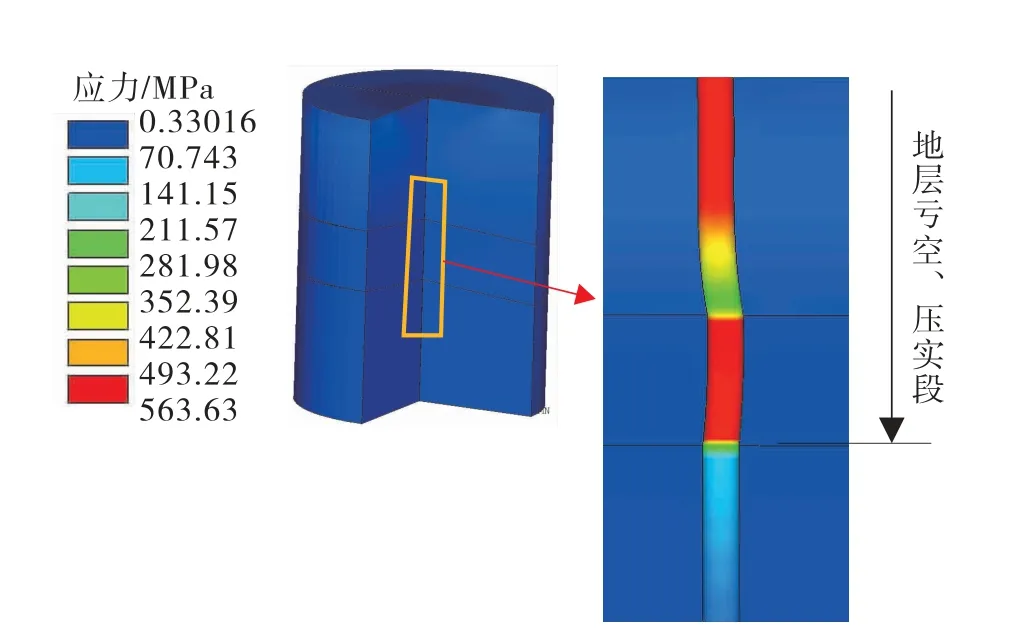
图5 地表下沉3 182.7 mm时亏空段地层套管内Von Mises应力等值线分布云图

2.4 泥岩水化、不同地面下沉量亏空段套管的位移及应力分析

当泥岩水化后，其弹性模量下降，使其侧向支撑能力下降，在较弱的侧向支撑下，套管在亏空段更易变形。由图6可知，当储层压实，地表下沉造成套管呈“S”型变形，并且随着地表下沉深度增加，侧向位移也增大，此外，随着泥岩水化程度增大，套管的侧向位移也增大。由图7可知，不同地面下沉量的套管应力在同一地层层位变化不大；当地表下沉量相同时，在地层亏空压实段套管应力迅速增大，并在亏空段达到最大应力，并且随着地层水化程度的增加，即亏空段地层弹性模量的降低，套管的应力增大，当E2＝2.27×103MPa时，亏空压实段套管的应力超过了N80套管的屈服强度。

图6 不同泥岩水化程度下套管的侧向位移曲线

图7 不同泥岩水化程度下套管的应力曲线

三、结论

（1）因注采不平衡导致地层亏空，在亏空段套管发生了相反的侧向位移，即套管发生了“S”型变形破坏，并且随着地表下沉深度的增加，套管侧向位移增大。

（2）因注采不平衡导致地层亏空，在亏空压实段套管应力最大，因此，在亏空压实段容易发生套损。

（3）在相同的地表下沉量时，随着水化程度的增加（弹性模量降低），套管的应力和位移均增大，因此，若注采不平衡，泥岩水化会加剧套损。

（4）提高钢级有利于防控因注采不平衡造成的套损。