紧抓三视图构造 突破面到体难点——《观察物体（三）》教学实践

□ 谢纯涨 南欲晓

“观察物体（三）”是人教材五年级下册第一单元的教学内容。它包含两个例题，例题1是根据从一个方向看到的平面图，用给定数量的小正方体摆出相应的几何组合体。例题2是根据从三个方向看到的平面图，用小正方体摆出相应的几何组合体。

【学情分析】

观察物体，学生已经积累了丰富的生活经验和学习经验。学生在第一学段经历过从不同角度观察实物和单个立体图形以及几何组合体的学习，能根据物体的特征抽象出几何图形，会分辨从不同方向观察立体图形得到相应的平面图形，已经初步建立了从三维立体图形中抽象出二维平面图形的能力。

在现场采用互动交流方式与不同学习能力层次的学生进行交流，发现部分学生能够根据三个方向的平面图形想象立体图形，但不能表达自己的思考过程。

【教学目标】

1.能从一个面或几个面的视图想象相应的几何体。

2.经历观察、想象、操作和推理等过程，积累活动经验，提高空间想象能力，发展空间观念。

3.参与游戏、拼摆等数学活动，感受数学的趣味性，培养学习兴趣。

【教学重难点】

根据观察到的平面图形想象或摆出相应的立体图形。

【过程设计】

一、借“穿墙术”情景，体验“体”与“面”的联系

1.情境：“魔法方块”穿墙游戏。把两个如图摆放的立方体（作为一个整体）置于长方体内（见下图）。

2.想象：当它分别平行于长方体的棱从正面、右面、上面穿过时，会在这些面上留下什么样的痕迹？

3.小结：不同的面上留下的痕迹可能是不一样的。

（设计意图：情境可以激发学生的学习兴趣，以形象的“墙”作为载体，可以帮助学生搭建“面”与“体”转换的想象“桥梁”。）

二、想象还原，感悟从“面”到“体”的变化

层次一：研究“一个面”，感悟“体”的多样性。

1.一个面——正面（正视图）。

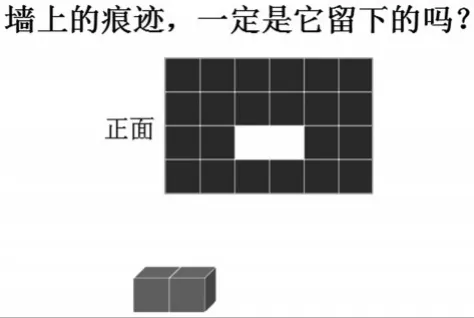
（1）设疑：墙上镂空的痕迹，一定是这两个立方体“穿越”时留下的吗？

学生一开始认为只有2个，慢慢地，在想象过程中发现立方体的个数可以不同。

（2）想象：立方体增加，体会摆法的多样性（学具操作）。

（3）小结：（课件演示）立方体不管增加几个，不管是往前摆还是往后摆，只要从正面看到的图形是一样的，都可以。

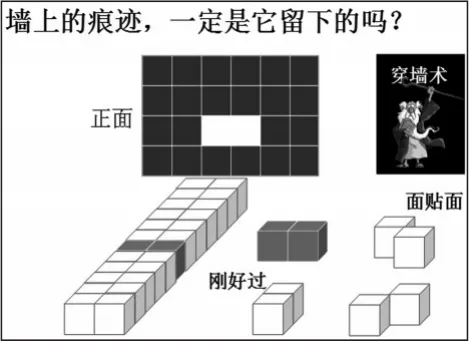
（4）研究两个方块的摆法：想象一下，两个立方体还能摆出什么样子呢？

出示一些其他摆法。2.一个面——右面（右视图）。

过渡：刚才我们研究了正面，右面的墙上留下了这样的痕迹，是怎样留下的呢？

想象：引导学生想象，感悟有多种摆法。

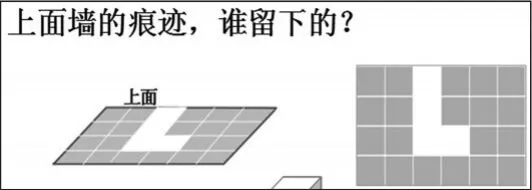
3.一个面——上面（俯视图）。

同样处理。

4.小结：当我们只知道一个面的形状时，能摆出的立方体组合有多种可能性。（板书：一个面→多种可能性）

（设计意图：在“穿过一面墙”活动中，学生经历观察、想象、猜测、分析和推理的过程，为后续“多面墙”的想象积累基本活动经验。）

层次二：研究“两个面”，感悟“体”受制约。

1.想象：如果“体”既穿过正面又穿过右面，它长什么样的呢？

2.操作：学生用学具摆出自己想象出的形状，在操作过程中初步体会有不同的摆法。

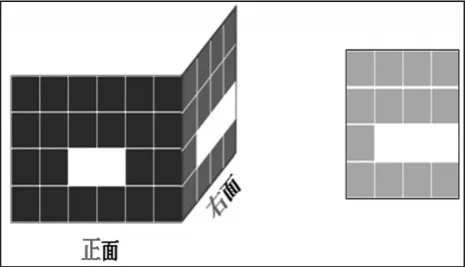
3.验证：引导学生验证自己的摆法是否同时满足两个要求。

4.引导：①先确定正面，再想右面；②先确定右面，再想正面。（课件展示，帮助学生想象）

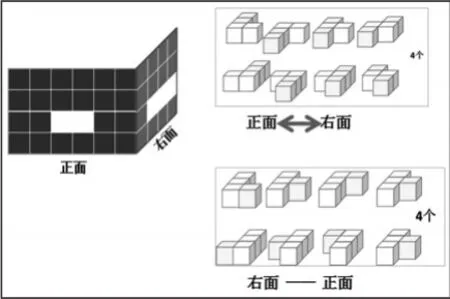
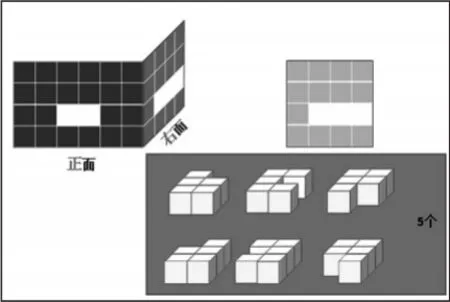
5.辨析：感悟2个视图之间相互联系和制约的关系。

（1）质疑：满足两个面的要求最多只能摆6个立方体吗？

（2）想象：如果在6个立方体的基础上再加一个会怎样？

利用学具演示，引导学生想象，在前后、左右、上下再加一个立方体后视图的变化。

（3）小结：再加一个立方体，都会影响两个面的图形。

（4）想象：在6个的基础上我想拿掉一些，但还同时满足两个面的要求，可以怎样减？（课件展示，帮助学生想象）

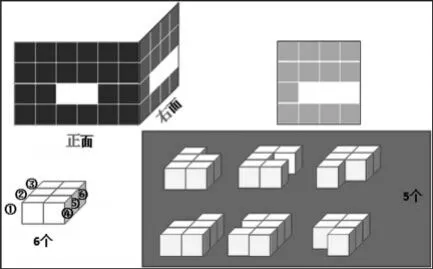
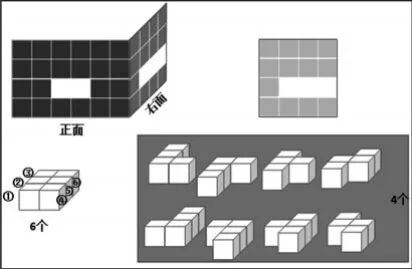
（设计意图：让学生在研究立方体个数和位置的变化与调整中，感受“2个方向”的面的确定的立方体的个数还是有多种情况，而且立方体个数相同，摆法依然是丰富的。）

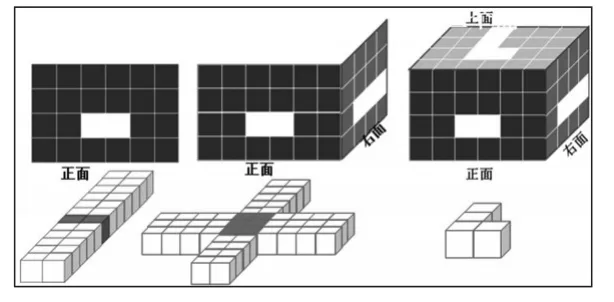
层次三：研究“三个面”，体会“体”的确定性。

1.设疑：我们刚才研究了两个面的情况，发现摆的结果比一个面时少了很多（板书：两个面→可能性减少），如果想确定形状的话，还需要什么条件？

2.想象：上面也来了，要同时满足三个面，摆出来又是怎样的？

3.操作：在刚才满足两个面的摆法的基础上进行操作，感悟调整的过程。

4.验证：引导学生验证自己的摆法是否同时满足三个面的要求，并进行调整。

5.展示、交流：这次大家摆的都是一样的。（课件展示正确摆法）在摆的时候有什么诀窍吗？（引导学生反馈调整的过程）

6.小结：在两个面的基础上，根据第三个面对方块的个数和位置进行调整。三个面确定了，物体的形状也就确定了。（板书：三个面→确定形状）

层次四：回顾梳理，体会“体”确定的过程。

1.回顾：只有一个面的时候，我们能想象的摆法有无数种。当有两个面的时候，可能性就减少了。如果有三个面的话，就能帮助我们确定形状了。

2.演示：结合语言梳理，利用课件动态演示，可能性逐渐减少，直到确定形状的过程。

（设计意图：经历由一个面、两个面到三个面的想象体的结构的过程，体会思维的发展，体会“从无数种到少很多再到唯一”的因果本质。）

三、深化认知，进一步感悟“面”与“体”的联系

1．基础训练，感悟用“三个面”确定“体”。

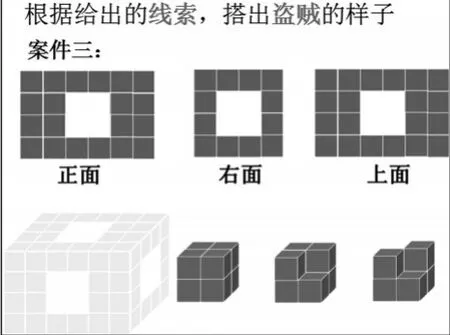
（1）素材：给定三个面的形状，结合“抓盗贼”的游戏情境，根据“面”的线索，想象“体”的形状。

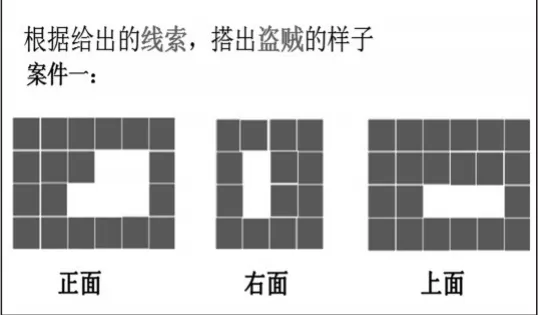
（2）想象：这个盗贼长什么样呢？

（3）小结：三个面的图形能帮助我们确定物体的形状。

2.变式想象，感悟确定形状的过程。

（1）素材：根据两个面想象“体”。

（2）想象：至少需要几个立方体能满足这两个面的要求？

（3）展示：利用课件动态展示先确定正面，再满足右面的想象过程。

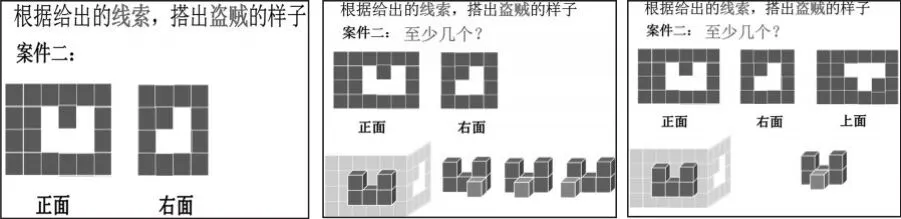
（4）追问：想确定形状的话还需要什么条件？（上面）

3.提升训练，打破思维定式。

（1）素材：三个视图形状相同想象“体”。

（2）想象：现在立体图形又长什么样呢？

（3）操作：引导学生用立方体摆出来，在摆的过程中体会“体”的多样性。

（4）反馈：在交流的过程中，引导学生理解立方体个数和位置的变化不会影响视图。利用课件动态演示，感悟在特殊情况下，三个面也不能确定形状，打破思维定式。

（设计意图：分三个层次进行练习，基本练习，变式练习，提升练习，让学生感受根据平面视图想象出所描述的实际物体，在“体”与“形”的抽象和还原活动中，感悟平面图形与立体图形之间的联系。）

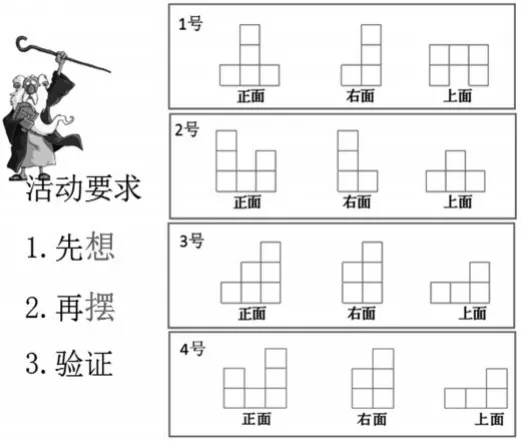
4.综合训练，自主作业。

学生自主完成活动：在图中选择一题，经历想象、操作、验证、调整的过程。