基于D-H的柔性焊接机械手运动学分析与仿真

朱红娟

[摘           要]  柔性机械手运动学方程的建立是对其进行运动学分析的基础。应用D-H法建立机械手的运动学模型，通过机械手各构件关节变量求解出机械手末端执行器的空间位姿。在 Solidworks中完成焊接机械手的三维建模，利用ADAMS软件对机械手进行运动学仿真。结果表明，柔性机械手弹性变形对机械手的运动精度有较大影响，研究结果为柔性机械手运动学分析提供了基础。

[关    键   词]  机械手;运动学;ADAMS

[中图分类号]  TP241.3                [文献标志码]  A                       [文章编号]  2096-0603（2019）08-0232-02

在工业生产中，机器人被广泛应用于点焊、喷涂、搬运等生产环节。在以前的机械设计中，机器人系统运动学模型均设为刚性体。机械手柔性对其关键点的位移、速度、加速度等有一定影响，且杆件越长，柔性变形的影响越不可忽视。随着机器人技术的进步和生产高速、高效的发展，构件的弹性变形越来越受到重视，因此对柔性机械手的研究成为机器人领域研究的热点。以五自由度焊接机械手为模型，基于D-H理论对其运动学进行建模分析，利用Adams软件对柔性机械手进行运动学仿真研究，为进一步进行柔性机械手的动力学分析及运动规划提供了基础。

一、运动学分析

柔性机械手多采用浮动坐标系进行表示。并将坐标建立在关节处。

（一）机械手矢量表示

机械手的柔性引起的变形包括横向弯曲变形、纵向变形和扭转变形，下文仅考虑横向弯曲变形的影响。建立坐标系时将基座定位在机械手构件底端，设定为O0—X0Y0，每个杆件末端依次设定坐标系，i杆上的坐标为Oi—XiYi，末端位置为O5—X5Y5。θ1为腰部回转自由度，θ2为大臂俯仰自由度，θ3为小臂俯仰自由度，θ4为腕关节俯仰自由度，θ5为腕关节摆动自由度;l0为腰部高度，l1为大臂长度，l2为小臂长度，l3+l4为腕关节中心到焊枪末端的距离。五自由度机械手构件上任一点矢量，如图1所示。

u fi=？准i1（x1）qi1（t）+？准i2（x2）qi2（t）

式中：？准ij（xi）=sin（jπxi/li）——振型函數

（二）机械手运动学建模

在传统的刚性机械臂运动学分析中，以关节变量作为自变量求解机械臂末端执行器的位置和姿态，通常采用D-H法。对柔性机械臂而言，我们需要对D-H法作适当的扩展和延伸。

相邻构件坐标系之间的齐次变换矩阵分别为：

E=A1A2A3A4A5=nx ox ax pxny oy ay pynz oz az pz0  0  0  1

式中：px，py，pz分别为机器人末端执行器中心相对于基坐标系x，y，z方向的位移;第1，2，3列分别为机器人末端执行器中心相对于基坐标系x，y，z的方向余弦，并且有：

nx=c1c234c5-s1s5;ny=s1c234c5+c1s5;nz=s234c5;

式中：ci，si——cosθi和sinθi的简写符号。

式中：θi——电机驱动转动的理想角度;

F（t）——构件末端的纵向受力。

二、焊接机器人运动仿真

（一）运动学仿真模型的建立

ADMAS软件本身具有一定的三维建模能力，但建模功能相对于专业的CAD软件比较薄弱。故利用SolidWorks建立五自由度焊接机器人的三维模型，通过Solidworks将装配图另存为parasolid格式文件后导入ADAMS软件。在ADAMS环境下，赋予材料属性。根据机器人模型的实际运动情况，定义各个部件之间的运动约束。在进行相应设置后，为各个转动关节施加相应驱动，然后直接在Adams/View中建立柔性体的MNF文件。

三、机器人仿真分析

利用Adams进行刚体模型和柔性模型的动态响应求解，再利用两者之差求误差曲线。在Postprocessor中，对刚体模型和柔性模型中的相关数据进行比较。

1.末端执行器（机械手）位移变化曲线，如图2所示。通过位移变化曲线可以看出在第3s时，考虑柔性体和不考虑柔性时机器人末端的位置变化明显，约为0.6mm，这个误差已经不能忽略。

2.末端执行器（机械手）速度变化曲线，如图3所示。柔性体仿真数据始终以刚体仿真结果曲线为中心线波动，波动幅值较小;y方向速度差值最大值为0.7mm/s。

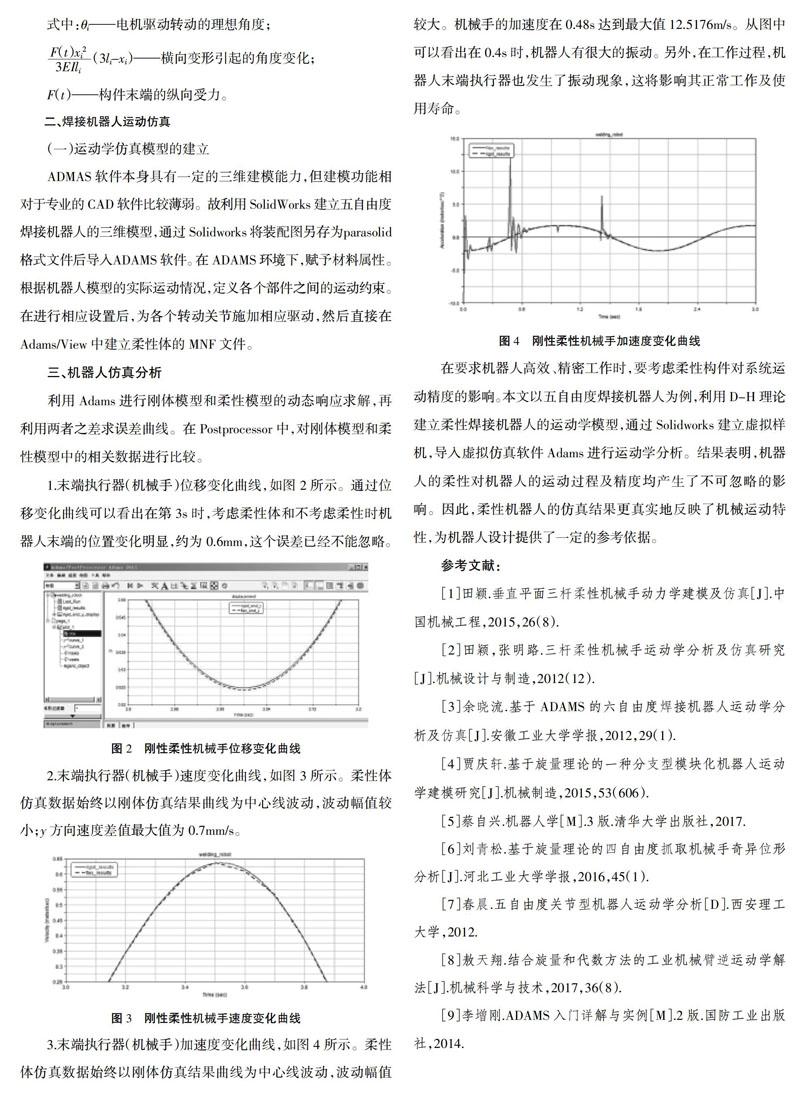
3.末端执行器（机械手）加速度变化曲线，如图4所示。柔性体仿真数据始终以刚体仿真结果曲线为中心线波动，波动幅值较大。机械手的加速度在0.48s达到最大值12.5176m/s。从图中可以看出在0.4s时，机器人有很大的振动。另外，在工作过程，机器人末端执行器也发生了振动现象，这将影响其正常工作及使用寿命。

在要求机器人高效、精密工作时，要考虑柔性构件对系统运动精度的影响。本文以五自由度焊接机器人为例，利用D-H理论建立柔性焊接机器人的运动学模型，通过Solidworks建立虚拟样机，导入虚拟仿真软件Adams进行运动学分析。结果表明，机器人的柔性对机器人的运动过程及精度均产生了不可忽略的影响。因此，柔性机器人的仿真结果更真实地反映了机械运动特性，为机器人设计提供了一定的参考依据。

参考文献：

[1]田颖.垂直平面三杆柔性机械手动力学建模及仿真[J].中国机械工程，2015，26（8）.

[2]田颖，张明路.三杆柔性机械手运动学分析及仿真研究[J].机械设计与制造，2012（12）.

[3]余晓流.基于ADAMS的六自由度焊接机器人运动学分析及仿真[J].安徽工业大学学报，2012，29（1）.

[4]贾庆轩.基于旋量理论的一种分支型模块化机器人运动学建模研究[J].机械制造，2015，53（606）.

[5]蔡自兴.机器人学[M].3版.清华大学出版社，2017.

[6]刘青松.基于旋量理论的四自由度抓取机械手奇异位形分析[J].河北工业大学学报，2016，45（1）.

[7]春晨.五自由度关节型机器人运动学分析[D].西安理工大学，2012.

[8]敖天翔.结合旋量和代数方法的工业机械臂逆运动学解法[J].机械科学与技术，2017，36（8）.

[9]李增刚.ADAMS入门详解与实例[M].2版.国防工业出版社，2014.