混合式钢混组合梁斜拉桥收缩徐变灰色分析

贾烊 黄新 李建慧 王涛

摘  要：为了研究混凝土收缩徐变对混合式钢混组合梁斜拉桥结构线形的影响，根据工程实际建立全桥空间有限元模型，基于AEMM-FEM法和灰色关联度方法分析混合式钢混组合梁斜拉桥的收缩徐变效应。结果表明：在收缩徐变的作用下，边跨混凝土主梁竖向变形微小，主跨钢混组合梁跨中下挠变形较大，随着运营时间的增加组合梁挠度不断发展。提高环境相对湿度、桥面板预制龄期和混凝土抗压强度后，组合梁的挠度值和塔顶偏移值均有所减小。由灰色关联度序列可知，混凝土抗压强度是影响组合梁线形的最敏感因素，环境相对湿度、混凝土收缩龄期和桥面板预制龄期的影响依次递减。塔顶变形受混凝土收缩龄期的影响最为严重，其次是混凝土抗压强度的影响。研究结论对减轻混合式钢混组合梁斜拉桥运营期间收缩徐变影响有一定的意义。

关键词：斜拉桥;组合梁;收缩徐变;灰色关联度;有限元法

中图分类号：U448.27 文献标识码：A 文章编号：1006-8023（2019）01-0075-05

Abstract： In order to study the effects of concrete shrinkage and creep on the line shape of the hybrid steel-concrete composite girder cable-stayed bridge， a full-bridge spatial finite element model was established according to the engineering practice. Based on AEMM-FEM method and gray correlation degree method， the effects of concrete shrinkage and creep of hybrid steel-concrete composite girder cable-stayed bridge were analyzed. The results show that the vertical deformation of the concrete girder is small due to the effects of shrinkage and creep， while the large deflection occurs in the steel-concrete composite girder and develops with the increase of the operation time. Increasing the relative humidity of the environment， the precast age of the bridge deck and the concrete compressive strength， the deflection of the composite girder and the longitudinal displacement of the top of the pylon are reduced. According to the gray correlation sequence， the compressive strength of concrete is the most sensitive factor affecting the line shape of the composite girder， while the effects of environmental relative humidity， shrinkage age of concrete and the precast age of the bridge deck are successively decreasing. The longitudinal displacement of the top of the pylon is most affected by the shrinkage age of concrete， followed by the compressive strength of the concrete. The research conclusion is of significance for alleviating the effects of shrinkage and creep during the operation of hybrid steel-concrete composite girder cable-stayed bridges.

Keywords： Cable-stayed bridge; composite girder; shrinkage and creep; gray correlation degree; finite element method

0 引言

混合式鋼混组合梁斜拉桥是指边跨采用混凝土梁，主跨采用钢混组合梁形式的斜拉桥。作为混凝土材料的固有时变特性，收缩徐变会在较长时间内引起混凝土结构不均匀变形、预应力钢筋松弛等问题[1-3]。为了计算混凝土结构的收缩徐变效应，研究者们基于试验结果提出了众多收缩徐变预测模型，其中常用的有CEB-FIP1990模型、B3模型等[4-5]。计算理论方面，Bazant基于线性叠加原理提出了按龄期调整的有效模量法（AEMM法）[6-7]，将此方法与有限单元步进法（FEM法）结合，可以计算混凝土结构的收缩徐变效应。

钢混组合梁常采用剪力钉等构件限制桥面板与钢梁间的相对位移，而混凝土收缩徐变变形受到约束后会在结构内部引起附加应力[8-9]，国内外学者对钢混组合梁的收缩徐变效应展开了广泛的研究。Ranzi等[10]假定混凝土面板与钢梁之间存在线性相对滑移，计算得到了钢混组合梁收缩徐变的解析解。樊健生等[11]对4根钢混组合梁进行了长期荷载试验，按CEB-FIP1990模型计算得到的挠度理论值与试验实测值基本吻合。刘沐宇等[12]利用试验结果建立了高抗裂致密匀质混凝土收缩徐变预测模型，对港珠澳大桥钢混组合连续梁桥进行了长期时变效应分析。关于混合式钢混组合梁斜拉桥的文献资料主要集中在钢混结合段受力分析、结构抗震分析等方面[13-14]，已有文献对此类桥型的收缩徐变效应缺乏相应的研究。众多工程案例表明，混凝土收缩徐变容易导致斜拉桥几何变形超限，影响桥梁的安全使用与行车舒适性[15]。本文基于AEMM-FEM法计算混合式钢混组合梁斜拉桥的收缩徐变效应，利用灰色关联度方法分析收缩徐变参数对结构线形影响的敏感性差异。

1 工程背景

某独塔双索面混合式钢混组合梁斜拉桥全长333 m（51 m+92 m+190 m），预应力混凝土主梁宽42.5 m，钢混组合梁宽42 m，为塔墩梁固结体系。主塔采用H型钢筋混凝土索塔，桥塔高度为95.4 m。斜拉索采用竖扇型密索布置，索塔两侧各布置18对索。全桥总体布置情况和主梁标准横截面分别。

2 有限元模型

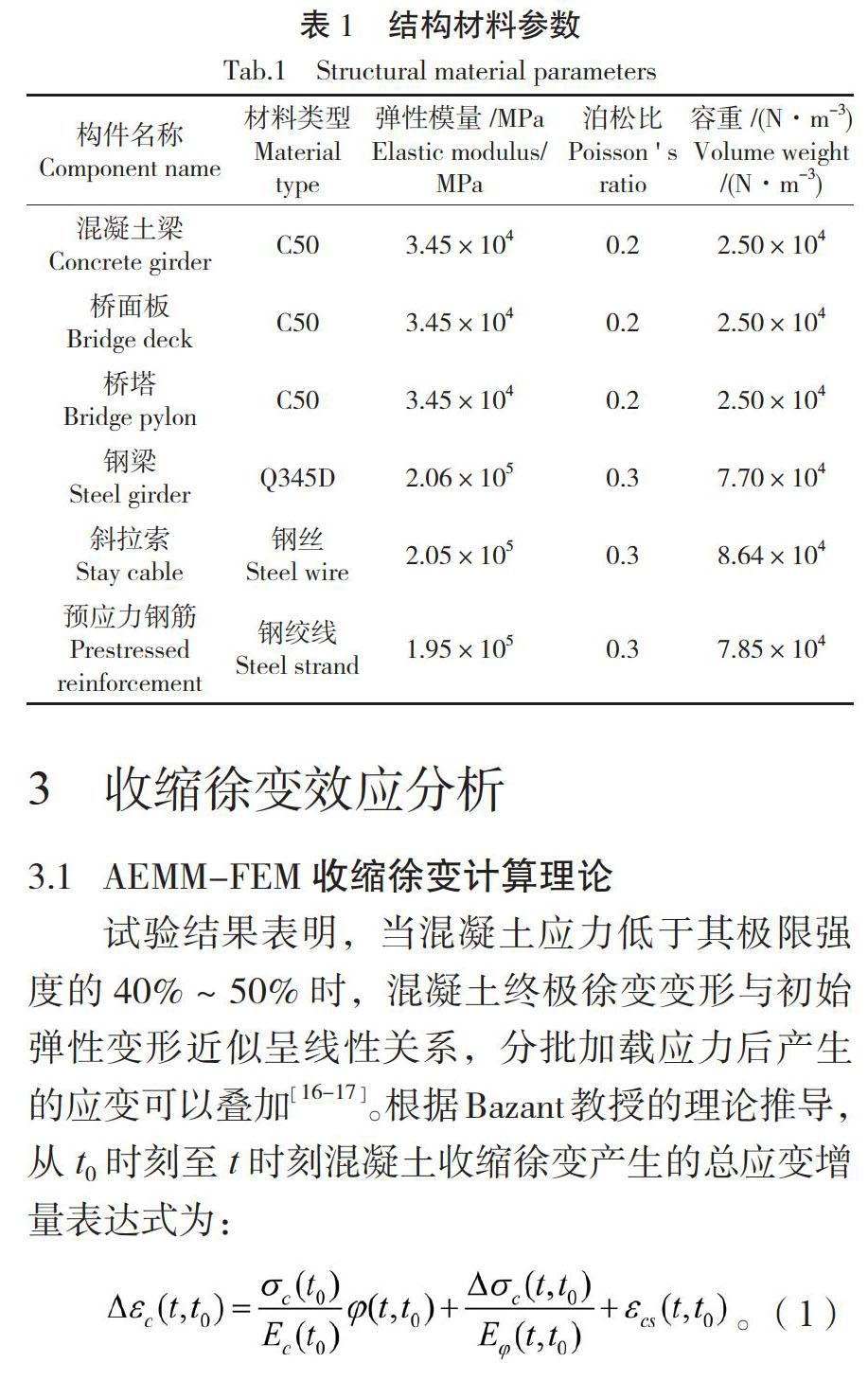
采用Midas/Civil有限元軟件建立全桥空间杆系模型。主梁和桥塔采用梁单元模拟，利用桁架单元模拟斜拉索。桥塔、斜拉索与主梁之间均采用刚性连接，定义节点的边界条件以模拟边墩与辅助墩，对模型施加自重、预应力、拉索力和车辆等荷载。材料参数特性值见表1。

3 收缩徐变效应分析

3.1   AEMM-FEM收缩徐变计算理论

试验结果表明，当混凝土应力低于其极限强度的40% ～ 50%时，混凝土终极徐变变形与初始弹性变形近似呈线性关系，分批加载应力后产生的应变可以叠加[16-17]。根据Bazant教授的理论推导，从t0时刻至t时刻混凝土收缩徐变产生的总应变增量表达式为：

由公式（1）可知，收缩徐变产生的应力增量与应变增量具有线性关系，对收缩徐变问题可以用解弹性结构的方法进行求解。按照实际情况和精度要求将施工过程划分为若干个计算时段，在单个时段内可以利用有限单元法和逐步递推法迭代计算混凝土收缩徐变引起的内力和位移。

3.2 收缩徐变对主梁线形的影响

在有限元模型中采用CEB-FIP1990预测模型反映混凝土材料的收缩徐变性质。除组合梁桥面板预制龄期为180 d外，其余混凝土材料加载龄期均为28 d。全桥混凝土收缩龄期取3 d，环境相对湿度取70%。收缩徐变对混合式钢混组合梁斜拉桥主梁线形的影响，其中成桥初期代表桥梁建成通车的时间。

由于边跨混凝土主梁变形受到辅助墩的限制，其整体竖向变形程度较小。不考虑收缩徐变影响时，混凝土主梁在成桥初期的上挠最大值为13.77 mm。混凝土收缩徐变使主跨钢混组合梁发生下挠变形，组合梁在成桥初期的挠度最大值增加了35.14 mm。随着运营时间的增加，组合梁跨中挠度不断发展，成桥运营15 a后组合梁下挠最大值达108.52 mm，相比成桥初期的组合梁变形，收缩徐变引起的组合梁挠度最大增长率达79.31%。组合梁最大挠度变化趋势为先快后慢，成桥运营前5 a组合梁最大下挠变形占前15 a变形的43.62%，从而可知成桥运营后期组合梁线形变化趋于收敛。施工时应充分考虑混凝土收缩徐变对钢混组合梁线形的影响，对主跨组合梁设置足够大的预拱度来抵消收缩徐变引起的下挠变形。

3.3 收缩徐变参数影响分析

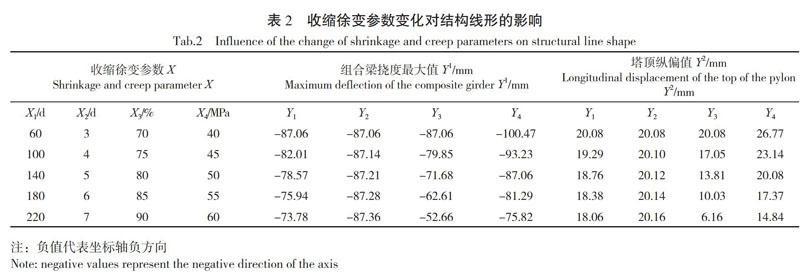
混凝土收缩徐变受材料种类、自然环境和施工工艺等多种因素耦合作用，参考文献[18]，选择桥面板预制龄期X1、混凝土收缩龄期X2、环境相对湿度X3、混凝土抗压强度X4作为参数分析的变量。由于桥塔和主梁采用同种混凝土材料，此处的环境相对湿度、收缩龄期和抗压强度变化适用于全桥所有混凝土构件。在基准模型中，混凝土梁与桥塔的加载龄期均为28 d，X1、X2、X3、X4的取值分别为60 d、3 d、70%和50 MPa，考虑到运营时间会对结构收缩徐变效应产生影响，将基准模型的运营时间统一设置为5 a。改变收缩徐变某一参数值，控制其余参数值不变，收缩徐变参数值变化对钢混组合梁和桥塔线形的影响见表2。

由表2的数据可知，随着环境相对湿度、桥面板预制龄期和混凝土抗压强度的增加，组合梁挠度最大值均呈减小趋势。环境相对湿度从70%增加至90%，组合梁挠度变化量最大值为34.40 mm，变化率达39.52%。混凝土处于湿度较大的环境下，胶凝质点间的吸附水蒸发量减少，同时混凝土的水泥水化反应更加充分，收缩徐变效应得以减轻。混凝土桥面板预制龄期从60 d提高至220 d，组合梁挠度最大减少率为15.25%。施工加载前，混凝土桥面板在自重作用下发生初始收缩徐变。预制龄期越长意味着桥面板能够在加载前完成更多的收缩徐变变形，这在一定程度上压缩了桥面板在使用阶段的收缩徐变发展空间。

桥塔变形方面，提高环境相对湿度、桥面板预制龄期和混凝土抗压强度均能减轻塔顶纵向偏移程度。其中环境相对湿度从70%提高至90%，塔顶纵向偏移值最大减少率为69.33%。这是由于提高环境相对湿度、桥面板预制龄期和混凝土抗压强度后主跨组合梁下挠变形减少，主跨斜拉索内力增幅随之减小，桥塔结构变形有所缓解。

4 收缩徐变灰色关联度分析

4.1 灰色关联度分析方法

灰色关联度分析法在原理上是点集拓扑整体比较与函数对应点远近量度的结合，该方法通过数值计算得到关联度序列，从而比较各参数在系统中的敏感性差异[19]，灰色关联度分析步骤如下：

（1）原始数据矩阵的无量纲化处理：选择需要分析的m种参数，对每种参数取n个不同数值，这些参数值组成自变量比较矩阵，各参数值对应的系统影响值组成因变量参考矩阵。以自变量矩阵为例，对原始数据矩阵元素作均值无量纲化处理：

（2）确定灰色关联差异信息矩阵：对自变量矩阵与因变量矩阵进行差值绝对化计算，根据计算结果建立差异信息矩阵，提取中的最大值M与最小值m，计算关联系数：

（3）计算灰色关联度序列：对于同一自变量的关联系数，取其平均值作为该自变量与系统因变量之间的关联度：

将关联度按数值大小进行排序，关联度越大说明该因素对系统的敏感性越大。同时排序结果与采取的数据处理方法无关，分析结果具有可靠性。

4.2 收缩徐变参数敏感性分析

提取表2中的数据结果，组成自变量比较矩阵[X1k X2k X3k X4k]T和因变量参考矩阵[Y e1k Y e2k Y e3k Y e4k]T（k=1，2，…，5;e=1，2），组合梁挠度、塔顶纵偏的灰色关联差异信息矩阵分别为：

分辨系数取0.5，按照灰色关联度方法进行数值计算，各影响参数与主梁挠度之间的关联度矩阵记为r1，各影响参数与塔顶纵偏值之间的关联度矩阵记为r2，计算结果为：

按数值大小对灰色关联度进行排序，结果为：

由灰色关联度序列可知，混凝土抗压强度是影响主跨钢混组合梁线形的最敏感因素，其次是环境相对湿度和收缩龄期，桥面板预制龄期对组合梁线形的影响最小。混合式钢混组合梁斜拉桥塔顶变形受混凝土收缩龄期的影响最为严重，混凝土抗压强度、桥面板预制龄期和环境相对湿度的影响依次递减。

5 结论

通过对混合式钢混组合梁斜拉桥进行收缩徐变效应分析，得出如下结论：

（1）在收缩徐变的作用下，成桥初期组合梁跨中最大挠度增加了35.14 mm，组合梁下挠变形随着运营时间的增加而不断发展，施工时应设置足够的预拱度以抵消运营期间收缩徐变引起的主梁变形。

（2）组合梁桥面板预制龄期从60 d提高至220 d，组合梁挠度减少率最大值为15.25%。施工时应为混凝土桥面板初始收缩徐变留足时间，从而减轻收缩徐变对组合梁的不利影响。

（3）根据灰色关联度分析结果，混凝土抗压强度是影响组合梁线形的最敏感因素，混凝土强度等级从C40提高至C60，组合梁下挠减少量为24.65 mm。单从此方面来看，设计混合式钢混组合梁斜拉桥设计时，应优先选择强度等级较高的混凝土。

【参 考 文 献】

[1]陶海， 林岩松， 常英. 预应力混凝土箱梁桥的裂缝成因及分析方法 [J]. 森林工程，2004，20（6）：49-50.

TAO H， LIN Y S， CHANG Y. Causes of crack and analysis methods of prestressed concrete box-girder bridge[J]. Forest Engineering， 2004， 20（6）：49-50.

[2]陈亮， 邵长宇. 结合梁斜拉桥混凝土收缩徐变影响规律 [J]. 桥梁建设，2015，45（1）：74-78.

CHEN L， SHAO C Y. Influential laws of concrete shrinkage and creep of composite girder cable-stayed bridge[J]. Bridge Construction， 2015， 45（1）：74-78.

[3]栾兆健， 贾艳敏. 预应力混凝土小箱梁預应力阶段预应力损失分析 [J]. 森林工程，2013，29（6）：120-122.

LUAN Z J， JIA Y M. The analysis of post-tensioned prestressed loss for small box girder[J]. Forest Engineering， 2013， 29（6）：120-122.

[4]BAZANT Z P， BAWEJA S. Justification and refinements of model B3 for concrete creep and shrinkage 1. statistics and sensitivity[J]. Materials & Structures， 1995， 28（7）：415-430.

[5]丁文胜， 吕志涛， 孟少平，等. 混凝土收缩徐变预测模型的分析比较 [J]. 桥梁建设，2004（6）：13-16.

DING W S， LU Z T， MENG S P， et al. Analysis and comparison of prediction models for concrete shrinkage and creep[J]. Bridge Construction， 2004（6）：13-16.

[6]GARA F， RANZI G， LEONI G. Time analysis of composite beams with partial interaction using available modelling techniques： A comparative study[J]. Journal of Constructional Steel Research， 2006， 62（9）：917-930.

[7]ZVOLAINEK L， TERZIJSKI I. Relaxation of structural concrete due to its shrinkage in terms of age-adjusted effective modulus method[J]. Key Engineering Materials， 2017， 737：471-476.

[8]樊健生， 聂鑫， 李全旺. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究（Ⅱ）—理论分析 [J]. 土木工程学报，2009，42（3）：16-22.

FAN J S， NIE X， LI Q W. Long-term behavior of composite beams with shrinkage， creep and cracking （Ⅱ）： theoretical analysis[J]. China Civil Engineering Journal， 2009， 42（3）：16-22.

[9]温庆杰， 叶见曙. 钢-混凝土组合梁的收缩徐变效应分析 [J]. 工业建筑，2006，36（s1）：492-495.

WEN Q J， YE J S. Shrinkage and creep effects of steel-concrete composite beams[J]. Industrial Construction， 2006， 36（s1）：492-495.

[10]RANZI G， BRADFORD M A. Analytical solutions for the time-dependent behavior of composite beams with partial interaction [J]. International Journal of Solids & Structures， 2006， 43（13）：3770-3793.

[11]樊健生， 聂建国， 王浩. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究（I）——试验及计算 [J]. 土木工程学报，2009，42（3）：8-15.

FAN J S， NIE J G， WANG H. Long-term behavior of composite beams with creep， shrinkage and cracking （I）： experiment and calculation[J]. China Civil Engineering Journal， 2009， 42（3）：8-15.

[12]刘沐宇， 李倩， 黄岳斌，等. 港珠澳大桥钢-混组合连续梁桥超长时间收缩徐变效应 [J]. 中国公路学报，2016，29（12）：60-69.

LIU M Y， LI Q， HUANG Y B， et al. Ultra-long time performance of steel-concrete composite continuous beam in Hong Kong-Zhuhai-Macao bridge with creep and shrinkage of concrete slabs[J]. China Journal of Highway and Transport， 2016， 29（12）：60-69.

[13]高翔， 周尚猛， 陈开利. 混合梁斜拉桥钢混结合段试验研究技术新进展 [J]. 钢结构，2015，30（6）：1-4.

GAO X， ZHOU S M， CHEN K L. New development of the experimental research on steel-concrete composite beam cable-stayed bridge[J]. Steel Construction， 2015， 30（6）：1-4.

[14]刘超. 大跨度混合式结合梁斜拉桥地震响应与减震研究 [J]. 武汉：武汉理工大学，2014.

LIU C. Seismic response and shock absorption research of long-span hybrid beam cable-stayed bridge[D]. Wuhan： Wuhan University of Technology， 2014.

[15]QARRA A H. The dee estuary bridge - control of geometry during construction[J]. Proceedings of the Institution of Civil Engineers Civil Engineering， 1999， 132（1）：31-39.

[16]李建慧， 李爱群， 周广盼. 混凝土自锚式悬索桥收缩徐变效应分析 [J]. 防灾减灾工程学报，2016（6）：906-912.

LI J H， LI A Q， ZHOU G P. Shrinkage and creep effects analysis of concrete self-anchored suspension bridge[J]. Journal of Disaster Prevention and Mitigation Engineering， 2016（6）：906-912.

[17]秦煜，劉来君，李青良，等.混凝土桥梁收缩特性影响因素敏感性分析[J].公路工程，2014，39（6）：20-24.

QIN Y， LIU L J， LI Q L， et al. Sensitivity analysis for concrete bridge shrinkage[J]. Highway Engineering， 2014， 39（6）：20-24.

[18]苏成， 陈兆栓， 徐郁峰，等. 预应力混凝土斜拉桥收缩徐变效应的概率分析 [J]. 华南理工大学学报（自然科学版），2012，40（7）：8-14.

SU C， CHEN Z S， XU Y F， et al. Probability analysis of shrinkage and creep effect of prestressed concrete cable-stayed bridges[J]. Journal of South China University of Technology （Natural Science Edition）， 2012， 40（7）：8-14.

[19]陈志波， 简文彬. 边坡稳定性影响因素敏感性灰色关联分析 [J]. 防灾减灾工程学报，2006，26（4）：473-477.

CHEN Z B， JIAN W B. Sensitivity analysis of slopes stability based on grey correlation analysis[J]. Journal of Disaster Prevention and Mitigation Engineering， 2006， 26（4）：473-477.