垂直欠驱动TORA系统的仿真实验

赵海滨，颜世玉，陆志国，刘 冲，于清文

(东北大学 机械工程与自动化学院，沈阳 110819)

0 引 言

具有旋转激励的平移振荡器(Translation Oscillators with Rotating Actuator，TORA)由一个未驱动的小车和驱动的小球组成[1]，来源于双自旋航天器的简化模型。TORA系统是一种典型的欠驱动机械系统，在控制理论的研究中可以作为一个基准系统，用于对不同算法进行验证[2]。最初的TORA系统中，小球是在水平面内转动[3-4]，目前很多学者研究了小球在垂直平面内的转动问题[5-7]。TORA系统的控制方法主要有PD控制方法[8]、反馈控制方法、反步控制方法、基于能量的控制方法[8]和滑模控制方法[9]等。

本文首先对垂直欠驱动TORA系统的动力学方程进行分析，然后建立仿真模型，并采用PD控制器进行控制。在PD控制器中，需要检测小球的角度和角速度。由于获取小球的角速度一般比较困难或者非常昂贵，因此设计了高通滤波器，通过对小球的角度进行高通滤波获取伪角速度。在PD控制器中采用伪角速度代替角速度。最后，通过Matlab/Simulink软件对欠驱动TORA系统建立了仿真实验系统，并进行了数值仿真验证。学生可以修改参数，然后进行动态仿真。通过仿真实验，向学生完整的展示了欠驱动系统的控制过程，能够加深学生对欠驱动系统的理论、仿真和控制等的理解，增强学生的编程能力和学习兴趣，有助于理论和实验教学的结合。

1 垂直欠驱动TORA系统

垂直欠驱动TORA系统由驱动的小球和未驱动的移动小车组成，如图1所示。小车通过弹簧和固定的墙面连接，小车和弹簧在水平面内做一维运动。小球在电机的驱动下在垂直平面内做旋转运动。通过小球的转动和小车位移之间的耦合作用，实现旋转小球对小车的控制。小车的质量为M，位移为x，受到水平面上的摩擦力为f。小球的质量为m，转动半径为r，输入转矩为τ，关于其质心的转动惯量为J，逆时针转离竖直向下方向的角度为θ。弹簧的弹性系数为k，重力加速度为g。

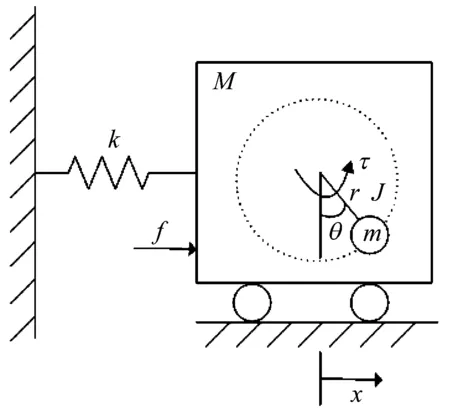
图1 垂直欠驱动TORA系统

TORA系统的总动能包括小车的动能和小球的动能，总动能为

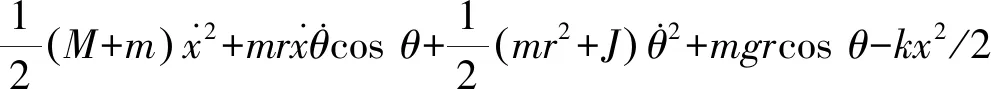
(1)

TORA系统的总势能包括小球的重力势能和弹簧的弹性势能，总势能为

P=-mgrcosθ+kx2/2

(2)

TORA系统的拉格朗日算子函数为

L=K-P

(3)

根据拉格朗日方程[10]，系统的动力学方程为

(4)

最后得到的TORA系统动力学模型为

(5)

TORA系统中有两个状态变量，分别是小车的位移x和小球的角度θ，但只有一个控制输入τ，因此TORA系统是欠驱动机械系统。

2 控制系统

对于欠驱动TORA系统，最常用的控制器为PD控制器。PD控制器和基于能量的控制方法是一致的。采用小球的角度和角速度的PD控制器为

(6)

式中：参数kp>0；kd>0。

在式(6)中，需要检测小球的角度和角速度，对于小球角度的检测比较容易，但是检测角速度一般比较困难或比较昂贵。下面通过设计动态高通滤波器，通过对小球的角度进行高通滤波获取伪角速度。动态滤波器设计为

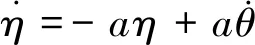
(7)

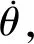
(8)

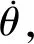
τ=-(kpθ+kdη)

(9)

3 仿真实验

Matlab/Simulink软件在系统仿真和自动控制等领域的研究与教学中应用非常的广泛[11-14]。为了对算法进行验证，本文采用Matlab/Simulink软件建立了仿真实验系统，如图2所示。在图2中，主要采用了Simulink软件中用户自定义函数库中的Matlab Function模块和积分模块[15]等。Matlab Function模块可以采用Matlab语言非常方便灵活的建立复杂系统，非常适合进行动态系统的建模[16]。

TORA系统的参数[5-6]为：小车的质量M=1.260 8 kg，小球的质量m=96 g，半径r=0.592 m，转动惯量J=0.217 5 g·m2，弹簧的弹性系数k=186.3 N/m，重力加速度为g=9.81 m/s2。本文不考虑小车受到水平面的摩擦力，因此f=0。

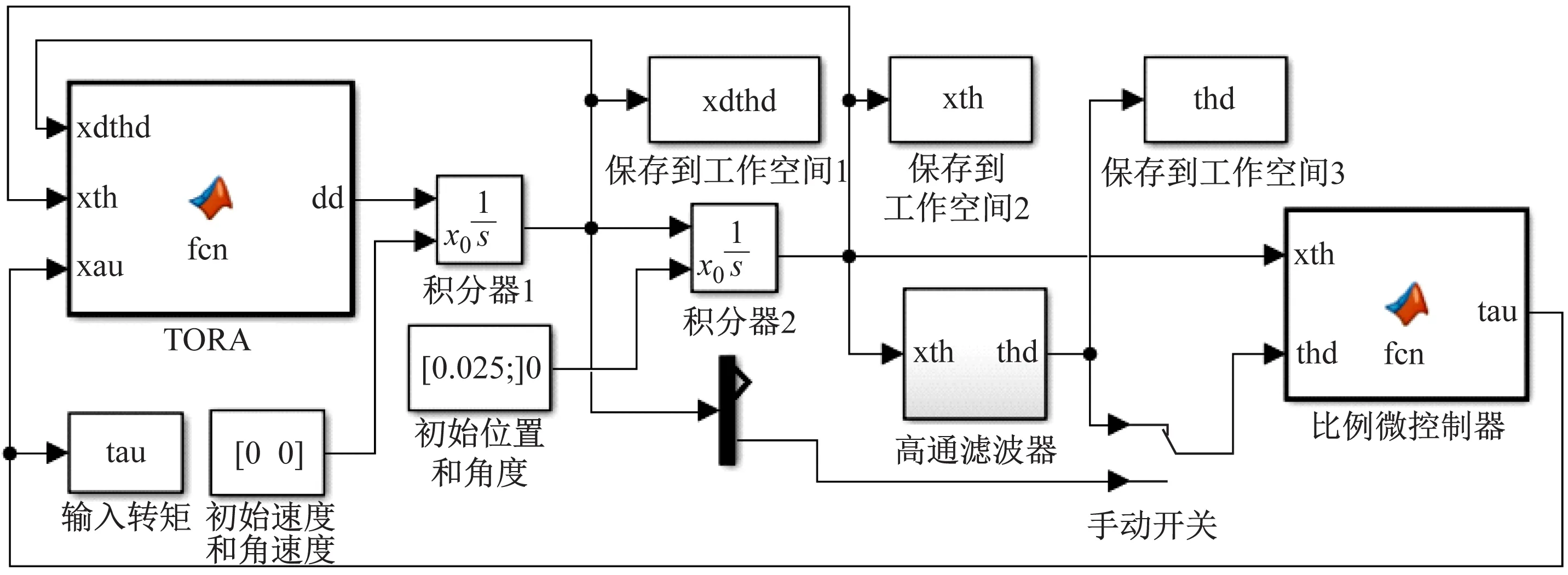
图2 TORA系统的PD控制实验

在图2中，仿真系统采用变步长的ode45算法，最大步长为1 ms，仿真时间为20 s。通过Constant模块设置初始值。通过Manual Switch模块进行小球角速度的选择。通过To Workspace模块将运行结果保存在工作空间中。

根据TORA系统的动力学方程建立仿真模型。在图2中，TORA模块内的代码为

function dd = fcn(xdthd,xth,tau)

M=1.3608;m=0.096;k=186.3;r=0.0592;

J=0.0002175;g=9.81;

x=xth(1);th=xth(2);thd=xdthd(2);

d11=M+m;d12=m*r*cos(th);

d21=d12;d22=m*r^2+J;

D=[d11,d12;d21,d22];

C=[0,-m*r*thd*sin(th);0,0];

g1=k*x;g2=m*g*r*sin(th);

G=[g1;g2];

dd=D([0;tau] - C*xdthd - G);

在图2中，PD模块内的代码为

function tau = fcn(xth,thd)

th=xth(2);

kp=0.012;kd=0.002;

tau=-(kp*th + kd*thd);

根据式(8)，建立子系统模块High-pass filter，如图3所示。图中，高通滤波器的参数设置为a=65。

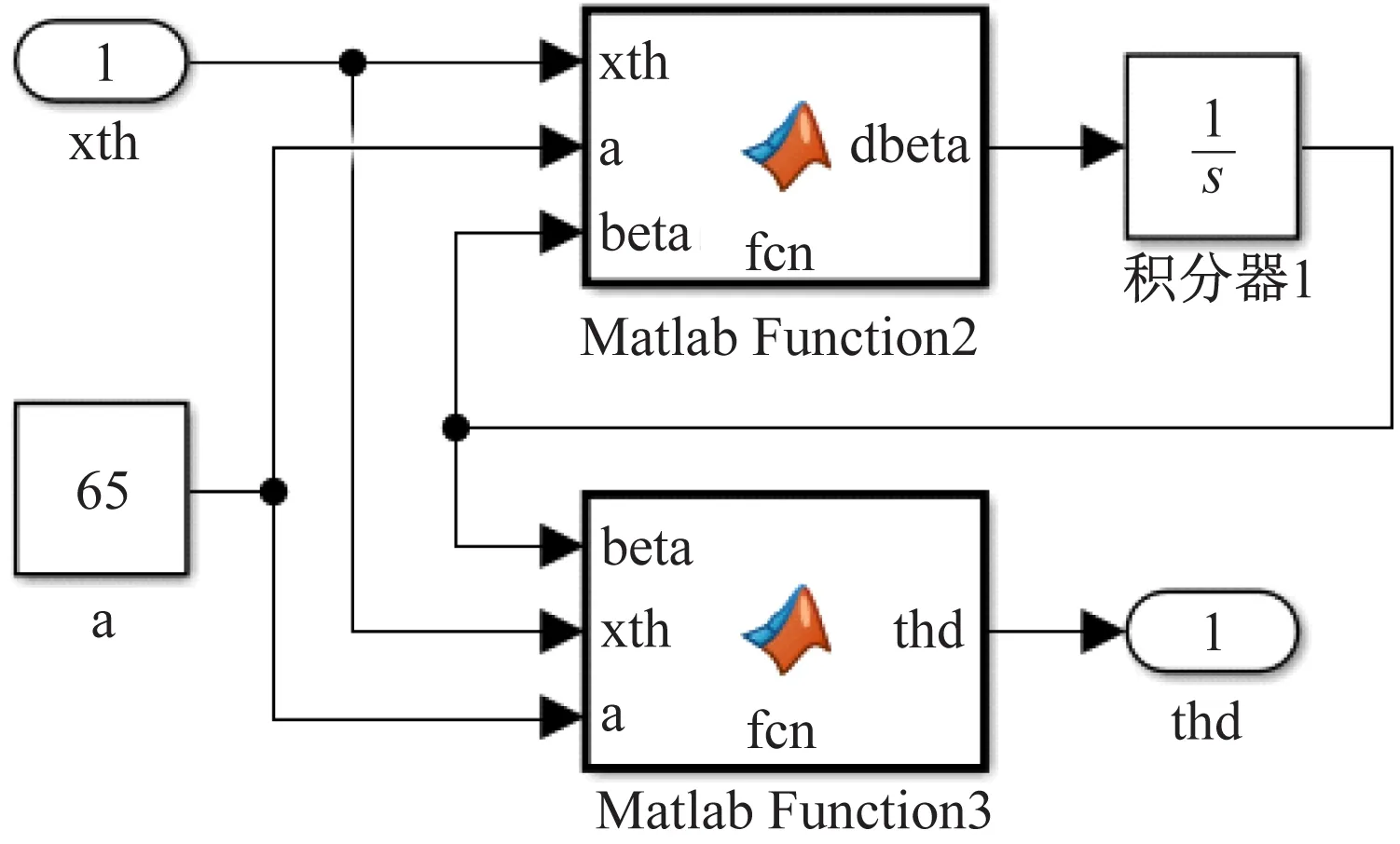
图3 高通滤波子系统

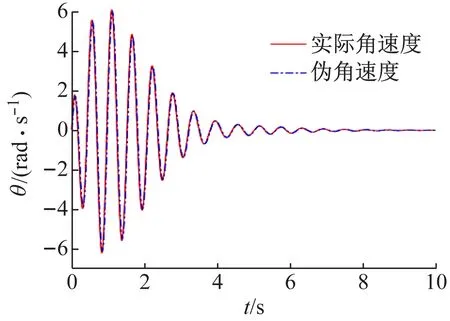
图4 小球的角速度

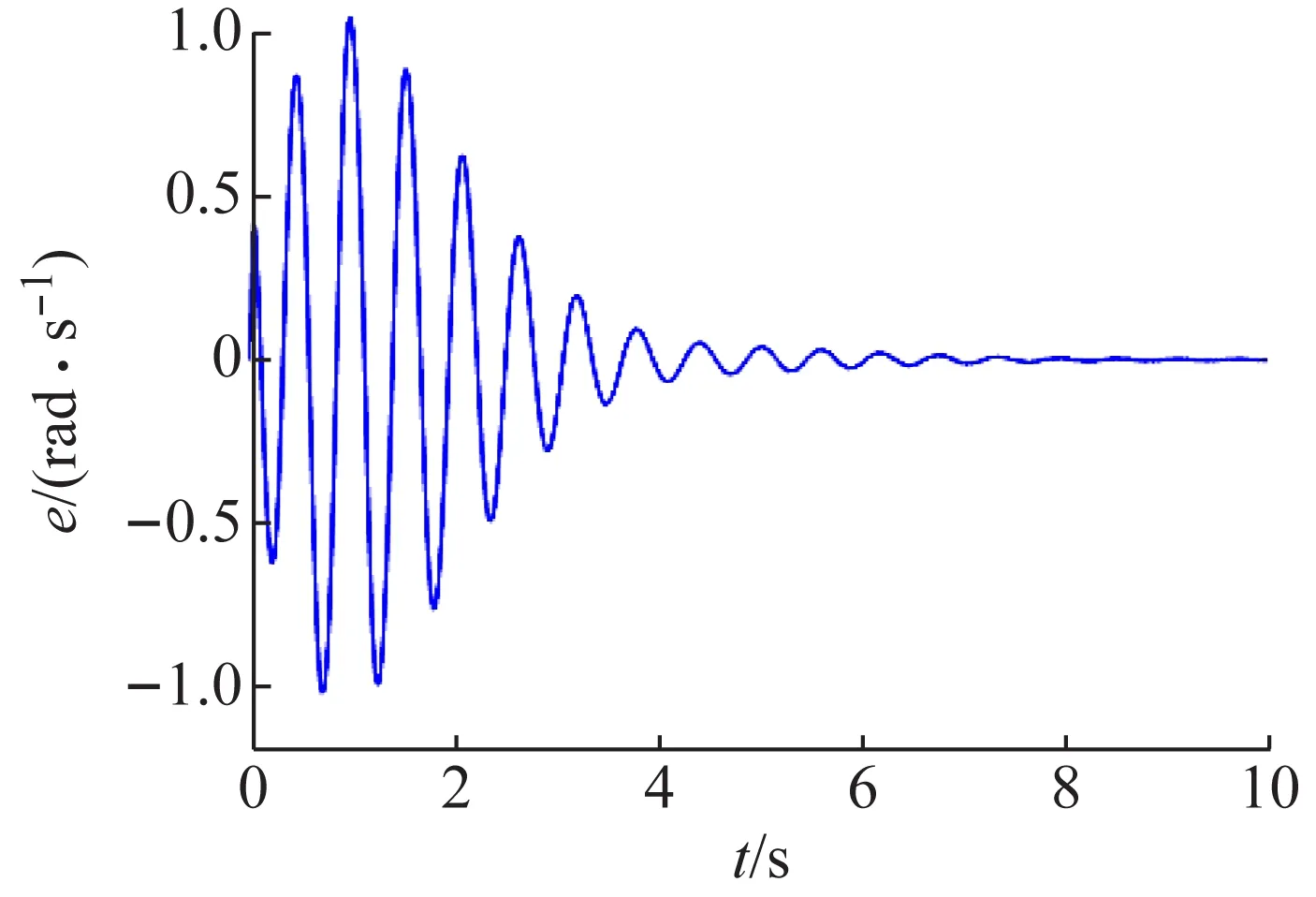
图5 角速度之间的差值

小车的初始位置为x=25 mm，在PD控制器下，小车的位移如图6所示。小车的位移逐渐减小，最终趋近于0。

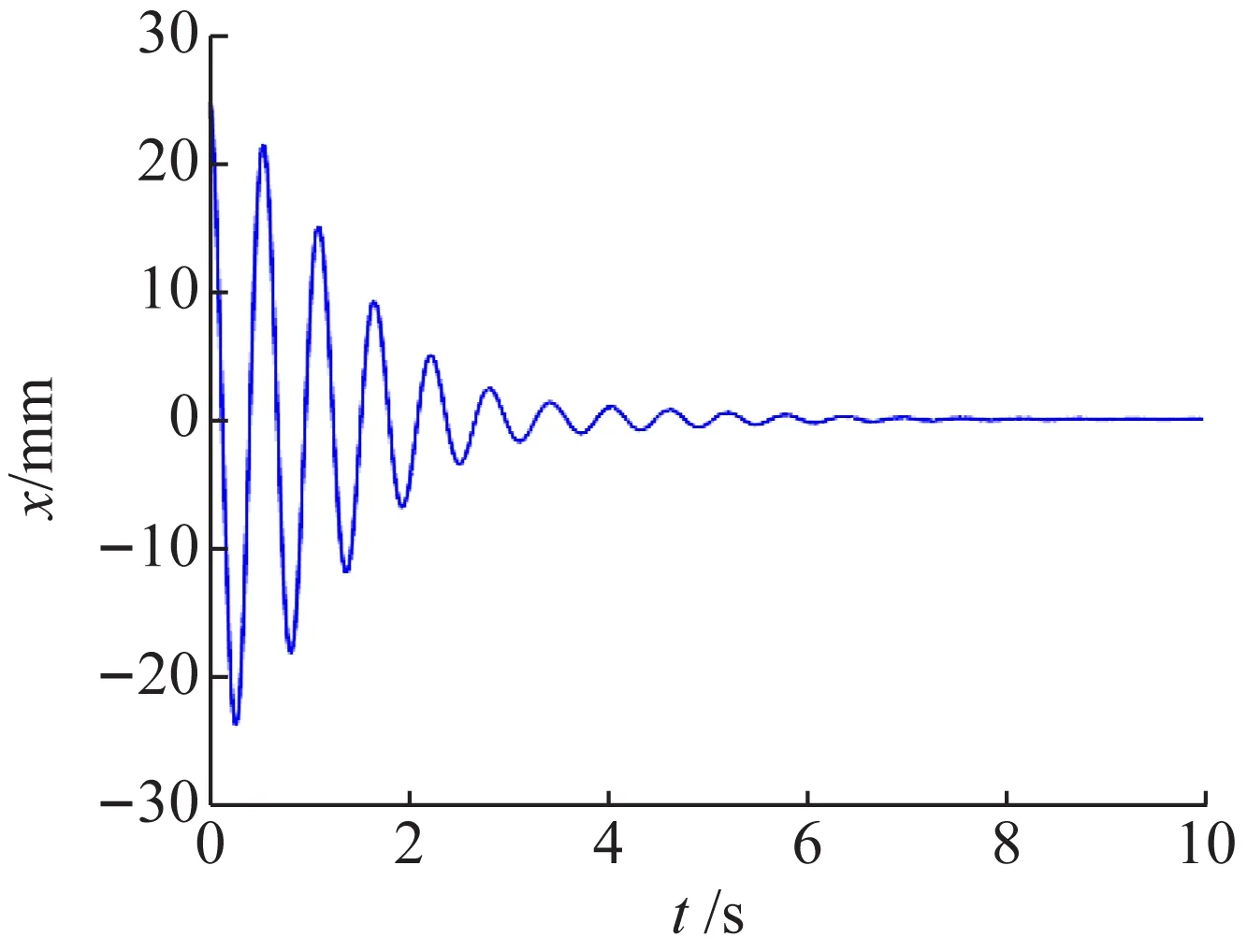
图6 小车的位移

在动力学方程和PD控制器中，小球的角度采用弧度制。将小球的角度转换为(°)后，如图7所示。小球的角度初始值为0。小球角度的最大值为30.30°，最小值为-31.47°，最终逐渐趋近于0。

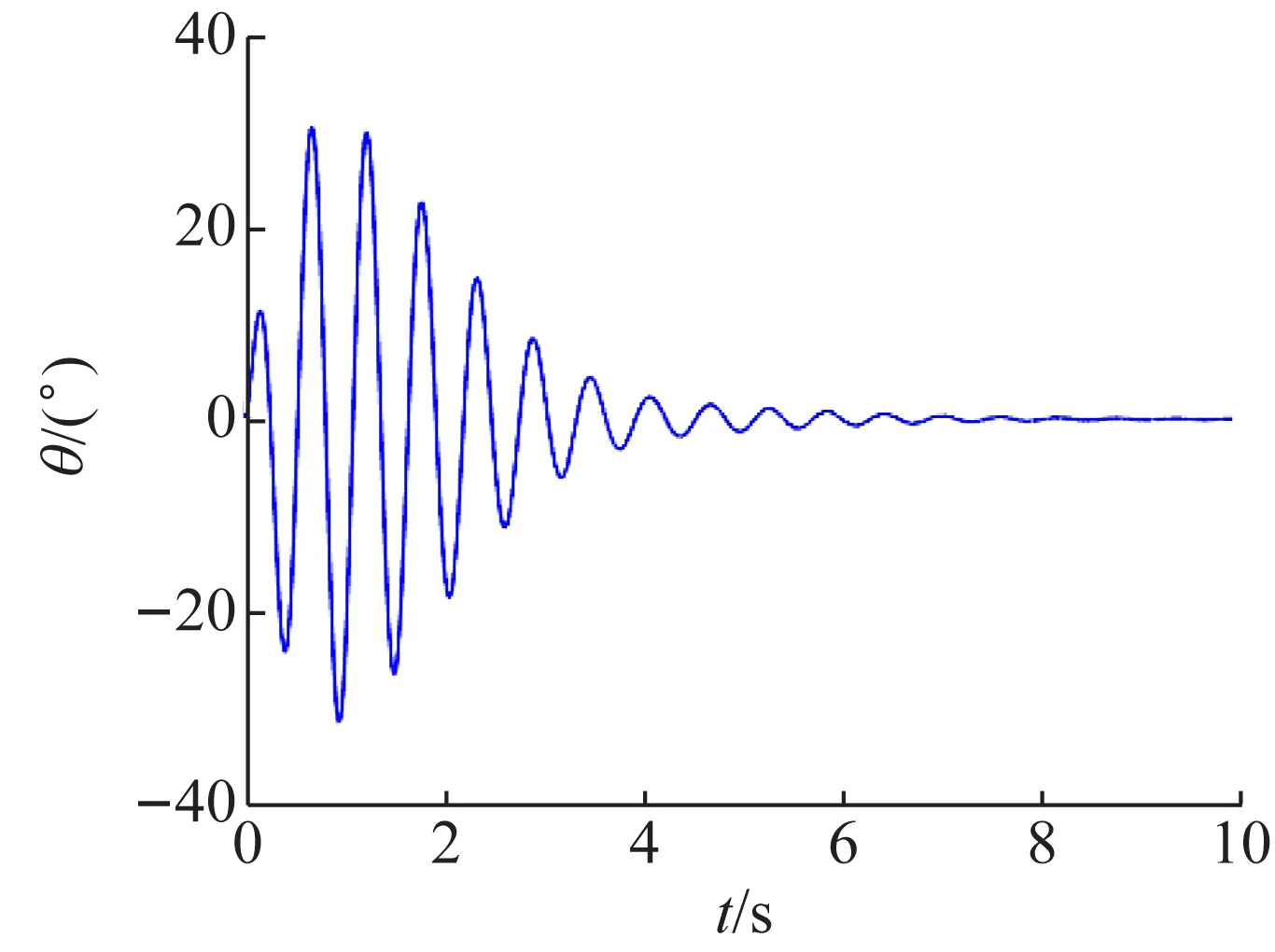
图7 小球的角度

小球的驱动力矩如图8所示。在图8中，驱动力矩的初始值为0，最大值为14.9 mN·m，最小值为-14.4 mN·m。驱动力矩逐渐减小，并趋近于0。

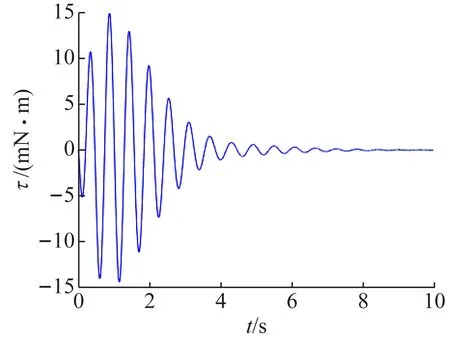
图8 驱动力矩

4 结 语

根据垂直欠驱动TORA系统的动力学方程，建立仿真模型，并采用PD控制器进行控制。通过Matlab/Simulink软件建立了仿真和控制实验系统。设计了高通滤波器，对小球的角度进行高通滤波后得到伪角速度。在PD控制器中，采用伪角速度代替实际的角速度。实验结果表明，能够进行TORA系统的平衡控制。通过仿真实验，学生可以对TORA系统的仿真和控制系统有一个完整的了解，还可以自己修改系统的参数或编写控制算法。该仿真实验能够加深学生对欠驱动系统的理论、仿真和控制等的理解，增强学生的实际编程能力和学习兴趣，培养学生的创新意识和能力。