基于区间数的黄金湿法冶炼过程建模与优化研究

刘亚东 牛大鹏 常玉清 王福利 张永京

黄金湿法冶炼生产过程的优化控制是实现过程精细化操作、提高综合生产指标的有效途径.下文将黄金湿法冶炼简称为湿法冶金.建立湿法冶金过程优化控制系统可以最大限度地提高产量、精矿品位、黄金回收率、矿产资源的综合利用率等技术经济指标,达到高产优质、节能降耗等目的,对最终提高企业经济效益、解决我国有色金属资源枯竭和可利用矿物资源多为低品位矿和复杂矿等资源问题具有极为重要的意义[1−2].

目前对湿法冶金过程的优化控制多是基于定量数学模型.马恩杰等利用物料衡算关系建立了选矿过程的精矿产量、精矿品位和全选比等综合生产指标的机理模型[3].Ding等利用实际过程积累的大量数据,建立了选矿过程精矿品位的数据模型[4].Yu等为了实现对选矿过程综合生产指标的优化,通过物料平衡关系,建立了以原矿处理量为决策变量、以各个综合生产指标上下限、设备能力、能源上限、尾矿品位限制以及原矿处理量上下限为约束条件的选矿优化模型,并利用改进的遗传算法完成了对优化模型的求解[5].de Andrade等根据浸出过程的机理,利用实验数据建立了金湿法冶金浸出过程的静态机理模型,通过该机理模型对浸出过程经济效益进行优化操作[6].Yuan等根据某黄金精炼厂的黄金湿法冶炼工艺,建立了黄金湿法冶炼全流程机理模型[7].

然而,在实际工业生产过程中,由于测量仪表、原料成分、生产工艺及复杂的现场环境等限制,基于过程机理所建立的定量数学模型不可避免地存在着不确定性,例如:参数计算和测量误差;系统在不同工况下,参数具有不同数值;参数具有一定的变化区域无法精确测量等[8−10].由于不确定性因素存在,致使生产过程某些局部环节的模型无法获得,此时也就无法基于过程模型进行优化控制.

近年来一些学者对不确定性的优化方法进行了相关研究,Zhang等[11]针对模型参数不确定性、结构不确定性等模型失配问题,提出一种金氰化浸出过程的修正项自适应实时优化策略,通过利用实际过程测量值及梯度信息不断修正原优化问题,使其迭代收敛到实际过程的最优设定点.Pishvaee等[12]研究了基于模糊可能性规划,进行不确定性条件下封闭供应链网络的设计.Wang等[13]在能够以固定频率对结构件的数据进行测量的情况下,提出了基于区间分析的结构检测技术.Ma等[14]利用区间对一些不确定性因素进行包含的处理,将转子动态响应描述成有边界的不确定性参数.

综上所述,本文针对湿法冶金过程中某些关键变量不能准确在线测量,导致局部环节无法定量建模的问题,提出一种利用专家领域知识和现场操作人员的经验知识等信息建立该环节的模糊定性模型,进而得到在不同的工况条件下,该局部环节的不同定性输出值.在湿法冶金全流程生产过程中,工序之间的复杂关联关系使得全流程优化问题变得极为复杂,导致其求解效率与全局收敛性较低.为此,本文采用文献[15]提出的一种分层优化方法,利用最小消耗模型描述各工序指标相关关系,实现在过程层操作变量未知情况下工序指标的优化,并保证下游流程分层决策结构中获得的工序指标的可行性与最优性.由于模糊定性模型的输出形式为定性值,这使得优化模型存在不确定性,进而无法实现优化求解.而通过现场操作人员的经验知识可以得到该定性值变量参数的大致边界区间.为此,本文提出一种基于区间数的优化方法,利用区间可能度的不确定约束转换模型,使区间不确定约束在某一可能度水平下得以满足,进而将不确定优化模型转化为确定性优化模型.最终通过对定性模型的每一输出模态对下游子流程进行优化操作并构建最优模式库,并在此基础上对全流程实现优化,通过仿真应用证明了本文提出方法的有效性.

1 湿法冶金生产过程

湿法冶金工艺流程复杂,通常由磨矿、浮选、压滤脱水、调浆、浸出、洗涤、置换等众多工序构成,且设备类型多样,整个流程具有多变量、变量之间强耦合等综合复杂性,其生产指标容易受原料成分、工况、设备状态等多种不确定性因素干扰.湿法冶金工艺基本操作流程如图1所示.其中,调浆过程是湿法冶金过程的重要工艺之一,其生产过程和产品质量的稳定对于湿法冶金工艺至关重要.由于生产条件的限制,现场中的矿浆浓度等关键性检测数据不能够直接由仪器准确在线测量,同时,其生产过程中存在非线性、大滞后、干扰因素多等问题,使得调浆过程这一局部环节无法建立准确机理模型,进而无法基于定量模型实现湿法冶金流程过程优化控制.

图1 湿法冶金工艺基本单元操作流程Fig.1 Basic unit operations of hydrometallurgy process

调浆过程其上游工序的矿浆首先进入立式压滤机进行脱水后,滤饼进入矿浆搅拌槽与调浆水进行混合,混合后的矿浆由排矿泵送入到后续的氰化浸出流程的浸出槽中.一次浸出与二次浸出过程各由4个浸出槽组成,其中第1、2和4槽通过添加氰化钠与混合后的矿浆发生浸出反应,实现精矿中的金和杂质的分离,如图2金氰化浸出过程示意图所示.一次浸出和二次浸出后的矿浆通入压滤机中,用置换工序流出的贫液对压滤成的滤饼进行洗涤.之后,一次压滤和二次压滤的滤液作为贵液,送入板框压滤机中与锌粉发生置换反应,生成金泥,最终实现对矿石中金的分离和富集.

图3(a)为压滤机多次工作时的进出料时间,从图中可以看出压滤机每次放矿时间间隔和时间长短都不固定.当放矿量不确定且无法准确测量时,很难通过调浆水的调节使得矿浆浓度稳定,因此进入浸出过程的矿浆浓度波动较大.图3(b)反应了进入浸出槽的矿浆浓度的变化.可以看出由于调浆水量不能根据放矿量的变化进行及时调整,导致浸出槽矿浆浓度大范围波动.而矿浆浓度对金的氰化浸出影响很大,会直接影响金的溶解速度.如图4所示,在其他工况条件保持不变的情况下,矿浆浓度从2%

逐渐增加到90%,随着矿浆浓度的增大,矿浆中固体矿石含量增大,矿石与氰化钠接触面积变大,金的浸出速度变大,浸出率增大.但随着矿浆浓度的继续增加,浸出率增大速度变缓,因为较大的矿浆浓度会使矿浆黏度增高,影响溶液中氰化物和氧的扩散速度,或者因为添加到浸出槽中氰化钠量不够,不足以完全溶解矿石中过多的金,使金溶解速度降低,从而影响金的浸出效果.而浸出率是浸出过程最重要的工艺指标,浸出过程运行性能的优劣直接决定了后续各子流程的实际操作,因而对最终的金回收率产生重要影响[16−17].因此,需要保持浸出槽内矿浆浓度的稳定以获得湿法冶金过程的最大经济效益.

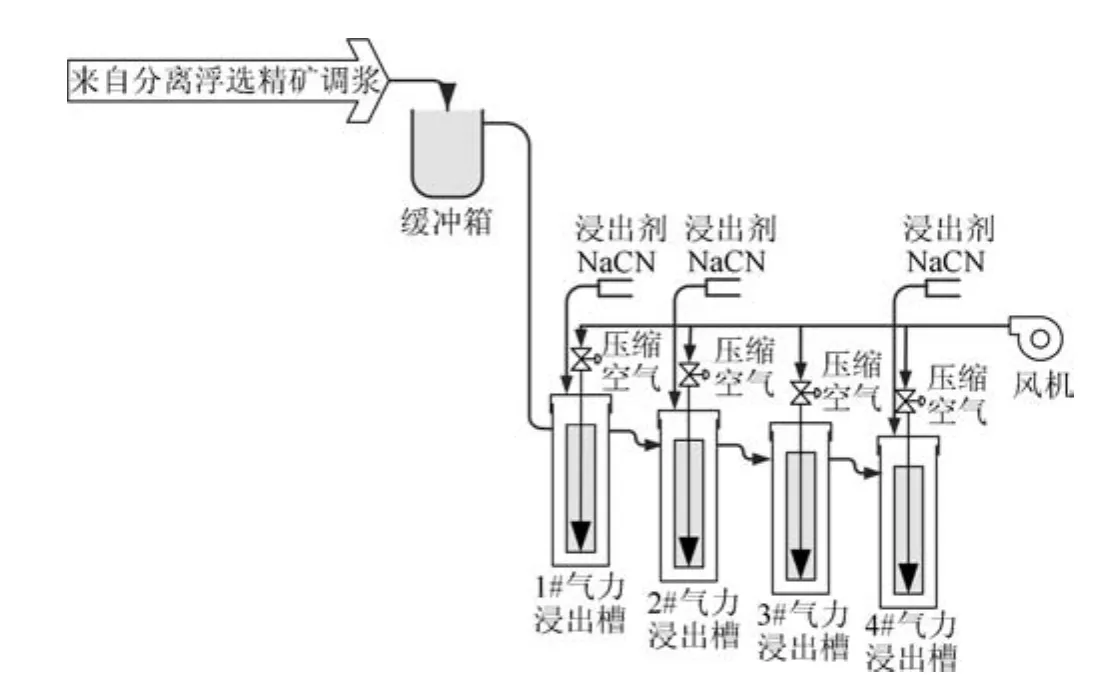
图2 金氰化浸出过程原理示意图Fig.2 Schematic diagram of gold cyanidation leaching

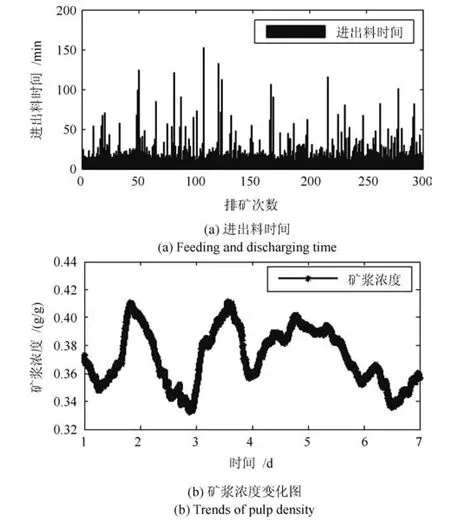
图3 脱水调浆变量变化图Fig.3 Variable variation of dehydration mixing

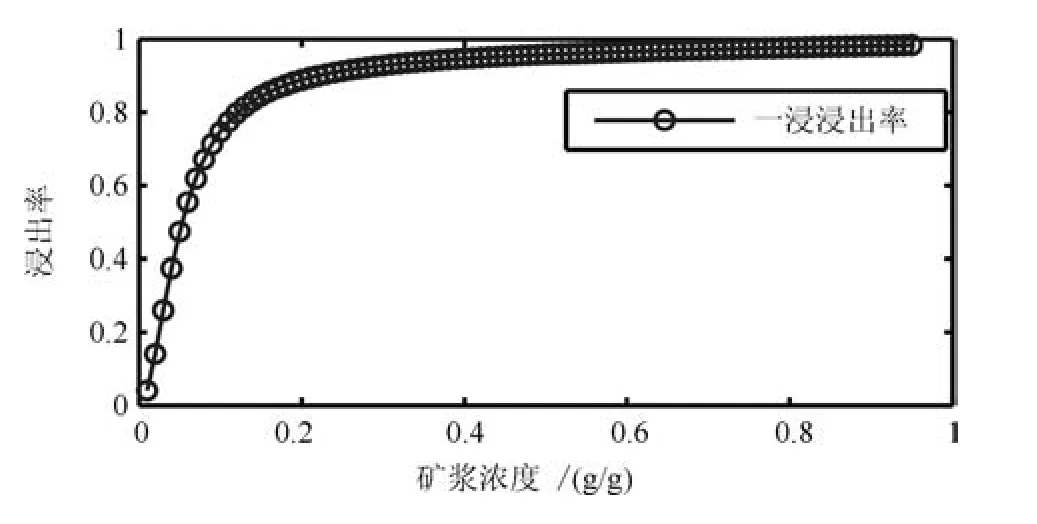
图4 浸出率随矿浆浓度变化图Fig.4 Trends of the leaching rate changing with pulp density

为了获得湿法冶金过程最大经济效益,需要对湿法冶金过程进行建模并优化求解,而矿浆浓度的不确定性使得建模变得困难,为此,本文将矿浆浓度变量用区间数的形式表示其不确定性,通过采用区间优化方法使得过程优化模型建立得以实现,进而求出湿法冶金过程的最大经济效益.不失一般性,本文将湿法冶金调浆过程及其下游子流程合并一起统称为全流程.

2 湿法冶金生产过程

放矿量的不确定性与矿浆浓度的不确定性使得调浆过程无法建立定量模型,这给基于模型的优化方法实现湿法冶金过程优化求解带来了很大的困难.针对这个问题,本文提出了如图5所示的由专家知识模糊定性模型、下游基于区间数的分层优化模型和全流程优化模型组成的基于知识的湿法冶金过程优化框架.首先,针对调浆过程无法建立定量模型问题,提出一种结合专家知识的定性建模方法.然后,针对该定性模型的每一种输出状态,对下游子流程采用基于区间数的分层优化方法求得不同输出状态下的最优经济指标,并构建最优模式库.最后,在下游最优模式库基础上对湿法冶金全流程优化求解,求得在当前输入条件下全流程综合经济效益和与之对应的各个工序的操作条件,建立全流程优化操作模式库.

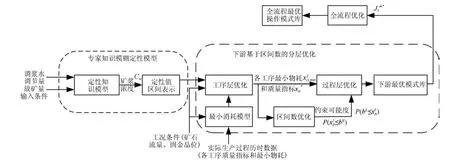
图5 基于知识的湿法冶金过程优化框架Fig.5 Frame of process optimization based on knowledge for hydrometallurgy

2.1 定性知识模型建立

由于无法通过定量模型来描述调浆过程的动态特性,在当前放矿量输入条件下,无法合理地通过调浆水的调节使得矿浆浓度达到稳定值,而矿浆浓度的波动会对后续流程优化操作产生影响,因此,这就给湿法冶金全流程优化带来了很大的障碍.针对这个问题,本文提出一种定量模型与专家知识定性模型相混合的全流程优化方法.

1)调浆过程变量的定性状态划分

由于调浆过程入口条件放矿量不稳定,且不可在线测量,从第1节图2(a)压滤机进出料时间中可以看出,单位时间内压滤机放矿量的大小是不均匀的.针对放矿量的不确定性,本文结合专家经验将输入变量(放矿量∆M)划分为5个状态,分别为负大(NB)、负小(NS)、零(ZE)、正小(PS)、正大(PB),放矿量的状态根据专家经验判断获得.

在实际应用中当调浆水不变时,放矿量的不同将会直接引起矿浆浓度的变化,进而影响后续浸出工序的操作.而对于操作变量调浆水量∆q,现场工人经验只知道当放矿量大时,需加大调浆水;当放矿量小时,需减少调浆水.这种调节方式使得矿浆浓度的发生剧烈波动,且当加大调浆水时造成水资源过度浪费.为此,针对操作变量调浆水量∆q的变化,本文结合专家知识和现场工人经验将操作变量(调浆水量∆q)合理划分为7个状态,分别为负大(NB)、负中(NM)、负小 (NS)、零(ZE)、正小(PS)、正中(PM)、正大(PB),调浆水的状态根据调浆水量测量值的模糊化处理获得.

调浆过程出口条件矿浆浓度Cw也不可在线测量,通常只能根据现场操作人员经验或专家知识估计其所处范围区间[Cwmin,Cwmax].在实际生产过程中,在放矿量变化的情况下,通过不同的调浆水调节得到的矿浆浓度由现场操作人员多次离线化验,可以得到不同等级下矿浆浓度的具体数值.然而,由于实际环境变化和一些干扰因素,使得离线测得数值不准确.为此,针对矿浆浓度的不确定性,本文结合专家知识和现场操作人员经验将输出变量(矿浆浓度Cw)划分为5个状态,分别为负大(NB)、负小(NS)、零(ZE)、正小(PS)、正大(PB),矿浆浓度的状态根据矿浆浓度化验值的模糊化处理获得.

本文采用文献[18]隶属度函数选择方法,确定输出变量矿浆浓度Cw和操作变量调浆水∆q的隶属度函数为三角形隶属函数,如图6所示.这样,通过隶属函数的表达形式将调浆过程变量(矿浆浓度和调浆水调节量)定性划分.

2)调浆过程定性模型

根据调浆过程的工艺特点,利用过程数据及专家知识,采用基于“IFh前提iTHENh结论i”的规则推理结构建立了调浆过程中放矿量、调浆水与矿浆浓度之间的定性关系.

例如:如果当前工况放矿量是正大且操作变量调浆水的偏差为正小,则输出变量矿浆浓度为正小.

以此类推,采用文献[19]的方法,对利用过程数据及专家知识得到的模糊规则进行仿真与实验研究,得到了不同放矿量输入条件下,调浆水量的变化对矿浆浓度的影响规律,进而设计Mamdani模型的调浆过程矿浆浓度模糊规则表,如表1所示.

2.2 下游优化模型求解

实际生产中,在一定的输入条件下,不同操作参数的生产效益差异很大.为此,考虑矿浆浓度对后续工序经济指标的影响,对调浆过程定性知识模型的每一个输出模态(矿浆浓度),对下游子流程建立定量模型,并优化求解.根据在不同模态下求得的综合经济指标,得到不同模态下的最优操作策略(浸出率、置换率、氰化钠添加量、锌粉添加量等),从而建立下游子流程最优模态库.

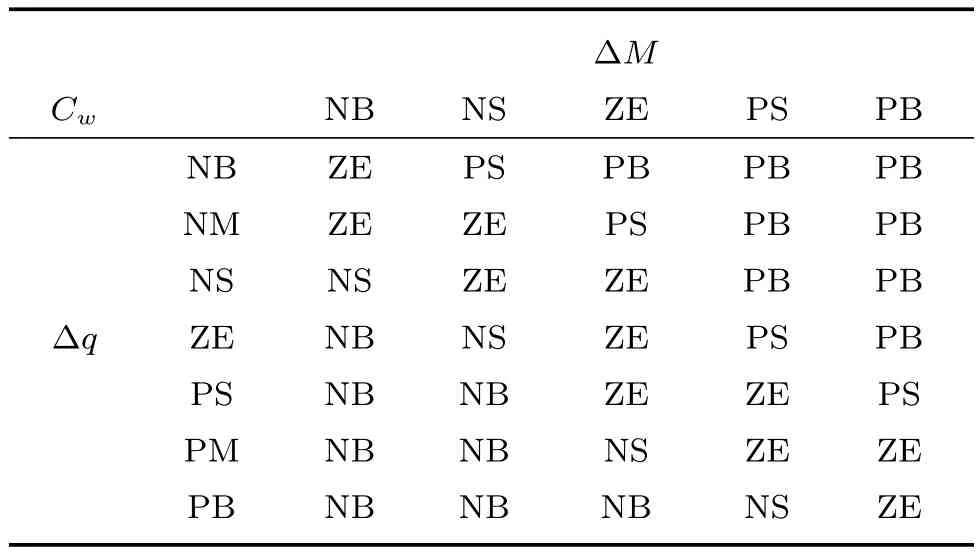
表1 调浆过程矿浆浓度模糊规则Table 1 The fuzzy rules for the pulp density of mixing process

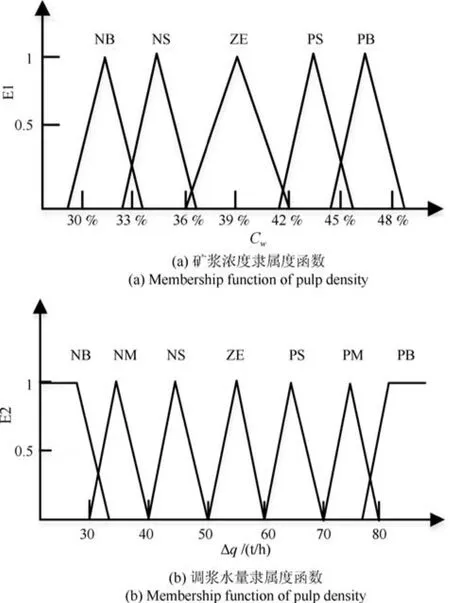
图6 矿浆浓度E1与调浆水E2的隶属度函数Fig.6 Membership functions of pulp density E1 and mixing water E2

2.2.1 决策变量选取

浸出过程中对浸出率影响较大的操作变量是氰化钠添加量,置换过程中对置换率影响较大的操作变量是锌粉添加量.所以,下游子流程优化的决策变量选取为6个浸出槽的氰化钠添加量和置换过程的锌粉添加量.

2.2.2 目标函数

在下游子流程中,将单位时间每小时的经济效益最大作为优化目标.根据下游子流程工艺分析,下游子流程目标函数表示如下:

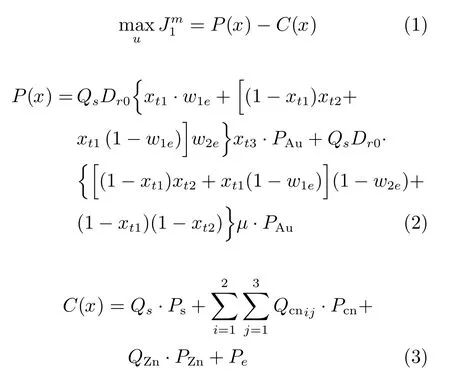
2.2.3 约束

2.2.3.1 物耗与工艺指标之间的关系约束

在湿法冶金流程生产过程中,由于很难建立物耗与各个工序指标之间的机理模型,本文采用文献[15]的方法,运用三层BP神经网络建立物耗与工序指标之间的数据模型.

在压滤洗涤工序中由于只有矿浆浓度对洗涤工序的质量指标洗涤率有影响,且在实际应用中只要矿浆浓度在合适的范围内,洗涤率可以保证在99%以上.所以,本文将洗涤工序指标(一次压滤洗涤率w1e和二次压滤洗涤率w2e)看作常数,即w1e=w2e=99%.

首先,在不同矿浆浓度(离线获得化验值)下,根据不同的工况条件θ(矿石流量、矿的初始固金品位等)从实际生产过程历史数据中收集各工序相关质量指标xt1、xt2和xt3,以及相应的最小物耗xcimin(i=1,2,3)数据,构成建模数据集;然后,将矿浆浓度化验值转化成定性模态m.矿浆浓度的模糊化使得针对每一种矿浆模态,相同工序指标及工况条件的最小物耗值不唯一.针对这个问题,本文采用区间变量表示最小物耗值.综上,针对不同矿浆浓度模态m,以工况条件θ(矿石流量、矿的初始固金品位等)和工序质量指标为输入,以当前模态m下各工序的区间型最小物耗为输出,建立如式(4)所示的基于神经网络的各个工序区间型最小物耗预测模型.

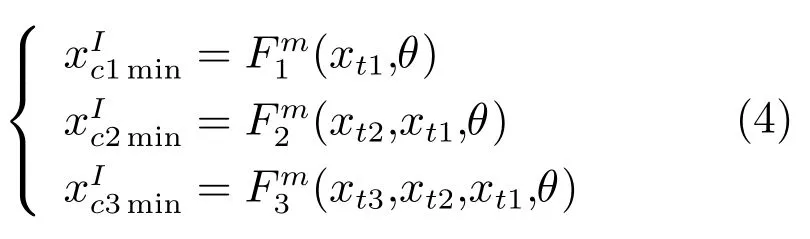
2.2.3.2 生产能力约束

根据流程工艺生产要求,浸出率、置换率和物耗需满足:

其中,g1(xt1,xt2)≤0为总浸出率约束,其表达式为:g1=0.99−xt1−(1−xt1)·xt2≤0;g2(xt3)≤0为置换率约束,其表达式为:g2=0.995−xt3≤0;xci≤xci,max为物耗约束,为一浸和二浸各浸出槽的物耗之和,为浸出过程中第1、2、4这三个浸出槽的氰化钠添加量;为置换过程中锌粉添加量,xc3=QZn;xti,min≤xti≤xti,max,(i=1,2)分别为一浸浸出率、二浸浸出率约束.

2.2.4 下游流程优化模型求解

在实际工业应用中,工序之间的复杂关联关系使得全流程优化问题变得极为复杂,进而导致其求解效率与全局收敛性较低.为此本文采用文献[15]的分层优化方法,利用最小消耗模型描述各工序指标相关关系,进而实现在过程层操作变量未知情况下工序指标的优化,并保证下游流程分层决策结构中获得的工序指标的可行性与最优性.通过前文对湿法冶金流程工艺描述可以看出,其生产流程存在不确定优化问题,这种不确定性表现在变量参数的不确定,即前文提到的矿浆浓度不确定,只知道大致边界.所以针对该问题,本文采用文献[20]的方法,利用区间可能度的不确定约束转换模型,使区间不确定约束在某一可能度水平下得以满足,进而将不确定优化模型转化为确定性优化模型.通过区间数优化方法转化后的确定性优化问题存在两层嵌套优化问题,其中外层优化用于决策变量的寻优,而内层优化用于计算不确定约束的区间.所以,针对该复杂约束的优化问题,本文采用文献[21]的算法实现外层优化和内层优化,从而获得下游全流程综合经济指标.

2.2.4.1 分层优化

分层优化方法将下游流程优化分为工序指标优化与在工序指标优化基础上的过程操作变量优化,实现了下游流程优化问题的分层决策.

该方法所面临的问题是当进行工序指标优化时,过程层操作变量是未知的,而操作变量直接决定工序指标.因此,通过采用最小消耗模型,即第2.2.3.1节中物耗与工序指标之间的关系约束,来描述各工序质量指标之间的相互关系,从而将湿法冶金下游流程优化问题分解为工序层优化和过程层优化两层子优化问题.两层优化问题的具体描述如下:工序层优化模型为

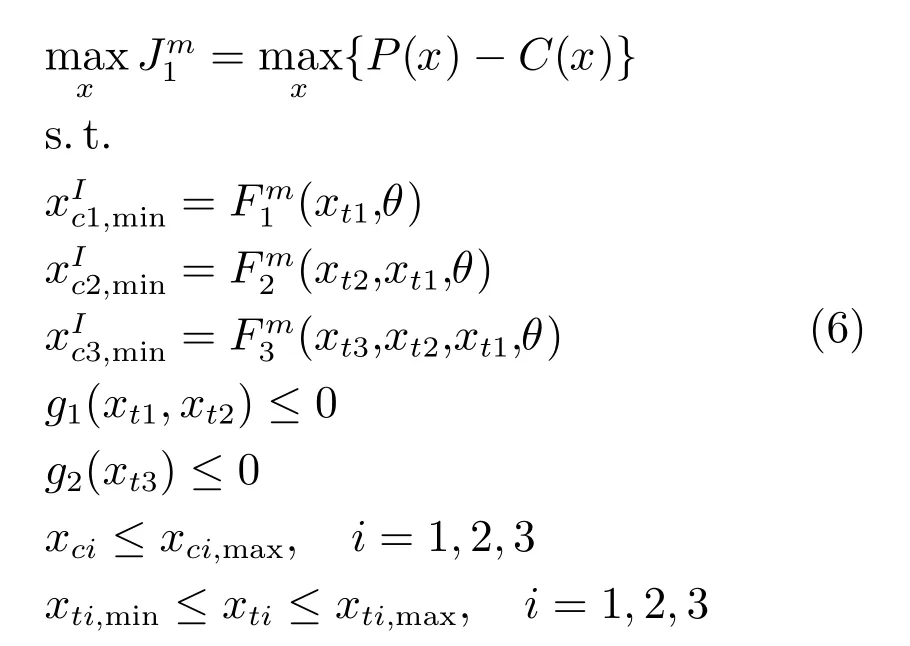
其中,决策向量x包括一浸、二浸和置换过程中的最小物耗区间值(i=1,2,3)和各个工序的质量指标xti(i=1,2,3).

在过程层优化中,要分别对一次浸出、二次浸出以及置换工序进行优化.

一次浸出、二次浸出工序过程层优化模型为

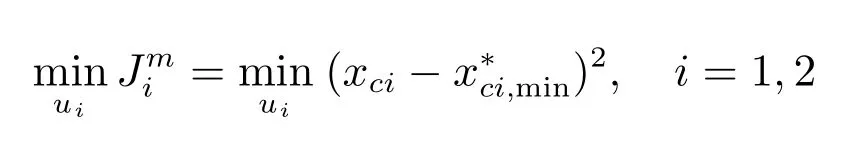
置换工序过程层优化模型为

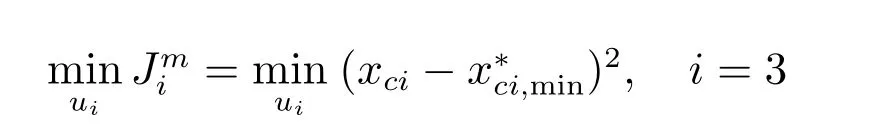
s.t.

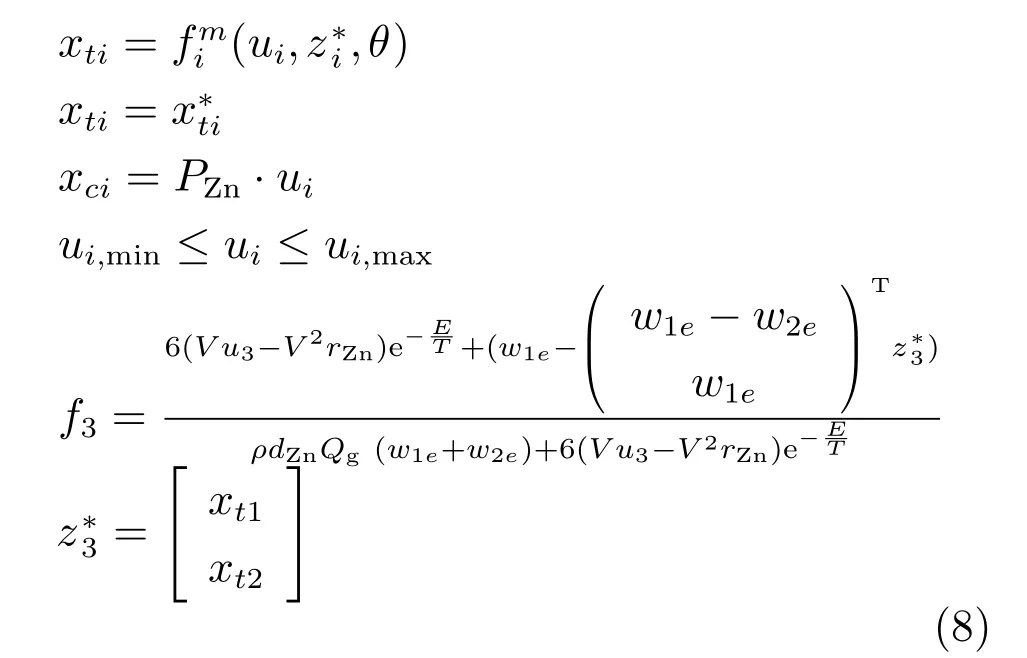
2.2.4.2 区间数优化

实际工业生产中由于矿浆浓度的不确定性,使得与之相关的浸出率受到影响,对于过程层优化模型(7)中的等式约束为一区间型变量,目标值是由工序层优化求得的数值型变量.为此,将原等式约束转化为不等式约束,其中,.对于该不等式约束,由于不确定变量Cw存在,使得不等式约束无法通过常规优化求解,因此采用区间数的优化方法,将原不确定变量等式约束转化为确定性不等式约束,从而实现优化求解.

区间数优化中定义区间可能度用于定量描述一区间大于(或优于)另一区间的程度,针对区间的不同位置关系,应用概率方法,区间可能度构造如下:

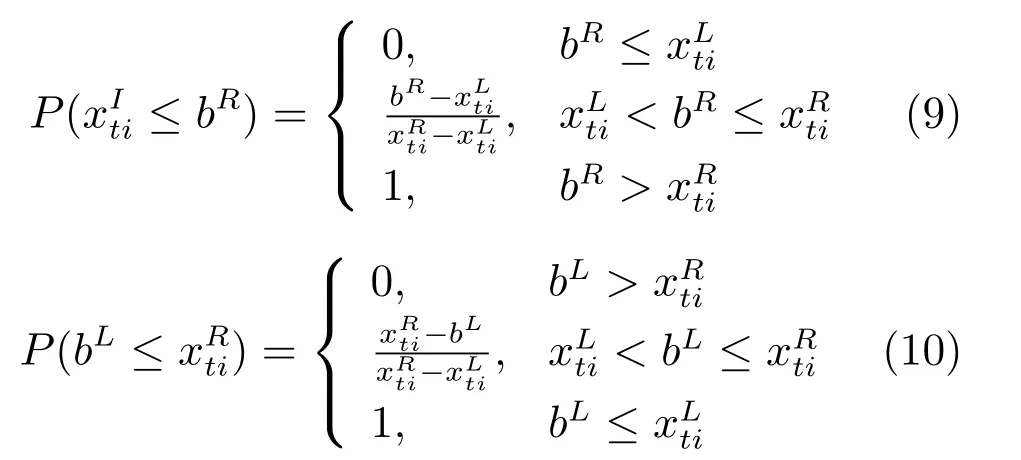
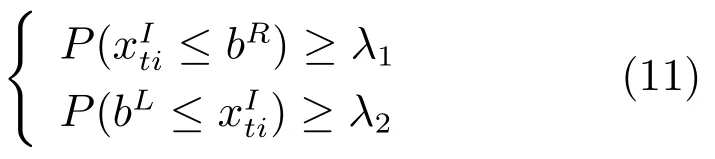
其中,0≤λ1,λ2≤1为预先给定的可能度水平,且λ1+λ2=1.实际应用中,约束可能度水平的选择与决策者的偏好相关.随着浸出率的增大,综合经济指标呈上升趋势,决策者选择较大的浸出率,则λ1<0.5,λ2>0.5;相反,浸出率的增大使得综合经济指标降低,决策者选择较小的浸出率,则λ1>0.5,λ2<0.5;当决策者无法判定综合经济指标与浸出率的变化趋势时,则λ1=0.5,λ2=0.5.

由前文描述公式可以看出湿法冶金工艺流程优化问题是具有复杂约束的优化问题.近年来一些智能优化算法被用来求解复杂优化问题[22−26],粒子群优化(Particle swarm optimization,PSO)算法作为一种新型演化算法,在很多情况下要比遗传算法等方法有效.然而基本的PSO算法容易陷入局部极值点问题,因此,本文将具有较强全局收敛性的二阶振荡PSO算法作为湿法冶金优化问题的求解算法[21,27].通过在粒子群优化算法中引入一个震荡环节,来改善算法的全局收敛性.

2.2.5 下游流程最优模态库建立

通过优化求解求得不同模态下的综合经济指标,根据下游综合经济指标得到最优操作策略(浸出率、置换率、氰化钠添加量、锌粉添加量等),从而建立最优模态库.最优模态库的表达形式如下所示:

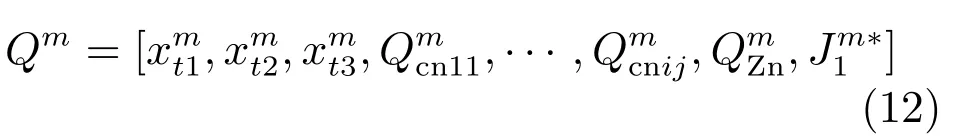
其中,m表示模态类型,即矿浆浓度5个状态[NB、NS、ZE、PS、PB];表示当前模态下工序级最优指标:一浸、二浸浸出率和置换率;分别表示当前模态下浸出过程和置换过程的最优操作变量(i=1,2;j=1,2,3);表示下游子流程综合经济指标,即在当前模态m下的最大经济效益.

2.3 湿法冶金过程优化模型求解

由于本文中所描述的湿法冶金全流程包含了上游调浆过程,在当前工况(放矿量)下,不同的调浆水对应的矿浆浓度不同,而对下游子流程的优化结果中可以看出不同的矿浆浓度会得到不同的综合经济指标.因此,在考虑调浆过程中调浆水经济效益后,对湿法冶金全流程建立全流程的优化模型.根据在不同工况(放矿量)下求得的综合经济指标,得到不同工况下的最优操作策略(浸出率、置换率、调浆水量、氰化钠添加量、锌粉添加量等),从而建立湿法冶金全流程最优模态库.

2.3.1 决策变量选取

对于调浆过程,调浆水量将直接决定调浆后的矿浆浓度,所以,全流程优化的决策变量选取为调浆过程的调浆水量、6个浸出槽的氰化钠添加量和置换过程的锌粉添加量.

2.3.2 目标函数

在全流程优化中,同样将单位时间每小时的经济效益最大作为优化目标.根据全流程工艺分析,全流程目标函数表示如下:

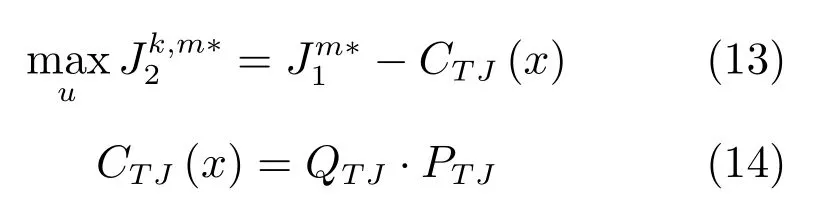
2.3.3 全流程最优模态库建立

在考虑调浆过程中调浆水经济效益后,通过优化求解求得不同工况下的全流程综合经济指标,建立全流程优化模式库,如表2所示.

根据在不同工况(放矿量)下求得的综合经济指标,通过全流程优化得到综合经济效益,同时得到不同工况下的最优操作策略(浸出率、置换率、调浆水量、氰化钠添加量、锌粉添加量等),则全流程最优操作模态库为:

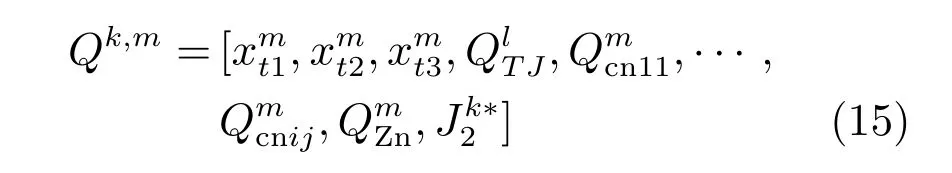
其中,k表示当前输入条件类型,即放矿量 5个状态 [NB、NS、ZE、PS、PB];l表示当前操作变量类型,即调浆水7个状态[NB、NM、NS、ZE、PS、PM、PB];表示全流程最佳工艺指标,即当前输入条件下的最优经济效益.

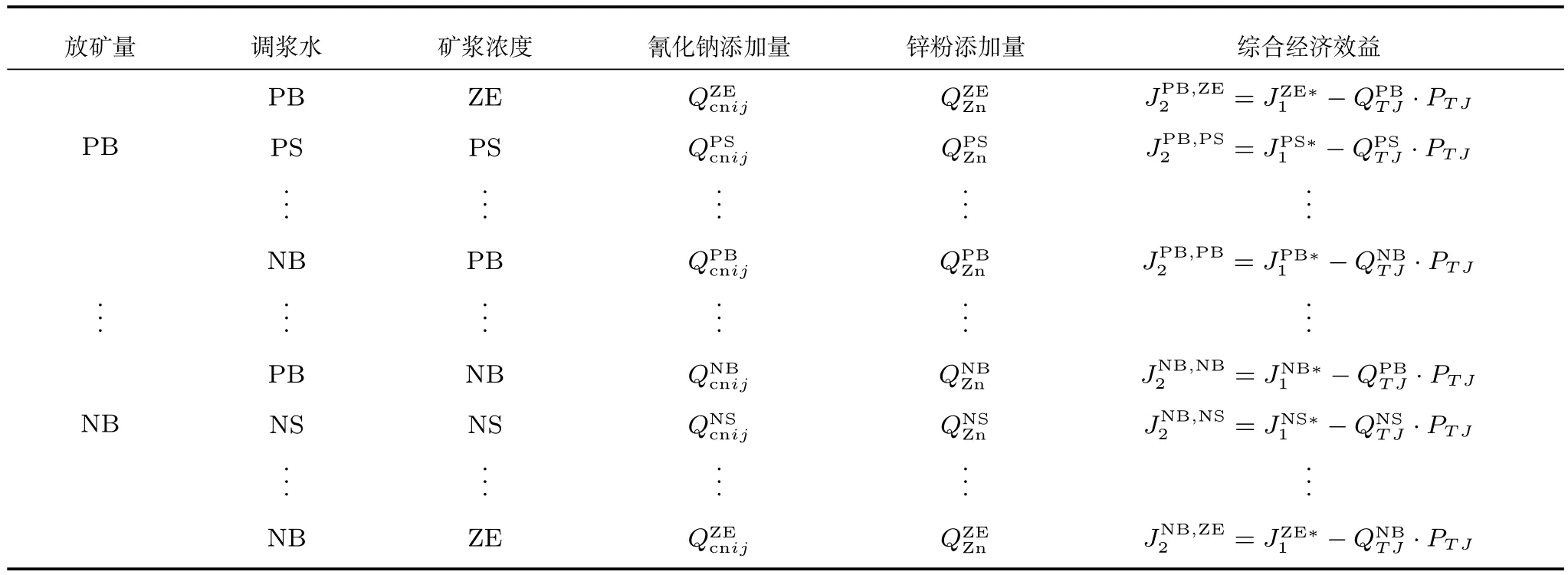
表2 全流程优化模式库Table 2 Plant-wide optimization pattern base

基于区间数的湿法冶金过程分层优化方法的实现流程如图7所示.具体步骤如下:

步骤1.结合专家知识对无法建立定量模型子流程建立定性知识模型,并将输出变量划分模态.

步骤2.针对定性模型输出变量每一模态,利用区间数的优化方法对下游子流程优化求解,通过求解式(6)∼(8)获得下游子流程的综合经济指标和最优操作参数Qcnij(i=1,2;j=1,2,3),QZn,并建立最优模式库.

步骤3.在下游最优模式库基础上对全流程优化操作,获得当前输入条件下的最优操作模态库.

3 仿真及分析

由第2节可知,湿法冶金过程优化包括两个部分:1)下游基于区间数的分层优化;2)在下游优化结果的基础上对湿法冶金全流程优化.

3.1 下游区间优化结果分析

对无法建立定量模型的调浆过程,通过建立定性知识模型得到输出变量矿浆浓度5个定性值,分别为负大 (NB)、负小 (NS)、零 (ZE)、正小 (PS)、正大(PB),针对这5种模态类型,分别通过基于区间数的分层优化方法求解各个模态中的综合经济指标和最优操作变量,进而建立下游子流程的最优模式库,优化模型中其他的相关变量及参数值见表3.

采用二阶振荡PSO算法求解下游子流程优化问题,由于外层和内层都需要优化求解,所以算法的参数设置内外层分别为:1)外层优化:种群规模为100;最大迭代次数为40;惯性权重为0.8;学习因子c1和c2分别为1.2和0.9.2)内层优化:种群规模为10;最大迭代次数为40;惯性权重为0.9;学习因子c1和c2分别为0.95和0.95.区间约束可能度水平λj1=0.5,λj2=0.5.通过下游子流程优化,优化结果如图8所示,并建立了最优模式库如表4所示.

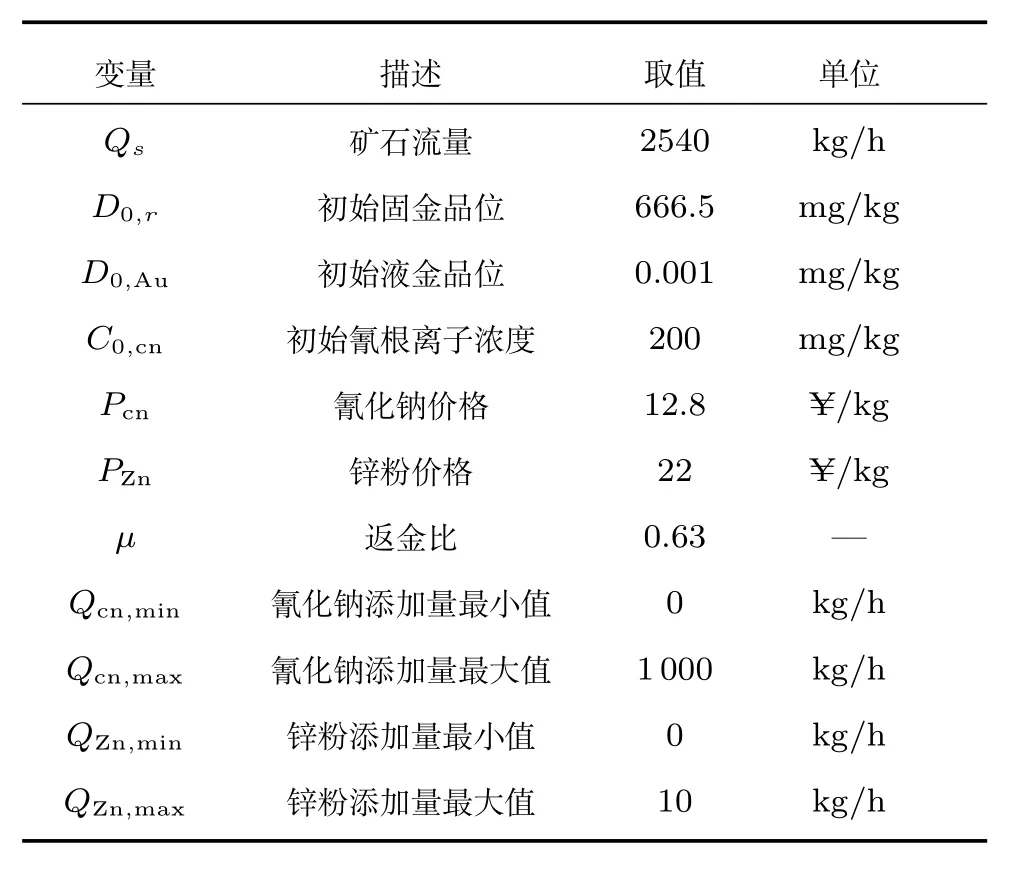
表3 模型过程变量及相关参数取值Table 3 Values of process variables in mechanistic model and relevant parameters

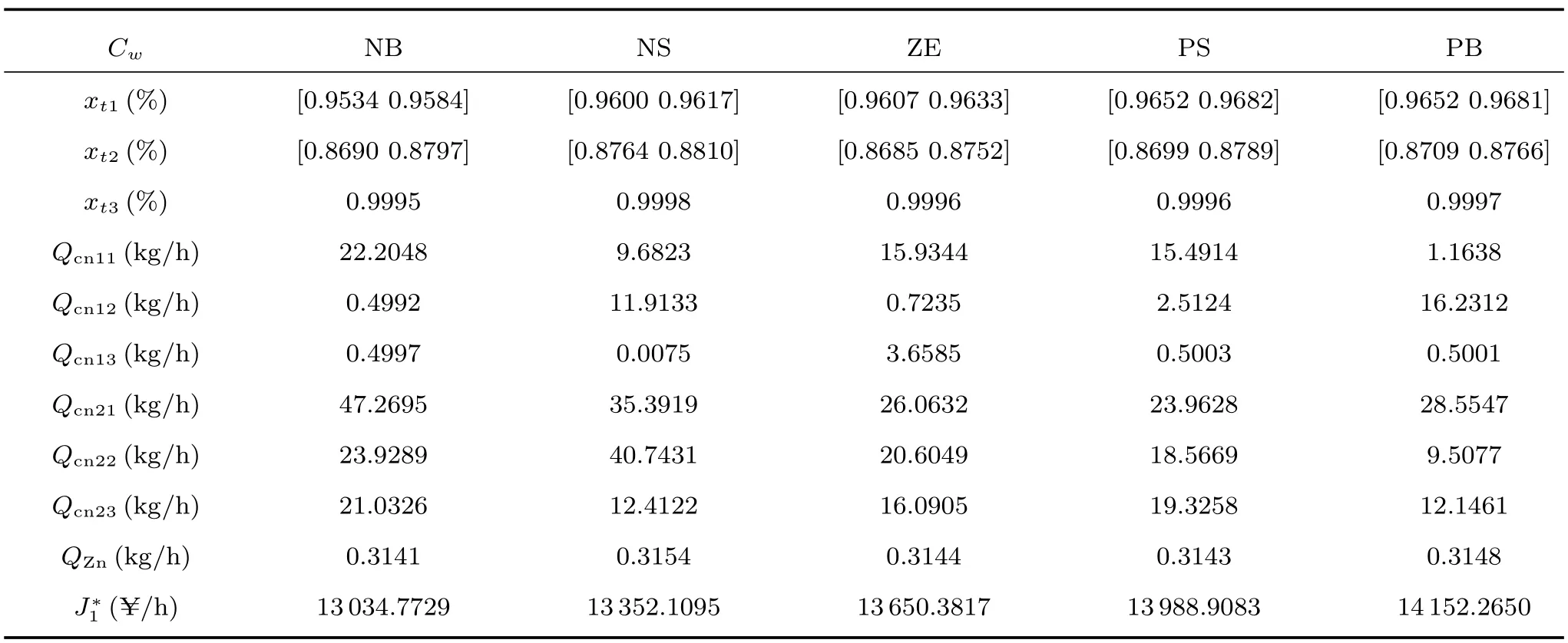
表4 优化结果最优模式库Table 4 Results of the optimal-pattern base

在湿法冶金实际生产过程操作范围内,根据矿浆浓度的5种模态类型(负大(NBCw)、负小(NSCw)、零(ZECw)、正小(PSCw)、正大(PBCw)),通过式(6)分别求得不同模态下一浸、二浸和置换工序过程中的最小物耗区间值xIci,min(i=1,2,3)和各个工序的质量指标xti(i=1,2,3),从而求出经济指标.由图8(a)可以看出,随着模态等级的提高,工序级优化的经济指标呈上升趋势.对于过程级优化,在满足工序级优化结果的基础上,通过式(7)求得一次浸出和二次浸出过程中各个浸出槽的最优氰化钠添加量,如图8(c)和(d).从图中可以得出,随着矿浆浓度模态等级的提高,一次浸出物耗和二次浸出物耗呈下降趋势.最后,根据分层优化结果,通过式(1)∼(3)求得下游流程的综合经济效益,从图8(b)中可以看出,不同矿浆浓度模态下的综合经济指标随着模态等级的提高呈上升趋势.从图8中可以看出,矿浆浓度的模态转换,会导致综合经济效益和决策变量优化值的变化.但矿浆浓度的小范围波动并不会造成模态的变化,即矿浆浓度的模态转换并不是频繁发生的,因此优化指标和控制变量也并不会频繁变化.

图7 基于区间数的湿法冶金过程分层优化流程图Fig.7 Flow chart of the process hierarchical optimization method based on interval number for hydrometallurgy

为了证明本文提出的基于区间数的分层优化方法的优越性,这里假定矿浆浓度模态等级为NB(负大),矿浆浓度参数设定值为0.3(g/g),实际现场矿浆浓度离线化验值为0.33(g/g).

将本文提出方法与传统采用矿浆浓度固定参数值的分层优化方法和全流程优化方法相比较,实验结果如图9所示.图9(a)中第一条曲线表示矿浆浓度为0.33(g/g)时,通过全流程优化得到最优操作参数后带入全流程模拟模型中得到的综合经济效益;同样,第二条与第三条曲线分别表示矿浆浓度为0.3(g/g)时,通过全流程优化与分层优化得到最优操作参数后带入全流程模拟模型中得到的综合经济效益,此时全流程模拟模型中的矿浆浓度为0.33(g/g).

图9(a)说明,由于模型中存在参数不确定性,分层优化与全流程优化方法中的矿浆浓度采用定值0.3(g/g)计算,其优化结果不是模拟的实际过程最优设定点.将优化出的结果带入全流程模拟模型中后,由于实际现场中矿浆浓度为0.33(g/g),两种方法得到的模拟结果均未达到实际过程的综合经济效益.而本文提出的区间分层优化方法,通过将不确定参数值定义为区间值,采用基于区间数的分层优化方法,其结果与传统方法相比较,本文方法能够有效解决模型存在不确定性问题,结果如图9(b)所示.

对于基于区间数的优化,从式(11)中可以看出不同的区间约束可能度水平λ1与λ2将得到不同的优化结果,由于λ1+λ2=1,所以这里只考虑一种约束可能度水平λ2情况下的优化.下面具体从10种不同的约束可能度水平λ2对问题进行优化,优化结果如图10所示.

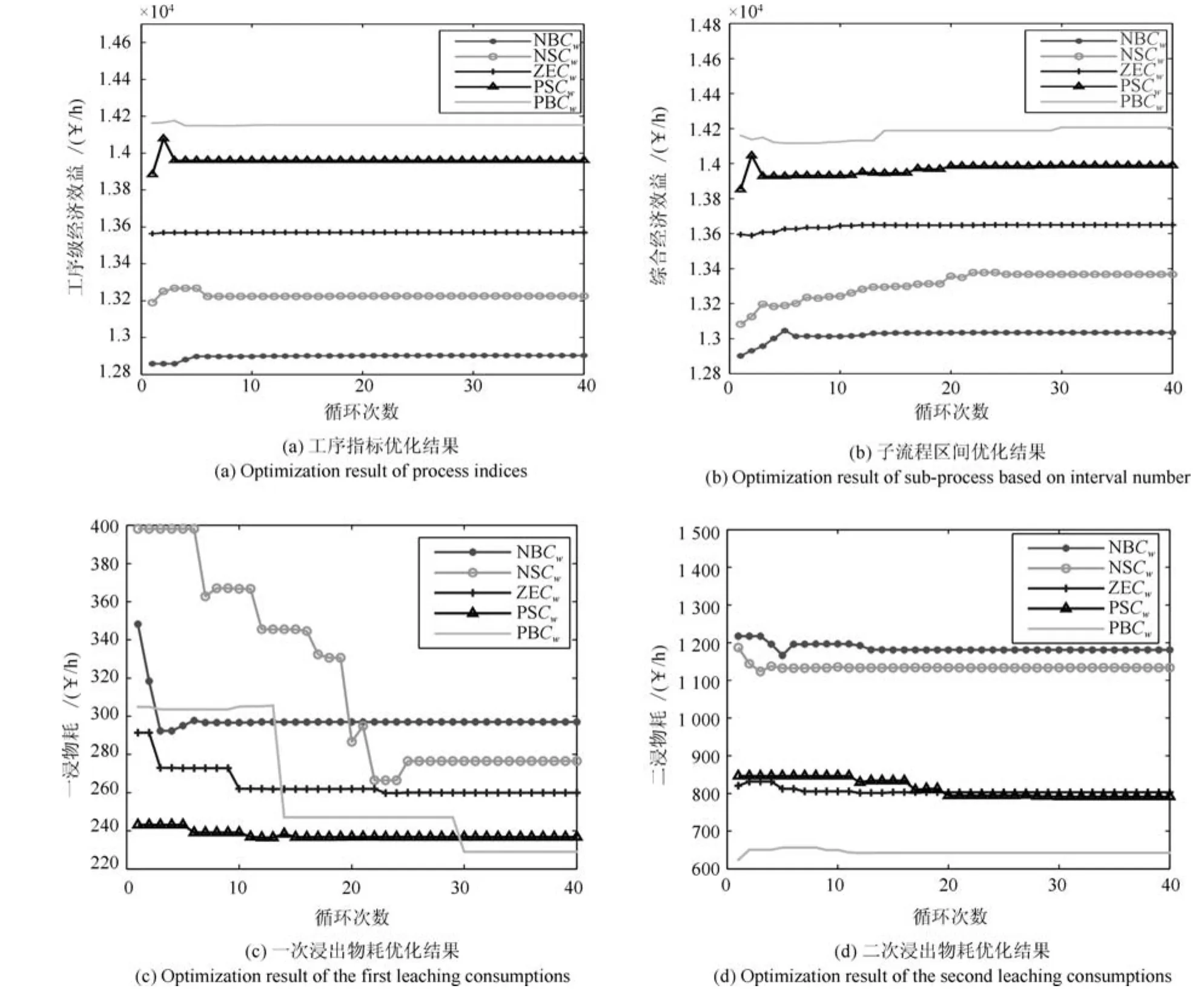
图8 基于区间数的分层优化结果Fig.8 Results of the hierarchical optimization method based on interval number

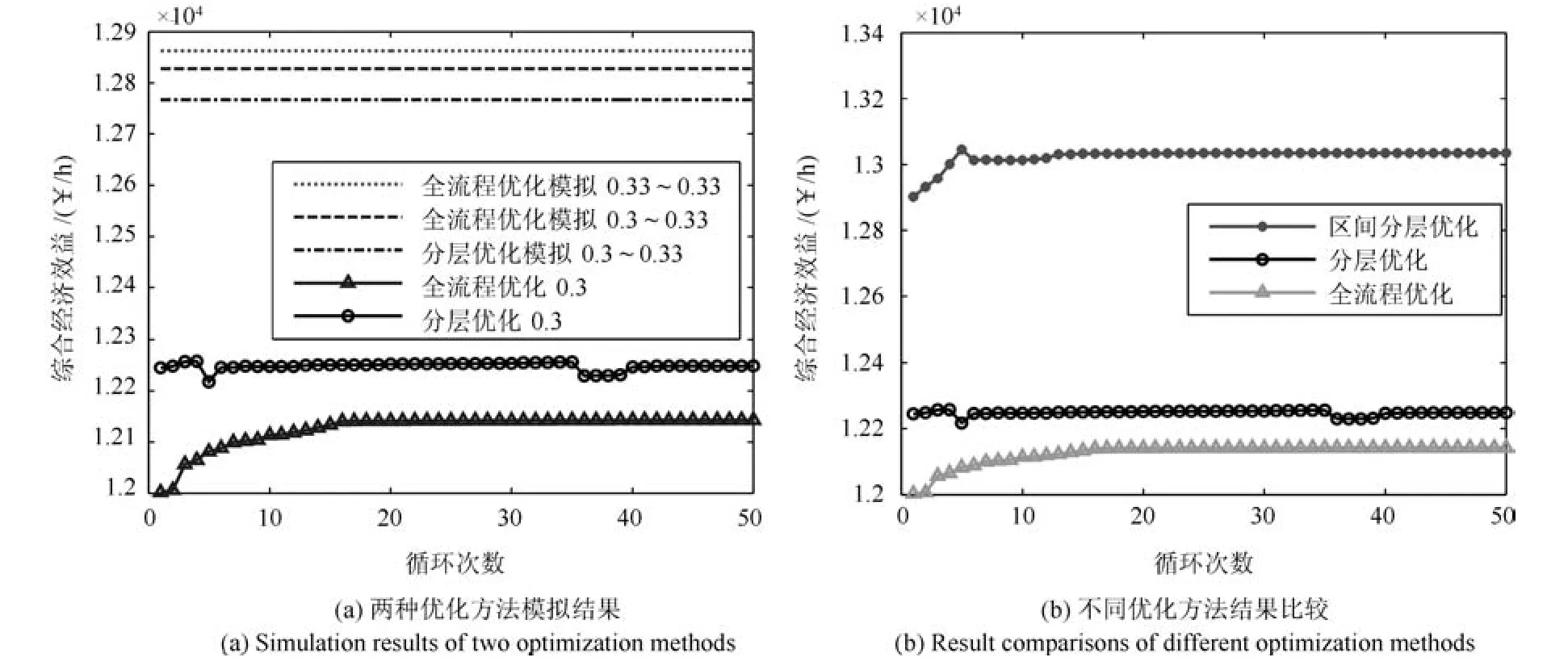
图9 不同优化方法的性能比较Fig.9 Performance comparisons of different optimization methods

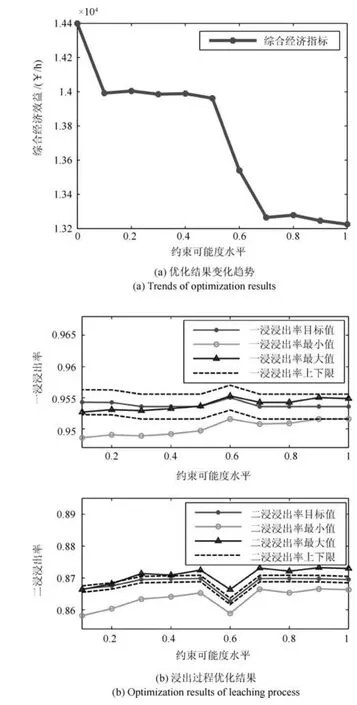
图10 不同约束可能度水平下的优化结果Fig.10 Results of the different constraints possibility degree levels

图10(a)说明,随着约束可能度水平λ2的提高,综合经济指标呈下降趋势.这是因为较小的约束可能度水平使得转化后的确定性优化问题式(11)的可行域变大,从而可获得更优的目标性能,即较大的综合经济指标.在图10(b)中,通过过程级优化后的浸出率,随着约束可能度水平的提高,逐渐趋向于通过工序级优化的浸出率指标范围内.由于二浸浸出率的指标范围更加严格,从图中可以看出过程级优化后的浸出率均落在目标范围外,但随着约束可能水平的调高,浸出率逐渐向目标逼近.

为了进一步说明不同约束可能度水平λ2下的优化结果,通过对过程级优化模型分析,得到一浸浸出率和二浸浸出率的惩罚函数,结果如图11所示.从图中可以看出,随着约束可能度水平λ2的提高,相应的一浸惩罚逐渐趋向于0,二浸惩罚由于前面提到目标范围约束严格,虽然没有逐渐递减为0,但整体呈下降趋势.

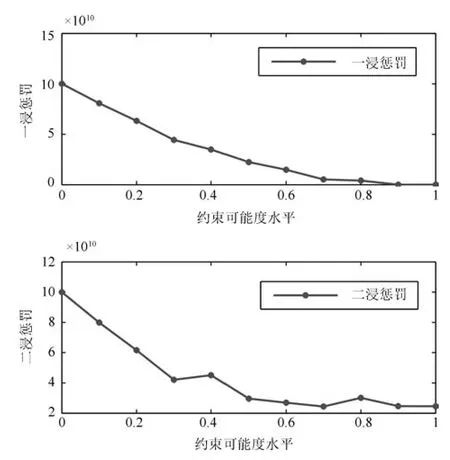
图11 不同约束可能度水平下的惩罚结果Fig.11 Results of penalties under different constraints possibility degree levels

3.2 下游区间优化结果分析

通过下游子流程优化得到各个模态的最优经济指标和操作变量,根据当前放矿量输入状态,对当前工况实现全流程优化,并建立全流程的优化操作模态库,如表5所示.从表中可以看出,调浆工艺过程中,根据当前不同的放矿量输入条件,调浆水的调节量与矿浆浓度的模态等级在合理匹配情况下,能够在下游经济效益最优的基础上,使得当前工况下的全流程生产过程经济指标达到最大.这样在当前工况条件下,通过查找全流程优化操作模态库中与当前工况相对应的操作变量,应用到实际生产过程中,将得到最优的经济指标,满足湿法冶金全流程最优控制.

4 结论

本文分析了湿法冶金生产过程的特点及其建模优化中存在的难点,研究了基于区间数的过程分层优化方法.针对存在无法定量建模环节的复杂工业流程,提出了湿法冶金过程建模优化的框架.通过将定性模型与定量模型相结合,提出了湿法冶金过程优化方法.针对工业流程下游子过程中存在无法确定的区间变量,采用区间优化方法实现了下游流程的优化.将所提方法应用于湿法冶金生产过程中,仿真结果证明了建模与优化方法的有效性.

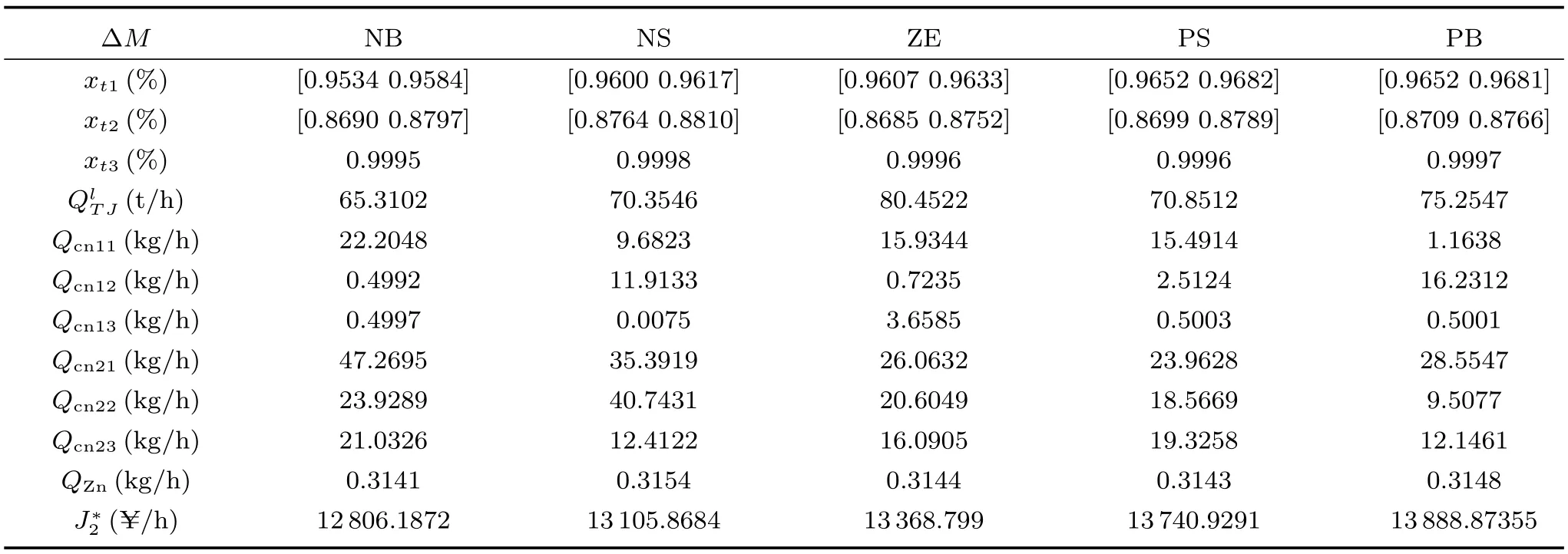
表5 全流程优化结果Table 5 Results of plant-wide optimization